空间四自由度柔顺并联机构设计与仿真

高新宇,张士军,孟繁勋,杨 璐

(1.山东建筑大学机电工程学院,山东 济南 250100)(2.山东农业大学经济管理学院,山东 泰安 271000)

随着人类社会的进步和科学技术的飞速发展,人们在超精密加工、纳米技术、精密测量、生物医学等领域的研究越来越深入,精密定位技术在这些领域都有非常广泛的应用[1]。

柔性并联机构促进了精密定位平台的发展,将柔性铰链理论和并联机构结构特性相结合,应用柔性铰链替换法就能够得到相应的柔性并联机构[2]。与传统的并联机构相比,柔性并联机构具有各支链的运动副都可用柔性铰链代替的特点[3]。压电驱动具有更高的灵敏度、更快的反应速度和更大的输出力,所以一般的微位移平台会选择压电驱动作为驱动方式[4]。压电陶瓷具有分辨率高、能耗较低、体积较小且没有电磁干扰等优点,所以压电陶瓷用作微位移驱动器更适合[5]。

现阶段,平面多自由度精密定位平台的发展非常迅速,例如陈庭辉[6]对传统的平面微位移平台进行了优化设计,并且改进了放大机构,提高了定位精度。现有的研究很少在空间微位移平台领域展开。本文设计的微位移运动平台使用空间多自由度平台的设计方法,采用柔性铰链代替传统的运动副,将传统的空间并联机构改进为空间柔性并联机构,消除了传统机构铰链配合的摩擦与间隙,可以实现4种运动。

1 柔性铰链

和传统的运动副相比,柔性铰链具有突出的优势,包括结构相对简单、没有运动摩擦和间隙、能够克服由于惯性引起的振动等,柔性铰链的缺点主要是运动的行程较小,所以常用于微动领域以提高机构精度。目前,柔性铰链广泛应用于精密定位平台等领域[7]。

本文选用的柔性铰链有如下4种:柔性球副、柔性转动副、柔性移动副、柔性虎克铰。

1)柔性球副。吴石磊[8]针对不同类型柔性球副进行了力学建模以及理论计算和仿真。柔性球副具有3个自由度,可以在3个方向做独立运动,本文选用椭圆型柔性球副,如图1所示。

图1 柔性球副

2)柔性转动副。张忠奎、陈航[9-10]对转动副的转角刚度进行了研究,得出柔性转动副的中间部分在力或力矩的作用下非常容易变形,此种变形为可逆弹性变形,可实现绕转动轴的转动,柔性转动副具有1个自由度。本文选用图2所示的圆弧型柔性转动副。

3)柔性移动副。杨春辉[11]对直梁平行板型柔性移动副进行了深入研究,该柔性移动副采用对称结构,不仅可以实现较大范围内的运动且具有更高的精度。本文选用图3所示的直梁平行板型柔性移动副,它具有1个自由度。

图3 柔性移动副

4)柔性虎克铰。孙炜等[12]在给定参数的情况下对3种柔性虎克铰进行了理论计算和有限元分析,对比了输出行程和转动特性,为柔性虎克铰的选择提供了帮助。本文选用图4所示的柔性虎克铰,其可进行两个方向的相互转动,具有2个自由度。

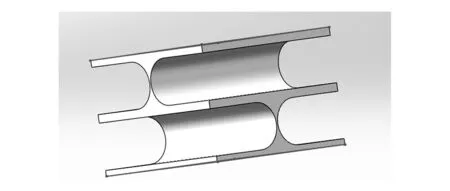
图4 柔性虎克铰

2 空间四自由度定位平台设计

2.1 空间四自由度并联机构简图

本文提出一种空间四自由度并联机构,其简图如图5所示。图中,动平台由a、b两部分构成,a和b之间由转动副11相连接。1、4、7、13、16、19为移动副,2和5为万向铰,3和6为球副,8、9、10、12、14、15、17、18为转动副。

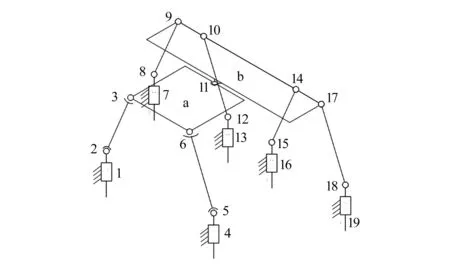
图5 空间四自由度并联机构

2.2 空间四自由度并联机构自由度计算

图5中构件1～6在一个平面上,构件7～19在一个平面上,可以把机构分为a和b两部分来计算自由度。先计算b部分的自由度Fb:

Fb=3n-2Pl-Ph

(1)

式中:n为构件数,Pl为低副数目,Ph为高副数目。其中,n=9,Pl=12,分别是4个移动副和8个转动副,可得Fb=3×9-2×12=3,a部分一共有5个构件,这5个构件分别有6个自由度,移动副1和4分别约束5个自由度,而万向铰2和5分别约束4个自由度,球副3和6分别约束3个自由度,可得a部分的自由度Fa等于6。由此得出该机构的自由度F=Fa+Fb-5=4,即该空间四自由度并联机构具有4个自由度。

2.3 空间四自由度柔顺并联定位平台设计

本文设计的空间四自由度柔顺并联定位平台由图5所示的空间四自由度并联机构采用刚体替换法得到,运动支链上用柔性铰链代替传统的运动副。空间四自由度柔顺并联定位平台如图6所示。

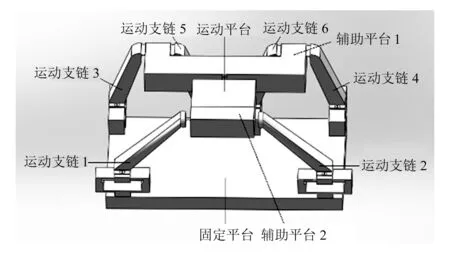
图6 空间四自由度柔顺并联定位平台

3 定位平台运动学建模

3.1 定位平台位姿分析

根据机械原理的知识,平台沿X、Y轴平移以及绕Z轴转动时,运动平台和辅助平台做同步且相同的运动,所以这3种运动可以看做是在同一个平面内的运动,故可以将这3种运动简化成平面运动。图7为微位移平台沿Y轴平移的运动简图,由于6条支链运动是同步的,取P点和A点分析,当P点和A点输入相同的位移时,E和F两点也有相同的输出位移。

图7 沿Y轴平移运动简图

3.2 定位平台运动学逆解分析

3.2.1沿X轴平移

首先建立定位平台的几何模型,沿X轴平移运动简图如图8所示。

图8 沿X轴平移运动简图

执行器的输出位移γ=[xP,yP,φP],输入位移di=[d1,d2,d3,d4,d5,d6],XOY为静坐标系,静坐标系原点O位于整个平台的中心处,X′PY′是固定在动平台中心的动坐标系,(xP,yP)为动平台动坐标系X′PY′原点P的坐标,φP为动平台绕Z轴的转动角,d1,d2,…,d6为6条运动支链对空间四自由度柔顺并联定位平台的输入量。动平台的顶点为6个铰接点J1,J2,…,J6;Hi和Ji分别代表相应的转动关节;γi为每个压电陶瓷驱动器的输出位移,与X轴正向的夹角为αi;βi为X轴正向与刚性连杆HiJi的夹角,i=1,2,…,6。

对定位平台进行运动学逆解分析,即通过末端执行器的输出位移γ来求解输入位移di。基于几何方法,由四自由度柔顺并联机构闭链约束可得约束方程为:

lOP+lPJi=lOGi+lGiHi+lHiJi

(2)

式中:lOP为O点到P点的距离,lPJi为P点到Ji点的距离,lOGi为O点到Gi点的距离,lGiHi为Gi点到Hi点的距离,lHiJi为连杆HiJi的长度。

由式(2)和图8可得:

di)cosαi+lHiJicosβi

(3)

di)sinαi+lHiJisinβi

(4)

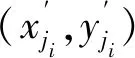
当定位平台沿X轴平移时,动坐标系在Y方向不发生偏移且不发生旋转,得出φP=0,yP=0,而压电陶瓷输出位移是竖直方向,即αi=0。简化式(3)、(4)得:

(5)

(6)

整理式(5)、(6),消去中间变量βi得:

(7)

3.2.2绕Z轴转动

对绕Z轴的转动进行分析时,方法同绕X轴平移。先建立该运动下定位平台的几何模型,运动简图如图9所示。

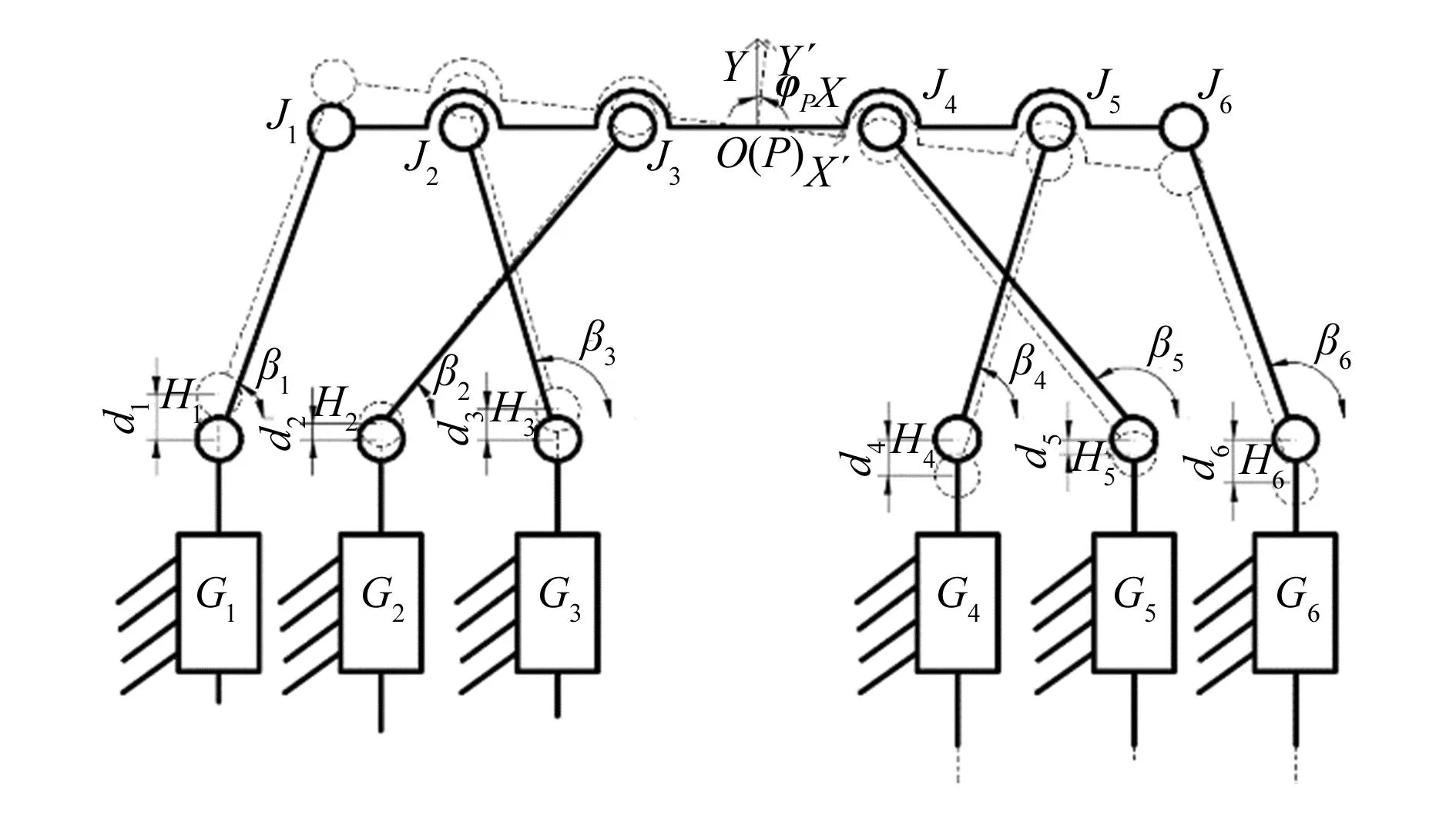
图9 沿Z轴转动运动简图

基于几何方法,由式(2)和图9可得式(3)、(4),当定位平台绕Z轴旋转时,动坐标系在Y方向不发生偏移,得出yP=0,压电陶瓷输出位移依旧是竖直方向,即αi=0,简化式(3)、(4)得:

(8)

(9)

整理式(8)、(9),消去中间变量βi得:

(10)

3.2.3绕X轴转动

首先,建立定位平台的几何模型,绕X轴转动运动简图如图10所示。

图10 绕X轴转动运动简图

分析方式同3.2.1和3.2.2,此时只有运动支链1和2运动,其余支链不动。末端执行器的输出位移η=[xP,yP,φP],输入位移di=[d1,d2]。动平台的顶点为2个铰接点J1和J2;ηi为每个压电陶瓷驱动器的输出位移。

基于几何方法可得:

(11)

由四自由度柔顺并联机构闭链约束可得约束方程为:

lOP+lPJi=lOGi+lGiHi+lHiJi

(12)

由式(12)和图10得:

(13)

(14)

当定位平台绕X轴转动时,压电陶瓷输出位移是竖直方向,即αi=0,将式(11)代入并简化式(13)、(14)得:

(15)

(16)

整理式(15)、(16),消去中间变量βi得:

(17)

4 定位平台有限元仿真分析

由前文可知,本文设计的空间四自由度柔顺并联定位平台有4个自由度,能够实现4种不同的运动,即2种转动和2种移动。利用SolidWorks软件建立空间四自由度柔顺并联定位平台模型,将其导入ANSYS Workbench软件中进行有限元分析,从而得出4种不同情况下的位移,即该定位平台所能实现的运动[13]。其中,压电陶瓷pst150/5/100 vs10的行程为0～0.01 mm,定位平台材料选用65Mn弹簧钢,密度ρ=7.81 g/cm3,弹性模量E=2.1×1011Pa,泊松比μ=0.288。

4.1 沿Y轴平移

当6条运动支链处输入端的输入位移均为10 μm时,根据机械原理分析该机构的运动可知,动平台输出位移应为10 μm,图11为有限元分析结果,理论计算结果和仿真结果的最大误差为0.15%。

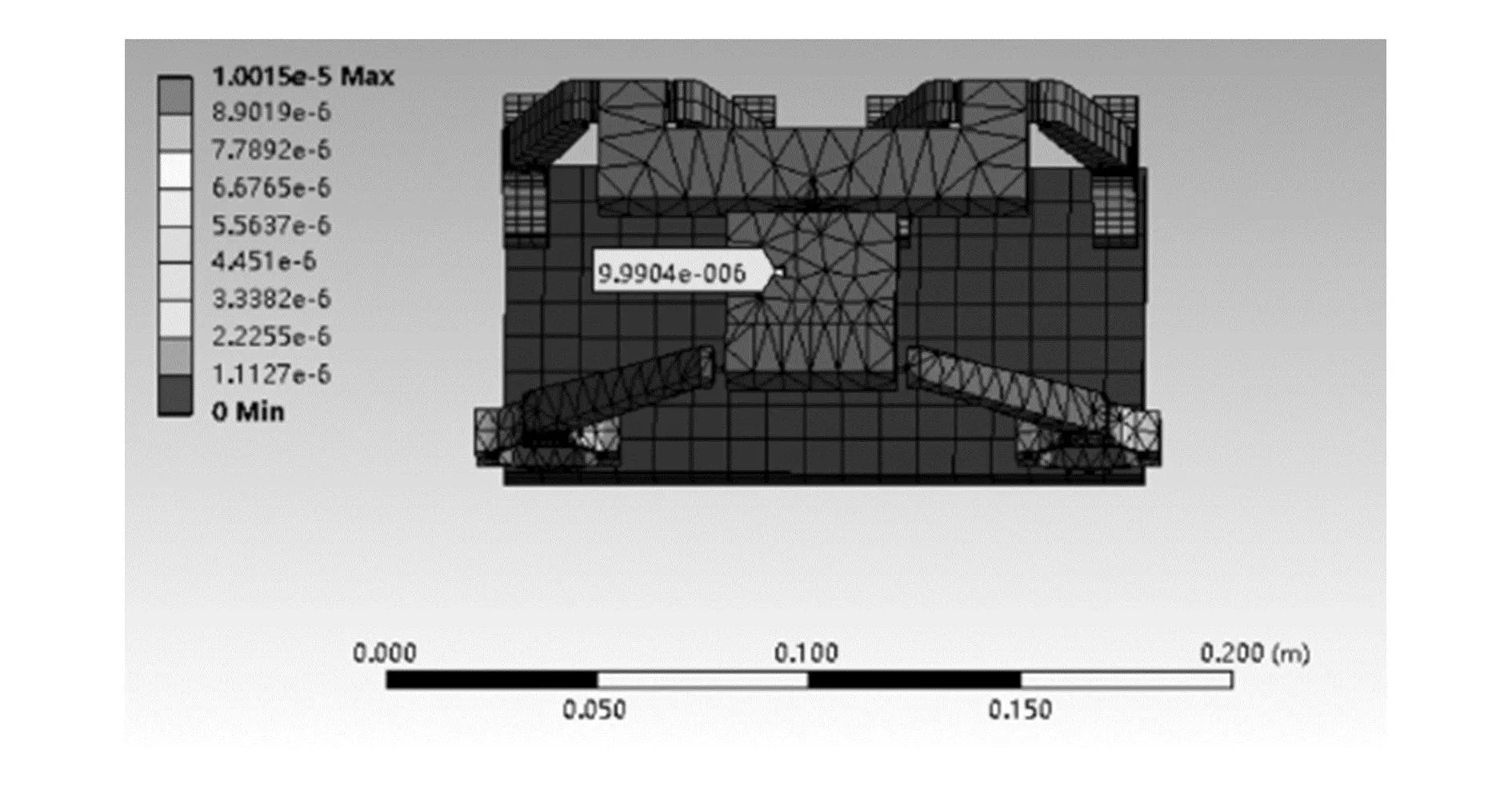
图11 沿Y轴平移位移云图

4.2 沿X轴平移

当6条运动支链处输入端的输入位移分别为10.000、-10.000、4.142、-4.142、-4.142、4.142 μm时,由式(7)得动平台输出位移为11.071 μm,有限元分析的结果如图12所示,理论计算结果和仿真结果的最大误差为10.112%。

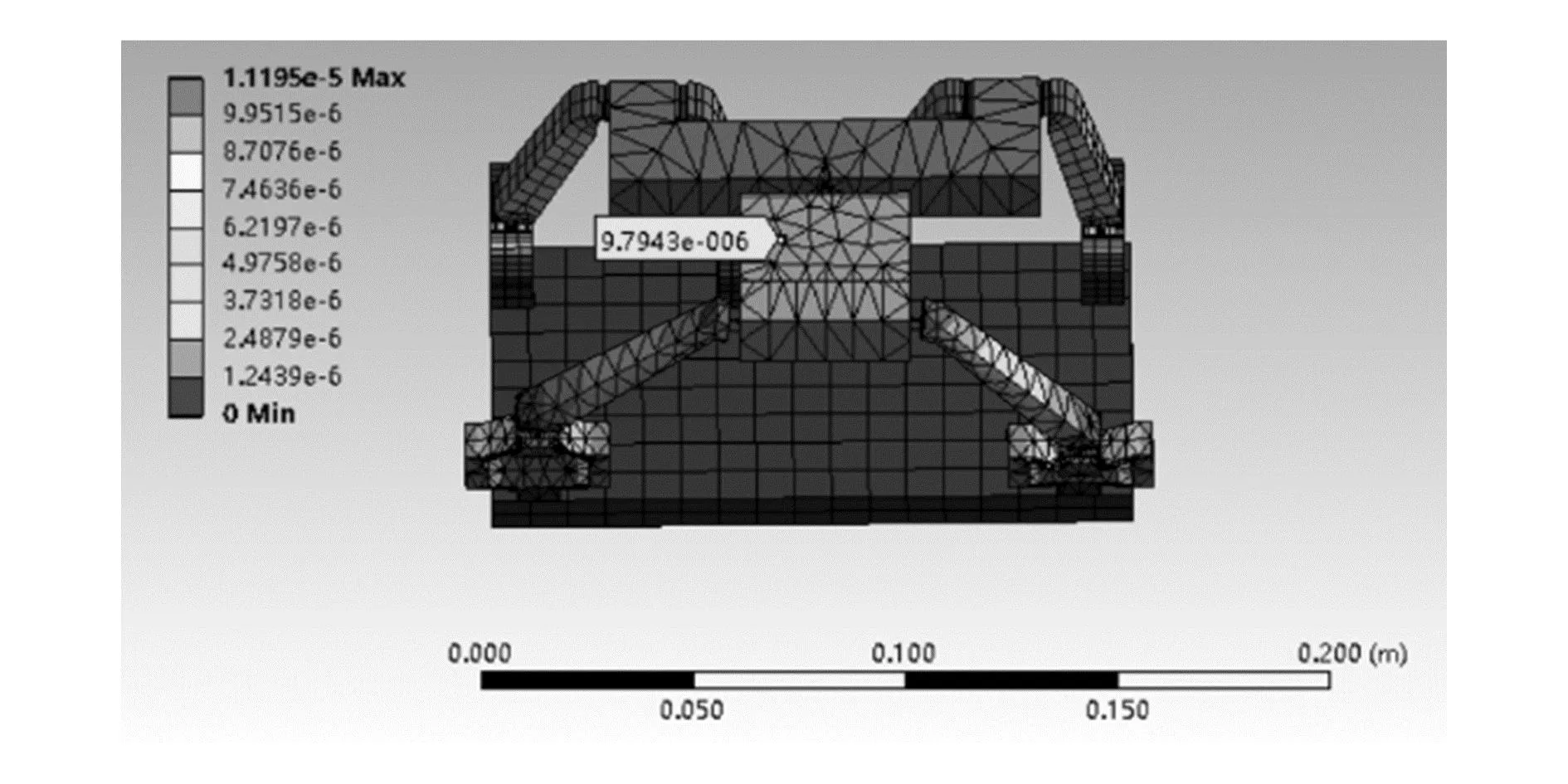
图12 沿X轴平移位移云图

4.3 绕Z轴转动

由图13及式(10)得,当6条运动支链处输入端的输出位移分别为4.013、-4.013、10.000、-10.000、6.265、-6.265 μm时,φP范围为0～0.053 74°。

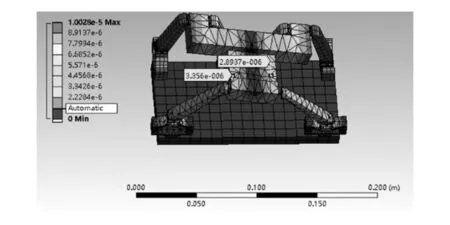
图13 绕Z轴转动位移云图

4.4 绕X轴转动

由图14和式(17)得,当6条运动支链处输入端的输出位移分别为10、-10、0、0、0、0 μm时,φP范围为0～0.042 32°。

图14 绕X轴转动位移云图

5 结果分析

由前文可知,沿Y轴平移和沿X轴平移时最大相对误差为0.150%和10.112%,绕Z轴转动和绕X轴转动时最大相对误差为5.040%和9.580%,计算可得,误差均在合理范围内,验证了运动学模型理论分析的合理性。

6 结束语

本文设计了一种空间四自由度柔顺并联机构。使用SolidWorks软件建立了空间四自由度柔顺并联定位平台的模型,首先了进行理论计算,然后用ANSYS Workbench软件进行了有限元分析,得到位移云图。经分析可知,驱动平台运动时其位移分布较合理,误差也在合理范围内。空间四自由度柔顺并联定位平台定位精度可达微米级。