论相似三角形在实际生活中的应用

赵芳

［摘 要］相似三角形在实际生活中的应用在中考数学中常有涉及，对学生的能力要求较高。文章结合几个典型例题，从五个方面探讨相似三角形在实际生活中的应用，旨在帮助学生理解相似三角形的概念，培养学生的应用能力与数学素养。

［关键词］相似三角形；实际生活；初中数学

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）29-0013-03

相似三角形是初中数学的重要内容，在现实生活中具有广泛的应用。利用相似三角形，可以进行方案设计，可以求矩形的最大面积、楼高、桥长等。学生掌握相似三角形在实际生活中的应用，可以更好地理解相似三角形的概念，培养应用能力与数学素养。本文结合几个典型例题，从五个方面探讨相似三角形在实际生活中的应用，以提高学生解决实际问题的能力，培养学生的思维品质。

一、利用相似三角形进行方案设计

利用相似三角形的性质与判定测量物高或物宽，其可行的方案有多种，有的选择“A字型”相似，有的选择“X型”相似，有的选择锐角三角形，有的选择直角三角形，有的选择简单的方案，有的选择复杂的方案。选择的图形与方案决定了解决问题的复杂程度，也影响了测量的精度，所以应尽量采用易操作、误差较小的实施方案。

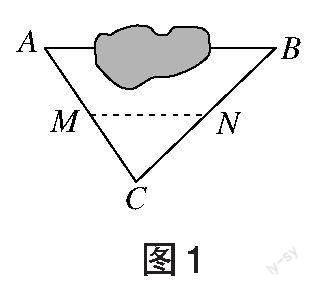
［例1］如图1所示，A、B两点被池塘隔开，为测量AB两点的距离，在AB外选一点C，连接AC和BC，并分别找出AC和BC的中点M、N，则MN是[△ABC]的中位线，根据三角形的中位线定理，三角形的中位线平行于第三边且等于第三边的一半。如果测得[MN=20 m]，那么[AB=2×20 m=40 m]。（1）小红说：测AB距离也可以如图2所示用三角形全等知识来解决。请根据题意填空：延长AC到D，使[CD=]               ，延长BC到E，使[CE=]                ，由全等三角形得[AB=ED]；（2）小华说：测AB距离也可以由三角形相似的知识来设计测量方法，求出AB的长。请根据题意在图3中画出相应的测量图形：延长AC到H，使[CH=2AC]，延长BC到Q，使[CQ=2BC]，连接QH，若测得QH的长是400米，你能测出AB的长吗？若能，请测出；若不能，请说明理由。

解：（1）在[△ABC]与[△DEC]中，有对顶角[∠ACB=∠DCE]，延长AC到D，使[CD=AC]，延長[BC]到[E]，使[CE=BC]，根据两边及其夹角分别对应相等的两个三角形全等，得[△ABC ]≌[△DEC]，根据全等三角形对应边相等，得[AB=ED]。

点评：本题采用三种不同的方法测量池塘的宽度，第一种方法是利用三角形的中位线，第二种方法是利用全等三角形，第三种方法是利用相似三角形，展现了数学知识在解决实际问题中的价值。实际上，采用相似三角形测量池塘宽的方法也不止一种，可以采用“A字型”相似、“斜A字型”相似，也可采用“X型”相似、“斜X型”相似等。

二、利用相似三角形求矩形的最大面积

当一个矩形的四个顶点都在三角形的边上时，我们称这样的矩形为三角形的内接矩形。形状与大小一定的三角形，当矩形的宽为多少时，它的内接矩形面积最大呢？这是一个有趣的话题。当矩形内接于三角形时，存在相似三角形，利用相似三角形对应高的比等于相似比及矩形的面积公式，建立关于矩形的宽的二次函数，利用二次函数的最值可以求得矩形的最大面积。

（10-x）]∶10，∴[DE=10-x]，∴矩形DEFG的面积=[DE·DG=（10-x）·x=-（x-5）2+25]，∴当[x=5]时，矩形DEFG的面积最大。

（3）如图9所示，延长BA、CD交于O，作[DH⊥AO]交[AO]于点H，∵[∠B=∠C=60°]，∴[△OBC]是等边三角形，∴[OB=OC=

点评：本题考查了相似三角形与二次函数的应用，利用相似三角形对应高的比等于相似比，可求得矩形另一边的表达式。求面积最值时一般应用二次函数的最值性质。在上述的探究中发现，对于不规则图形的面积，通常可分割或添补成规则图形的面积进行求解。

三、利用相似三角形求楼高

利用相似三角形求楼高，就是测试者与大楼之间放一面镜子，测试者在地面来回走动，当在镜子中看到大楼顶端的像时，由于反射角等于入射角，得到一组相似三角形，利用相似三角形对应边成比例，即可求得大楼的高。

［例3］在阳光明媚的周末，小明和小芳一起去登凤凰山，在山顶，他们想用一些测量工具和所学知识测量“凤凰楼”的高度。他们经过观察发现，观测点与“凤凰楼”底部间的距离不易测得，因此他们运用以下方法来进行测量：如图10所示，小芳在小明和“凤凰楼”之间的直线BM上放一平面镜，在镜面上做一个标记，这个标记在直线BM上对应位置为点C，镜子不动，小明看着镜面上的标记来回走动，走到点D时，看到“凤凰楼”顶端点[A]在镜面中的像与镜面上的标记重合，这时，测得小明眼睛与地面的高度[ED=1.5]米，[CD=2]米，然后，小明从点D沿DM方向走了24米，到达“凤凰楼”影子的末端F处，此时，测得小明身高FG的影长[FH=3.3]米，[FG=1.65]米。已知[AB⊥BM]，[ED⊥BM]，[GF⊥BM]，其中，测量时所使用的平面镜厚度忽略不计。请你根据题中提供的相关信息，求出“凤凰楼”的高AB的长度。

点评：此题如果观测点与“凤凰楼”底部间的距离可以测得，即已知[BC]的长，只用一组相似三角形即可求凤凰楼的高，但观测点与凤凰楼底部间的距离不易测得，所以用两组相似三角形建立方程组求楼高，体现了相似三角形在解决问题中的价值。

四、利用相似三角形求桥长

利用相似三角形求桥长，也就是在桥的位置建立相似三角形的模型，利用相似三角形对应边成比例求得对应边的长，即桥长。这里既可以建立“A字型”相似，也可以建立“X型”相似。在下面的例题中，既利用了“A字型”相似三角形，也利用了“X型”相似三角形，不过建立“X型”相似时，需要作一条辅助线。

［例4］某市为了加快城乡发展，保障市民出行方便，在流经该市的河流上架起一座桥，连通南北，铺就城市繁荣之路。小明和小颖想根据自己所学的数学知识计算该桥AF的长。如图11所示，该桥两侧河岸平行，他们在河的对岸选定一个目标作为点A，再在河岸的这一边选出点B和点C，分别在AB、AC的延长线上取点D、E，使得DE∥BC。经测量，[BC=120]米，[DE=210]米，且点E到河岸BC的距离为60米。已知[AF⊥BC]于点F，请你根据提供的数据，帮助他们计算桥[AF]的长度。

点评：本题先利用“A型”相似三角形求得一组对应边的比，再利用“X型”相似三角形求得桥长。其中AC∶CE是一组中间比，起着桥梁作用，沟通了两组相似三角形对应边成比例。已知点E到河岸的距离，过点E作BC的垂线是一条必然的辅助线。

五、利用相似三角形确定物距范围

利用相似三角形对应边成比例建立函数关系式，在对应边成比例的四个量中，有两个变量，这样就建立了函数关系式。

［例5］如图13所示，点光源O射出光线沿直线传播，将胶片上的建筑物图片AB投影到与胶片平行的屏幕上，形成影像CD。已知[AB=0.3] dm，胶片与屏幕的距离[EF]为定值，设点光源到胶片的距离OE长为x（单位：dm），CD长为y（单位：dm），当[x=6]时，[y=4.3]。（1）求EF的长；（2）求y关于x的函数解析式，在图14中画出图象，并写出至少一条该函数性质；（3）若要求CD不小于3 dm，求OE的取值范围。

图象关于直线[y=x+0.3]对称；函数图象无限地接近直线[y=0.3]与y轴。

由以上五个方面的分析发现，相似三角形的应用就是将现实问题转化为相似三角形问题，然后利用相似三角形的性质解决问题，比较常用的性质是相似三角形对应边成比例。