探究反比例函数图象与其他图形的结合

张新

［摘 要］反比例函数与其他图形的结合是中考数学命题的热点。文章结合几则典例，探讨反比例函数图象与一次函数图象、平行四边形、相似三角形、圆的结合，旨在提高学生解决问题的综合能力，培育学生的思维品质。

［关键词］反比例函数；图象；中考

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）29-0019-03

反比例函数是初中阶段学生学习的重点知识。中考数学当中，关于反比例函数的重难点考查，往往将反比例函数图象与其他图形结合，如与一次函数图象、平行四边形、相似三角形、圆结合，考查反比例函数的图象与性质、一次函数的图象与性质、平行四边形的性质与判定、相似三角形的性质与判定、圆的有关性质，以及数形结思想、方程思想、转化思想等。如何解决反比例函数与其他图形的结合问题呢？笔者结合具体实例加以阐释。

类型一、反比例函数图象与一次函数图象结合

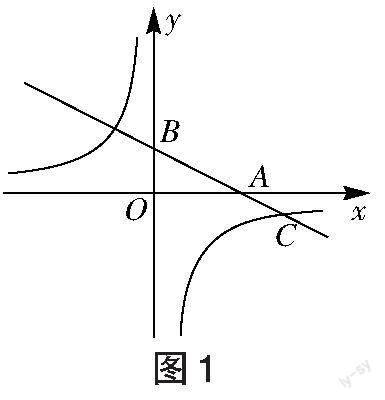
反比例函数图象与一次函数图象结合，比较常见的题型是已知两交点的坐标，求两个函数的表达式；根据两个函数图象的位置关系与交点坐标解不等式；连接两函数图象交点与原点形成三角形，求三角形的面积。笔者对下面的问题进行了创新设计，构造以反比例函数图象上一点、一次函数图象与坐标轴两交点为顶点的直角三角形，求未知点的坐标。

∴点P的坐标为（1，-6）或（3，-2）。

类型二、反比例函数图象与平行四边形结合

反比例函数图象既是中心对称图形，又是轴对称图形，对称轴是直线[y=±x]，而平行四边形是中心对称图形，对称中心是对角线的交点。过坐标原点任意画两条直线与反比例函数图象有四个交点，这四个交点组成的四边形是平行四边形，当这两条对角线相等时，形成的平行四边形是矩形。

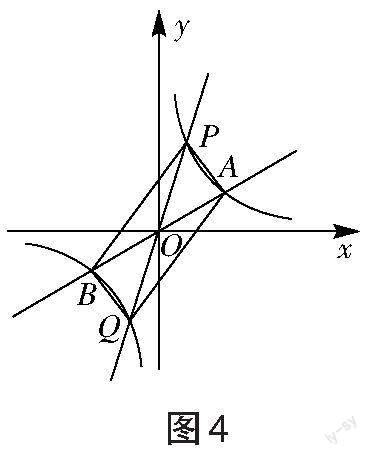
以下几个问题：（1）已知点A（3，1），那么点B的坐标是多少？（2）如图4所示，直线PQ是经过原点的一条直线，与反比例函数的图象分别交于点P、Q，①四边形APBQ是什么样的四边形？②已知点[A（3，1）]，点[P（1，t）]，则四边形APBQ的面积是多少？（3）已知m、n分别是点A、P的横坐标，当四边形APBQ是正方形时，m、n应满足什么条件？当四边形APBQ是矩形时，m、n应满足什么条件？

[P（1，3）]，由中心对称的性质，得点Q的坐标为（-1，-3）。如图5所示，分别过点A、B作y轴的平行线，分别过点P、Q作x轴的平行线，四条直线相交，得四邊形CDEF是矩形，由A、B、P、Q的坐标，得[CP=CA=2]，[DE=6]，[CD=6]，[DB=DP=4]，[BF=EQ=2]，[AF=QF=4]，所以[S四边形APBQ=S矩形CDEF-S△ACP-S△PDB-S△BEQ-S△AFQ=36-2-8-2-8=16]。

类型三、反比例函数图象与相似三角形结合

在反比例函数图象所在的平面直角坐标系内，构造直角三角形、等腰三角形或等边三角形，可以形成全等三角形或相似三角形。反比例函数的表达式显示了自变量与因变量的乘积恒为比例系数[k]，而相似三角形的对应边成比例，也可以转化为乘积式，所以反比例函数的图象也可以与相似三角形结合，构造反比例函数的综合题。

[BC⊥x]轴于点C，与反比例函数交于点[D（m，1）]，连接AD、DE。（1）求k的值与B点坐标；（2）求[S△ADE]；（3）若点P是直线AB上的动点，是否存在点P，使得[△BCP]与[△BDE]相似？若存在，求出此时点P的坐标；若不存在，请说明理由。

类型四、反比例函数图象与圆结合

反比例函数的图象既是轴对称图形，又是中心对称图形，而圆的对称性也是如此，兼具轴对称性与中心对称性两种特性，在平面直角坐标系内，反比例函数图象与圆会产生交点，这里的交点既满足反比例函数表达式，又满足圆的有关性质，这样就实现了反比例函数与圆这两部分知识的综合考查。

（2）由（1）可知，[A（-8，0）]，如图10所示，延长线段AM，交y轴于点K，连接OP、PQ，∵[∠QPO=90°]，∴[∠QAO=45°]，∴[△AOK]为等腰直角三角形，∵[A（-8，0）]，∴[K（0，8）]，设直线[AK]的表达式为

（3）如图11所示，过点P作[PF⊥AB]，交x轴于点E，交⊙P于点F和点H，分别过点F和点H作FH的垂线m、n，则垂线m、n即为⊙P的切线。过点F作[FG⊥OA]，交AB于点G。在Rt[△AOB]中，由勾股定理可得

反比例函数的图象还可以与二次函数的图象结合，两者的结合并不是两种图形的简单叠加，而是两种图形性质的综合应用。学生一方面要牢固掌握这两种图形的基本性质，另一方面还要熟悉这两种图形结合时，其中的命题模式与解题方法策略。学生只有不断积累解题经验，锻炼思维，才能更好地发展数学学科核心素养。