HPM视角下的“勾股定理”教学设计

王正阳　杨立英　周惠惠　吴新凤

［摘 要］随着HPM研究的逐步深入，基于培养目标和核心素养，将数学史、数学文化融入数学课堂的教学研究，已逐渐成为数学教育发展的方向。但是在教学实践中，仍然存在教师对数学史的知识讲解仅停留在介绍层面及忽视数学史在培养学生思维能力和人文素养等方面的作用等问题。文章以“勾股定理”的教学为例，探讨HPM理论在数学教学实践中的应用。

［关键词］HPM理论；勾股定理；教学设计

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）29-0001-03

近年来，随着课程改革的不断深入，我们的教学目标也逐步从“教书”扩展为“育人”，以“立德树人”为教育的根本任务建设“课程思政”，培养德才兼备、全面发展的社会主义建设者和接班人。数学史融入数学课堂，正是课程思政建设的重要途径。此外，《普通高中数学课程标准（2017年版2020年修订）》中也明确指出：“通过数学概念和思想方法的历史发生发展过程，一方面可以使学生感受丰富多彩的数学文化，激发数学学习的兴趣；另一方面也有助于学生对数学概念和思想方法的理解。”

本文选择义务教育阶段的数学课程“勾股定理”一节，在重构勾股定理历史的基础上进行教学设计，希望通过对此案例的分析，为将数学史融入教学实践的内容选择、融入方式、教学目标以及预期效果等方面的研究提供可行的思路与方法。

一、HPM理论

HPM是History and Pedagogy of Mathematics（数学史与数学教育）的简称，其主要研究内容包括数学史与教学法、数学史与学生认知发展规律、基于数学史的教学设计、数学与其他学科的关联、多元文化的数学等。对HPM研究历史进行追溯，要从1972年谈起。1972年，在第二届国际数学教育大会上成立了数学史与数学关系国际研究小组，标志着HPM成为一个学术研究的领域。而国内对于HPM的研究，则是从2005年全国第一届数学史与数学教育会议召开，时至今日，HPM已成为国内数学教育研究的一个重要方向。

汪晓勤教授提出了四种将数学史融入数学课堂的具体方式：附加式、复制式、顺应式、重构式。本文以“勾股定理”的教学设计为例，探讨将数学史融入数学课堂的方式。

二、勾股定理的歷史及其重构

（一）勾股定理的产生

1.赵爽弦图

公元前十一世纪，西周数学家商高提出“勾三、股四、弦五”，勾股定理因此得名。而我国对于勾股定理的应用，最早可追溯到大禹治水时期。

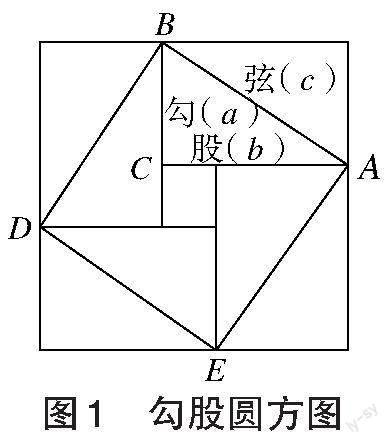
公元三世纪，数学家赵爽在注解数学著作《周髀算经》时提到：“勾股各自乘，并而开方除之，即弦。”赵爽创造了一幅“勾股圆方图”（如图1），对勾股定理进行了详细的证明，后世人们称之为“赵爽弦图”。

勾股定理是中国古代数学史上最杰出的成就之一。对于勾股定理的证明，相较于西方的毕达哥拉斯和欧几里得早了500多年。2002年在北京举办的国际数学家大会，也将“赵爽弦图”作为会徽（如图2）。

2.毕达哥拉斯定理

相传2500年前，古希腊数学家毕达哥拉斯在朋友家做客时，发现朋友家用地砖铺成的地面（如图3）中反映了直角三角形三边的数量关系：任意直角三角形，两直角边的平方和等于斜边的平方，即毕达哥拉斯定理。相传为了庆祝这一发现，毕达哥拉斯学派杀了一百头牛酬谢供奉神灵，因此毕达哥拉斯定理又称“百牛定理”。

（二）勾股定理的证明

勾股定理的证明方法有很多种，仅在清朝末年，我国数学家华蘅芳就提出了二十多种勾股定理的证明方法。除上述提到的证明方法外，值得一提的是，美国总统加菲尔德也给出了勾股定理的一种证明方法，通过“两个直角三角形面积[+]等腰直角三角形面积[=]直角梯形的面积”这一等量关系（如图4），即可得出勾股定理。

（三）勾股定理的应用

1.直接应用

如图5所示，[△ABC]和[△DCE]都是边长为4的等边三角形，点[B、C、E]在同一条直线上，连接[BD]，则[BD]的长为            。

2.实际应用

小莫妈妈买了一部42英寸（约106厘米）的电视机（如图6）。小莫量了电视机的屏幕后，发现屏幕的长和宽分别为85厘米和64厘米，他觉得一定是售货员搞错了，你同意他的想法吗？你能解释这是为什么吗？

解：42英寸的电视机指的是其屏幕对角线长为42英寸（约106厘米），因此，如图7所示构造直角[△ABC]，[AC=64]，[BC=85]，由勾股定理可得：[AC2+BC2=AB2]，[AB≈106]。

综上，电视机的尺寸是正确的。

三、“勾股定理”的教学设计

（一）勾股定理的提出与历史发展

教师利用多媒体展示勾股树（如图8），引入勾股定理，提问：它由哪些我们学过的基本图形组成？这个图案有什么特别的含义？

学生回答：勾股树是由大大小小的正方形组成的。

教师带领学生欣赏数学中的美，激发学生的学习兴趣和参与动机，并引导学生总结出组成上述图案的基本图形——三个正方形和其围成的直角三角形。

教师讲解：组成这一图案的基本图形，其实是在古希腊数学家毕达哥拉斯的朋友家的地板上发现的，这一个图案使得毕达哥拉斯大受启发，从而发现了非常著名的毕达哥拉斯定理。

教师通过“地板——毕达哥拉斯定理”这一夸张的设定，激发学生的好奇心和求知欲，进而向学生讲毕达哥拉斯发现这一定理的小故事，鼓励学生敢于思考、勇于发现。

（二）勾股定理的探索及证明

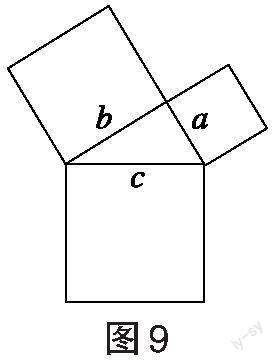
教师提问：如图9所示，已知直角三角形的两条直角边是[a、b]，斜边长为[c]，猜想一下它的三边之间有怎样的数量关系。

学生猜想：[a2+b2=c2]，勾股定理。（通过预习得到）

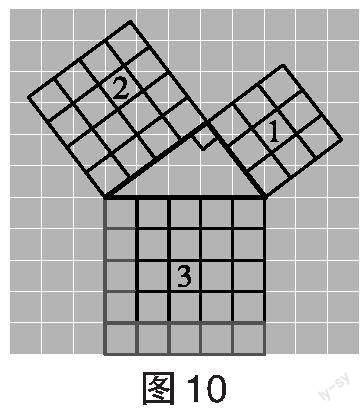
教师提问：将图9放在方格纸中（如图10），你能证明你的猜想吗？

学生证明：正方形1的面积[+]正方形2的面积[=]正方形3的面积。[32+42=25=52]。

教师引导：你能根据刚才的证明过程总结一下勾股定理的内容吗？

学生总结：直角三角形的两直角边的平方和等于斜边的平方。

教师提问：这样的一个定理在今天看来是不是特别简单、容易理解。据说当时为了庆祝这一定理的发现，毕达哥拉斯学派杀了一百头牛来酬谢供奉神灵，因此这个定理又称 “百牛定理”。

教师通过引导学生借助方格纸，找到[a、b、c]之间的数量关系，从而证明猜想，并且引导学生用数学语言对这一数量关系进行描述，即勾股定理的内容。

教师提问：同学们有没有觉得奇怪，明明是毕达哥拉斯发现的定理，为什么要叫作勾股定理呢？现在请同学们拿出你们课前准备的 4 个全等的直角三角形，思考怎样用这 4 个三角形拼成一个正方形？

学生小组合作，动手操作（如图11）。

教师讲授：其实早在公元前十一世纪，西周数学家商高就提出了“勾三、股四、弦五”，即三边长分别为3、4、5的直角三角形，这是勾股定理的一种特殊案例。他是最早提出勾股定理的人，勾股定理也因此得名。三国时期，有一位数学家赵爽，画出了一个和大家一样的图形，称之为“勾股圆方图”，后世人们把这个图称为“赵爽弦图”。赵爽利用这个图形，给出了世界上最早的勾股定理证明。既然同学们可以拼出和赵爽一样的图案，我相信同学们一定可以用此图证明勾股定理。

教师提问：还有同学有其他的拼法吗？

学生展示其他拼法（如图12）。

教师提问：可以用这个图形来证明勾股定理吗？请同学们课后思考。

教师通过引导学生动手操作，对 “赵爽弦图”的历史进行重温，帮助学生更好地理解勾股定理的内涵和证明过程，激发学生的探索欲望，培养学生的实践能力。同时，介绍我国在勾股定理的证明上早于西方500多年，帮助学生树立文化自信，培养学生的爱国情怀。

教师讲授：美国总统加菲尔德也贡献了一种非常巧妙的勾股定理证明方法（如图13），同学们可以试着证明一下吗？

教师引导学生用多种方法对勾股定理进行证明，培养学生的发散性思维和创新思维，并且鼓励学生树立信心，勤于思考，去探索更多的证明方法。

（三）勾股定理的应用

1.如图14所示，一个梯子[AB]长2.5 m，顶端[A]靠在墙[AC]上，这时梯子下端[B]与墙角[C]的距离为[1.5 m]，梯子滑动后停在[DE]的位置上，如图15所示，测得[BD]长为0.5 m，求梯子顶端[A]下落了多少米？

解：由题意易知 [AB=DE=2.5]，[BC=1.5]，[BD=0.5]，[CD=2]，

在[Rt△ABC]中，由勾股定理知[AB2=AC2+BC2]，[AC=2]。

[Rt△EDC]中，由勾股定理知[DE2=CD2+CE2]，[CE=1.5]，[AE=AC-CE=0.5]，所以梯子顶端[A]下落了0.5米。

2. 小明家新房装修，工人师傅搬来了一块长3米，宽2.2米的薄木板，能顺利通过门框（尺寸如图16所示）吗？为什么？

解：如图17所示，连接 [AC]。

在[Rt△ABC]中，由勾股定理知：

[AC2=AB2+BC2]，

因为[AC]大于木板的宽，所以木板能从门框内通过。

数学史融入课堂教学，不单单是讲故事，更要讲好故事。HPM视角下的数学教学要求教师要在浩如煙海的史学资料中选择恰当的、有深度的内容，通过对历史的借鉴、重温、改编和重构，深入挖掘其中的思想和价值观念，激发学生的学习兴趣，缓解学生的学习压力，提高学生的数学素养，帮助学生更好地理解知识的内涵和本质。

［   参   考   文   献   ］

［1］  杨孝斌，吴万辉，吕传汉，等.基于培育数学核心素养的行动：解题课例研析［M］.上海：华东师范大学出版社，2020．

［2］  张大鹏. 在数学教育中数学史的融入策略［J］. 中国科技博览， 2015（5）：264.

［3］  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订［M］.北京：人民教育出版社，2020．

［4］  汪晓勤，王苗，邹佳晨.HPM视角下的数学教学设计：以椭圆为例［J］.数学教育学报，2011（5）：20-23.