2023 年高考三角函数问题聚焦
■陶江华
2023 年高考对三角函数的考查主要围绕“三角函数的图像与性质”展开,考查重点为函数的单调性、奇偶性、周期性、对称性、最值、图像变换和零点,并常与三角恒等变换交汇命题。
聚焦1:三角函数的周期性和对称性的应用
例1 (2023年高考全国卷)若f(x)=为偶函数,则a=____。
解:函数f(x)=x2+(a-2)x+1+cosx为偶函数,其定义域为R。因为偶函数+偶函数=偶函数,余弦函数y=cosx为偶函数,所以二次函数y=x2+(a-2)x+1为偶函数,所以a-2=0,可得a=2。
体验:f(x)为奇函数⇔f(x)的图像关于原点对称,f(x)为偶函数⇔f(x)的图像关于y轴对称。如果函数f(x)是偶函数,那么f(x)=f(|x|)。既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空数集。
聚焦2:三角函数在区间上的单调性和最值
例2 (2023年高考上海卷)已知a∈R,记y=sinx在[a,2a]上的最小值为sa,在[2a,3a]上的最小值为ta,则下列情况不可能的是( )。
A.sa>0,ta>0 B.sa<0,ta<0
C.sa>0,ta<0 D.sa<0,ta>0
解:由给定区间,可知a>0。作出函数y=sinx的部分图像,如图1所示。
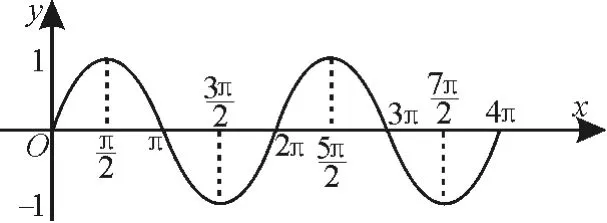
图1
区间[a,2a]与区间[2a,3a]相邻,且区间长度相同。

结合选项可得,不可能成立的是sa<0,ta>0。应选D。
体验:本题主要考查正弦函数在所给相邻区间上的单调性和值域。
聚焦3:利用三角换元法和辅助角公式求最值
例3 (2023 年高考全国卷)已知实数x,y满足x2+y2-4x-2y-4=0,则x-y的最大值是( )。
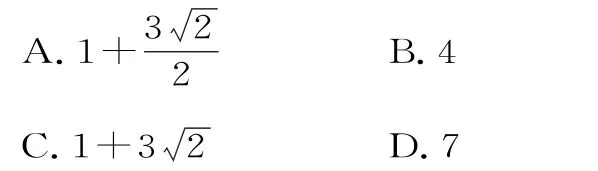
体验:本题的实质是点在圆上运动求点的横、纵坐标的差的最值。上述解法是通过三角换元,结合余弦函数的有界性求解的。
聚焦4:三角函数的探索性问题
例4 (2023 年高考北京卷)已知函数

(2)因为f(x)=sinωxcosφ+cosωx·sinφ,所以f(x)=sin(ωx+φ),所以f(x)的最大值为1,最小值为-1。
选择条件①。因为f(x)=sin(ωx+φ)的最大值为1,最小值为-1,所以2无解,条件①不能使函数f(x)存在。

体验:本题主要考查三角函数的图像与性质的应用,考查运算求解能力。


