高一上学年期末综合强化训练
■刘中亮(特级教师)
一、选择题
1.已知集合A={x|y=ln(x-1)},集合B={x|2x>1},则A∩B=( )。
A.(1,+∞) B.(0,+∞)
C.(0,1) D.(1,2)
2.若函数f(x)是R 上的偶函数,则“a=3”是“f(a-1)=f(2)”的( )。
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
A.与a无关,与b有关
B.与a有关,与b无关
C.与a有关,与b有关
D.与a无关,与b无关
4.已知奇函数f(x)在R 上单调递增,且f(1)=1,则关于x的不等式f(lnx) A.(0,1) B.(1,+∞) C.(0,e) D.(e,+∞) 5.已知函数f(x)是定义在(0,+∞)上的增函数,a=f(50.3),b=f(0.35),c=f(0.25),则a,b,c的大小关系是( )。 A.a>b>cB.b>a>c C.a>c>bD.c>a>b 6.近年来,“共享单车”的出现为市民“绿色出行”提供了极大方便。某共享单车公司计划在甲、乙两座城市共投资120万元,根据行业规定,每座城市至少要投资40万元。由前期市场调研可知:甲城市收益P(单位:万元)与投入a(单位:万元)满足P=3 2a-6,乙城市收益Q(单位:万元)与投入A(单位:万元)满足。则投资这两座城市收益的最大值为( )。 A.26万元 B.44万元 C.48万元 D.72万元 7.设x1满 足2x+lnx=5,x2满 足ln(2-x)-2x=1,则x1+x2=( )。 A.8 B.6 C.4 D.2 A.(-3,2) B.(-2,3) C.(-1,6) D.(-6,1) 9.(多选题)已知函数f(x)=x2+ax+b,集合A= {x|f(x)≤0},集合B=,若A=B≠∅,则实数a的取值可以是( )。 A.2 B.3 C.4 D.5 10.(多选题)若a,b∈(0,+∞),a+b=1,则下列说法正确的是( )。 11.(多选题)已知a>0,b>0,且a+b=1,则( )。 12.(多选题)已知函数f(x)=x2-1,则( )。 A.f(x+1)=(x+1)2-1 B.f[f(x)]=(x2-1)2-1 C.定义域为[- 1,0]时,值域为[- 1,0] D.值域为{-1,0}时,定义域为{-1,0,1} 13.(多选题)已知x0是函数f(x)=ex+2x-4的零点(其中e=2.71828…为自然对数的底数),则下列说法正确的是( )。 A.x0∈(0,1) B.ln(4-2x0)=x0 14.(多选题)已知α是锐角,则( )。 A.2α是第二象限角 B.sin2α>0 两天后,也就是小长假刚一结束,我便在老婆的陪同下,走进了市人民医院。之所以仅仅两天后我便在老婆的陪同下走进市人民医院,是因为我对区医院的那位专家已经完全失去了信心。 15.(多选题)已知函数f(x)=( )。 A.是奇函数 B.是偶函数 C.关于点(π,0)成中心对称 16.已知2a+3+4b=4a+2b+3(a,b∈R 且a≠b),则a+b的取值范围为_____。 21.已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且f(2)=1,对于任意x1,x2∈ (0,+ ∞),x1≠x2,都 有成立,则的解集为_____。 22.已知全集U=R,集合A={x|x2-2x-3<0},B={x1<2x<16}。 (1)求A∪B。 (2)设集合C={x|a 23.已知集合A={x|a-1 (1)若a=1,求A∪B,A∩(∁RB)。 (2)若A∩B=∅,求实数a的取值范围。 24.已知a,b为正实数,函数f(x)=x2-(a+2b)x+2ab。 (1)若f(1)=1,求2a+b的最小值。 (2)若f(0)=2,求不等式f(x)≤0 的解集(用a表示)。 (1)证明:函数f(x)在(0,1]上单调递减。 (2)求函数g(x)=f(x)+f(1-x)+的值域。 26.已知幂函数f(x)=(m-1)2·xm2-4m+2在(0,+∞)上单调递增。 (1)求m的值。 (2)若a>0,b>0,且a+b=m+1,求的最小值。 27.已知函数f(x)=2x(x∈R)。 (1)解不等式f(x)-f(2x)>16-9×2x。 (2)若关于x的方程f(x)-f(2x)-m=0在[-1,1]上有解,求m的取值范围。 (3)函数f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数,若不等式2ag(x)+h(2x)≥0 对任意x∈[1,2]恒成立,求实数a的取值范围。 (1)求函数f(x)的最小正周期和单调递减区间。 (2)求函数f(x)的值域。 一、选择题 1.提示:因为A={x|y=ln(x-1)}={x|x>1},B={x|2x>1}={x|x>0},所以A∩B=(1,+∞)。应选A。 2.提示:已知函数f(x)是R 上的偶函数,由f(a-1)=f(2),可得|a-1|=2,解得a=3或a=-1。由a=3成立,可得f(a-1)=f(2)成立,但由f(a-1)=f(2)成立,不一定有a=3成立,所以“a=3”是“f(a-1)=f(2)”的充分不必要条件。应选A。 4.提示:因为f(x)为奇函数,所以f(-lnx)=-f(lnx),所以原不等式可化为2f(lnx)<2,即f(lnx)<1。因为f(x)单调递增,且f(1)=1,所以lnx<1,解得x∈(0,e)。应选C。 5.提示:因为函数y=x5为R 上单调增函数,所以1>0.35>0.25>0。又因为50.3>1,函数f(x)是定义在(0,+∞)上的增函数,所以f(50.3)>f(0.35)>f(0.25),即a>b>c。应选A。 6.提示:由题意可得不等式组 7.提示:根据题意得ln(2-x2)-2x2=1,令2-x2=t,则lnt-2(2-t)=1,即lnt+2t=5。因为函数f(x)=2x+lnx在(0,+∞)上单调递增,又x1满足2x+lnx=5,所以2x1+lnx1=5,所以t=x1,即2-x2=x1,所以x1+x2=2。应选D。 12.提示:对于A,因为函数f(x)=x2-1,所以f(x+1)=(x+1)2-1,A 正确。对于B,因为函数f(x)=x2-1,所以f[f(x)]=f(x2-1)=(x2-1)2-1,B 正确。对于C,已知函数f(x)=x2-1,其定义域为[-1,0],函数在定义域内单调递减,由二次函数的图像和性质得其值域为[-1,0],C 正确。对于D,因为函数f(x)=x2-1的值域为{-1,0},所以函数对应的定义域为{-1,0,1}或{0,1}或{-1,0},D 错误。应选ABC。 13.提示:对于A,f(x)=ex+2x-4在R 上是增函数,f(0)=1-4= -3<0,f(1)=e+2-4>0,由零点存在性定理得函数的零点x0∈(0,1),A 正确。对于B,由f(x0)=ex0+2x0-4=0,可得4-2x0=ex0,两边同时取自然对数得ln(4-2x0)=x0,B正确。对于C,因为x0∈(0,1),所以2-x0>1,则x2-x00<1,C 错误。对于D,因为x0∈(0,1),所 以 2x0- e-x0+ 1 =,D 正确。应选ABD。 二、填空题 三、解答题 22.提示:(1)因为集合A={x|x2-2x-3<0}={x|-1 (2)因为集合C={x|a 23.提示:(1)易得B={x|x2-x<0}=(0,1)。由a=1,可得A={x|0 26.提示:(1)由幂函数的定义得(m-1)2=1,解得m=0或m=2。 当m=2 时,f(x)=x-2在(0,+∞)上单调递减,与题设矛盾,舍去;当m=0 时,f(x)=x2在(0,+∞)上单调递增,符合题意。 综上可知,m=0。
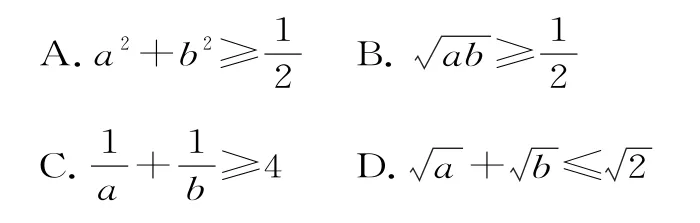
二、填空题

三、解答题