基于最小距离法的稳健群组变量选择

李 冬 梅, 王 明 秋, 王 秀 丽

(曲阜师范大学 统计与数据科学学院, 山东 曲阜 273165 )

0 引 言

近年来,变量选择问题逐渐成为统计学热点研究问题之一,随着数据采集能力的提高,人们所能收集到的变量数量越来越多,但是其中有很多变量可能是不重要的,且变量数量的增加会造成计算成本增大、最优化难以实现等问题,因此变量选择在数据分析中起着至关重要的作用．有效的变量选择不仅可以给出简洁易懂的模型,而且可以提高模型的可解释性和预测效果．变量选择的概念最初出现在20世纪60年代,一开始是通过子集选择法进行变量选择,主要有最优子集法和逐步法等,这些方法具有很强的实用性,但是也具有一些局限性,例如Fan等[1]指出最优子集法将参数估计与变量选择分开,因此参数估计会额外受到变量选择过程中带来的随机误差影响．目前广受欢迎的一类方法是基于惩罚函数的变量选择法,最早是Breiman[2]提出的nonnegative garrote(NNG)方法,之后Tibshirani[3]提出了可以同时进行参数估计和变量选择的Lasso方法,后来学者们又相继对Lasso方法进行改进,提出了多种单变量选择方法,如MCP方法[4]、Bridge方法[5]等．从Lasso惩罚函数开始,研究倾向于关注可微的损失函数和惩罚函数的特定组合,但这种特定组合大大增加了计算的复杂度,因此Liu等[6]利用Majorization-Minimization(MM)算法作为其核心优化引擎提出了一类通用算法,用于优化满足一定条件的各种非光滑惩罚目标函数．

在实际应用中,解释变量有时具有群组结构,例如考虑某个化学反应的反应速度这个多因子方差分析问题时,解释变量中包含反应温度、反应时间、催化剂种类,这3个解释变量均呈现分组结构,因此在这种情形下进行变量选择时,首先要能够正确地选择整组变量,特别地,在双层变量选择问题中合理的变量选择方法要求在正确地选择出整组变量的基础上还能够正确选择单个变量．在研究群组变量选择时,Zou等[7]提出了最早的具有群组变量选择功能的Elastic Net(EN)方法,该方法的惩罚函数包括两部分,其中岭回归部分可以处理具有多重共线性的数据,而Lasso部分可以进行变量选择．有时可以知道解释变量所具有的分组结构,Yuan等[8]最早提出了用于已知分组结构的Group Lasso方法,使用该方法选择群组变量时具有全进全出的特点,即整组变量同时选入或剔除,而不能在组内选择单个变量．但是在实际应用中,不仅要能选出重要群组变量而且需要进行组内单个变量的选择,因此产生了双层变量选择方法．Huang等[9]最早提出了进行双层变量选择的Group Bridge方法,该方法的主要思想是在组内和组间均采用单个变量惩罚函数．之后,Breheny等[10]又提出了组内和组间惩罚都是MCP函数的Composite MCP方法．

异常值会引起较大的偏差,从而影响模型的拟合效果,且通常会使得参数估计变大,但是在使用logistic回归模型的过程中发现极大似然估计(MLE)方法在解释变量异常值存在的情况下会引起参数内爆,即参数向量收缩为零向量[11]．于是在数据中存在异常值时,如果仍然使用极大似然估计方法进行参数估计,并基于Lasso方法[3]的惩罚函数进行变量选择,那么一些非零参数向量收缩为零向量会导致一些重要变量被忽略,从而会降低变量选择的准确率,进而降低模型的解释性和预测效果．因此,针对logistic回归模型的参数内爆现象,应该研究稳健的参数估计并进行群组变量选择和双层变量选择．针对异常值的问题,Basu等[12]提供了极大似然估计的一个稳健扩展,他们提出了一种最小散度估计方法来进行稳健的参数估计．而基于最小距离法的L2距离之前被用于解决分类问题,Kim等[13]使用L2距离来进行分类,他们对L2距离的应用主要是与非参数密度估计有关,而不是考虑稳定地拟合参数模型．Chi等[14]基于最小距离法研究了解释变量中存在异常值时logistic回归模型的变量选择方法,然而他们没有将该方法推广到自然群组变量选择和双层变量选择问题中,而且,目前还没有关于群组结构的logistic回归模型下基于最小距离法实现稳健群组变量选择的研究,这正是本文所做的工作．

1 模型与方法

1.1 Logistic回归模型

假设响应变量Y是0-1型随机变量,记Y的取值集合为χ={0,1}．现有n个独立同分布的观测样本(xi1,…,xid;yi)(i=1,…,n),则logistic回归模型可以表示为

(1)

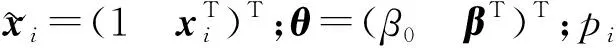
通常使用极大似然估计方法对logistic回归模型进行参数估计,由yi～B(1,pi)易知y1,…,yn的似然函数为

(2)

其负对数似然函数为

(3)

1.2 基于最小距离法的稳健参数估计

假设Pθ是随机变量Y的含有未知参数的概率质量函数,其中未知参数θ∈Θ,记Θ为参数空间,而真实的概率质量函数是P．假如P已知,那么一个直观的参数估计方法就是去寻找使得Pθ最接近P的参数．根据这个想法,可以考虑Pθ与P之间的L2距离,通过最小化该距离来得到上述logistic回归模型的参数估计．

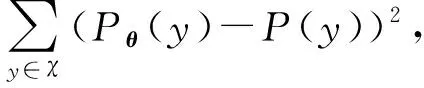
(4)

(5)

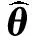
(6)

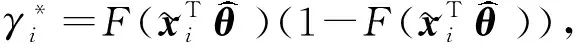
1.3 算 法

寻找上述logistic回归模型的L2估计量问题可以归结为求解一个目标函数最小值问题．由于MM算法在数值上表现稳定、易于操作并且也可以用来处理基于Lasso的惩罚函数,因此本文使用MM算法来求解这个最小化问题．但是MM算法不直接对目标函数进行最优化求解,而是寻找目标函数的近似替代函数,对这个替代函数进行迭代优化．每迭代一次,就寻找一个目标函数的上界函数,然后求这个上界函数的最小值,如此一来就可以将一个比较难的优化问题转化为一系列较为简单的优化问题．

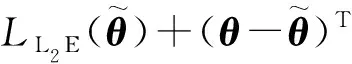
(7)

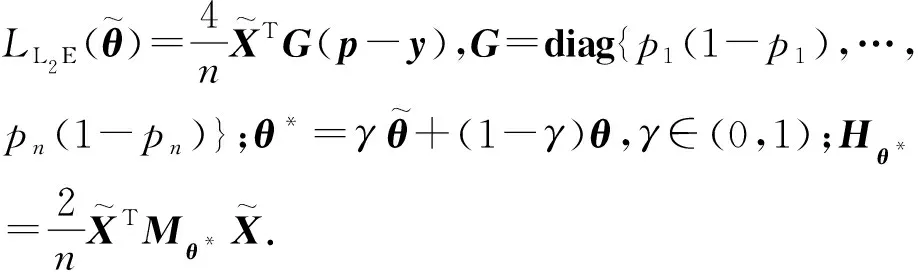
(8)

则可推出(Mθ*)ii≤η,从而有

(9)

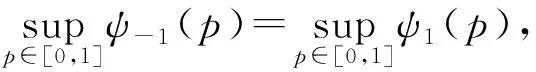
(10)

因此,目标函数LL2E的近似替代函数为

(11)

可以写成

(12)

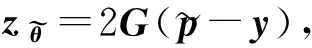
(13)

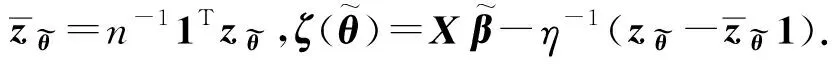
综上所述,最小化LL2E的MM算法可以写成如下步骤：

(2)利用下列迭代公式更新估计值：

(14)

(3)重复(2),迭代直至收敛,算法收敛性的证明详见文献[14]．

2 基于惩罚函数的变量选择方法

(15)

基于惩罚函数的群组变量选择方法主要是先通过加入惩罚函数对模型的整组参数β(j)进行约束,在这种约束性质下往往会产生一些恰好为零的系数;之后在约束条件下最小化损失函数,从而同时实现参数估计和群组变量选择．群组变量选择方法的目标函数一般可以表示为

(16)

式中：LL2E(β)为损失函数,Pλ(β(j))为惩罚函数,λ>0为调整参数．

仅能选择群组变量的惩罚函数可以表示为组间惩罚Po和组内惩罚Pi的复合函数：

(17)

其中组内惩罚Pi只作用在组内参数上,不具有变量选择功能．

本文主要使用以下3种仅能选择群组变量的惩罚函数：

(1)Group Lasso方法(GLasso)[8]

(18)

(2)Group MCP方法(GMCP)[15]

(19)

(3)Group SCAD方法(GSCAD)[16]

(20)

其中γ>2,

(21)

双层变量选择方法不仅能进行群组变量选择,而且能对组内变量进行单个变量选择,其惩罚函数可以表示为组间惩罚Po和组内惩罚Pi的复合函数,则第j组变量的复合惩罚函数可以表示为

本文主要使用如下3种双层变量选择方法的惩罚函数：

(1)Group Exponential Lasso方法(GEL)[17]

(22)

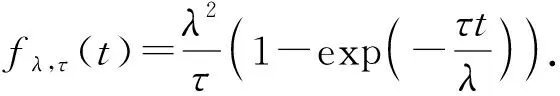
(2)复合MCP方法(CMCP)[10]

(23)

(3)Group Bridge方法(GBridge)[9]

(24)

3 数值模拟

为了较全面地通过数值模拟来检验L2E方法的有限样本表现,设计了两种不同类型的变量选择问题且同时考虑两种变量维数(p),结合上文中介绍的6种变量选择方法进行模拟,该模拟试验借助R语言的grpreg数据包实现．

惩罚函数中调整参数λ的选取对模型求解至关重要．先计算最大值λmax,然后设定最小值λmin为λmax的很小比例,如λmin=0.01λmax．本文利用训练集建立模型,然后利用验证集选取最优的λ．训练集中样本量为205,验证集中样本量为1 005,模拟重复1 000次．

例1考虑仅具有组稀疏的变量选择问题并且考虑两种变量维数d=20,40．数据生成过程为

yi～B(1,pi)

例2考虑具有双层稀疏的变量选择问题并且考虑两种变量维数d=30,60．数据的产生方式与例1类似,但每组大小为3．回归系数的真实值为

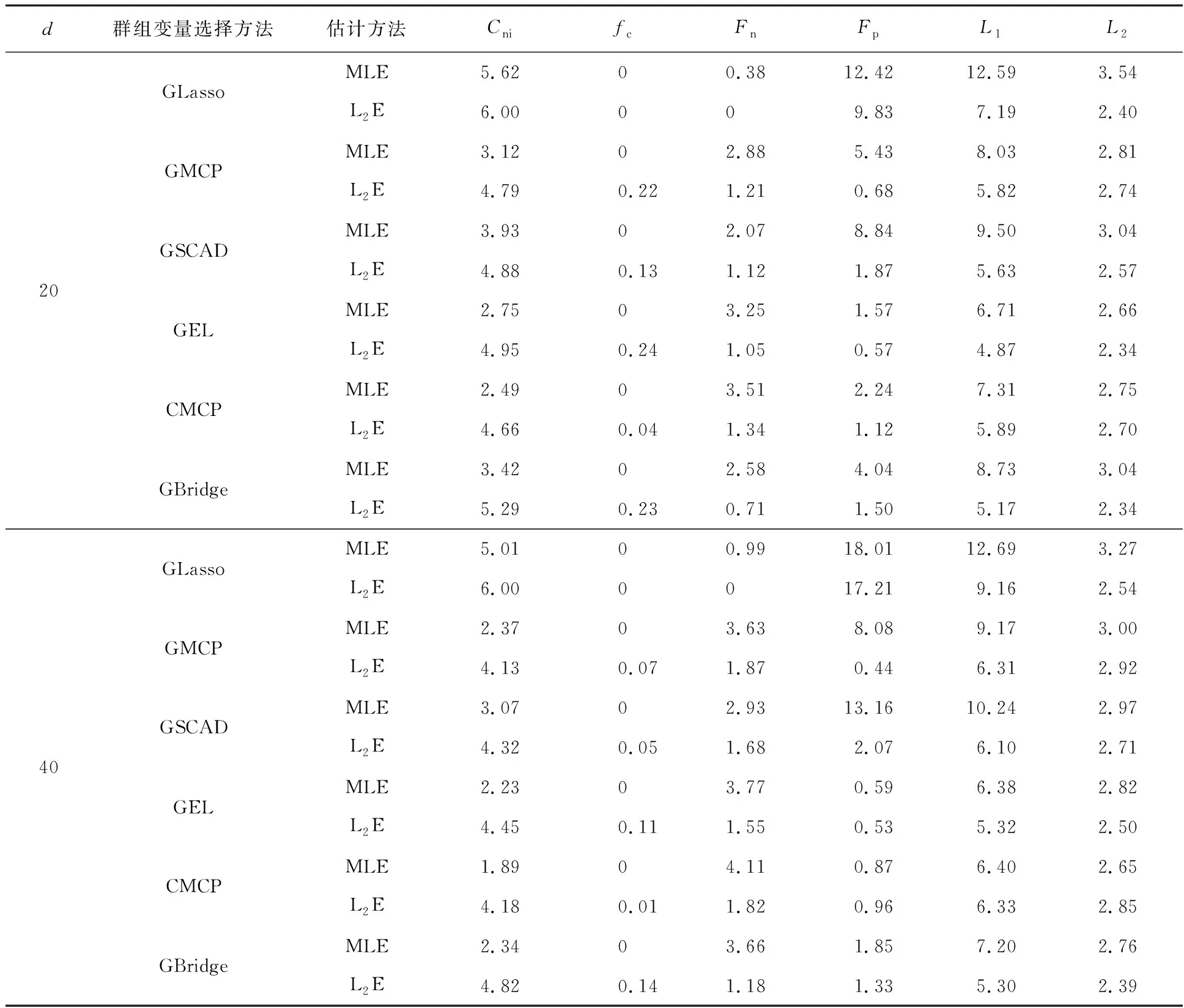
表1 例1的模拟结果

首先通过比较表1和表2中的L2E与MLE方法可以看出：(1)L2E方法总体上优于MLE方法,且不论变量维数为多少,MLE方法所得到的Fn都很大,这验证了在logistic回归模型中当解释变量存在异常值时,MLE方法确实容易把非零参数估计为零．(2)L2E方法比MLE方法选出正确模型的频率更高,且在该数值模拟中采用MLE方法时选出正确模型的频率均为零,因此在多次进行模拟试验中,使用L2E方法更有可能选出正确模型．综合来看,当logistic回归模型中解释变量存在异常值时,采用L2E方法更为合理,该方法对解释变量中的异常值稳健,减少了参数内爆对变量选择带来的影响,提高了变量选择的性能,降低了参数估计的误差．

然后,在采用L2E方法的条件下比较6种惩罚函数,可以得出：(1)根据表1和表2可知,GLasso方法的优点是能够正确选择出大部分重要变量,但同时会将不重要变量错选为重要变量,因此容易造成模型的过拟合,于是为了模型的简洁不应该优先选择GLasso方法．(2)根据表1可知,在组内不存在稀疏性,解释变量数量变化时,其余5种方法的衡量指标不相上下．根据表2的结果可知,在组内和组间均存在稀疏性时,使用双层变量选择的方法与使用仅选择群组变量的方法所得到的6个衡量指标差别也不是很大,这可能是因为重要变量的数量和群组规模比较小．综合比较表1和表2的结果可知,GBridge方法更胜一筹．综上所述,应该优先选择L2E结合GBridge方法所得到的目标函数进行稳健群组变量选择．

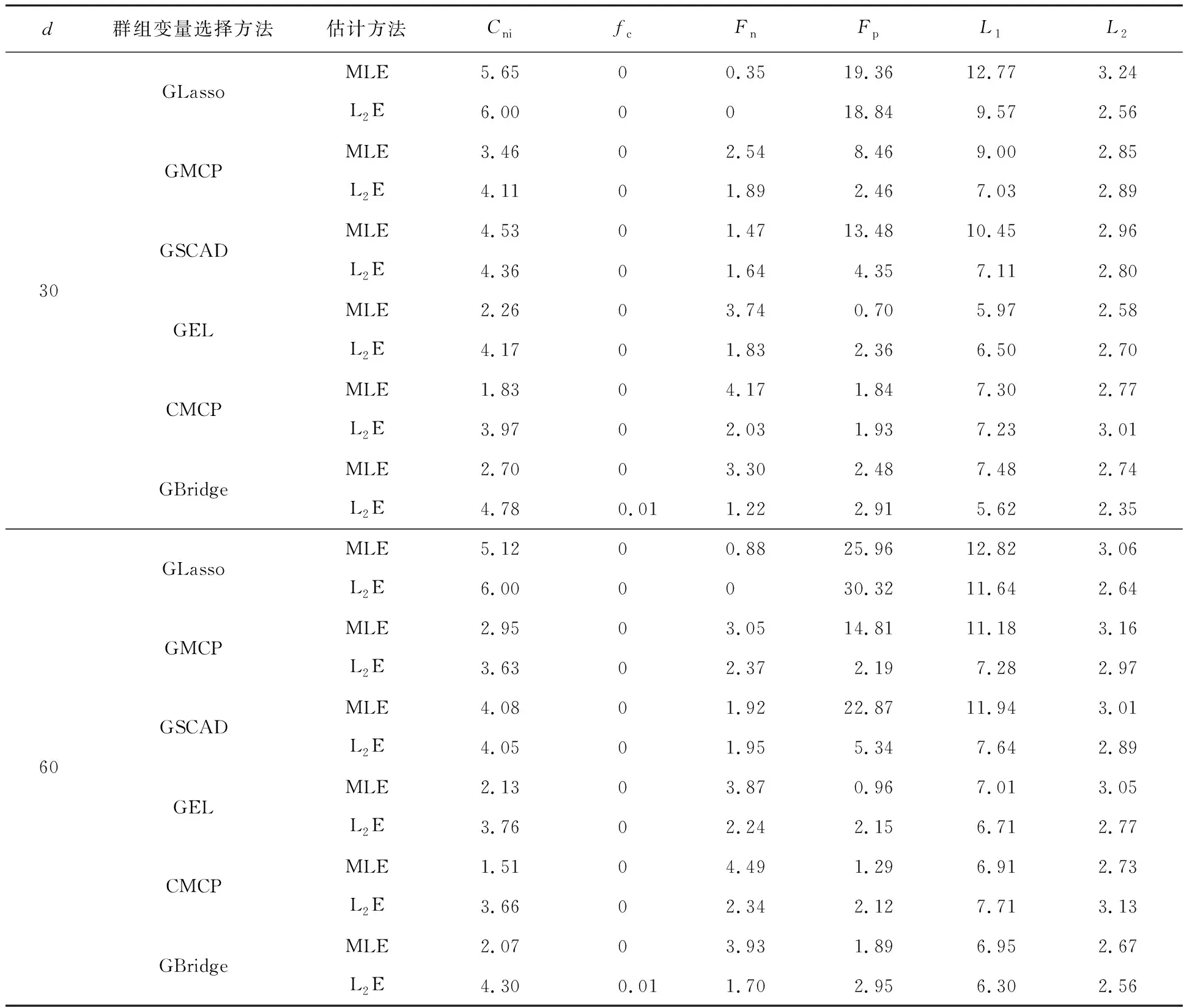
表2 例2的模拟结果

4 结 语

本文主要围绕logistic回归模型中解释变量存在异常值时的群组变量选择问题进行研究,首先基于最小距离法介绍了具有稳健性的L2E方法,当解释变量中存在异常值时,该方法能够减少回归系数缩减为零带来的对变量选择的影响;之后,利用MM算法得到了L2E的迭代公式;最后,通过数值模拟比较了基于L2E方法和MLE方法在模型具有组稀疏和双层稀疏的情况下,6种变量选择方法在不同维数下的有限样本表现,结果不仅验证了本文L2E方法的合理性,即在logistic回归模型中当解释变量存在异常值时L2E方法具有稳健性,而且指出了在这6种惩罚函数方法中使用Group Bridge方法进行变量选择的准确度更高．