基于相对结构度的水泥固化压实土力学与变形特性研究
李 吴 刚, 李 想, 杨 钢, 孙 秀 丽, 刘 文 化, 邵 伯
(1.江南大学 机械工程学院, 江苏 无锡 214122;2.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024;3.中建二局第二建筑工程有限公司, 广东 深圳 518000 )
0 引 言
由于土颗粒间胶结作用和空间排列形式不同,天然土与重塑土的力学和变形特性存在较大的差异[1].在土力学中将土颗粒间的胶结作用和空间排列形式称为土体的结构性[2].沈珠江[3]指出土体结构性是21世纪土力学研究的核心问题.李建红等[4]、谢定义等[5]的研究表明胶结作用和孔隙结构是结构性土的两大主要特征.土体的破坏往往伴随着结构性的衰变.研究土的结构性衰变规律有助于科学地预测土体的力学与变形特性,更好地为工程实践提供理论依据.近年来,关于土的结构性衰变规律研究取得了较大的进展.很多学者对此进行了比较深入的研究,李吴刚等[6]基于结构性土的变形特征,引入结构性土的本征压缩曲线,提出了相对结构度对结构性衰变进行分析.蒋明镜等[7]研究了土体结构性破损的微观机理,定义了结构性屈服面,反映了土体结构性的影响,再引入结构性损伤的破损参数,从而揭示出结构性土的衰变规律.祝恩阳等[8]通过结构性土的压缩变形规律推导了结构性土UH模型,揭示结构性土的衰变规律.Rouainia等[9]在重塑土本构关系中引入结构性参数并赋予其适当的演化规律,建立了结构性土的本构关系.Desai等[10]、Ouria[11]、刘维正等[12]、周成等[13]基于扰动状态概念建立了结构性土的本构关系.Liu等[14-15]在剑桥模型中引入结构屈服面和等效屈服面,建立了结构性土的本构模型.刘恩龙等[16]通过引入结构性破损参数,建立了基于岩土破损力学的结构性土的本构关系.谢定义等[17]通过引入综合结构势来描述结构性土的力学与变形特性.
表征土的结构性特征是建立可考虑结构性影响本构模型的关键,李吴刚等[6]基于土体结构的形成过程定义了土的相对结构度,采用该参数建立了结构性土的本构模型,可较好地预测结构性土的变形特性.但其定义该参数时并未考虑初始孔隙比及胶结强度对相对结构度衰变规律的影响,且该参数是否可用于描述由不同初始孔隙比和胶结强度导致结构性土抗剪强度的差异有待探究.因此本文研究人工制备水泥固化压实土试样,对其开展固结试验和固结排水剪切试验,并基于相对结构度研究水泥固化压实土的压缩特性与剪切特性.
1 水泥固化压实土试样制备
天然结构性土初始结构性间的差异和原位钻孔取样产生的扰动,使得难以从现场取得大量力学性状基本相同的土样,导致土样无法满足均一性的试验要求.为避免天然原状土不均匀性对研究产生不利影响,本文采用谢定义等[18]、蒋明镜等[19]提出的结构性土人工制备方法研究结构性对土力学与变形特性的影响,并探究水泥固化压实土变形过程中相对结构度的衰变规律.
1.1 试验土料
本试验所用的土料为黄土,取自山西省吕梁山,原状黄土呈颗粒状,较干.将土料烘干、碾碎并过0.5 mm筛后备用.按照《土工试验方法标准》(GB/T 50123—2019)[20]进行相应的土工试验,测定其基本物性指标:土粒相对密度为2.72,塑限Wp=21%,液限Wl=33%,塑性指数Ip=12.采用丹东百特(BT-2003)型激光粒度分析仪测定该黄土粒径,其结果如图1所示.

图1 试验黄土级配曲线
1.2 制样方法
为研究胶结作用和孔隙结构特征对水泥固化压实土力学与变形特性的影响,本文采用在土料中掺入水泥和食盐的方法控制试样的胶结强度和孔隙结构特征,水泥的水化产物可建立土颗粒间的胶结作用,食盐颗粒溶解可形成结构性土内的大孔隙结构.刘恩龙等[21]采用3.1%、5%和20%的水泥掺量研究结构性土的力学特性.Consoli等[22]采用3%、5%、7%和9%的水泥掺量研究水泥含量对人工结构性土强度参数的影响.Wang等[23]采用1%、3%、5%、7%、9%、11%和13%的水泥掺量对天然和人工结构性土的归一化特性进行研究.对水泥改性土的研究结果表明:水泥最佳掺量为土壤干质量的6%~8%.故本研究中水泥掺量为4%、6%和8%,初始孔隙比为0.8、0.9和1.0,水泥和食盐的掺量可见表1.水泥标号为P·O 42.5,食盐采用普通食用盐,为使食盐颗粒与土颗粒的粒径近似,需将食盐碾碎后过0.5 mm筛备用.不同孔隙比和水泥掺量条件下,土料的质量可通过下式计算:
(1)
式中:m为土料质量,Gs为土颗粒的相对密度,Gc为水泥的相对密度,ρw为水的密度,ac为水泥掺量,e为孔隙比,V为试样体积.
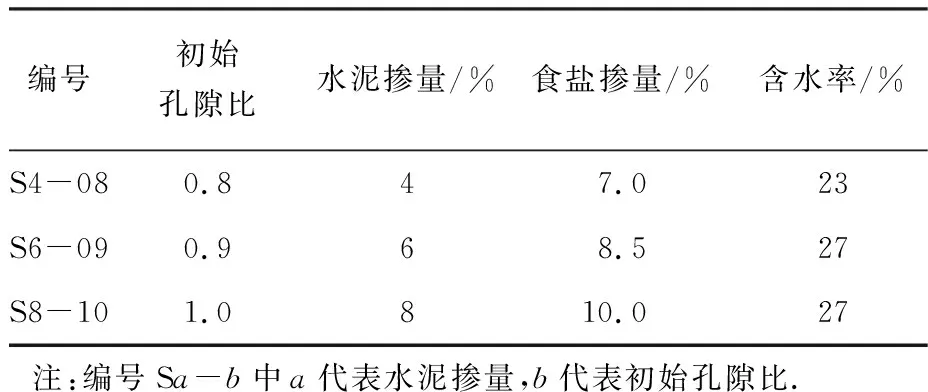
表1 水泥固化压实土的食盐和水泥掺量
将烘干后的黄土、水泥和食盐按照设定的质量配比充分拌和,随后称取一定质量的混合料分别倒入φ39.1 mm×80 mm的三瓣模和φ61.8 mm×20 mm的环刀中,采用压样法制备三轴试样和环刀试样,其中三轴试样分3层压实.试样制备完成后需去除试样内的食盐颗粒以形成水泥固化压实土内的大孔隙结构.刘恩龙等[21]、罗开泰等[24]采用在水中浸泡的方法溶解试样内的食盐颗粒,但是该方法耗时长且易有食盐颗粒残留,影响后续的试验结果.为解决该方法的缺陷,本文设计了图2所示的盐分去除装置,试样装入该装置后,在装置内加入适量的水,在渗流过程中,作用在试样上的位置水头保持恒定,水在重力作用下于试样上部经由土颗粒间的孔隙从试样底部排出,试样内的食盐颗粒溶于水后可在渗流作用下快速排出试样.为防止渗流作用破坏试样内的孔隙结构,在试样放入去盐装置前需在试样表面喷洒适量的水使试样保持湿润,水在重力和毛细作用下渗入试样内部后与水泥发生水化反应,并在土颗粒间生成胶结物质.试样静置24 h后,水泥达到终凝,试样内的胶结结构基本形成.随后将试样放入图2所示的盐分去除装置,试样内的食盐颗粒在渗流过程中逐渐溶解排出.当试样内的食盐被完全排出后(判断标准为风干试样表面没有白色晶体析出),将试样放入恒温恒湿的养护箱(温度(20±2)℃,湿度大于95%)中养护90 d,得到人工制备的水泥固化压实土试样.

(a) 装置实物图
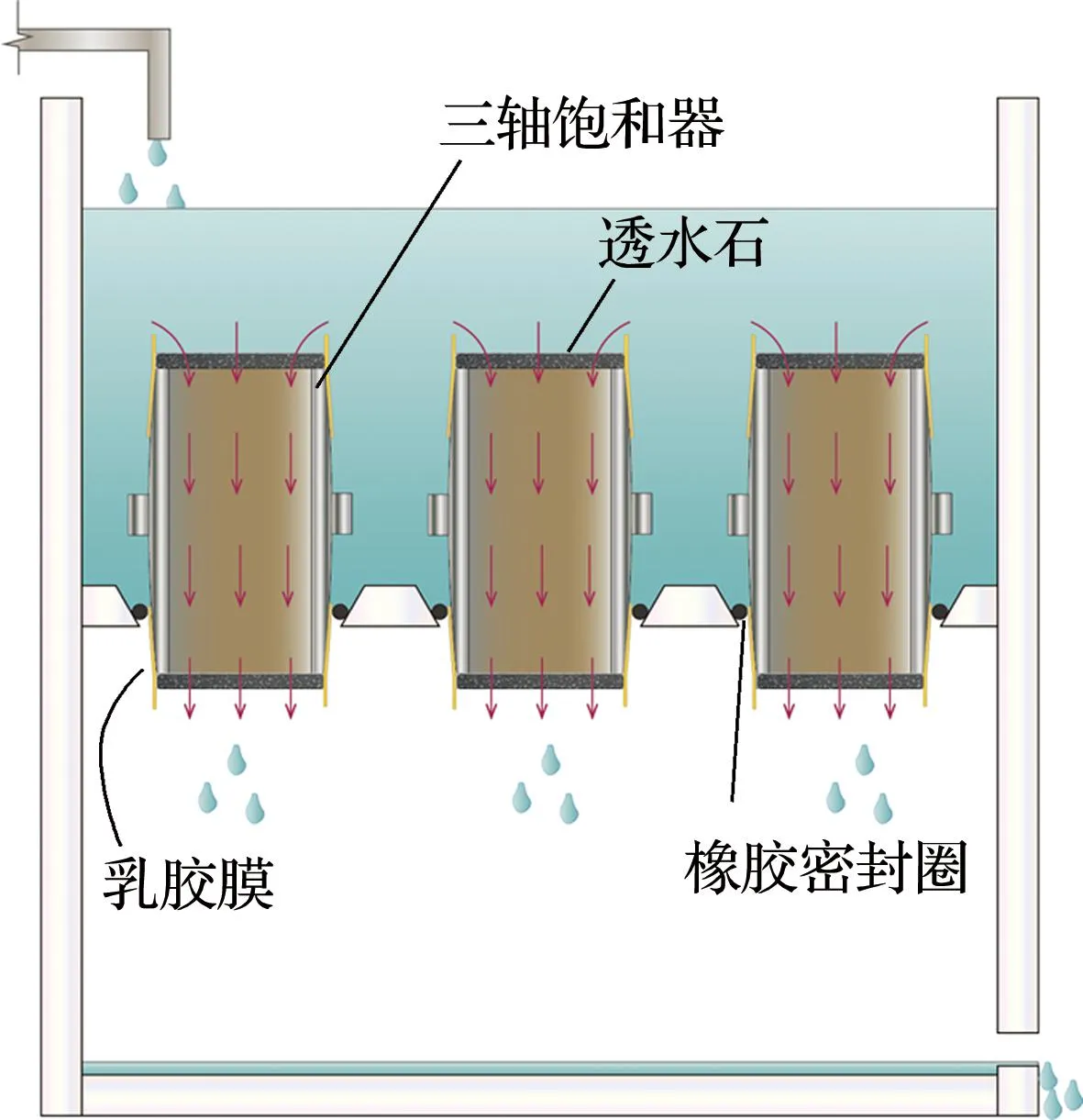
(b) 装置示意图
为研究水泥固化压实土和重塑土力学性质间的差异,在试样养护完成后,将具有同种水泥掺量的人工制备水泥固化压实土试样烘干后碾碎,以破坏土体的结构性,再过0.5 mm筛,参照《土工试验规程》(SL/T 237—1999)[25],采用压样法分3层压实,得到本试验所需的重塑土试样.
2 试验结果
为研究结构性对土力学与变形特性的影响,将抽真空饱和后的水泥固化压实土试样和重塑土试样分别进行固结试验和固结排水剪切(CD)试验.按照《土工试验方法标准》(GB/T 50123—2019)[20],固结试验的荷载等级为12.5、25、50、100、200、400、800、1 600、3 200 kPa;CD试验的围压为50、100、200 kPa,剪切速率为0.01 mm/min.
2.1 水泥固化压实土的压缩特性
相同初始孔隙比条件下不同水泥掺量的水泥固化压实土试样和重塑土试样的固结试验结果如图3所示(p表示竖向应力,编号S代表水泥固化压实土,R代表重塑土).由试验结果可知,在相同的应力状态下,水泥固化压实土试样的压缩曲线位于重塑土试样的上方.在固结曲线的弹性阶段,水泥固化压实土试样压缩曲线比较平缓,其斜率小于重塑土试样的,表明水泥水化形成的胶结物质有效提高了试样的初始刚度.随着竖向应力的增大,试样S4-08压缩曲线的斜率先于试样S6-08和S8-08出现增长,逐渐变陡,并不断趋近于重塑土试样的.试样S6-08和S8-08的压缩曲线也表现出和试样S4-08相同的发展趋势,但S6-08试样的水泥掺量低于试样S8-08的,试样S6-08的土体结构先发生破坏,故试样S6-08压缩曲线的斜率先于S8-08试样出现增长.由上述试验结果可知,土骨架的稳定性与试样内部胶结物质的含量有关,水泥掺量越高,由水泥水化产物提高的土骨架稳定性越显著,土体的结构性越强.
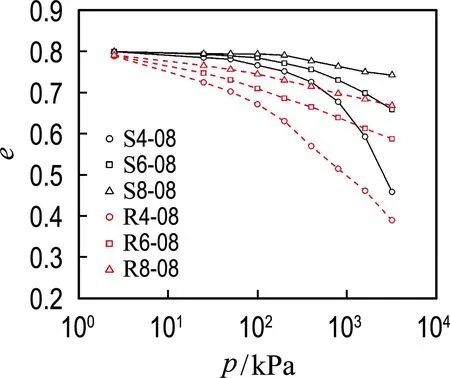
图3 初始孔隙比为0.8试样的压缩曲线
相同水泥掺量条件下不同初始孔隙比的水泥固化压实土固结试验结果如图4所示.试验结果表明,在固结试验的初始阶段,水泥固化压实土试样处于弹性状态,各试样的压缩曲线较平缓,在相同水泥掺量条件下,初始孔隙比为1.0的试样斜率最大,初始孔隙比为0.8的试样斜率最小.随着应力的增大,试样内部的土颗粒间发生相对滑移,试样由弹性状态进入弹塑性状态,压缩曲线的斜率急剧增大,以Δe表示初始孔隙比和交点处孔隙比的差值(图4(a)).由试验结果可知:Δe1.0>Δe0.9>Δe0.8,表示相同荷载下,初始孔隙比为1.0试样的结构性最容易发生破坏.水泥掺量6%和水泥掺量8%条件下也可发现相同的试验结果(图4(b)和图4(c)).随着固结压力的继续增大,各试样呈Δe越大,压缩曲线的斜率越大的趋势,且试样压缩曲线越接近于重塑土试样的压缩曲线.该组试验结果表明,增大初始孔隙比会弱化土体的结构性,试样的初始孔隙比越高,加载过程中土体结构越容易发生破坏.
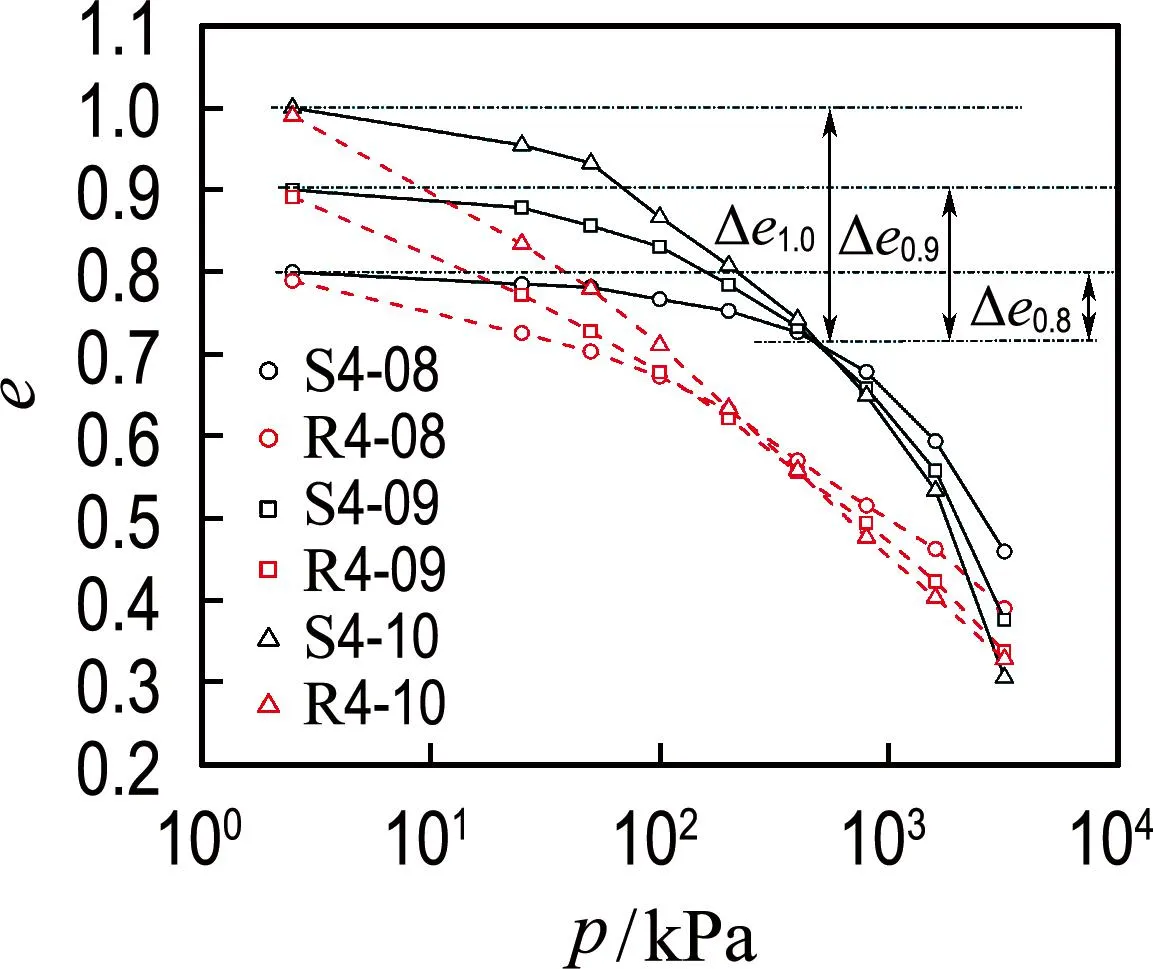
(a) 水泥掺量4%

(b) 水泥掺量6%
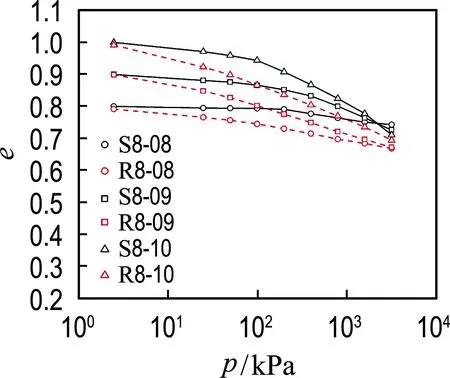
(c) 水泥掺量8%
综上,胶结作用会强化土体结构,而增大初始孔隙比会弱化土体结构,使得相同荷载下土体结构的完整性随着水泥掺量的增加而增大,但随着初始孔隙比的增大而减小.
2.2 水泥固化压实土的剪切特性
图5~7为初始孔隙比为1.0、0.9和0.8水泥固化压实土的剪切试验结果.虽然图中水泥固化压实土试样的应力-应变曲线形态与超固结土都具有应变软化的特点,但水泥固化压实土试样在应变软化时体应变εv的发展趋势与超固结土具有显著区别,超固结土在应变软化的过程中往往伴随着体胀的发生,而本研究中的水泥固化压实土试样体应变以剪缩为主,表明两者发生应变软化现象的力学机制不同,证明了本研究中的水泥固化压实土试样力学特性区别于重塑土的根本原因是土体结构性不同.
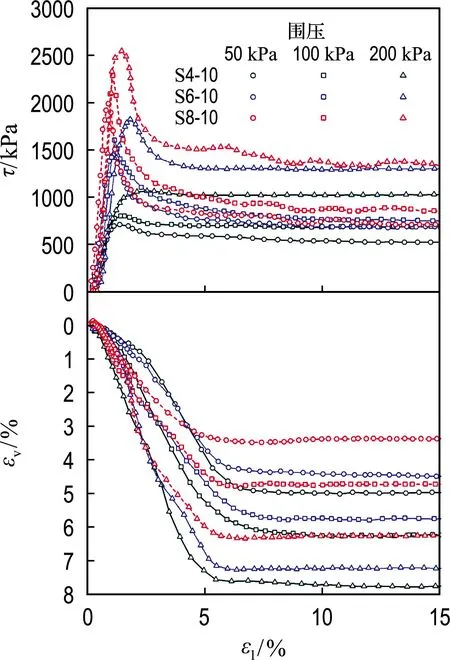
图5 初始孔隙比为1.0水泥固化压实土的剪切

图6 初始孔隙比为0.9水泥固化压实土的剪切
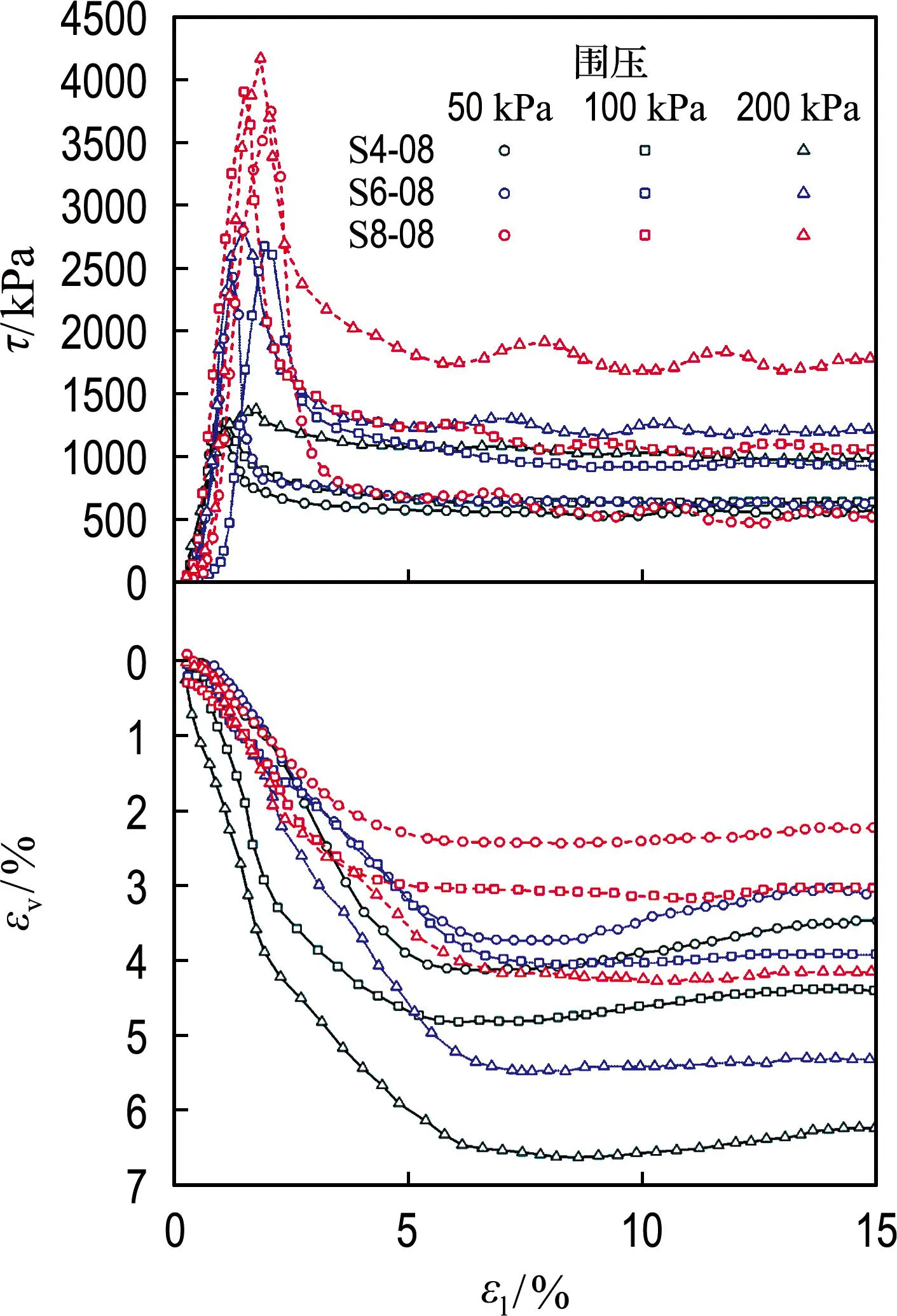
图7 初始孔隙比为0.8水泥固化压实土的剪切试验结果
由试验结果可知,水泥固化压实土试样在剪切过程中发生了显著的应变软化现象.在初始孔隙比相等的条件下,水泥水化产物在土颗粒间生成的胶结物质限制了土颗粒的相对滑移,提高了土体强度,故水泥固化压实土试样的应变软化主要由土颗粒间的胶结结构发生破坏所致.试验结果表明,胶结作用越强,胶结结构发生破坏时的应力跌落越显著,因此试样的应变软化现象也越明显;相反,胶结作用越弱,试样的应变软化现象越微弱.与此同时,在剪切试验开始前的固结阶段,围压的增长也会破坏试样的胶结结构,故在200 kPa围压条件下S4-10、S4-09、S4-08试样的应力-应变形态与重塑土的较为相似,只表现出轻微的应变软化现象.增大试样的初始孔隙比会弱化结构性,导致变形过程中土体结构更容易被破坏,故在相同水泥掺量和围压条件下,初始孔隙比较大的试样,其应变软化现象并不显著,而初始孔隙比较小的试样仍出现了较明显的应变软化现象.
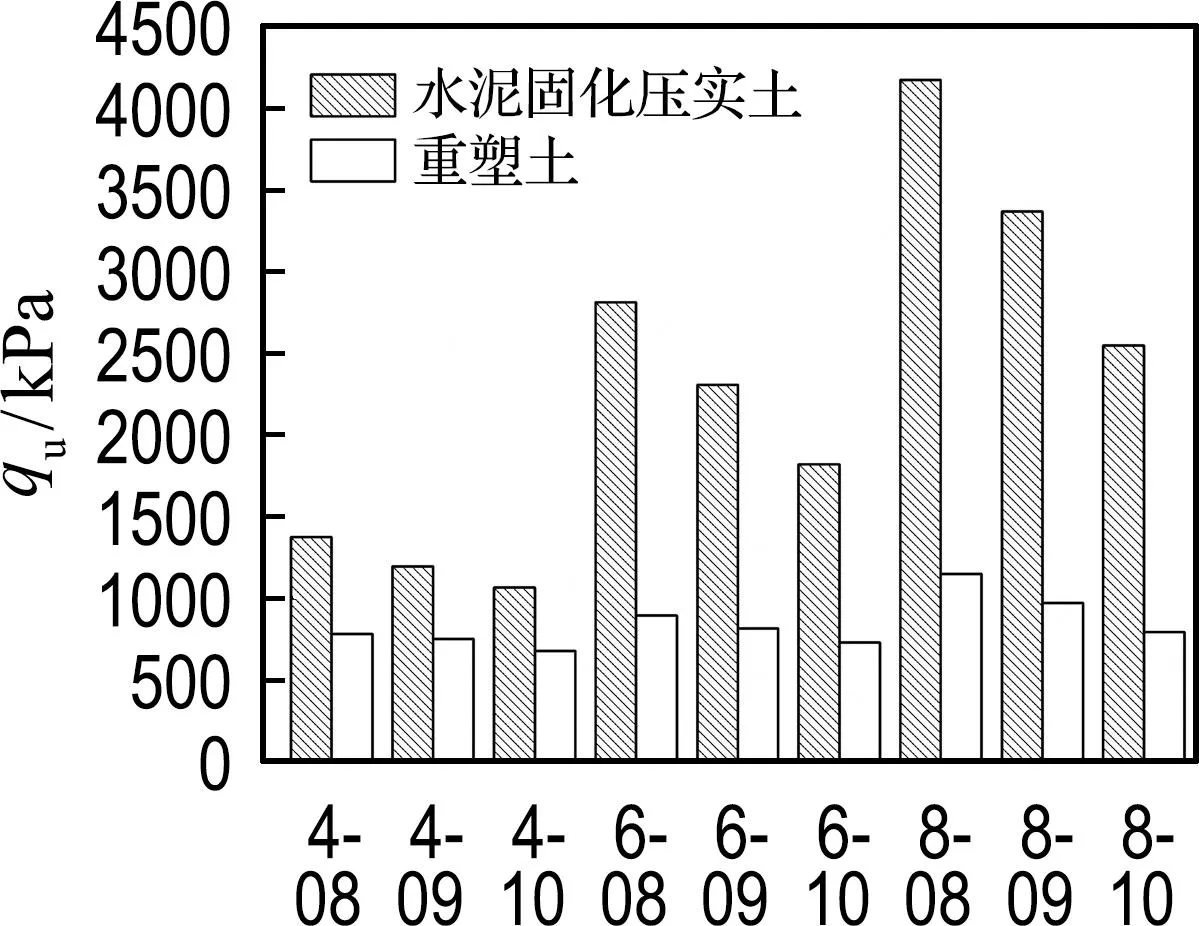
图8为50、100、200 kPa围压下水泥固化压实土试样与重塑土试样的峰值应力.由试验结果可知,水泥水化后生成的胶结物质(图9水泥固化压实土试样的SEM图像所示)提高了土骨架的稳定性,故水泥固化压实土试样的峰值应力随着水泥掺量的增加而升高.而增大初始孔隙比会弱化胶结作用的影响,使得试样的结构性更容易被破坏,故在相同水泥掺量时,水泥固化压实土试样的峰值应力随着初始孔隙比的升高而减小.根据临界状态土力学,土体的抗剪强度与试样的平均主应力有关,故当围压增长时,重塑土的峰值应力出现显著增长,200 kPa围压条件下,重塑土试样的峰值应力约是50 kPa围压时的3倍,如图8所示;但水泥固化压实土试样的峰值应力随着围压的增大仅出现了微弱的增长,这是由于围压的增长会破坏试样的结构性,导致由结构性提高的抗剪强度出现衰退,故试样的峰值应力仅出现微弱的增长,使得水泥固化压实土试样峰值应力与重塑土试样峰值应力的差值随围压的增大而降低.
图9所示为水泥固化压实土试样的SEM图像.图中,黄色菱形表示生成的纤维状的C-S-H凝胶类水化产物,C-S-H凝胶是水泥水化产物水化硅酸钙;红色圆圈表示土体内的孔隙结构,可以看出盐溶后形成的孔隙结构较为明显且分布比较均匀.由图可知,试样在相同养护条件下,水泥掺量越高,生成的水化产物越多,胶结作用越强;减小试样的初始孔隙比,可减小土颗粒间的孔隙,试样更为密实,土骨架愈趋稳定.因此,在较高水泥掺量和较小初始孔隙比条件下,试样的结构性强,其抗剪强度也大.

(a) 50 kPa围压
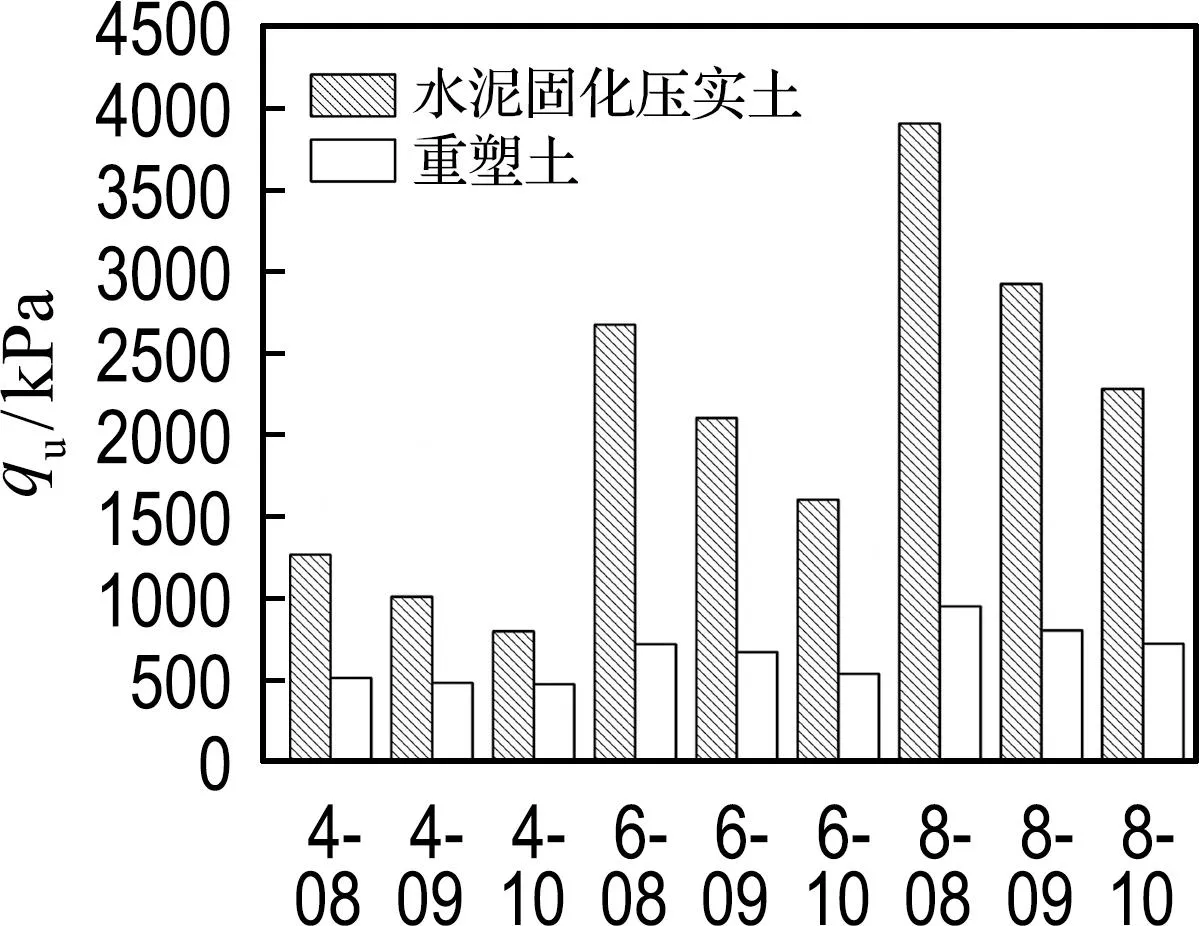
(b) 100 kPa围压
(c) 200 kPa围压

(a) S8-10

(b) S4-08
3 试验结果讨论
3.1 相对结构度衰变规律分析
本文采用李吴刚等[6]提出的相对结构度对本文的试验结果进行分析,如图10所示,假设某结构性土试样在压缩过程中其土体结构始终不发生破坏,则其压缩曲线可用图10中的虚线表示,将其定义为该结构性土的本征压缩曲线(ISCL),该曲线表征了土体结构不发生破坏时结构性土的压缩特性.但现实的土体在达到屈服应力后,土体结构必然发生破坏,试样的压缩曲线在达到屈服应力后逐渐偏离ISCL,如图10中红色曲线所示,将其定义为结构性土的压缩曲线(SCL).当土体结构完全破坏时,其压缩曲线与重塑土的压缩曲线(NCL)重合.因此,结构性土的压缩曲线位于以ISCL和NCL为边界的区域内.相对结构度以下式表示:
ξ=eS/eI
(2)
式中:eI为相同应力下ISCL和NCL之间的距离(图10),其值表示结构完整的结构性土所能承受的额外孔隙比;eS为相同应力状态下SCL和NCL之间的距离,其值表示当前应力状态下结构性土承担的额外孔隙比.
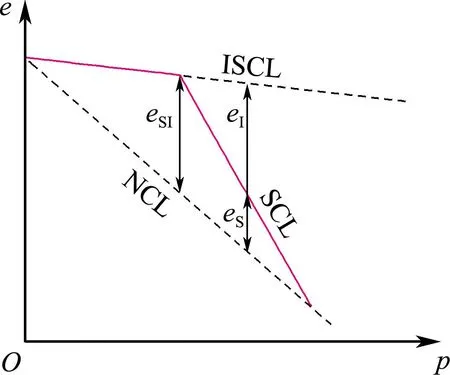
图10 结构性土的压缩特性
李吴刚等[6]提出的相对结构度发展式并未考虑塑性体应变的发展对相对结构度的影响,而土体结构破坏常伴随着塑性体应变的发展,因此采用本文的试验结果整理相对结构度与塑性体应变的关系,得到图11中的结果.根据试验结果可知,在相同水泥掺量条件下,虽然试样的初始孔隙比越大相同荷载下的相对结构度越小,但是不同初始孔隙比试样的相对结构度与塑性体应变间的关系曲线基本重合,表明在相同水泥掺量条件下初始孔隙比并不影响相对结构度随塑性体应变的发展变化速率.对图11中不同水泥掺量条件下相对结构度与塑性体应变间的关系曲线进行拟合分析,得到相对结构度-塑性体应变间的关系用下式表示:
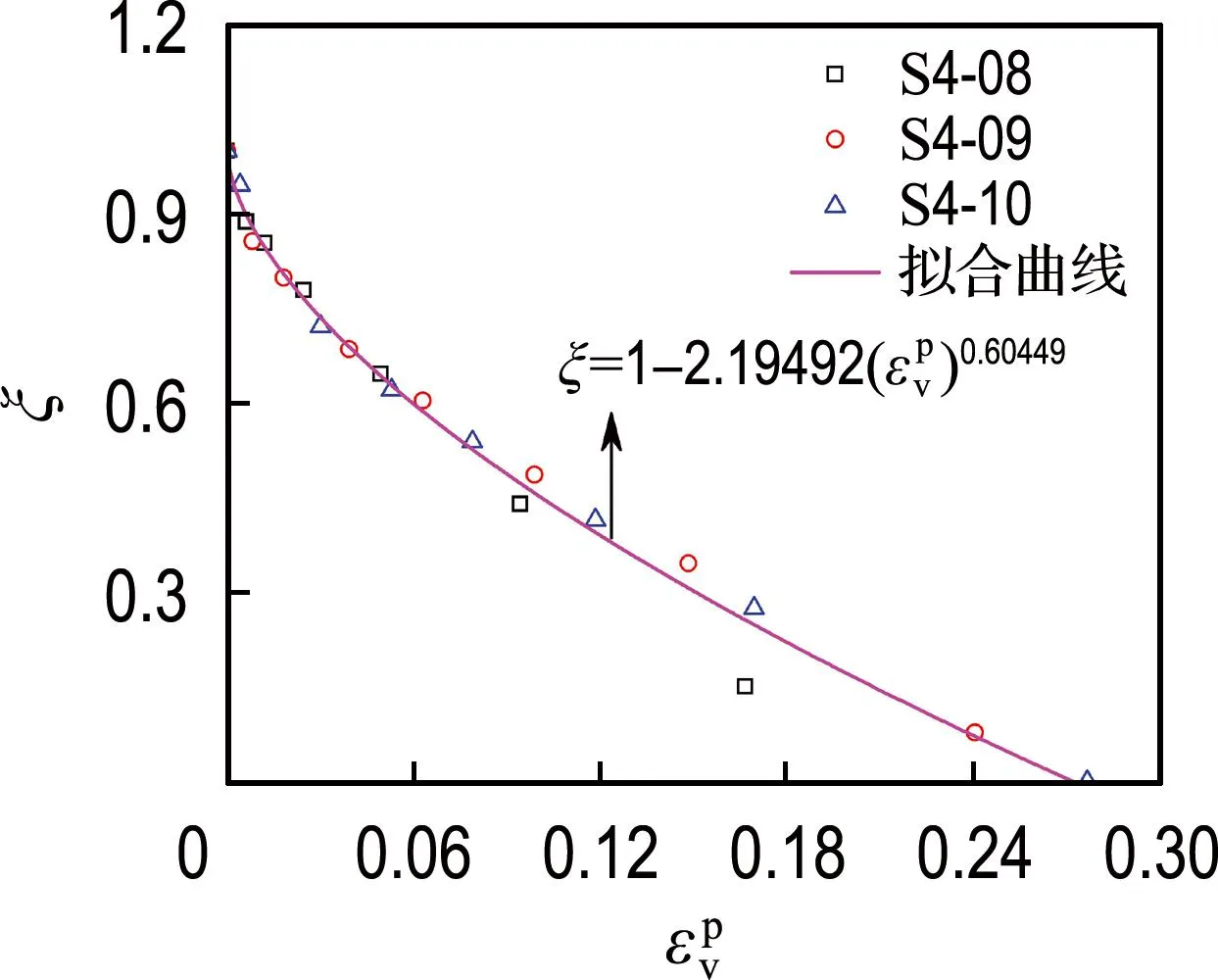
(a) 水泥掺量4%
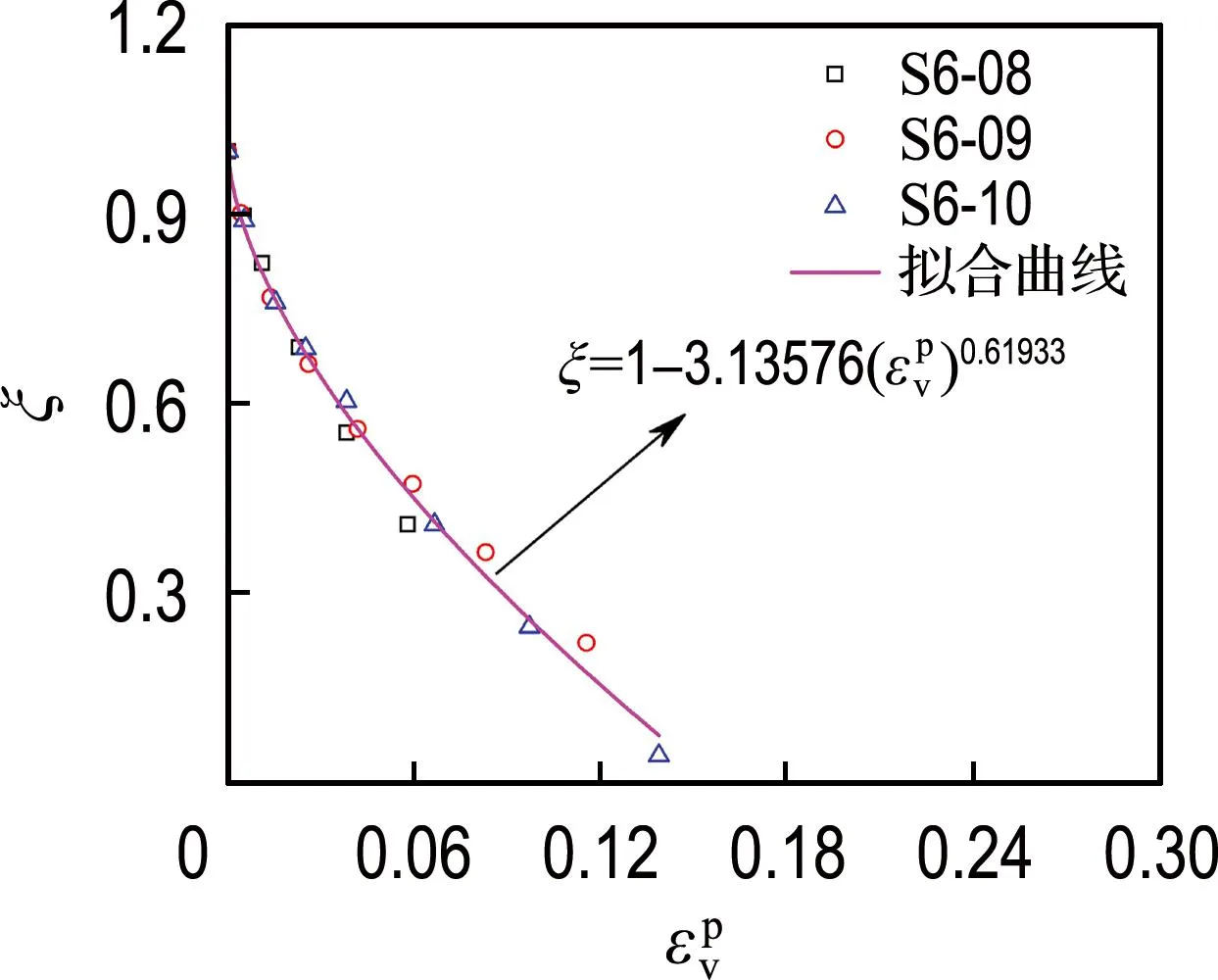
(b) 水泥掺量6%
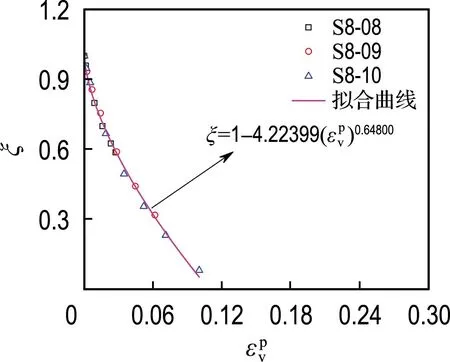
(c) 水泥掺量8%
(3)
不同水泥掺量条件下参数a和b的值见表2,参数b在不同水泥掺量条件下的值较为接近,表明水泥掺量对参数b基本无影响.参数a随着水泥掺量的增加而增大,表明塑性体应变增量相同时,水泥掺量的增加会显著提高相对结构度随塑性体应变的发展速率,即高水泥掺量试样比低水泥掺量试样的土体结构破坏更为严重,在宏观上表现为高水泥掺量试样具有更大的刚度并显现出脆性,而低水泥掺量试样的刚度小并显现出一定的延性.虽然初始孔隙比并不影响材料参数a和b的值,但增大初始孔隙比会弱化土体结构,在相同荷载下使得试样具有更大的塑性体应变,进而降低试样的相对结构度.综上,式(3)给出了相对结构度与塑性体应变的关系,能综合考虑胶结作用和初始孔隙比的影响,较好地描述了试样结构性衰变特性.

表2 拟合参数
3.2 相对结构度对峰值应力的影响
为研究结构性对土体抗剪强度的影响规律,本文对相对结构度与峰值应力的关系进行分析,基于图5~7中剪切试验结果可得到水泥固化压实土试样在不同围压下的峰值应力,并将各试样峰值应力时的塑性体应变代入式(3)后得到各试样峰值应力时的相对结构度,结果如图12所示.在荷载增加的过程中,试样的结构性随着塑性体应变的发展被逐渐破坏,相对结构度也随之减小,导致土骨架的稳定性降低,因此各试样的峰值应力随着相对结构度的降低而减小.从曲线的拟合结果可知,试样峰值应力与相对结构度呈幂函数关系.对比图12(a)、(b)和(c)可知,拟合曲线中的参数β、χ均随着围压的升高而减小,表明相对结构度对峰值应力的影响随着围压的升高而减小,这是由于围压的升高会导致土体结构破坏,原本由土体结构承担的这部分峰值应力出现降低,而围压的升高也会提高试样的峰值应力,这两种不同原因导致的峰值应力变化部分抵消,故在宏观上表现出相对结构度对峰值应力的影响随着围压的升高而降低.
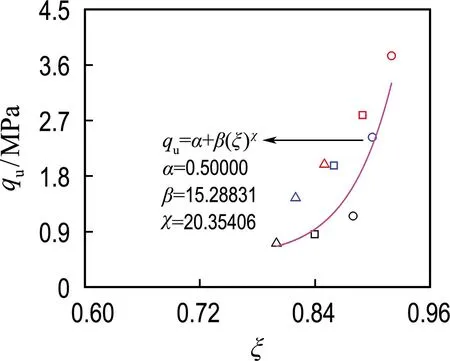
(a) 50 kPa围压
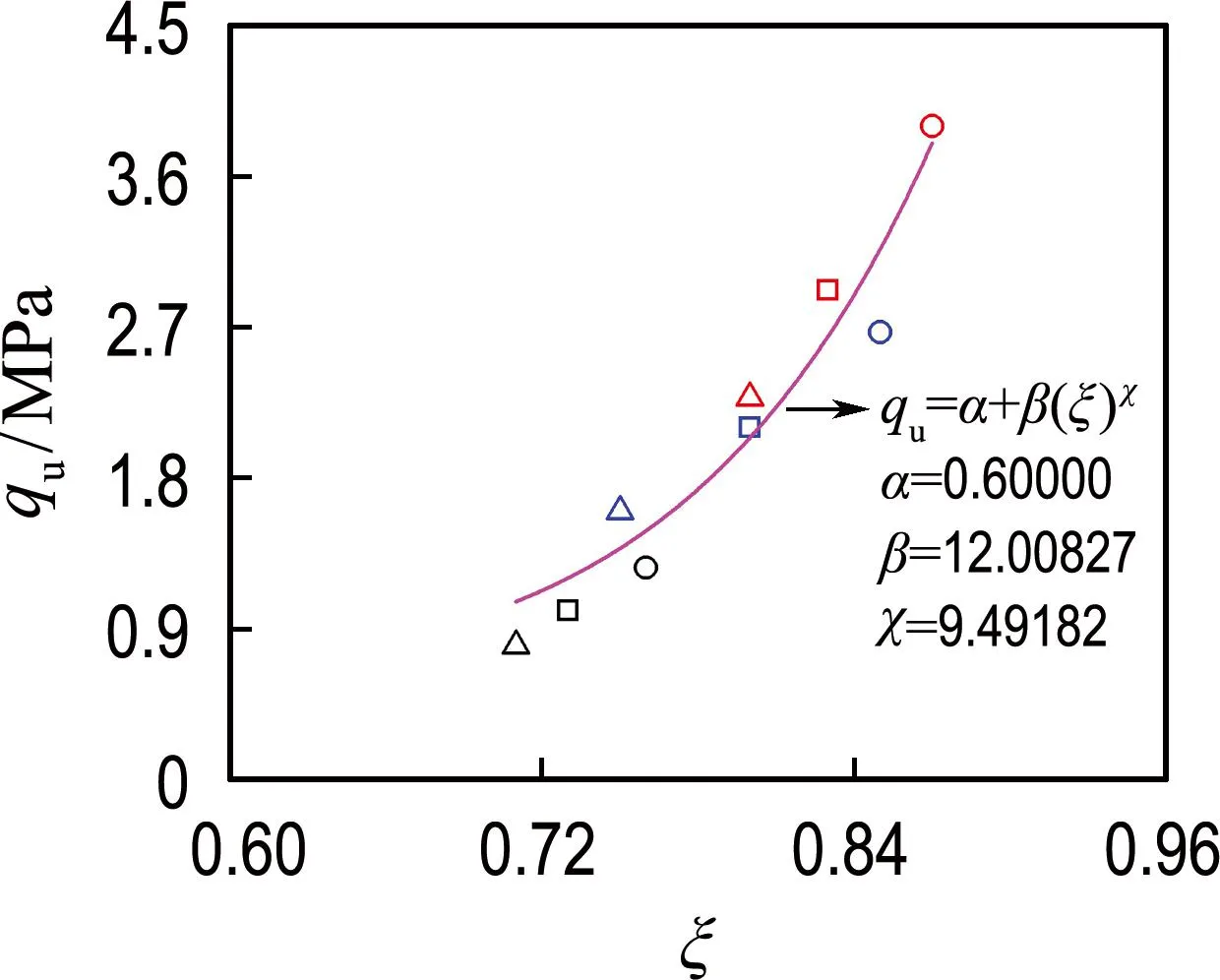
(b) 100 kPa围压
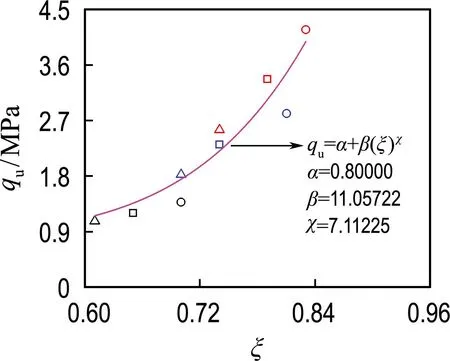
(c) 200 kPa围压

图12 峰值应力随相对结构度的变化
4 结 论
(1)建立了适用于水泥固化压实土的相对结构度发展式,该发展式给出相对结构度与塑性体应变的关系,其中的材料参数只与水泥掺量有关,而与试样的初始孔隙比无关,即增大初始孔隙比虽然会弱化土体结构性,使得试样更容易被破坏,但初始孔隙比并不影响试样在变形过程中相对结构度随塑性体应变发展的衰变速率.
(2)胶结强度、初始孔隙比和围压决定了土体结构的完整程度,是决定应力-应变曲线形态的关键因素.胶结作用会强化土体结构,而增大初始孔隙比会弱化胶结作用的影响.在相同荷载下,相对结构度随着水泥掺量的增加而增大,使得水泥固化压实土易于出现应变软化现象,但其随着初始孔隙比的增大而减小,使得水泥固化压实土易于出现应变硬化现象.
(3)水泥固化压实土试样的峰值应力与试样的相对结构度有关,其值随着相对结构度的降低而减小,并与相对结构度呈幂函数关系,与相对结构度有关的材料参数随着围压的增大而减小,即相对结构度对峰值应力的影响随着围压的升高而降低.

