基于两相流欧拉方法的中空纤维管血流动力学数值模拟
朱 桥 辉, 许 少 锋, 王 子 恒, 陆 俊 杰, 张 学 昌
(1.浙江大学 机械工程学院, 浙江 杭州 310027;2.浙大宁波理工学院 机电与能源工程学院, 浙江 宁波 315100;3.浙江理工大学 机械与自动控制学院, 浙江 杭州 310018 )
0 引 言
人工肝支持系统(artificial liver support system,ALSS)简称人工肝,可将人体血液引出至体外机械装置帮助净化人体血液内各种有害物质、改善血液内环境,暂时替代和辅助肝脏代谢、解毒等功能[1].人工肝在临床上可用于肝病重症、肝衰竭患者的相关治疗[2].在对危重症肺炎患者的治疗中[3],人工肝可用于清除炎症介质等有害物质,补充白蛋白等有益物质,从而阻断细胞因子风暴,帮助患者改善呼吸功能,减轻肺炎症状,提高危重症肺炎患者的救治率.中空纤维组件是人工肝的核心装置,其中有大量的中空纤维管,当血液流经中空纤维管时,血液内的有害物质通过中空纤维膜进入外腔,从而达到净化血液的目的,研究血液在中空纤维管内的流动行为对研究人工肝具有科学意义.
Baskurt等[4]的研究表明血液的表观黏度取决于现有的剪切力,并由红细胞比体积、血浆黏度、红细胞聚集和红细胞的力学特性决定.Shariatkhah等[5]使用非线性黏弹性模型研究了毛细血管中周期性发展的血流,并根据实验数据与Giesekus 模型推导出了流动因子和零剪切速率黏度的最佳值,结果表明只有非线性黏弹性模型才能准确描述毛细血管中血流的实验数据.Apostolidis等[6]研究了动脉血流动中的非牛顿血液流变学效应,结果显示采用牛顿模型与非牛顿模型描述血液黏度时模拟结果存在显著差异,这些差异主要归因于流动中低剪切速率区域和高剪切速率区域之间存在的耦合.Hund等[7]在Krieger悬浮液模型的基础上,提出了新的血液黏度模型,解决了先前模型在红细胞比体积和剪切速率方面表现出的不连续性问题.Wu等[8]使用混合理论模拟了微通道的血流,红细胞被建模为具有剪切依赖性黏度的非线性流体,并考虑了红细胞比体积的影响,结果显示在速度场和红细胞的体积分数分布方面与实验观察结果非常吻合.Marhefka等[9]对血液在微尺度流动进行了实验观察,结果显示血液在微管或小管(直径小于0.3 mm)内流动时在靠近管壁的地方会出现一层薄薄的血浆层,称为红细胞的耗竭层,在耗竭层下游的分支血管中会出现血浆撇渣效应,导致在较小的血管分支中红细胞的减少,可能会损害血液在远端毛细血管中氧气的运输.其他学者还发现了Fåhræus-Lindqvist效应、塞子流等现象[10].
血液的微观流动已经得到了大量研究,但对血液中红细胞受力的作用机理和迁移规律的研究还远远不够.为了真实反映出人工肝中空纤维管内的血流动力学和红细胞迁移规律,本文对中空纤维管内血液两相流动进行三维数值模拟,构建中空纤维管的三维模型,采用欧拉双流体模型,并使用用户自定义函数(UDF)描述红细胞升力方程,模拟人工肝中空纤维管内血液的流动情况,讨论壁面升力作用对红细胞径向移动的影响,分析中空纤维管内血液两相流体的速度分布、红细胞径向体积分数分布、黏度分布以及壁面条件对红细胞体积分数分布的影响,并根据相关数值结果分析红细胞所受升力的作用机理.研究结果旨在探讨人工肝内血液微观流动行为规律,以期为中空纤维组件的选材与优化设计提供一定的理论指导,提高研发效率,节约研发成本.
1 模型建立
1.1 数值模型
人体血液是由红细胞、白细胞、血小板、血浆等组成的混合流体,血液中红细胞与血浆的比例大于0.99,而白细胞与血小板所占比例不到0.01,一般忽略不计.因此血液被看作红细胞与血浆组成的两相系统,其中血浆在血液内的体积分数εp=0.55,红细胞在血液内的体积分数εRBC=0.45[11].对血液流动模拟计算时,血浆被看作液相,红细胞被看作颗粒相(固相),由于红细胞的体积分数较高,可将颗粒相红细胞假设为拟流体,模拟采用的两相流模型为欧拉双流体液-固两相流模型.
1.1.1 血液两相流基本方程 采用欧拉双流体模型,各相均可用统一的质量和动量守恒方程描述.质量守恒方程[12]为
(1)
式中:k为p或RBC,p、RBC分别代表血浆与红细胞;ρ为密度;ε为体积分数;v为速度矢量.血浆和红细胞体积分数之和恒为1,可表示为
(2)
动量守恒方程[12]为

(3)
式中:p为流场压力,τk为应力张量,Fk为虚拟质量力、浮升力等力源项,β为相间动量交换系数,g为重力.
1.1.2 本构方程 为使上述基本方程组封闭,需给出密度、黏度等参数对应的本构方程.混合密度ρmix是由血浆和红细胞的密度按其所占的体积分数加权计算得到,表达式为
(4)
1.1.3 血液黏度模型 血液黏度模型是模拟血液动力学流动的关键因素.非牛顿剪切稀化模型能够描述中性稠密浮力悬浮液中高体积分数颗粒的流动.采用Carreau-Yasuda模型来模拟血液流动的非牛顿特性,血液黏度会随着红细胞体积分数和剪切速率的变化而变化,根据人体血液的实验流变学数据,计算得到混合物的具体量纲一黏度表达式[13-14]为
(5)

(6)
(7)
正常生理条件下,血浆是牛顿流体,血浆黏度[16]为0.001 2 kg/(m·s),而红细胞黏度会随其体积分数的变化而变化,呈现出剪切稀化特性[17].
液相(血浆)应力张量以牛顿形式表示,本构方程为
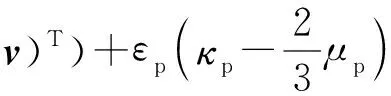
(8)
式中:κp表示血浆的体积黏度,I表示单位应力张量.一般条件下,血浆的体积黏度κp设为0.
固相(红细胞)应力张量的本构方程[18]为
τRBC=-pRBCδ+εRBCμRBC(∇v+(∇v)T)+

(9)
式中:δ表示Kronecker函数;pRBC表示红细胞颗粒间因发生相互碰撞、排斥作用而产生的压力,由于红细胞的比体积范围内颗粒间产生的压力微乎其微,可忽略不计;κRBC表示红细胞的体积黏度,其数值为0;红细胞黏度μRBC采用Carreau-Yasuda模型计算得到.
1.1.4 曳力系数 颗粒相与液相(血浆)之间的曳力采用Schiller-Naumann模型来表示相间动量交换系数β,其表达式[12]为
(10)
其中曳力系数Cd表达式为
(11)
(12)
式中:dRBC表示红细胞颗粒的直径,φ表示形状因子.红细胞颗粒的直径被假定为8 μm,由于不考虑红细胞变形影响,其形状因子φ为1[15].
1.1.5 虚拟质量力 当加速的颗粒相与液相(血浆)发生碰撞时,由于具有一定惯性作用,颗粒相会受到虚拟质量力,其表达式[19]为
(13)
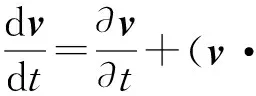
1.1.6 升力方程 受限剪切流场中,在壁面条件和径向速度梯度的作用下,考虑到红细胞变形作用[20],红细胞会受到经过其轴心的非惯性升力作用[21-22],该作用力会导致红细胞发生流场内的径向运动,对血液的流场分布、红细胞的径向分布、壁面剪切力产生影响.
两相流模型中红细胞所受的非惯性升力作用,当红细胞的轴心距离壁面小于5 μm时,升力作用由壁面条件决定;当红细胞的轴心距离壁面大于5 μm时,升力作用由剪切流场中的速度梯度引起,其表达式[22-23]为
(14)
式中:U表示量纲一滑移速度,与红细胞内部、外部流体黏度比有关,在本式中U恒为常数,即U=0.03[19,24];h表示红细胞轴心与壁面的距离;f(s)是以s为自变量的量纲一函数[25-26],s是指与红细胞具有相同表面积的球体相比红细胞的减少量,假设红细胞在h=5 μm处不再和壁面发生接触,由壁面条件所引起的升力[25-26]为0,并假设f(s)随着h呈线性变化,当h=0 μm时,f(s)=2;当h=5 μm时,f(s)=0.
1.2 几何模型与求解设置
由于1.1节中用于血液流动模拟的两相流数学模型比较复杂,在模拟中空纤维管内血液流动时,为了降低数值求解过程对计算机性能的要求以及相关计算参数的求解,中空纤维管模型采用三维轴对称结构,模型示意图如图1所示,中空纤维管截面直径Ф为100 μm,长度L为5 mm.

图1 中空纤维管模型示意图
采用ANSYS ICEM 2020R2对三维结构离散化,模型网格划分采用六面体网格法,为准确模拟血液在壁面附近的流动情况,通过对壁面边界层进行加密,共设置了11个边界层.其中,模拟时设置了3种不同网格数量的中空纤维管模型进行数值求解,并选用距入口0.5L截面处的红细胞径向体积分数分布结果进行比较,表1给出了不同网格数量模型下的红细胞在壁面邻近处的最大体积分数比较.由表1可知,不同网格数量模型下红细胞在壁面邻近处的最大体积分数存在差异,网格数量为80 735的模型与网格数量为200 901的模型计算结果相差3.404%,而网格数量为200 901的模型与网格数量为429 600的模型计算结果相差0.488%.因此在保证计算效率和计算精度的前提下,本文选用网格数量为200 901的模型进行数值求解.

表1 不同网格数量模型下红细胞在距入口0.5L截面处的最大体积分数比较
模拟时血液混合密度为1 059.7 kg/m3.血浆密度为1 030 kg/m3,黏度为0.001 2 kg/(m·s).红细胞颗粒的直径为8 μm,密度为1 096 kg/m3.红细胞的体积分数在入口处恒有εRBC=0.45,液相(血浆)和固相(红细胞)在入口处保持相同速度,模拟过程中流速始终保持不变,均为0.2 m/s.出口边界条件设置为开放出口,相对压强为0.根据中空纤维管直径与血液流速,计算得到平均雷诺数Re为17.66,可看作层流状态.使用计算流体模拟软件ANSYS FLUENT 2020R2进行模拟,迭代计算采用经典相间耦合Simple算法.
2 结果与讨论
2.1 血液两相流体的速度分布
对中空纤维管内血液两相流体的速度分布特性进行分析,在流场作用下,入口边界条件对血液各相沿径向速度分布的影响较小,模拟发现距入口不同位置处,血液两相流体沿径向速度分布曲线基本相同.图2给出了红细胞在距入口0.5L截面处的速度分布.由图2可知,中空纤维管轴心处速度最大,管壁处速度为0,符合层流流动特性.根据图2的相关结果,图3给出了红细胞和血浆在距入口0.5L截面处的速度分布曲线,同时给出了将血液作为单相牛顿流体的速度分布曲线,横坐标r/r0表示量纲一半径,r表示红细胞或血浆与管内中心的距离,r0表示中空纤维管半

图2 红细胞在距入口0.5L截面处的速度分布
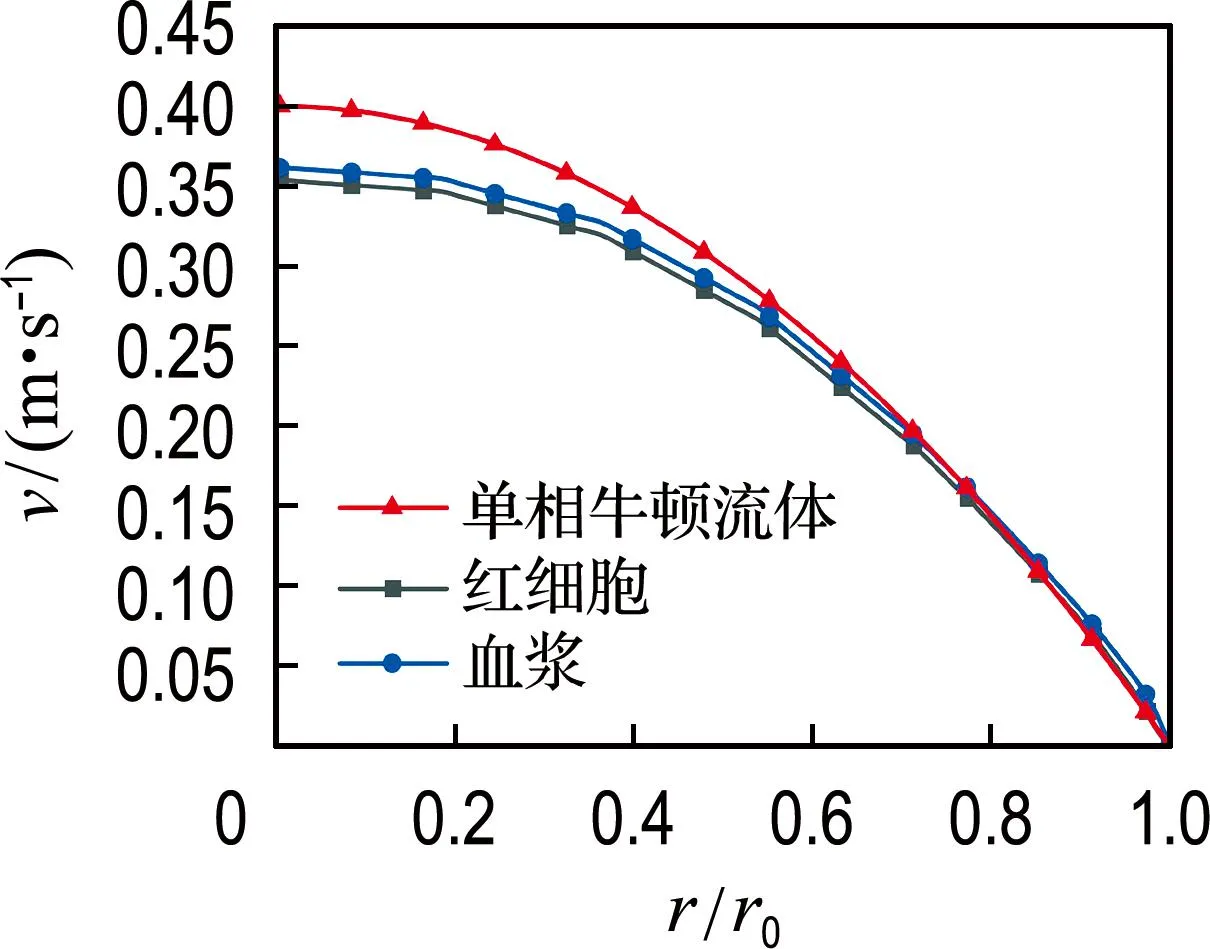
图3 中空纤维管内血液两相流体沿径向速度
径.由图3可知,血液各相的速度呈近似抛物线分布,各相在中空纤维管轴心上的流速大于壁面流速,但血液两相流模型中血液各相的速度小于血液流动(单相牛顿流体)所形成的抛物线速度.血液表现出一定的非牛顿特性,由于颗粒相红细胞的存在,颗粒相会拖曳液相(血浆)的流动,减缓其流动速度.其中,径向各位置处红细胞流动速度略小于血浆流动速度,该结果与Chandran等[27]采用扩散通量模型得到的研究结论一致.
2.2 红细胞径向体积分数分布
对中空纤维管内红细胞在距入口不同位置处沿径向的体积分数分布进行统计,共选取了3个截面,其位置与入口的距离分别为0.2L、0.5L、0.8L,图4给出了红细胞在距入口0.5L截面处沿径向的体积分数分布.结果显示,在径向上,红细胞在壁面处受壁面产生的升力作用较大,红细胞远离壁面.与入口处红细胞体积分数εRBC=0.45相比,壁面处红细胞体积分数减小并小于入口处
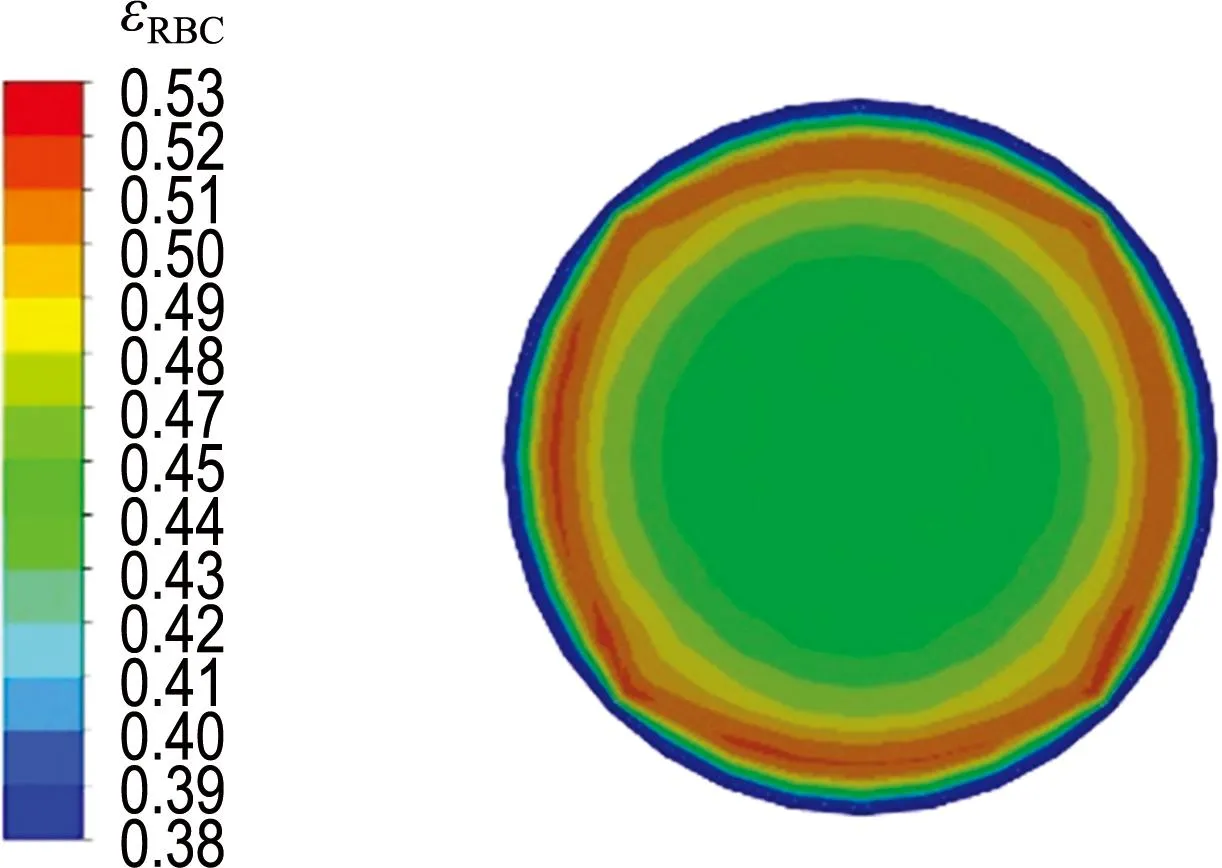
图4 在距入口0.5L截面处红细胞沿径向的体积分数分布
红细胞体积分数,说明红细胞向远离壁面的方向发生迁移,与Geislinger等[28]的研究结论相符.在邻近壁面处(距离壁面一定距离处),红细胞所受的壁面升力作用与流场剪切梯度对红细胞产生的升力作用两者相互平衡[21],此时红细胞体积分数出现最大值并高于入口处红细胞体积分数.在管内轴心附近处,红细胞体积分数略小于入口处红细胞体积分数.
根据不同截面上红细胞径向体积分数分布结果,图5给出了红细胞在不同截面上沿径向的体积分数分布曲线.结果显示,在管内轴心附近,红细胞体积分数略小于入口处红细胞体积分数,而在邻近壁面处出现最大值,红细胞沿径向体积分数分布呈双峰状.从邻近壁面处至管内轴心处,红细胞体积分数由最大值逐渐减小至局部最小值;而从邻近壁面处至壁面处,红细胞体积分数急剧减小.除此之外,对比各截面上红细胞在邻近壁面处的体积分数分布情况,距入口0.2L截面上,红细胞体积分数的最大值比其他两个截面上的最大值大,随着各截面与入口距离的增加,各截面上红细胞体积分数最大值逐渐减小;而在壁面处,随着截面与入口距离增加,红细胞体积分数逐渐增大,距入口0.8L截面上红细胞体积分数最大.
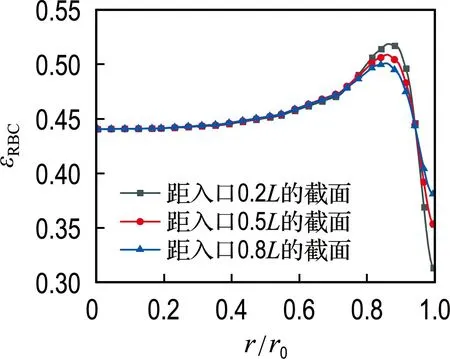
图5 红细胞在不同截面上沿径向的体积分数分布曲线
2.3 黏度分布
采用血液两相流模型模拟时,颗粒相红细胞被看作拟流体,模拟过程采用Carreau-Yasuda黏度模型描述红细胞黏度.图6给出了红细胞在距入口0.5L截面处的黏度分布.红细胞在壁面处流动速度小,速度梯度大,红细胞黏度低;在轴心附近处流动速度大,速度梯度小,红细胞黏度高.根据图6的黏度分布结果,图7给出了血液两相流体沿径向各位置处的黏度分布曲线.由图7可知,红细胞呈现出非牛顿特性,具有一定的剪切稀化特性.红细胞沿径向黏度变化最大,由于血浆是一种牛顿流体,其黏度不随体积分数与流速的变化而变化,模拟过程中黏度始终保持不变.血液主要是由红细胞与血浆组成的混合溶液,即血液由牛顿流体与非牛顿流体混合而成,整体上表现出一定的非牛顿特性,血液黏度会随红细胞体积分数与剪切速率的变化而变化.
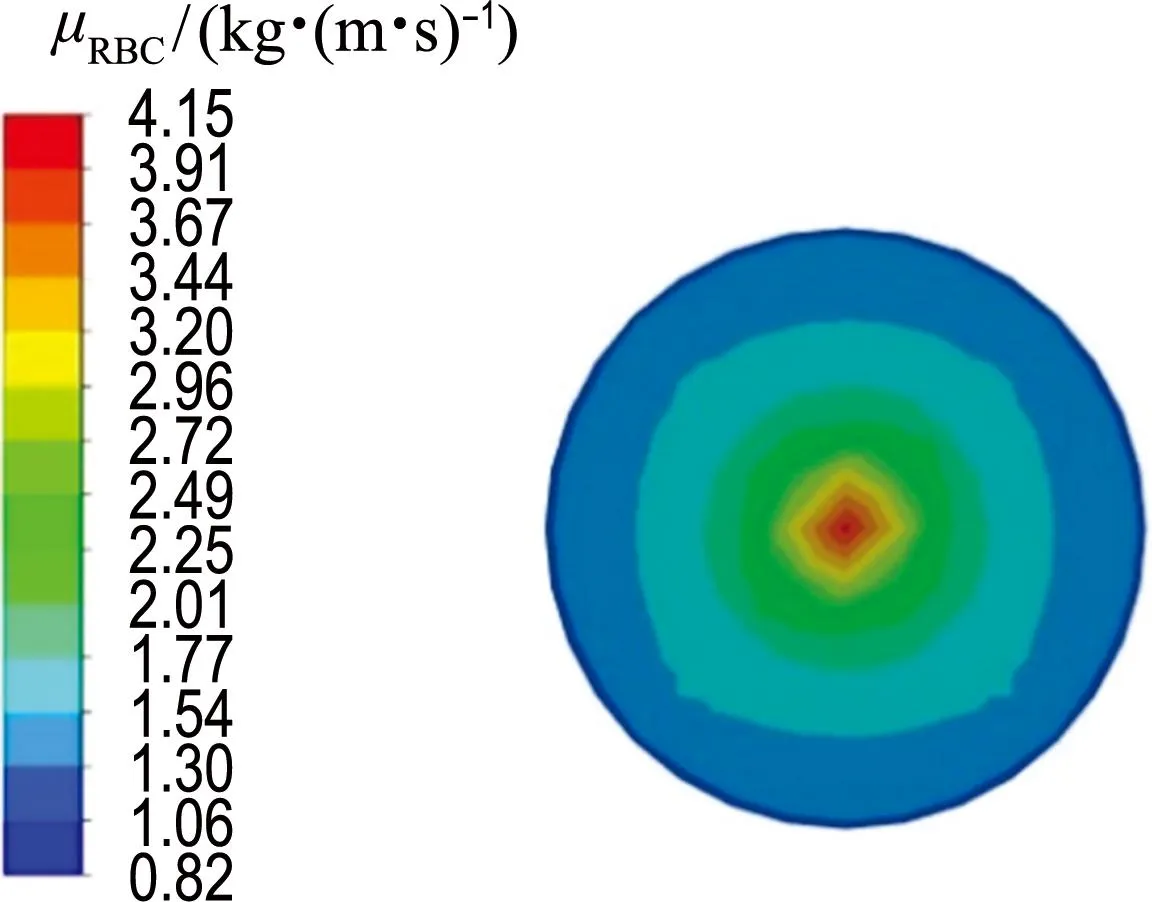
图6 红细胞在距入口0.5L截面处的黏度分布
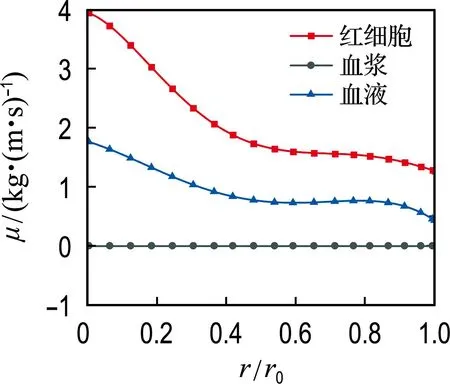
图7 血液各相沿径向的黏度分布曲线
2.4 壁面条件对红细胞体积分数分布的影响
由2.2节可知,红细胞在各截面沿径向的体积分数分布受到壁面升力作用以及血液流动对其产生的流体力学作用的影响.根据Wu等[8]的相关研究,壁面对囊泡状物体的升力会受到壁面剪切速率与囊泡变形作用两者共同的影响.为了分析红细胞在不同壁面条件下所受升力作用对其体积分数分布的影响,本节共设置了3组红细胞轴心与壁面距离h=0 μm时的f(s),以模拟血液在中空纤维管不同壁面弹性条件下的流动情况.假设f(s)随着红细胞距壁面的距离h呈线性变化,f(s)越小表征壁面所产生的壁面剪切速率对红细胞的变形作用越小时,即当红细胞距壁面的距离越小,受到来自壁面对红细胞产生的非惯性升力越大.图8给出了不同壁面条件下红细胞在距入口0.5L截面处沿径向体积分数分布曲线.由图8可知,随着壁面处的剪切速率与壁面对红细胞的变形作用越来越小(即壁面处f(s)越来越小),红细胞在邻近壁面处的体积分数逐渐降低,而在壁面处的体积分数越来越高,表明红细胞远离壁面的趋势减弱.
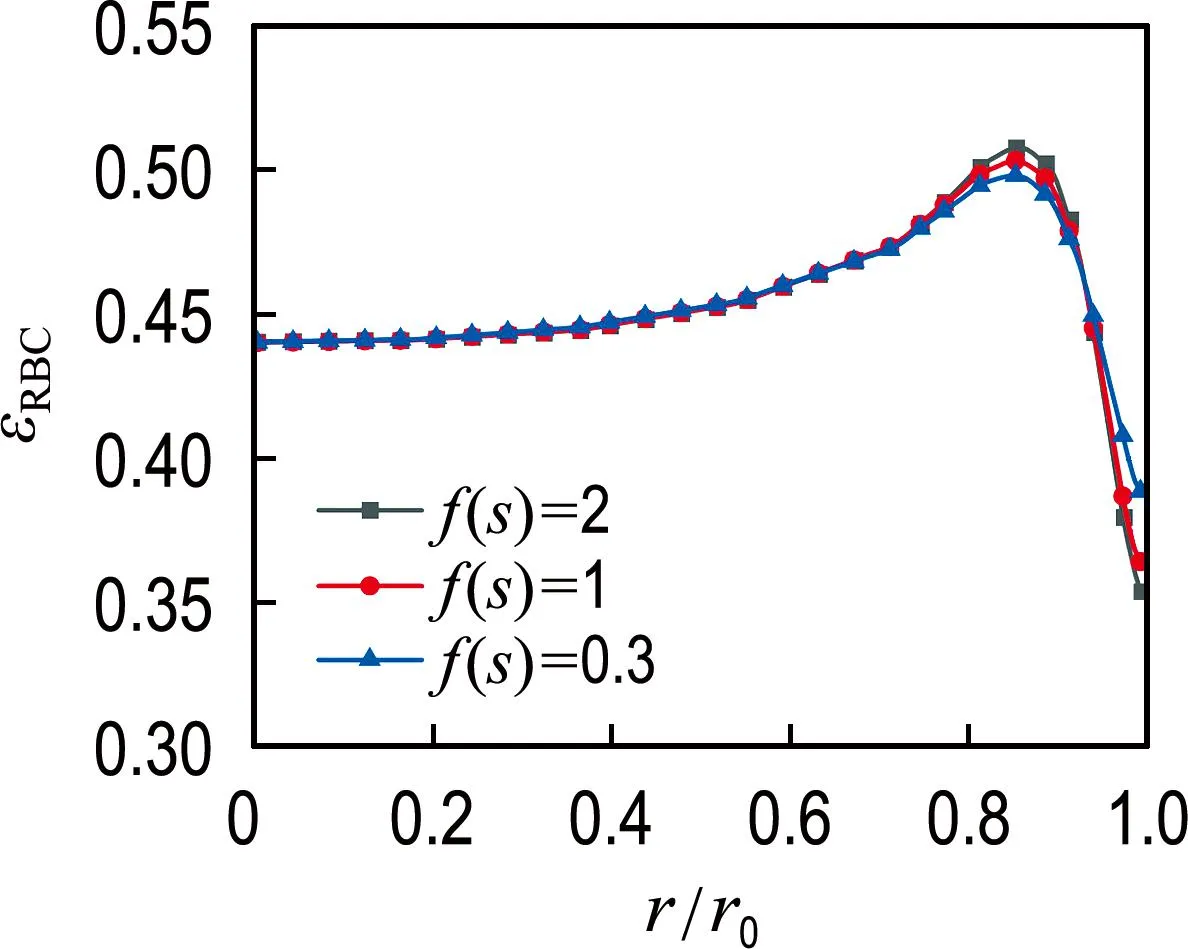
图8 不同壁面条件下红细胞在距入口0.5L截面处沿径向体积分数分布曲线
为了说明非惯性升力对红细胞径向迁移的影响,图9给出了红细胞在径向上的迁移机理示意图,图中Fl表示壁面对红细胞产生的非惯性升力,Fs表示流场剪切梯度对红细胞产生的升力.如图所示,当红细胞在壁面处时,所受的升力Fl>Fs,此时红细胞远离壁面;当红细胞在远离壁面处于管内中心线附近时,主要受流场剪切梯度产生的升力Fs,此时红细胞有沿径向向壁面迁移的趋势;当红细胞在紧邻壁面处(离壁面距离约为5 μm)时,红细胞受到的非惯性升力与剪切梯度产生的升力两者达到平衡,即Fl=Fs,此时红细胞会在邻近壁面处积聚,在该处红细胞体积分数出现最大值.当壁面处对应的f(s)减小时,红细胞在壁面处受到的非惯性升力Fl变小,导致径向上红细胞向管内中心的迁移趋势减弱,红细胞在邻近壁面处积聚程度下降,因此红细胞在壁面处的体积分数增大.该结果与Abkarian等[25]模拟的数值结果吻合.
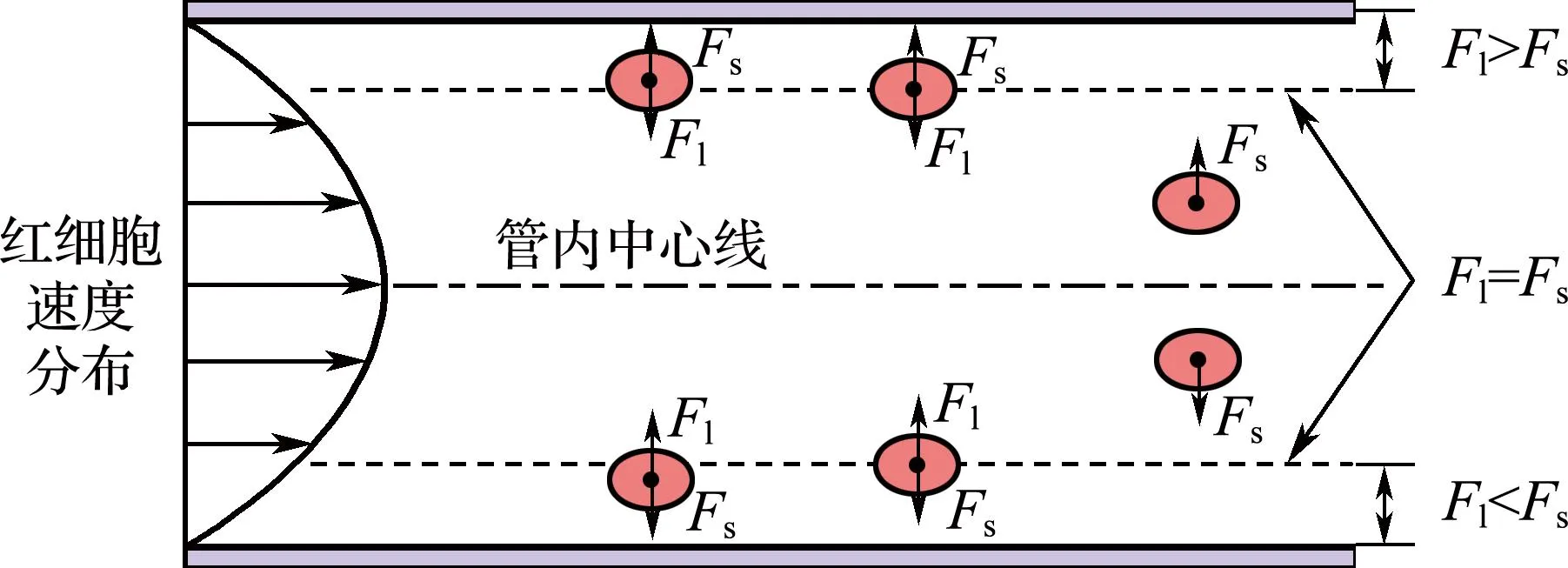
图9 红细胞所受非惯性升力与剪切梯度产生的升力作用机理示意图
3 结 论
(1)在层流流场作用下,血液中红细胞与血浆的流速呈近似抛物线分布,各相在轴心处流速均大于在壁面处流速,两相流体速度小于血液单相流动形成的抛物线速度,沿径向各位置处的红细胞流速略大于血浆流速.
(2)红细胞黏度会随体积分数与剪切速率变化而变化,壁面处速度梯度大,红细胞黏度低;轴心附近处速度梯度小,红细胞黏度高,血液整体上表现出非牛顿特性,呈现剪切稀化特性.
(3)红细胞在中空纤维管内流动时,壁面对红细胞产生升力作用,使得红细胞远离壁面,在距离壁面一定位置处,红细胞所受壁面升力作用与流场产生的流体力学作用达到平衡,红细胞体积分数在该位置处出现最大值.随着截面与入口距离的增加,该截面处红细胞体积分数最大值逐渐减小,在壁面处红细胞体积分数则逐渐增大.整体上看,红细胞沿径向体积分数分布呈双峰状.
(4)壁面对红细胞的升力作用会对红细胞沿径向体积分数分布产生影响,随壁面处剪切速率与壁面对红细胞变形作用的减小,红细胞在距离壁面一定位置处的体积分数减小,而在壁面处的体积分数增大,红细胞由壁面向管内中心运动的趋势减弱.
本文采用两相流欧拉方法描述了真实条件下血液在微观尺度下的流动规律,准确设置了血液两相流体的黏度模型、曳力模型、红细胞升力方程,相关参数根据表达式使用UDF描述.但由于本文主要采用升力方程来模拟红细胞在流动时的受力以反映管壁对红细胞迁移的影响,后续相关研究还可通过设置中空纤维管弹性条件,采用流固耦合等方法来模拟管壁对血液流动的影响.

