Z形折叠翼厚度对其气动特性影响分析

张 昊 哲, 段 富 海

(大连理工大学 机械工程学院, 辽宁 大连 116024 )

0 引 言

变体飞行器是一种新型的概念飞行器,它集新型智能材料、作动器、传感器于一体,通过大范围改变机翼面积、弯度、厚度、后掠角等参数,以满足起降、巡航、盘旋侦察、对地攻击等不同飞行任务的要求[1-3]．变体飞行器在性能上要求能够连续、光滑、大尺度、多自由度地主动变形,从而在执行多种任务时保持最佳气动性能[4]．折叠翼飞行器概念被洛克希德·马丁公司首次提出[5],其可在展开与折叠两种模式下切换,实现从远程巡航转换为高速冲刺杀伤,最终转换回远程巡航返回基地．折叠翼飞行器采用柔性蒙皮和智能材料作动器来实现折叠角为0°～130°的Z字形折叠,折叠过程中外翼与机身始终保持平行,机翼的面积变化量最大可达200%．

与传统的固定翼飞行器不同,折叠翼飞行器在折叠变形过程中,其机翼面积、重心和气动焦点等会发生变化,导致作用在飞行器上的气动力发生变化,这将影响飞行器的运动和稳定性．对此,Yue等建立了折叠翼飞行器折叠过程中的多体动力学模型,通过简化六体自由度非线性方程得到了解耦纵向动力学方程[6-7]．随后宋慧心等基于Kane方法建立了折叠翼飞行器的动力学模型,通过气动计算拟合了气动参数与折叠角的关系,分析了折叠过程中的动态特性[8]．Jung等利用非定常涡格法计算了折叠翼在折叠过程中亚声速流动的气动特性变化,分析了后缘面的尾迹位置随折叠角和折叠角速度的变化规律[9]．Tang等将折叠翼结构采用线性板理论进行理论建模,然后采用三维时域涡格气动模型研究了线性气动弹性系统的稳定性[10]．研究表明内外侧机翼扭转刚度的增加,将分别导致机翼气动弹性稳定性(颤振速度)的增加和降低,且折叠角对临界颤振速度也会产生影响．Li等由非线性结构方程和非定常气动力积分推导出折叠翼的气动弹性方程,并发现当折叠翼中存在一定范围的自由间隙时,系统可近似被视为线性系统[11]．

以上研究结果是基于升力面理论的,该理论认为流场绕机翼流动产生的气动力为弯度、厚度、攻角的线性叠加．厚度引起的绕机翼流动与机翼对称,不会对机翼的气动特性产生影响,因此忽略了厚度项．然而,在实际折叠翼折叠变形过程中,由于机翼存在厚度,机翼表面之间相互靠近产生强烈的气动干扰,会对折叠翼的升力、阻力、俯仰力矩和折叠铰链力矩等产生严重影响,所以升力面法并不能完全准确地计算折叠翼的气动特性,忽略厚度项带来的偏差也有待研究．为此本文首先利用薄翼理论和升力面法推导理想气体来流条件下折叠翼的定常气动力表达式;然后采用CFD法对机翼的折叠进行模拟,分析计算折叠翼气动特性及机翼厚度引发低压区的强度变化;最后将CFD法结果与升力面法结果进行对比,分析厚度项在机翼折叠过程中对机翼升力、折叠铰链力矩变化的影响．

1 Z形折叠翼模型

Z形折叠翼可看作是一个柔性多体结构,由3个部分构成：Ⅰ机身、Ⅱ内翼、Ⅲ外翼,如图1所示为折叠翼右侧半模型．机翼折叠过程中,内翼沿机身轴线方向向内转动,外翼与机身时刻保持平行,折叠角为θ．整机采用柔性蒙皮,折叠处用铰链连接,采用CLARKY翼型,飞行高度3 km,机翼全展开与全折叠两种模式下飞行速度分别为0.2Ma和0.4Ma,最大折叠角为120°,机翼其他气动参数见表1．

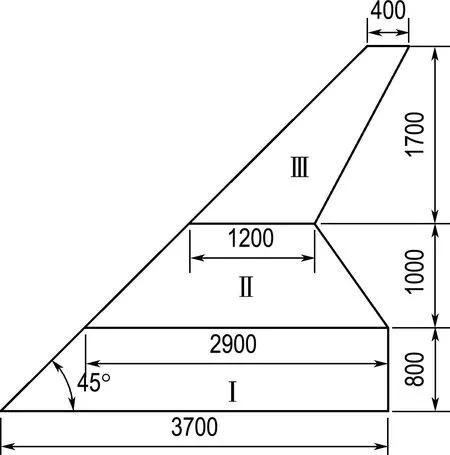
(a) 折叠翼尺寸

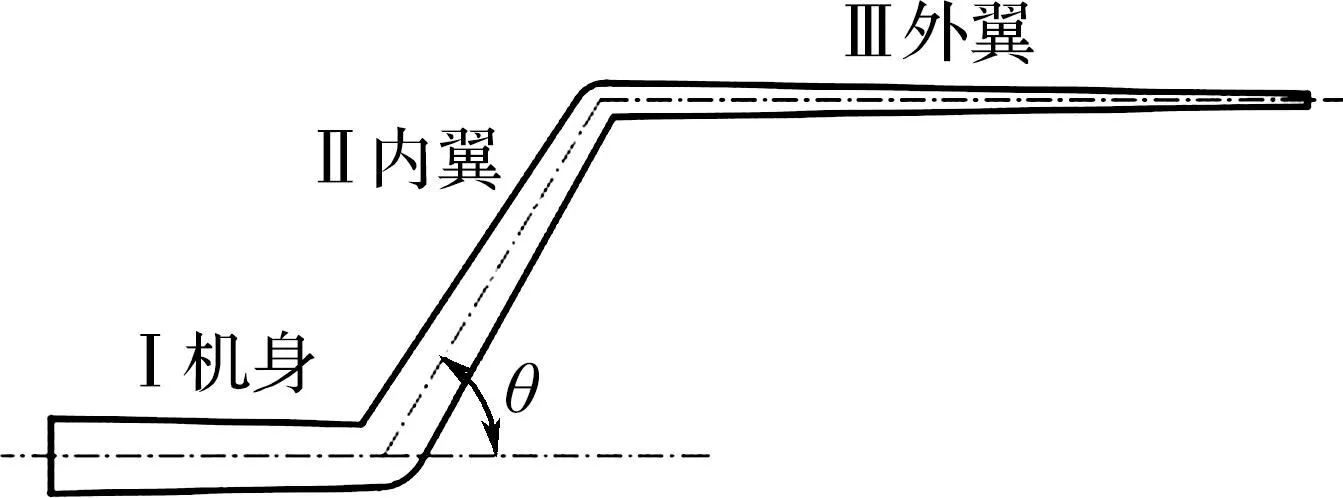
(b) 折叠角

表1 Z形折叠翼飞行器参数

2 Z形折叠翼气动力推导

本文分析的折叠翼飞行器气动特性是在亚声速飞行条件下,且CLARKY翼型最大厚度、最大弯度远小于弦长,满足薄翼理论对薄翼型的定义．假设飞行器周围的流体是无黏性、无旋转、不可压缩的理想气体,其流场为势流场,势函数满足拉普拉斯线性方程和叠加原理．因此,用一个沿中弧线连续分布的面涡代替薄翼型,由于翼型为薄翼型,可以用弦线上的面涡作为中弧线上面涡的近似,如图2所示．

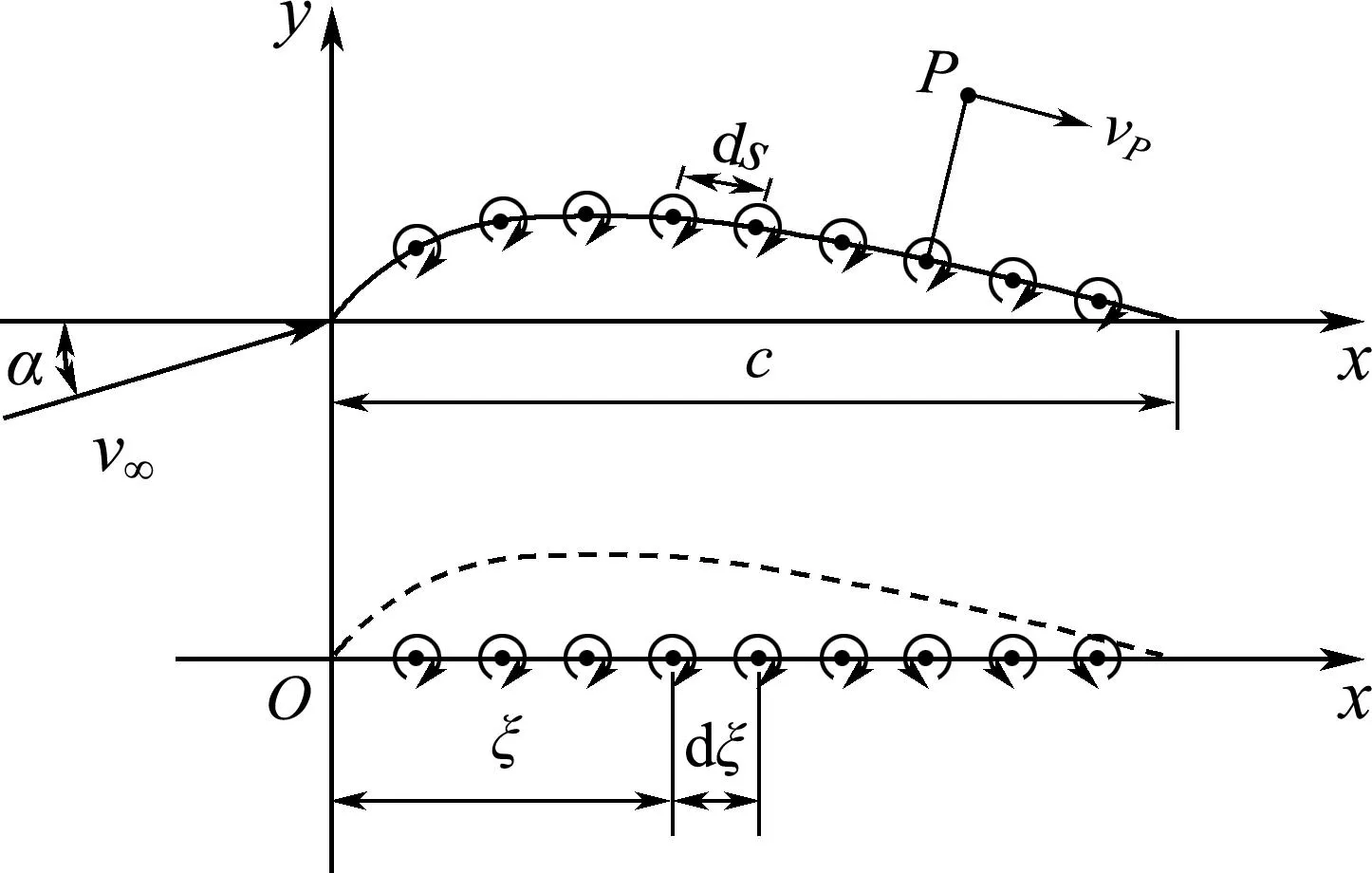
图2 中弧线上的面涡及诱导速度

图2中翼型的总环量为

(1)

由毕奥-萨伐尔公式,中弧线整个面涡在弦线上某点诱导的合速度为

(2)

假设气体光滑地流过机翼表面,且机翼表面大部分区域为附着流动,为使得均匀流动与涡诱导流动线性叠加后,面涡与中弧线重合,面涡上任意点处对应流场中某点P所产生的诱导速度的法向分量vPn与均匀流在点P处的法向速度v∞n叠加应等于零．即面涡上任意一点的诱导速度与均匀流速度的合速度与中弧线相切．因此边界条件可以表示为

(3)

将式(2)代入边界条件得

(4)

采用级数法对式(4)求解,令

(5)

将γ(ξ)表示为傅里叶级数γ(θ)：

(6)

其中A0,A1,…,An为待定系数．

由式(5)和式(6)计算得到

(7)

经计算得到翼型总环量表达式为

(8)

则翼型的升力表达式为

(9)

升力系数表达式为

(10)

根据文献[9],当折叠角速度小于30 rad/s时,非定常气动力效应对于飞行器的整体气动特性影响较小,可忽略不计,即机翼在折叠过程中任意时刻的气动特性只与该时刻的飞行状态和静态结构有关．因此可以用准定常假设对折叠翼的气动特性计算进行简化．将CLARKY翼型数据导入MATLAB求解翼型中弧线方程为

y=a+b1x+b2x2+b3x3

(11)

式中：a=-4.483 06×10-4,b1=0.187 35,b2=-0.287 64,b3=0.101 59．

将式(5)代入中弧线方程计算得到

(12)

则

(13)

A1=-b2-3b3

(14)

折叠翼单位翼展的升力为

(15)

折叠翼单位翼展的升力系数为

(16)

根据Z形折叠翼展开与折叠的运动过程,折叠角为θ,折叠角范围为0°～120°,推导得到折叠翼整体气动力表达式为

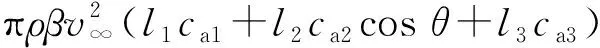
(17)

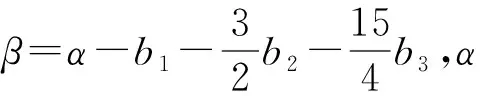
3 Z形折叠翼CFD法气动力分析

3.1 基于CFD法折叠翼的气动建模

本文采用Fluent Meshing软件对Z形折叠翼进行网格划分,其中折叠角在0°～120°,每15°划分一次网格,图3为折叠角为60°的折叠翼外场和其壁面网格分布,采用非结构化网格进行划分,最终得到约732×104个四面体单元．通过Fluent软件,采用SSTk-ω湍流模型,求解Euler方程模拟折叠翼周围的流动．

图3 折叠角为60°的模型壁面网格

3.2 低压区的形成

Z形折叠翼飞行器在折叠变形过程中,随着折叠角的增加,机翼表面彼此之间相互靠近,会产生气动干扰．图4为折叠翼在折叠角为120°,飞行速度为0.3Ma时机翼表面压力分布云图．图4显示在机身与内翼、内翼与外翼表面靠近折叠处产生了明显的低压区,当折叠角大于90°时这种气动干扰产生的低压区尤为明显．

(a) 内低压区

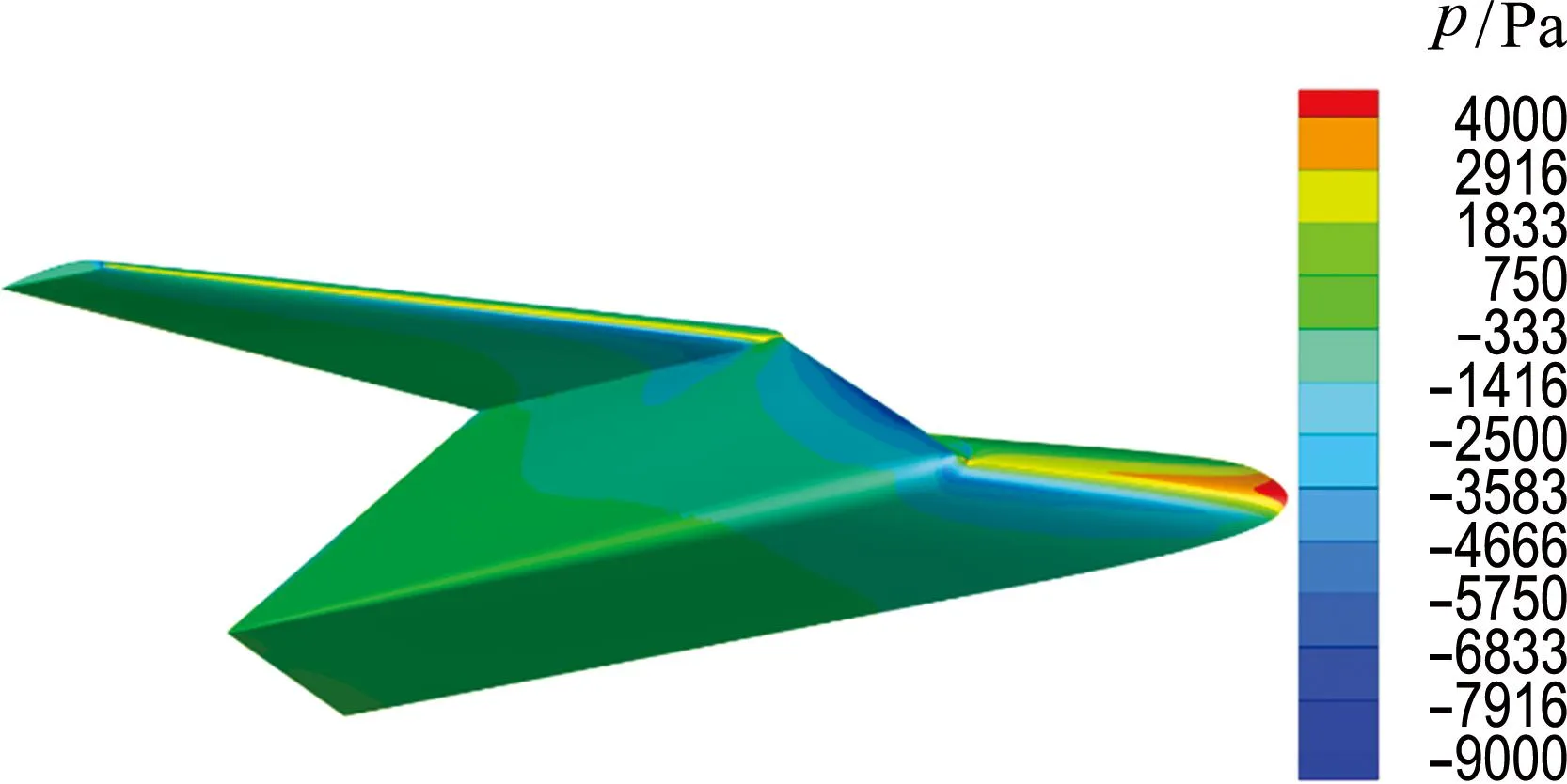
(b) 外低压区

低压区产生原因如图5所示,由于机翼存在厚度,机翼的上下表面为具有弯度的面,并非理想状态下的平直板,当机翼折叠角增加,机身与内翼的上表面、内翼与外翼的下表面相互靠近,形成两个狭窄的气流通道．当气流流经两个气流通道时,流速加快,形成两个低压区(内低压区、外低压区),并产生两个额外的气动荷载F1、F2．

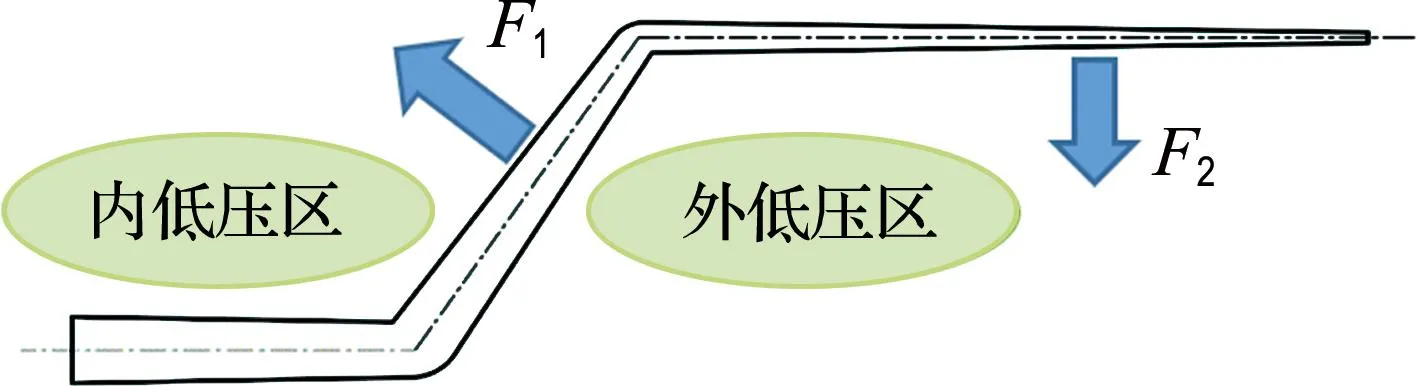
图5 低压区及气动荷载

图6显示了由内外低压区产生的气动荷载随折叠角的变化曲线,该变化表明,随着折叠角的增大,内外低压区的强度均增加,而且增加的程度逐渐增大,当折叠角大于90°时,内外低压区的强度增加尤其明显．其中内低压区的强度远高于外低压区的强度,产生此现象的原因有两个：一方面,机身与内翼之间所形成低压区的面积远大于内翼与外翼所形成低压区的面积,导致内低压区的气流加速通道更长;另一方面,本文折叠机翼选用的为CLARKY翼型,该翼型为平凸翼型,即机翼上表面弯曲,下表面平坦,导致机翼表面相互靠近时,机身与内翼上表面之间的夹角小于内翼与外翼下表面之间的夹角,内低压区的气流通道相较于外低压区更狭窄．因此,在机翼折叠过程中,所产生的内低压区的强度远大于外低压区的强度．

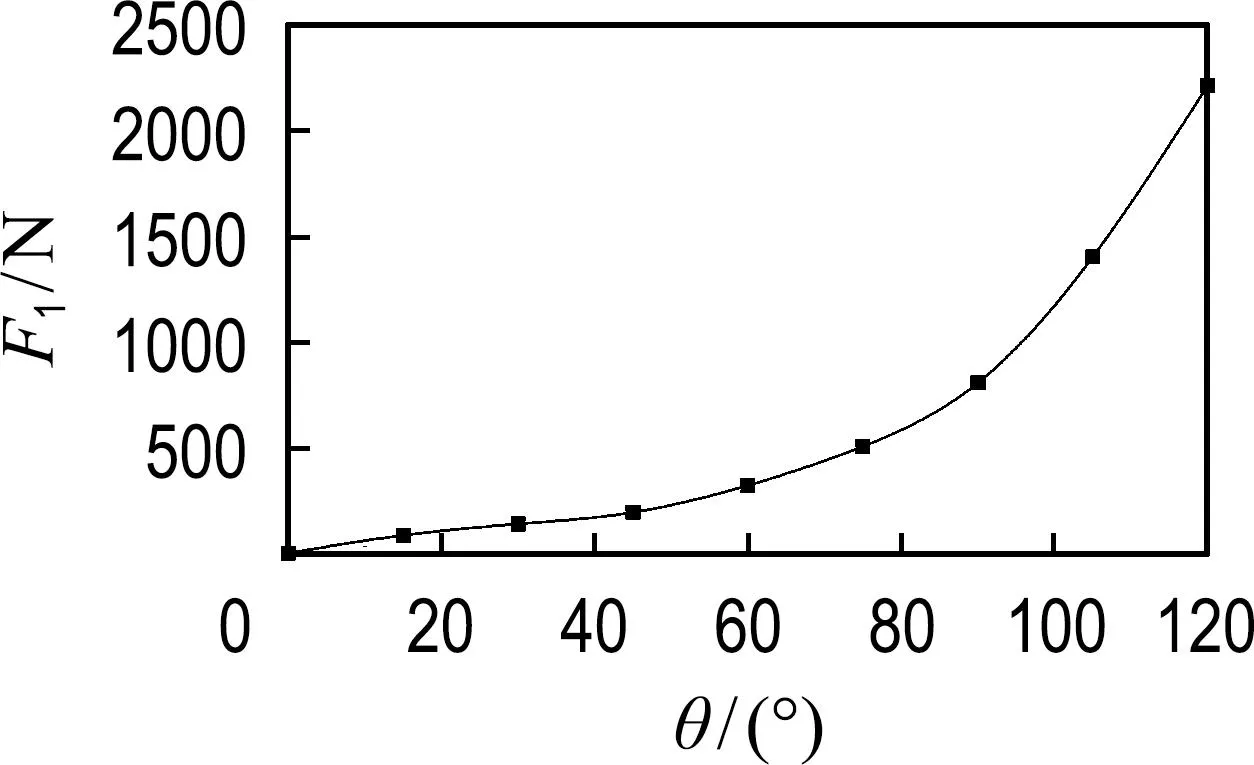
(a) F1

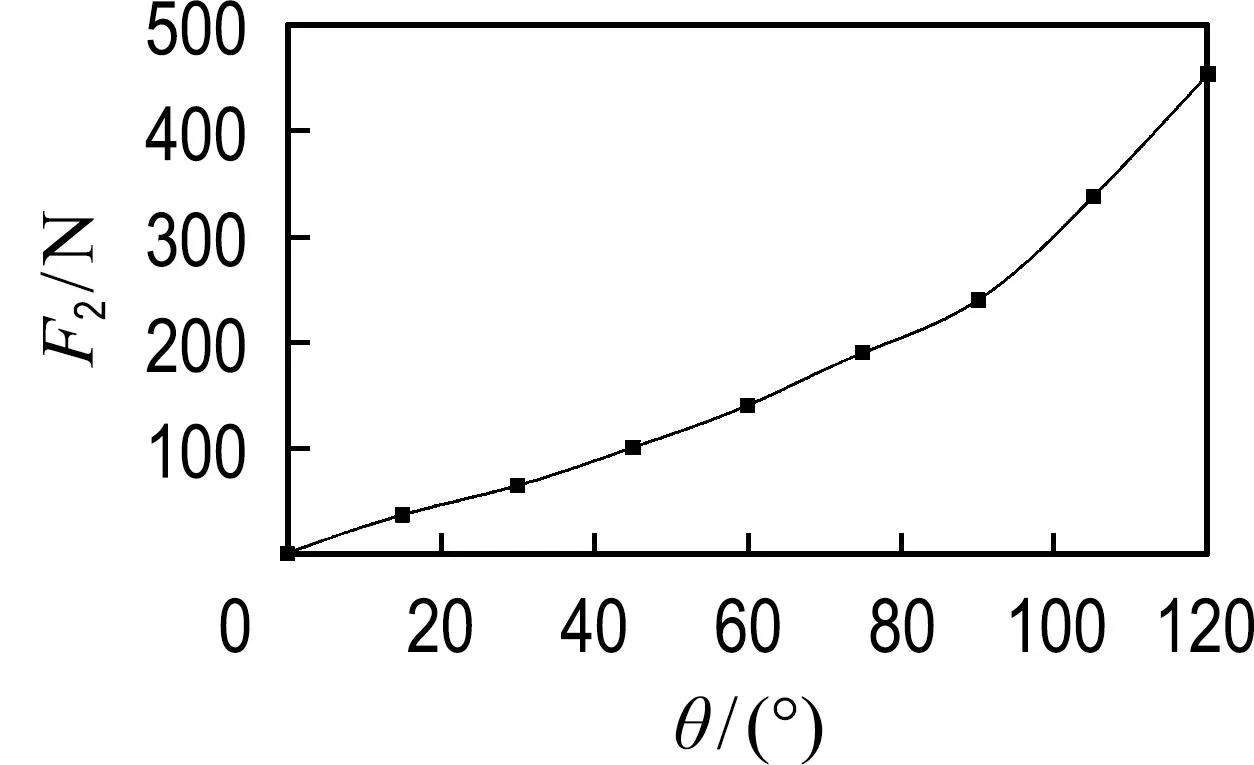
(b) F2

3.3 基于CFD法的模拟结果分析

折叠翼在全展开和全折叠状态下,分别用于执行低速巡航和高速突防的不同飞行任务,而且在实际的飞行和折叠过程中飞行速度也是变化的．但由于这涉及较为复杂的流动参数变化,飞行速度与机翼折叠角的对应匹配也有待研究,不利于计算结果的比对分析,因此本文只考虑固定飞行速度的情况．选取来流速度为0.3Ma,用CFD法分别计算攻角为1°、3°、5°、7°、9°条件下,机翼由全展开到折叠角为120°的升力、阻力系数和俯仰力矩系数变化,如图7所示．

由图7可见,在攻角、来流条件相同的条件下,机翼折叠过程中,随着折叠角的增加,机翼有效气动面积减小,机翼的升力和阻力系数均减小．当折叠角大于90°时,由于厚度效应产生的内外低压区强度增加,F1、F2大幅增加,使得机翼的升力、升力系数大幅下降．而且攻角越大,机翼在折叠过程中升力和阻力下降越明显．

(a) 升力

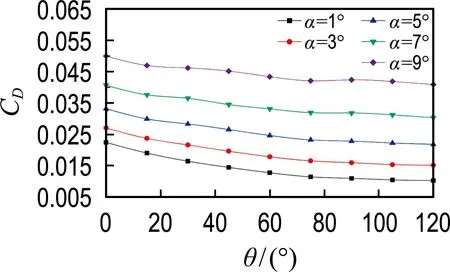
(b) 阻力系数

(c) 俯仰力矩系数

图7(c)显示随着折叠角增加,机翼的俯仰力矩系数绝对值增大．主要是由于机翼在折叠过程中气动焦点发生变化,如图8所示．气动焦点会随着机翼折叠、升力面后移从而向后移动,因此,机翼的低头俯仰力矩增加,稳定性降低．而且,随着机翼折叠角增加,机翼有效气动面积减小,升力降低,飞机的高度会下降,为了保持飞行高度和纵向稳定性,应控制副翼向上偏转,产生抬头俯仰力矩,增加攻角,提高升力．

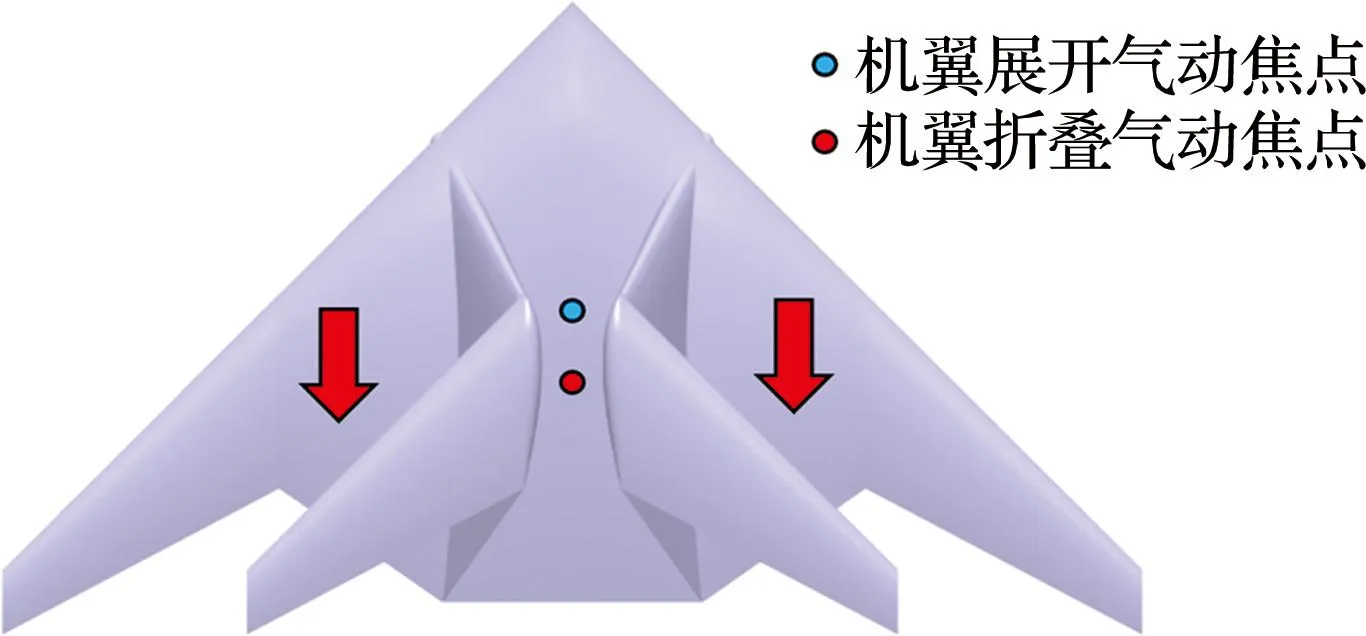
图8 机翼折叠气动焦点位置变化

用CFD法模拟计算,折叠翼在攻角为5°的飞行条件下,折叠过程中内外翼铰链力矩变化如图9所示．在机翼全展开时,内翼铰链受内外翼气动力共同影响,而外翼铰链只受外翼影响,因此在该状态下内翼铰链力矩较大,为4 558 N·m,外翼铰链力矩较小,为2 690 N·m．随着折叠角的增加,内翼铰链力矩先减小后增大,外翼铰链力矩持续减小,在机翼全折叠状态下内外翼铰链力矩分别为5 477 N·m和2 204 N·m．这是由于在机翼折叠过程中,作用在机翼上的气动力发生了几个重要变化．对于内翼铰链而言,首先,随着折叠角增加,作用在外翼上的气动力臂减小,而且由于折叠角较小,机翼厚度效应产生的内低压区强度较小,当折叠角小于60°时内翼铰链力矩呈下降趋势．随后,折叠角继续增加,厚度效应产生的内低压区强度大幅增加,导致内翼铰链力矩增大．对于外翼铰链而言,首先,当折叠角小于60°时,随着折叠角的增加,由机翼厚度效应产生的外低压区强度较小,所以外翼铰链力矩减小并不明显．随后,机翼继续折叠,外低压区强度明显增加,导致外翼铰链力矩大幅下降．

(a) 内翼铰链力矩

(b) 外翼铰链力矩

4 CFD法与升力面法结果分析对比

将Z形折叠翼在攻角为5°、飞行高度为3 km、飞行速度为0.3Ma的飞行条件下,折叠过程中的CFD法结果与升力面法结果进行比较．分析造成两种空气动力学模型获得的机翼升力、内外翼铰链力矩存在偏差的原因．

4.1 升力面法在Z形折叠翼气动力分析中的不足

升力面法是一种奇点分布求解线性化流势问题的方法,它被广泛应用于机翼和螺旋桨的空气动力学建模[12]．如图2所示,升力面法的核心思想是通过在机翼表面布置一些奇异点(源、汇、旋涡等)以代替绕流翼型,将三维问题简化为曲面问题求解,进而得到一些一般性的气动结论(升力、升力系数、力矩系数、压力中心、焦点等)．

对于固定翼飞行器,其流场为势流场,势函数满足拉普拉斯线性方程和叠加原理,所以在线性范围内,机翼的气动荷载可被认为是定常荷载和非定常荷载的线性叠加,而定常荷载在薄翼型、小扰动条件下可以视为弯度、厚度、攻角作用之和,如下式所示：

Cp=Cp,0+Cp,1=Cp,0,f+Cp,0,b+Cp,0,α+Cp,1

(18)

式中：Cp,0为机翼表面压强系数的定常部分,Cp,0,f为机翼弯度作用部分,Cp,0,b为机翼厚度作用部分,Cp,0,α为机翼攻角作用部分,Cp,1为机翼表面压强系数的非定常部分．

在求解升力问题时,升力面法认为其中的厚度项对升力不产生影响,因此将厚度项Cp,0,b省略,没有布置机翼厚度对气动特性影响的奇异点．因此,升力面法简化了固定翼飞行器的气动模型,并且目前为止仍广泛应用于常规固定翼飞行器的气动分析中．

对于Z形折叠翼飞行器而言,随着机翼折叠角的增加,机翼表面相互靠近,产生强烈的气动干扰并形成内外低压区,会对机翼的升力和铰链力矩产生影响．而式(17)表明升力面法中折叠翼总体气动力为各段机翼气动力的叠加,忽略了由于机翼厚度产生的低压区对其气动力的影响．因此,厚度项在分析Z形折叠翼的气动力时不可省略,将升力面法应用于Z形折叠翼的气动特性分析中较为局限,存在偏差．

4.2 CFD法与升力面法的比较

图10显示了Z形折叠翼在攻角为5°时,CFD法与升力面法计算机翼折叠过程中的气动力结果．两种气动模型的计算结果明显不同,特别是内外翼铰链力矩在折叠角较大时,偏差较大．

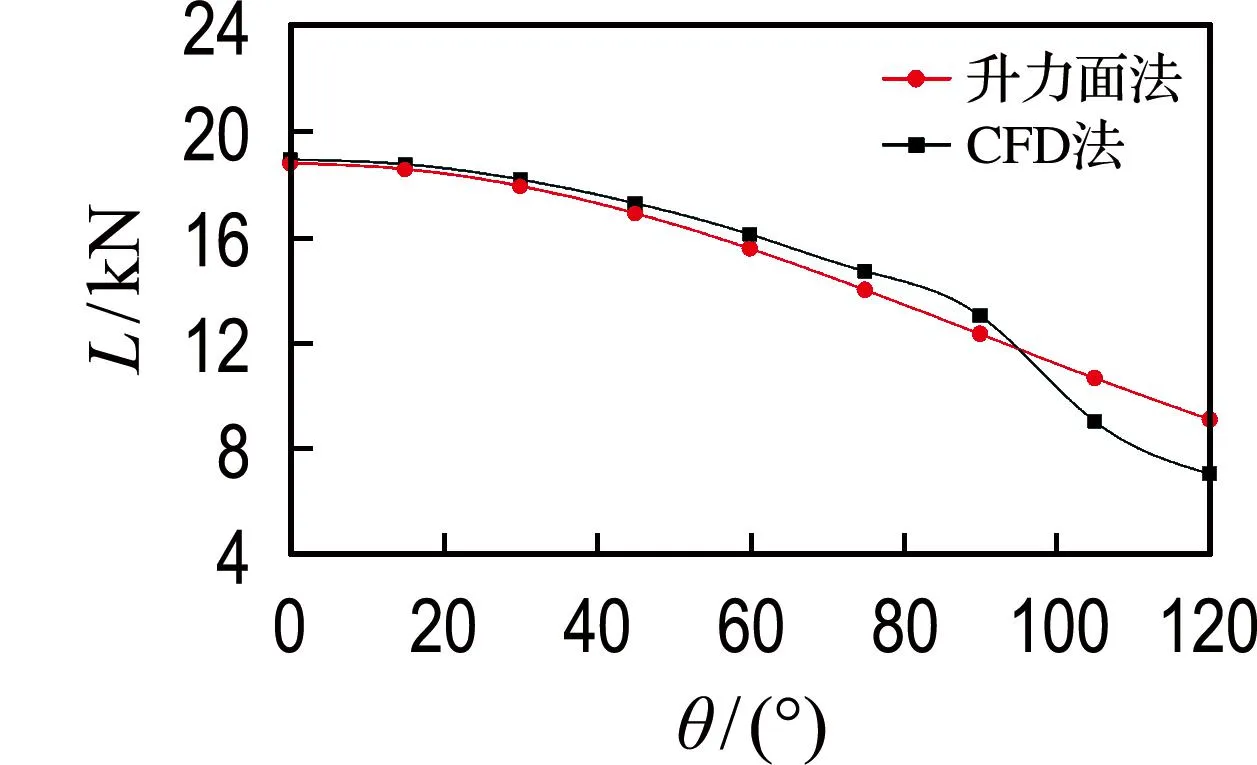
(a) 升力

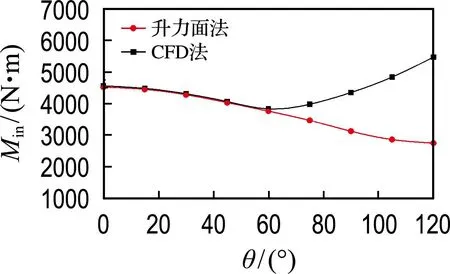
(b) 内翼铰链力矩

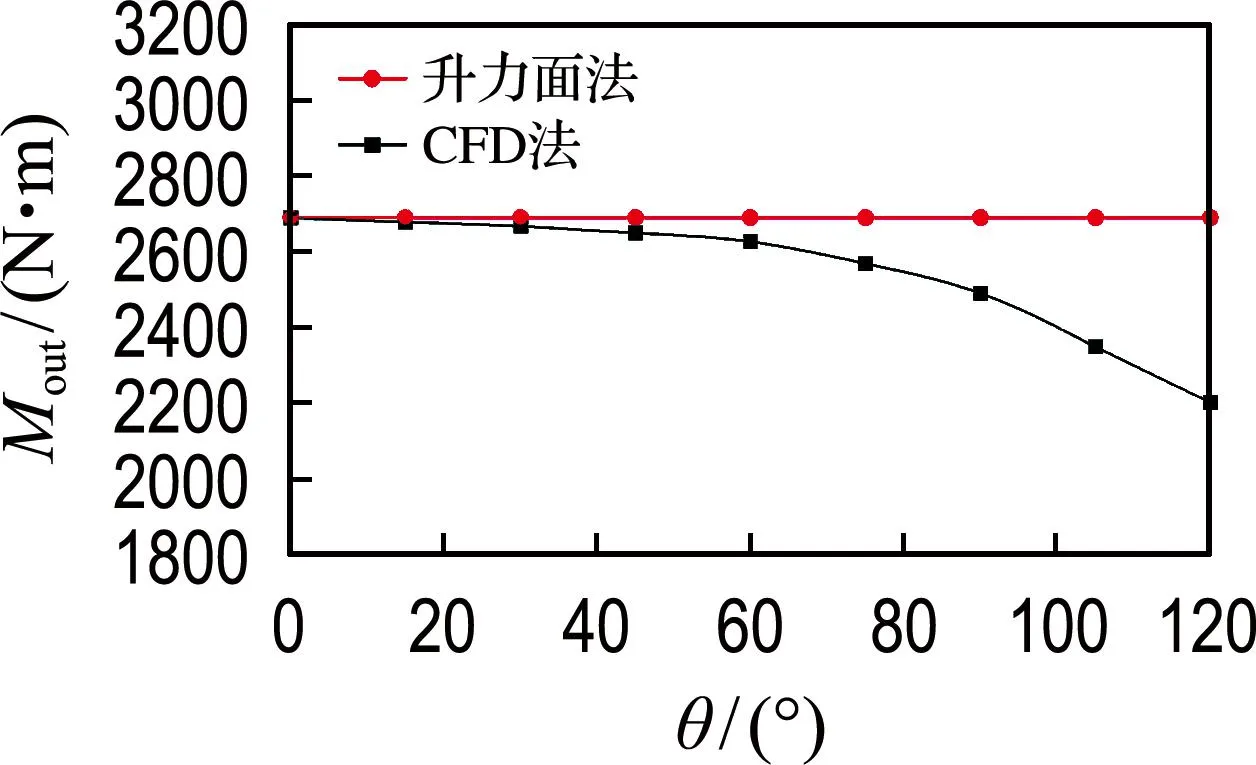
(c) 外翼铰链力矩

对比表明,差异首先表现在折叠翼升力的变化上,当折叠角较小时机翼厚度效应产生的内低压区强度大于外低压区,机翼整体升力相较于未考虑机翼厚度的升力面法计算结果偏大．但由于折叠角小,低压区强度小,因此二者偏差较小．当折叠角大于90°时,内外低压区强度大幅增加,低压区作用在机翼表面的气动荷载F1、F2方向向下,导致CFD法机翼升力小于升力面法计算结果．当机翼折叠到位(折叠角为120°)时,偏差最大,为29%．

其次,对于内外翼铰链力矩变化,机翼厚度效应导致的差异更为明显．CFD法模拟结果显示内翼铰链力矩随折叠角增加先减小后大幅增大,外翼铰链力矩持续减小．而升力面法计算结果显示,内翼铰链力矩减小,当折叠角大于90°后减小速度缓慢,外翼铰链力矩持续不变．对于内翼铰链力矩而言,由前文分析可知,影响内翼铰链力矩的因素有厚度效应产生的低压区变化和外翼折叠过程中的气动力臂变化两部分．而升力面法只考虑了外翼对于内翼铰链的气动力臂变化．当折叠角小于60°时,由于机翼厚度诱导流动产生的内外低压区强度较小,对内外翼升力影响较小,因此CFD法与升力面法计算结果相差不大．当折叠角大于60°后,机翼厚度效应明显增强,低压区对于铰链的影响远大于气动力臂变化的影响,导致内翼铰链力矩增大,两种方法计算结果偏差增大,最大偏差在折叠角为120°时,偏差为49%．对外翼铰链力矩,由于受折叠过程中厚度效应影响,外翼升力在持续增大的气动荷载F2的作用下减小,外翼铰链力矩减小,而升力面法并未考虑厚度项,因此外翼铰链力矩不变,二者偏差在折叠角为120°时达到最大,为22%．

上述分析表明,机翼厚度对于其气动荷载的分布和内外翼铰链力矩有很大影响,升力面法忽略厚度项,将导致升力和铰链力矩产生较大的模拟误差．在机翼折叠过程中,折叠角大于60°后,机翼厚度对折叠翼气动荷载及内外翼铰链力矩的影响逐渐增大,当折叠角为120°(全折叠状态)时,影响达到最大．

5 结 论

(1)Z形折叠翼在折叠过程中,机翼有效气动面积减小,升力、阻力系数总体呈下降趋势,表明折叠状态有利于折叠翼飞行器的高速冲刺．伴随着机翼折叠,全机的重心上移、气动焦点后移,机翼产生低头俯仰力矩,飞行器纵向稳定性降低,飞行高度下降,可偏转副翼增加攻角,实现配平．但其飞行控制系统模型和配平的攻角匹配问题仍有待研究．

(2)基于CFD法计算折叠翼气动特性发现,折叠翼在折叠过程中,机翼表面相互靠近,由于机翼存在厚度,产生气动干扰,形成低压区,当折叠角大于90°时,气动干扰尤为强烈．

(3)机翼厚度在机翼折叠过程中会对折叠翼的升力、内外翼铰链力矩等气动特性产生很大影响,导致折叠过程中升力在折叠角大于90°后大幅降低,内翼铰链力矩先减小后增大,外翼铰链力矩减小．

(4)基于升力面法和CFD法对折叠翼气动特性计算结果的对比表明,在计算Z形折叠翼升力和内外翼铰链力矩等气动特性时,机翼的厚度项不应忽略．采用忽略机翼厚度影响的升力面法计算折叠翼气动特性,会产生较大的模拟误差．