有限深度介质上梁非线性能量汇减振的Winkler地基实现

刘宗通, 马建军,2, 郭 颖

(1.河南科技大学 土木建筑学院,河南 洛阳 471023;2.河南省建筑安全与防护工程技术研究中心,河南 洛阳 471023)

结构物的振动问题普遍存在于土木工程、航空航天及机械工程的各个领域,振动抑制和控制一直受到工程师和科学家的普遍关注[1-4]。以土木工程领域为例,核电、大坝、桥梁等重要基础设施均会在地震作用下产生有害振动,并可能发生结构破坏。已有研究表明,结构物的抗震性能受其所处场地特征的直接影响,与土-结构相互作用(soil-structure interaction,SSI)效应密切相关。土-结构相互作用理论是结构物振动响应分析的基本理论之一,其效应多有利于提高结构物的抗震性能[5-10]。理论上讲,土-结构相互作用效应的减振机理是其导致结构物的振动能量传输到其所处场地中,并在场地中传播和耗散。

弹性地基梁模型是一类基本力学模型,被广泛应用于土-结构相互作用问题的静力和动力响应的理论分析[11-13]。已有研究表明,在土-结构相互作用系统的理论分析中,土场的力学特征可用多种地基模型展现,其中尤以Winkler地基模型的概念最简洁,在工程实践中的应用也最广泛。相应地,关于Winkler地基上梁的线性和非线性动力学特性的研究成果已十分丰富[14-15]。近年来,考虑土体质量的Winkler地基上梁的动力学研究日益受到重视,其在动力学建模时考虑了有限深度土体与其支承梁共同运动的效应,更精确地揭示了土-结构相互作用效应,也直观展现了土体质量对土-结构相互作用系统动力学特性的影响[16]。由于Winkler地基模型将土场离散为一系列彼此独立的弹簧,故在考虑土体质量的Winkler地基上梁的动力学建模过程中,可将有限长梁与弹性地基离散为由一系列彼此独立的弹簧连接的梁-小质量土体耦合系统。

非线性能量汇(nonlinear energy sink,NES)以其减振频带宽、鲁棒性好、轻质等优点逐渐受到各个工程领域的青睐[17-21]。非线性能量汇由附加质量,非线性刚度,阻尼元件组成,主体结构通过非线性弹簧和阻尼元件与NES较轻的附加质量连接,NES能有效吸收主体结构的动能,并将其耗散[22-24]。在非线性能量汇材料构成方面,Tian等[25]提出了基于超磁致伸缩材料的非线性能量汇振动能量俘获器。范舒铜等[26]将黏弹性材料应用于非线性能量汇,并讨论了其最佳参数取值范围。非线性能量汇在梁的振动控制中应用广泛,张登博等[27]研究了非齐次边界条件对轴向运动梁的动力响应的影响。Zhao等[28]建立了具有三次非线性的弹性连接器耦合的一般约束双梁结构动力学行为的通用模型。Zhang等[29]研究了边界上安装有惯性非线性能量汇梁的几何非线性对基础激励下系统响应和振动抑制效果的影响。从减振机理和构成形式等方面看,考虑土体质量的Winkler地基对其支承梁动力响应的影响与非线性能量汇的能量传递和耗散机制等具有相似性。理论上讲,土-结构相互作用对结构物动力响应的影响可能是一种具有非线性能量汇特征的作用效应,有限深度介质上梁非线性能量汇减振的Winkler地基实现具有可行性。

基于以上认知,本研究拟通过Winkler地基的参数设计,实现有限深度介质上梁的振动抑制。在研究过程中,利用考虑土体质量的Winkler地基模型,将有限深度弹性介质等效为附加质量并通过非线性弹簧和阻尼元件与Euler-Bernoulli梁连接,建立含非线性能量汇有限长梁的非线性动力学模型。利用Galerkin方法离散有限长梁的运动方程,采用增量谐波平衡法求得弹性介质-梁耦合系统的稳态响应。在利用龙格库塔法验证理论解正确性的前提下,分析了弹性介质质量、非线性刚度、阻尼等参数对其支承有限长梁动力响应和减振效果的影响,得到了弹性介质参数的最佳取值范围,实现有限深度介质上梁的非线性能量汇减振。

1 弹性介质上梁的运动方程

本文以弹性介质支承的简支边界有限长梁为研究对象,如图1所示。图1中：H为弹性介质有限深度,是一个微小量,能够使得NES与梁的质量比远小于1[30];L、b、h分别为有限长梁的长、宽和高;为简化分析,以未变形的梁端为坐标原点O,梁中轴线为x轴建立平面直角坐标系O-xy。

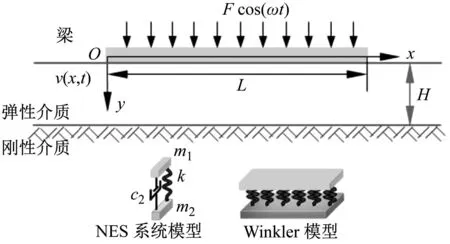
图1 弹性介质上有限长梁系统

由于弹性介质上梁类结构的轴向位移通常可忽略,本研究仅考虑梁的横向位移。将有限长梁与弹性地基离散为由一系列彼此独立的弹簧连接的梁-小质量土体耦合系统,并取梁下有限深度弹性介质作为NES的较轻附加质量,基于Winkler地基模型和Euler-Bernoulli梁理论,依据带有附加非线性能量汇线性梁系统的运动方程[31],可得弹性介质-梁耦合系统的非线性运动方程

k(v-u)3=Fcos(ωt)

(1a)

(1b)

为便于分析,引入无量纲参数

(2)

将式(2)代入式(1),可得无量纲运动方程

k(v-u)3=Fcos(ωt)

(3a)

(3b)

其中,为便于表述,已忽略无量纲参数的上标。

2 Galerkin离散

依据梁的简支边界条件,利用Galerkin方法[32],设：

(4a)

(4b)

将式(4)代入式(3),可得：

Fcos(ωt)

(5)

(6)

将式(5)和(6)同时乘以sin(jπx),并在x=0到x=1范围内积分,可得：

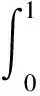
(7)

(8)

令式(7)等号左边为0,即可实现对控制方程的N阶Galerkin截断,将式(7)、(8)转化为含有2N个未知数Vj、Ui(i、j=1,2,…,N)的常微分方程组[33]。可得：

取N=1,式(9)、(10)可用矩阵向量形式表示为

(11)

其中

对于系统的强制响应,可以在等式的右侧添加激励项。式(11)变为

(12)

3 增量谐波平衡法求解

引入新的时间尺度

τ=ωt

(13)

则式(12)可写为

(14)

应用增量过程,定义系统在激励大小为F0,激励频率为ω0时的振动状态为xi0,i=1,2,则其临近状态可以用增量形式表示为

xi=xi0+Δxi,i=1,2

f=f0+Δf,ω=ω0+Δω

(15)

式中,Δxi,Δf,Δω为微小增量。将式(15)代入式(14),可将高阶小量忽略,得：

(16)

经过一系列推导,可得迭代方程(17),推导过程以及式(17)中矩阵详见附录A

(17)

求解时,先给出一组稳态周期振动的猜测解A,进而根据式(17)求得余量R,若R小于设定的容许值,则给ω一个增量,即Δω

ωi+1=ωi+Δω

(18)

而后进入下一个迭代过程,若R大于容许值,则执行以下迭代过程

(19)

直到余量R达到容许值内。

4 数值计算

为进行数值计算,根据参考文献[34],表1给出了所需的物理参数。

表1 梁的物理参数

4.1 特征方程求解

忽略式(3)中的非线性项、阻尼项、外激励项,可得梁的线性无阻尼运动方程

(20)

式(20)解的形式可设为v(x,t)=φ(x)eiΩt,Ω为梁的固有频率;i为虚数符号;将其代入式(20),可得解的形式为

φ(x)=C1cosαx+C2sinαx+

C3coshβx+C4sinhβx

(21)

简支梁的边界条件为

φ(0)=0,φ″(0)=0

φ(1)=0,φ″(1)=0

(22)

可得求解梁固有频率的超越方程

(α4+β4+2α2β2)sinαsinhβ=0

(23)

利用式(23),可求得梁的第i阶固有频率Ωi,如表2所示。忽略式(12)中的NES,采用IHB方法进行数值计算,得出幅频曲线和固有频率,由表2可知,两种方法得到的前四阶固有频率一致。

4.2 数值验证

利用四阶龙格库塔法验证本文理论解的正确性。为进行数值分析,系统参数取：

c1=0.08,c2=1,k=1×106,ε=0.3,f=0.04

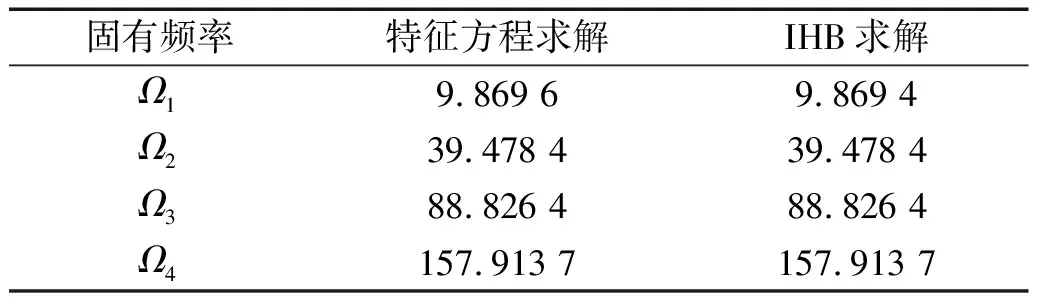
表2 简支梁固有频率

在增量谐波平衡法求解过程中,取n=2,则x1,x2可表示为

x1=a11cosτ+a12cos 3τ+b11sinτ+b12sin 3τ

(24a)

x2=a21cosτ+a22cos 3τ+b21sinτ+b22sin 3τ

(24b)

取初始条件为

a11=a12=b11=b12=0.001

a21=a22=b21=b22=0.000 1

(25)

IHB方法的结果显示A11≫A12,故仅考虑A11。图2给出了分别采用IHB和RKM方法求得的梁幅频响应曲线。由图2可知,两种方法得到的结果一致,验证了理论解的正确性。

图2 IHB和RKM数值结果对比

5 NES的有效性

图3给出了弹性介质上梁的共振响应时程曲线。在图3(a)中,系统参数为c1=0.08,c2=1,k=1,ε=0.3,f=0.04,ω=9.869 6,比较了考虑NES和不考虑NES梁的位移响应,虚线和实线分别表示无NES和有NES的情况下梁的响应。结果表明,在外部激励频率等于梁的一阶固有频率时,横向振幅非常大。相比之下,若考虑NES,则梁的振动幅值显著减小。在图3(b)中,检验了NES在外部激励频率等于梁的二阶固有频率时的鲁棒性。图3(b)中梁系统的参数为c1=0.08,c2=1,k=1,ε=0.3,f=0.04,ω=39.478 4,图3(b)给出了不考虑NES梁响应到稳态的漫长衰减过程。相比之下,NES可以迅速将振幅降低到较低的稳态响应,表明NES能够快速有效地吸收共振条件下的振动能量,并且具有较好的鲁棒性。

(a) 一阶共振响应

(b) 二阶共振响应

6 参数优化

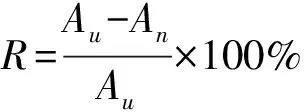
6.1 质量比分析

图4给出了质量比ε变化时的幅频响应曲线,考虑NES梁系统的其他参数为c1=0.08,c2=1,k=1×103,f=0.04。为便于分析,计算过程中通过改变弹性介质质量实现参数ε的变化。图4中实线表示不考虑NES条件下梁的幅频响应,其余线型表示考虑NES梁的响应。由图4可知,随着质量比ε的增大,梁的响应幅值不断减小,同时梁的幅频曲线共振峰越来越平缓,因此弹性介质作为NES具有较宽的减振频带,体现了非线性能量汇的宽频带的特点。表3给出了不同质量比ε条件下梁的响应峰值对应的频率和最大共振振幅衰减率。由表3中峰值对应的频率随参数ε的变化情况可知,随着质量比ε的增大,考虑NES梁系统的固有频率增大并越来越接近不考虑NES梁系统的固有频率。当质量比ε增大到一定程度时,对固有频率的影响显著降低。随着质量比ε的增大,衰减率不断增大,减振效果越显著,但当质量比ε增大到一定程度时,衰减率几乎没有变化。表明在分析弹性介质上梁的动力响应时仅需考虑有限深度内弹性介质的影响即可。

图4 不同质量比ε条件下梁的幅频响应

表3 不同ε下系统的固有频率和衰减率

表4 参数ε对应的弹性介质密度

由表4可知,在弹性介质的密度为2.198 5×103kg/m3时,梁系统响应的衰减率几乎达到最大值。弹性介质质量继续增加对系统响应的衰减率几乎没有影响,因此弹性介质的密度存在最佳范围。工程经验表明,黏性土的密度通常为1.8～2.0×103kg/m3,砂土的密度通常为1.6～2.0×103kg/m3,并未达到弹性介质的密度最佳范围。因此,需要采用地基处理改善弹性介质的物理力学性质,使其密度达到最佳范围。例如,对有限深度地层进行处理,采用粉煤灰(密度为1.9～2.9×103kg/m3)改性换填,改善地层的物理力学性质,则能满足密度要求。显然,可通过地基处理改善弹性介质的物理力学性质,达到预期的振动抑制效果。

6.2 阻尼分析

图5给出了阻尼系数c2变化时的幅频响应曲线,考虑NES梁系统的其他参数为c1=0.08,k=1×103,ε=0.2,f=0.04,研究了NES阻尼对减振效果的影响。由表5和图5可知,阻尼越大,幅频响应曲线峰值先减小后增大。表明随着阻尼的增大,NES的减振效果先增强后减弱。显然,NES的阻尼有一个最优值,本研究中阻尼的最优参数为c2=2。然而,固有频率则随着阻尼的增大而减小,且当阻尼增大到一定程度时,对固有频率的影响显著减弱。

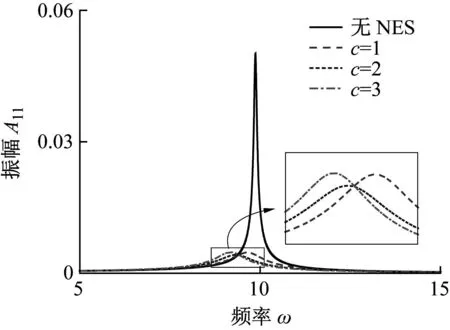
图5 不同阻尼系数c2条件下梁的幅频响应

表5 不同c2下系统固有频率和衰减率

6.3 非线性刚度分析

图6显示了非线性刚度k变化时的幅频响应曲线,考虑NES梁系统的其他参数为c1=0.08,c2=1,ε=0.2,f=0.04,分析了NES非线性刚度对减振效果的影响。由表6和图6可知,非线性刚度越大,幅频响应曲线峰值越小;非线性刚度在1～10 000区间内时,对固有频率的影响较小,并且对减振效果也影响较小,且此时已具有较好的减振效果。当非线性刚度增大到104后,对梁的减振效果影响较大。随着非线性刚度的增大,固有频率逐渐增大,逐渐接近不考虑NES梁的固有频率,同时梁的衰减率不断增大,减振效果越来越好。当非线性刚度增大到106时,减振频带带宽显著增大,当增大到107时,幅频曲线共振区出现振幅跳跃现象,共振峰发生明显变形,动力学特性变的更加复杂,一定频率范围内的周期解不稳定。因此,可将106作为最佳的非线性刚度。

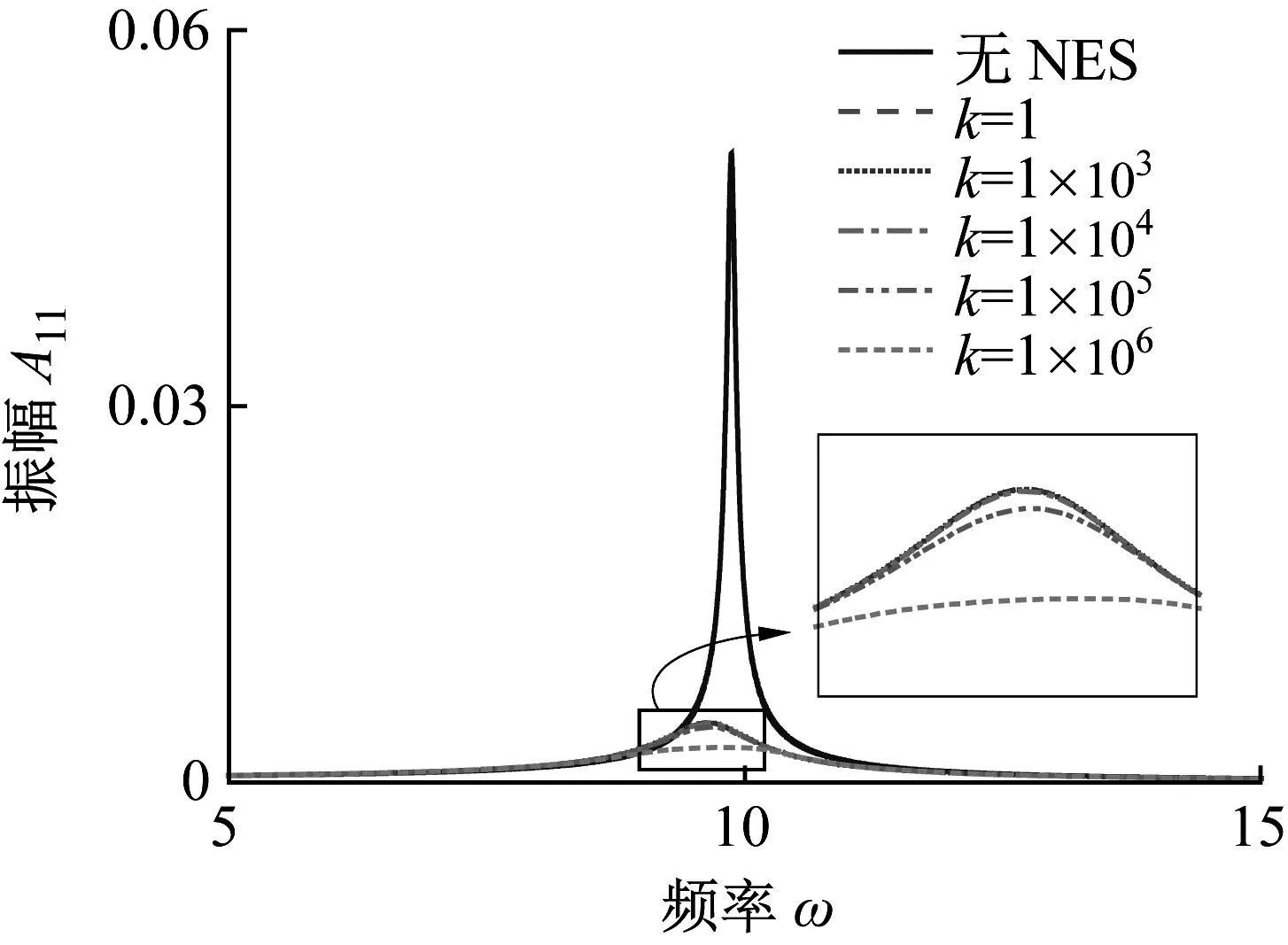
图6 不同非线性刚度k下梁的幅频响应

表6 不同参数k下系统固有频率和衰减率

6.4 最佳优化结果

利用图4、图5、图6和表3、表5、表6的结果,分析NES的参数ε、c2和k的影响并寻求最佳的参数取值范围,结果表明当c2=2,k=1×106,ε=0.3时,最大振幅达到最小值,此时最大振幅为0.002 614,衰减百分比为94.84%。对最佳参数的无量纲值进行有量纲值转换,可得c2为6.809 kN·s/m2,k为6.976×108N/m3,同时根据参考文献[35],土体阻尼系数在0～420 kN·s/m2,刚度系数在1 000～4 600 kN/m2可知,最佳参数中的c2在合理范围内,而非线性刚度由于单位是N/m3无法进行准确比较。图7给出了最优参数下梁动力响应的幅频曲线和相平面图,其中幅频曲线如图7(a)所示,图7(b)为外激励频率为9.87时的最优参数的相平面图。如图7(b)所示,最优参数条件下梁动力响应的相平面图为一闭合曲线,表明梁系统做周期运动,是稳定的。

7 结 论

利用非线性能量汇理论,本文建立了考虑有限深度弹性介质运动影响的弹性介质-梁耦合系统的非线性动力学模型。运用增量谐波平衡法进行了有限长梁在简谐激励下的非线性振动分析,求得了考虑NES和不考虑NES梁的稳态响应,分析了弹性介质质量、非线性刚度、阻尼对梁系统的动力响应的影响,实现了利用Winkler地基设计达到结构振动抑制的目的。得到如

(a) 幅频曲线

(b) 相平面图

下主要结论：

(1) 将有限深度弹性介质等效为NES附加质量,能有效抑制系统的振动,且具有良好的鲁棒性,能够在较宽的频带内大幅降低系统的响应幅值。

(2) 仅有限深度弹性介质对系统的动力响应有显著影响,通过技术手段进行弹性地基设计,改善弹性介质的物理性质可实现预期的振动抑制效果。

(3) 随着NES阻尼的增大,系统的固有频率减小,并存在最优阻尼;随着非线性刚度的增大,系统的固有频率增大并不断逼近不考虑NES的固有频率。

(4) 当弹性介质的参数为ε=0.3,c2=2,k=1×106时,能有效抑制其支承梁的振动响应,共振振幅降低约95%。

利用非线性能量汇理论,可通过共振幅值的降低精确阐释土-结构相互作用对弹性介质上梁受迫振动的抑制效应。在后续研究中,应关注响应在弹性介质中的传递、衰减和耗散的演变规律,量化评估有限深度弹性介质耗散的能量,为土-结构相互作用系统的能量单向传递设计和应用提供理论基础。

附录A

(A.1)

其中

式(A.1)内含有立方刚度,其稳态周期解可假设为

(A.2)

其中

D=[cosτ,cos 3τ,…,cos(2n-1)τ,

sinτ,sin 3τ,…,sin(2n-1)τ]

Ai=[ai1,ai2,…,ain,bi1,bi2,…,bin]T

ΔAi=[Δai1,Δai2,…,Δain,Δbi1,Δbi2,…,Δbin]T

系统的稳态周期解可以表示为

x0=SA,Δx=SΔA

(A.3)

其中

将式(A.3)代入式(A.1),并应用伽辽金平均过程,有

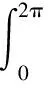
(A.4)

式(A.4)经推导可表示为

KmcΔA=R+RmcΔω+RfΔF

(A.5)

其中

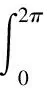
式(A.5)中未知增量的个数比线性方程的个数多两个,首先必须令其中一个增量为0,在本文中研究激励大小固定情况下的幅频响应,所以可设ΔF=0,即激励幅值恒定,式(A.5)可写为

KmcΔA=R+RmcΔω

(A.6)

我们需要关注的是振动幅值随激励频率ω的变化情况,因此令Δω为主动增量。在每一个解算点处,主动增量Δω=0,利用方程(A.6)可对ΔA进行迭代求解,即有

(A.7)