基于时间有限元的非线性系统周期响应求解及稳定性分析

郑永进, 汪 利, 刘祚秋

(中山大学 航空航天学院,深圳 518107)

非线性现象广泛存在于实际结构的动力分析之中,主要有几何非线性、材料非线性与接触非线性三种来源[1]。在早期的非线性研究中,一般通过线性逼近的方式将非线性问题转化为线性问题进行求解,对于简单问题所得近似解能够满足工程界的精度要求,但是随着工程问题的复杂程度增大、分析时间增加,系统内部的非线性因素会使得分析和计算中出现非线性系统特有的现象,如多值响应、极限环、弛缓、分岔以及混沌等[2]。比如,多值响应现象主要出现在受强迫振动的非线性系统中,强非线性系统在谐波激励下可能有多个解,利用改变激励频率或幅值的方式,可以发现系统振幅出现了跳跃现象,也意味着多解的存在[3];Bunonmo[4]在求解Van der Pol系统时,对极限环以及弛缓现象进行了分析研究,在不同的非线性系数下系统所产生的振动现象也不相同;Bernardo等[5]详细描述了由分岔引起的复杂动力学行为;Venkatesan等[6]对Duffing-van der Pol系统中的分叉与混沌现象进行了分析。

为了解析这些特有的非线性现象,通常需要求得非线性系统的稳态响应(包括周期解),进而分析解的分岔和稳定特性。根据频域或时域上的分析特点,主要出现了两类非线性系统稳态响应求解方法,即频域的谐波平衡法[7]和时域的打靶法[8]。谐波平衡法主要根据稳态响应的频域特性,使用Fourier级数近似表示周期解或准周期解。该方法能够直接获取解的频响特征,且对于光滑或弱非线性系统,使用少量的级数项就可得到高精度的解,具有极高的计算效率[9];但是,在求解非光滑以及强非线性问题时,谐波平衡法需要选用大量的谐波项,非线性项的谐波系数计算也十分困难,导致计算效率急剧降低。打靶法则是在通用数值积分方法上,引入周期边界条件求得稳态响应的初值。打靶法能够适用于各种问题,包括接触、冲击和摩擦等非光滑问题[10],且能够直接得到系统的传递矩阵,进而判定周期解的稳定性;但是在面对大规模弱非线性及光滑问题时,计算过程相对来说十分繁琐、代价较为高昂,且无法直接得到频域特性。

与以上两类方法不同,本文旨在提出一种基于时间有限元的非线性系统周期响应求解新方法。时间有限元是一种基于伽辽金变分公式和分段多项式插值的方法,与一般的基于有限差分的数值积分方法相比,时间有限元求解精度高,计算量适中[11],并且在面对激励快速变化问题时,方法尤为精确[12]。在研究过程中,许多学者基于不同的变分公式、不同问题提出了相应的时间有限元方法[13-15]。Hulbert建立了结构动力学方程的时间不连续伽辽金有限元法,并证明了算法的稳定性和收敛性[16];Wang等[17]建立了一种Petrov-伽辽金型的时间有限元法,证明了在相同的时间步长下,针对线性问题时间有限元法可以提供比Newmark-β法更精确的响应解,周宇等[18]研究表明算法的周期延长率几乎为0,意味着时间有限元的计算结果不会发生周期漂移,对实际工程的应用十分重要;Qin等[19]提出了一种新型的时间求积单元,显著提高了计算效率。以上的各类时间有限元法主要面向线性动力系统的瞬态响应分析,本文则是提出一种新型的时间有限元,以求解非线性系统的稳态响应,显著拓展了时间有限元的应用范畴。该方法在稳态响应伽辽金变分公式基础上,代入位移响应的三次样条插值,并结合牛顿迭代法进行求解。由于时间有限元具有精度高、能处理快速变化的激励等特点,所提方法能高效、高精度地求解非光滑周期荷载下的稳态响应。此外,考虑到时间有限元也能求解瞬态响应,可从系统矩阵中得到周期系统的传递矩阵,进而直接根据传递矩阵的特征值判断解的稳定性。

1 非线性系统周期响应的时间有限元方法

1.1 基本原理

考虑周期荷载作用下的结构非线性动力系统,其控制方程的一般形式为

(1)

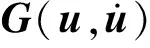
(2)

为便于后续分析,令外荷载f∈L2(IT)在时间区间IT=[0,T]上平方可积,此时系统的速度和位移也是连续的,考虑周期边界条件,系统位移u从属于如下空间

(3)

式中,H2(IT)为二阶导数平方可积函数的空间。

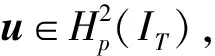
(4)

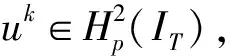
(5)

(6)

(7)

求解线性问题(6)即可从已有位移解uk(t)得到迭代更新解uk+1(t),反复迭代直至满足收敛条件,最终得到满意的结果。

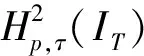
(8)

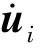
(9)

将插值函数代入线性方程,可建立单元刚度矩阵Di和单元荷载向量Fi

(10)

通过单元组装,可得到整体刚度矩阵D和荷载向量F。为了便于后续分析,对刚度矩阵和荷载向量作分块处理,即

(11)

(12)

其中：

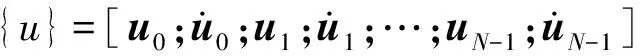
(13)

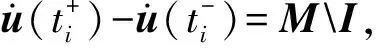
综上所述,时间有限元的求解过程为：

步骤1给定初值{u}0,设置收敛精度ε=10-6,以及迭代步数k=1;

步骤2基于上一步的解{u}k-1计算整体刚度矩阵D和荷载向量F,引入周期边界条件得到如式(12)的刚度方程。解刚度方程得到迭代更新解{u}k;

步骤3若不满足收敛条件,即

(14)

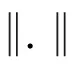
步骤4若满足收敛条件,则终止迭代,得到问题的周期解。

1.2 周期解的稳定性

(15)

令传递矩阵A的特征值中具有最大模的特征值为λ,该特征值也称Floquet乘子,可直接用于判定系统的稳定性：|λ|<1,周期解是稳定的;|λ|>1,周期解是不稳定的;|λ|=1则通常处于临界分岔状态,根据特征值λ实部与虚部的取值,可能出现倍周期分岔、Hopf分岔、鞍结分岔等。

从上可知,周期解稳定性分析的关键在于得到传递矩阵A。为了获取传递矩阵A,需要计算初值扰动下的系统响应,求解下述线性扰动方程

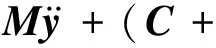
(16)

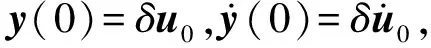
(17)

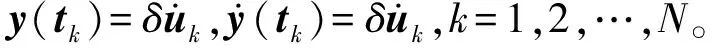
(18)

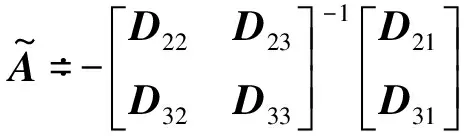
2 数值算例

本章主要以Duffing系统的受迫振动为例,验证所提时间有限元在非线性系统周期响应求解和稳定性分析上的有效性和正确性,尤其要突出所提方法在非光滑周期荷载作用下的可行性。

2.1 受余弦荷载作用的单自由度系统

考虑一个含阻尼的单自由度Duffing系统,对其施加简谐外激励,其控制方程如下

f(t)=0.2cos(0.8t)

(19)

式中：m=1 kg;c=0.05 N·s/m;k=1 N/m;α=0.1 N/m3;T=2.5πs。

为了进行时间有限元分析,将时间区间[0,T]划分为N=24个均匀分布的单元。同时,为了验证解的正确性,以打靶法的解作为参考。图1给出了时间有限元所求的周期响应,图2给出了响应的相图,两图的结果均与打靶法的结果进行对比。可以看出,时间有限元的结果与打靶法的结果几乎重合,验证了时间有限元在非线性系统周期响应求解中的正确性。此外,还可根据时间有限元计算得到系统的Floquet乘子|λ|=0.140 1,同时,为了对比,还可以计算打靶法的Floquet乘子|λ|=0.140 3。可以看出,时间有限元给出了正确的Floquet乘子计算结果,该结果表明周期解是稳定的。为了进一步探讨非线性系数α对系统稳定性的影响,通过弧长法可得到基频振幅与参数α的关系,如图3所示,其中实线表示稳定解,虚线表示不稳定解。选取α=-0.1,此时系统存在3个周期解,其中2个为稳定解,1个不稳定。着重考虑不稳定解,此时时间有限元和打靶法的计算结果如表1所示。以打靶法为参考,时间有限元显然给出了正确的不稳定周期解及稳定性判断结果。时间有限元显然可以得到不稳定周期解,并准确判断出其稳定性。

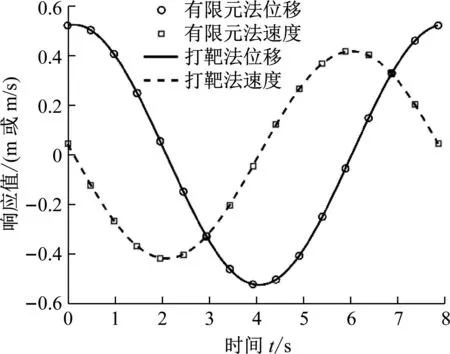
图1 单自由度非线性系统位移和速度响应

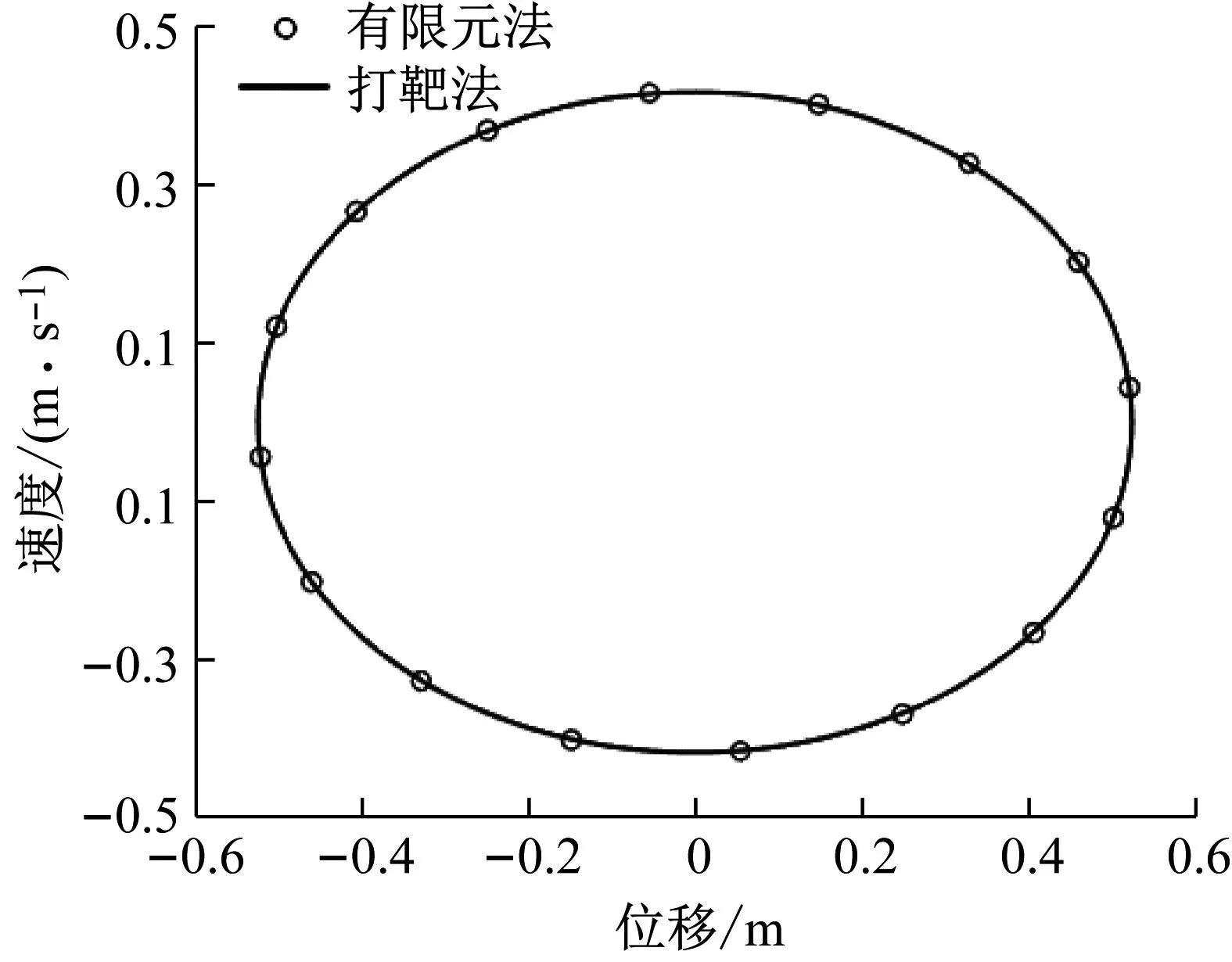
图2 单自由度非线性系统相图

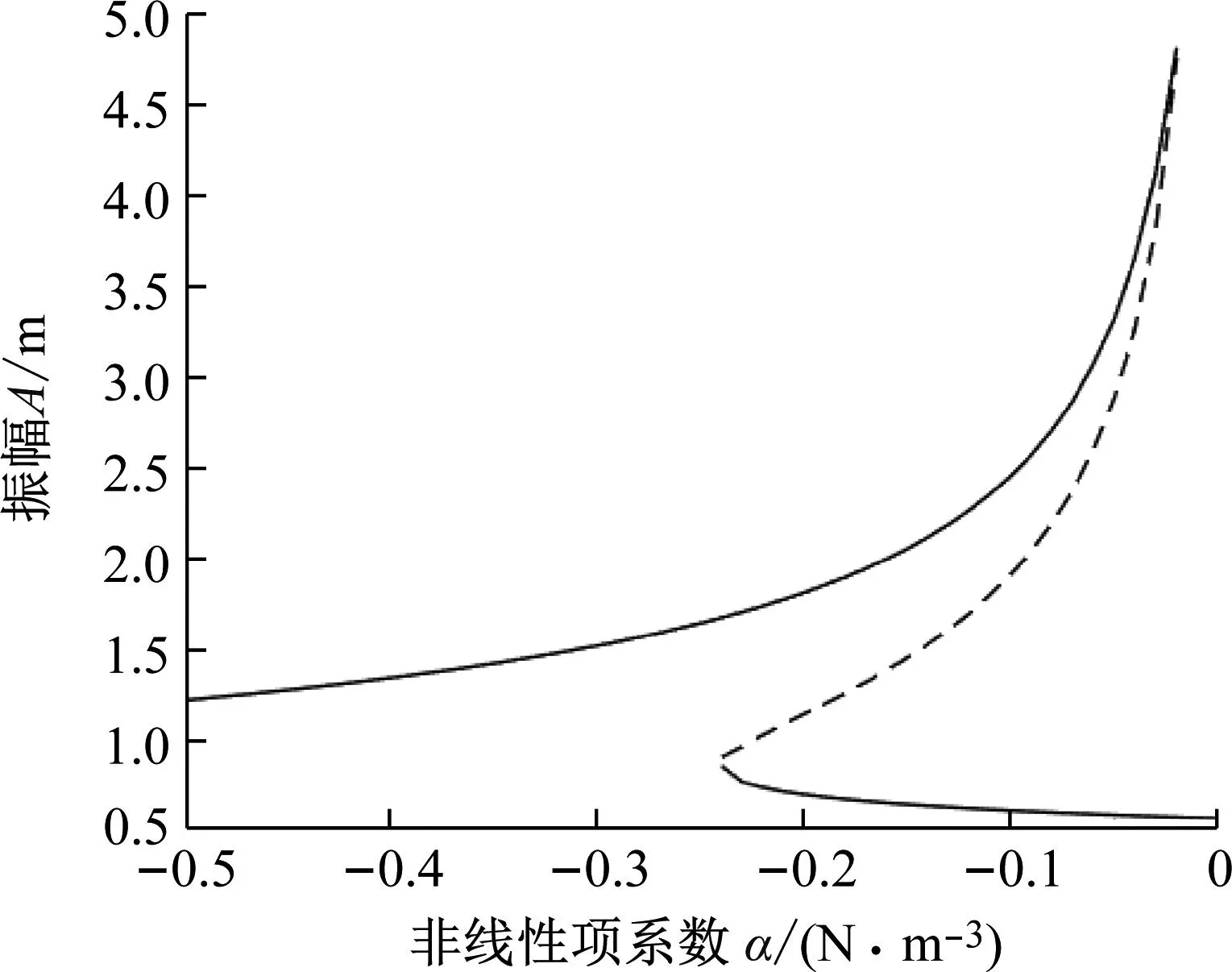
图3 基频振幅-非线性项系数关系图

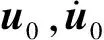
(20)

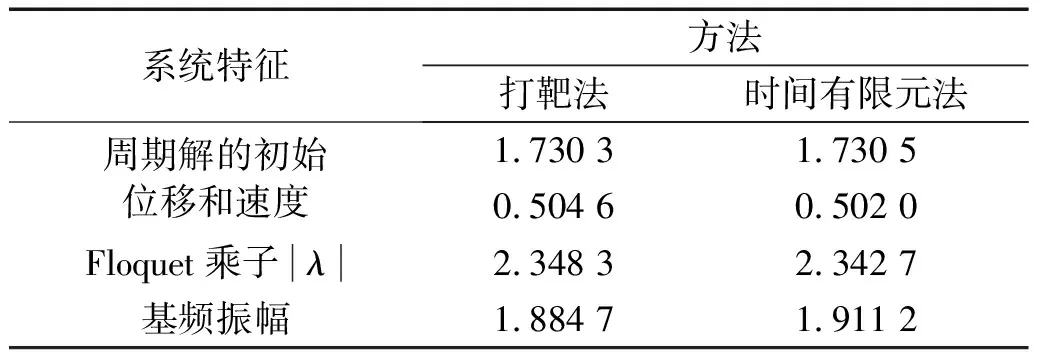
表1 打靶法与时间有限元法计算结果对比

图4给出了初始状态误差随单元尺寸τ的变化趋势。可以看出,随着网格加密,时间有限元的初始状态误差越来越小,且该误差达到了2阶收敛速度,即error∝τ2。混合荷载示意图如图5所示。

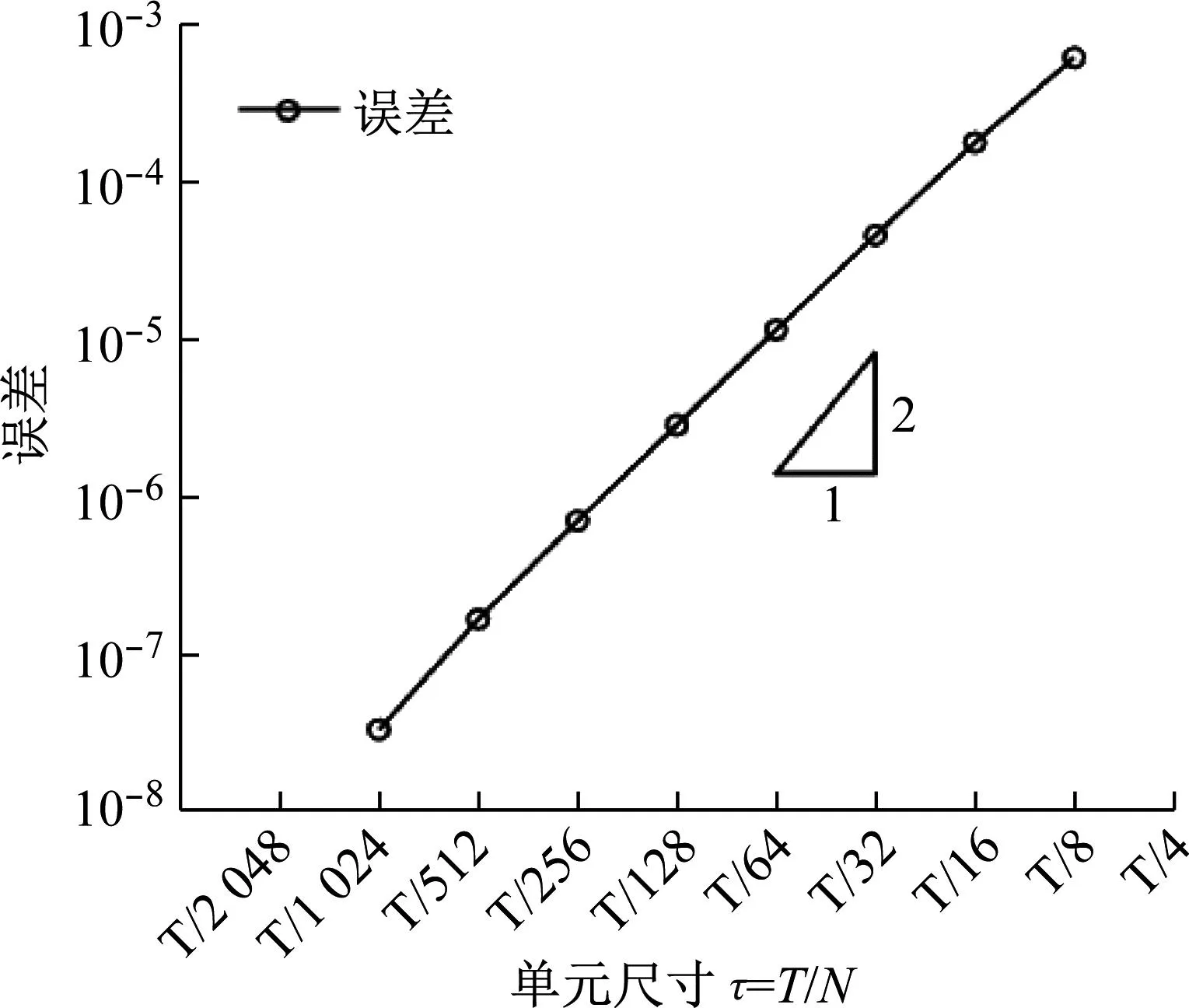
图4 初始状态误差随单元尺寸τ的变化趋势

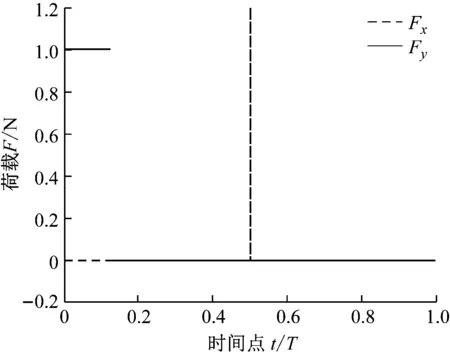
图5 混合荷载示意图

2.2 受阶跃和冲击周期荷载作用的多自由度系统

考虑如下两自由度Duffing方程

(21)

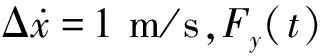
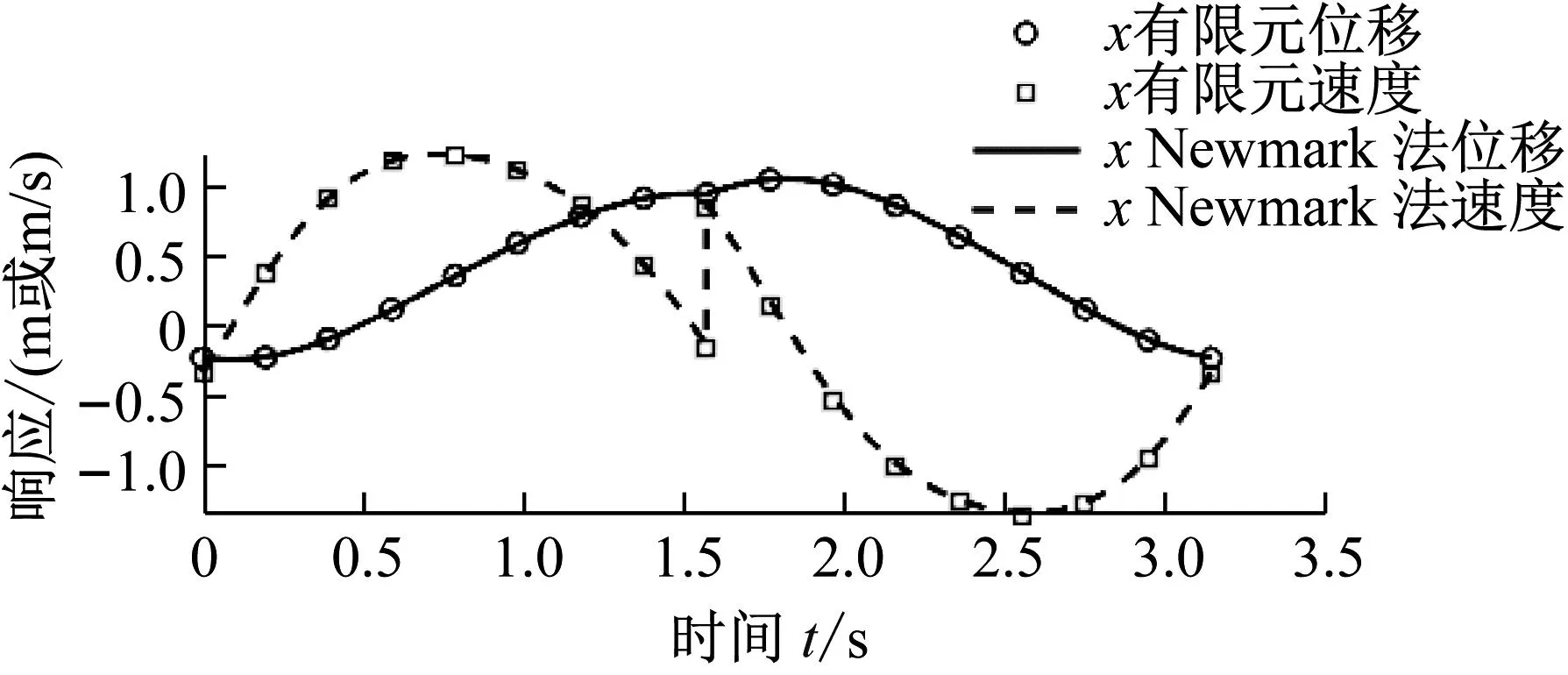
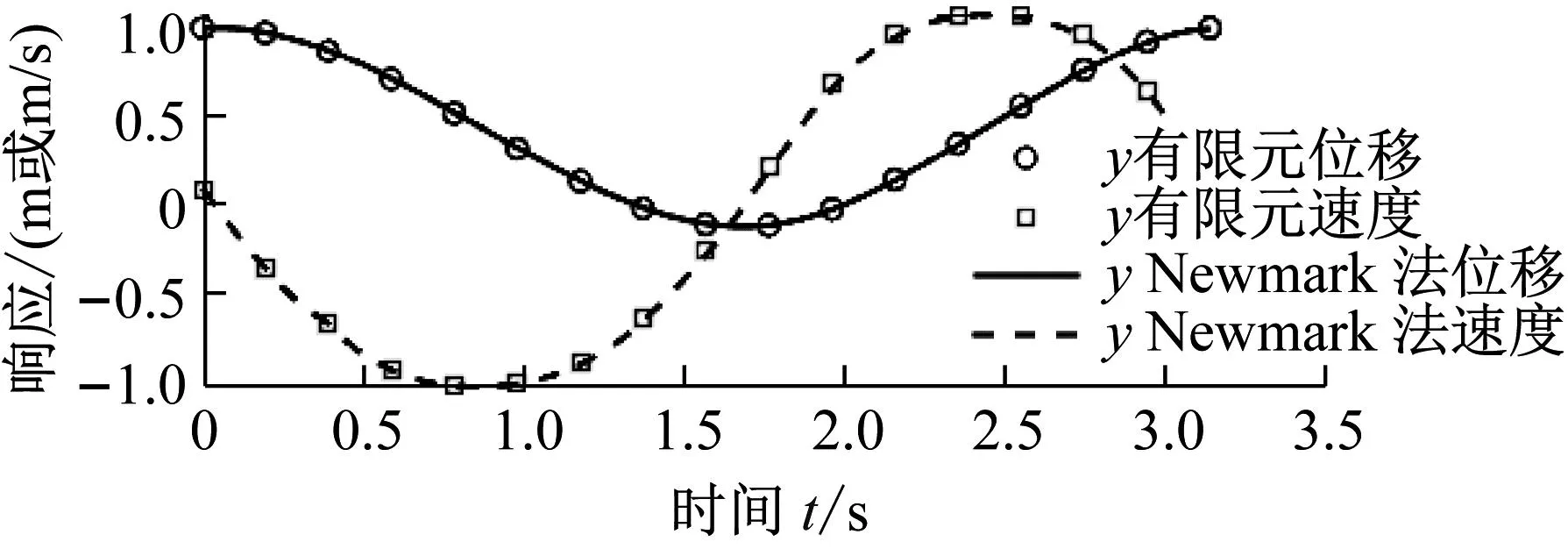
图6 时间有限元法和Newmark法求多自由度非线性系统位移和速度响应的对比图

使用时间有限元,给定单元数目N=24,可以得到两个自由度x,y的位移速度响应,如图6所示。同时,以时间有限元所得到的初始状态作为初值,使用参数为(γ,β)=(1/2,1/6)的Newmark-β法计算系统的振动响应,经过50个周期后,解达到稳定,取此稳定后的周期解作为参考解。对比时间有限元与参考解(见图6),可以看出,时间有限元给出了准确的周期响应计算结果,能够很好地处理冲击荷载引起的速度突变。同时,通过计算,还可得到Floquet乘子|λ|=0.986 0<1,而参考解是从瞬态响应经过长时间稳定得来,它是稳定的,有限元的解与参考解吻合,也表明了稳定性判断的正确性。

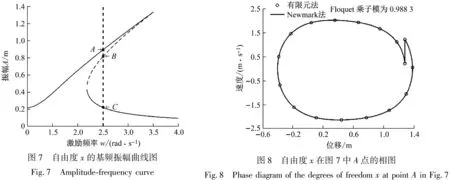
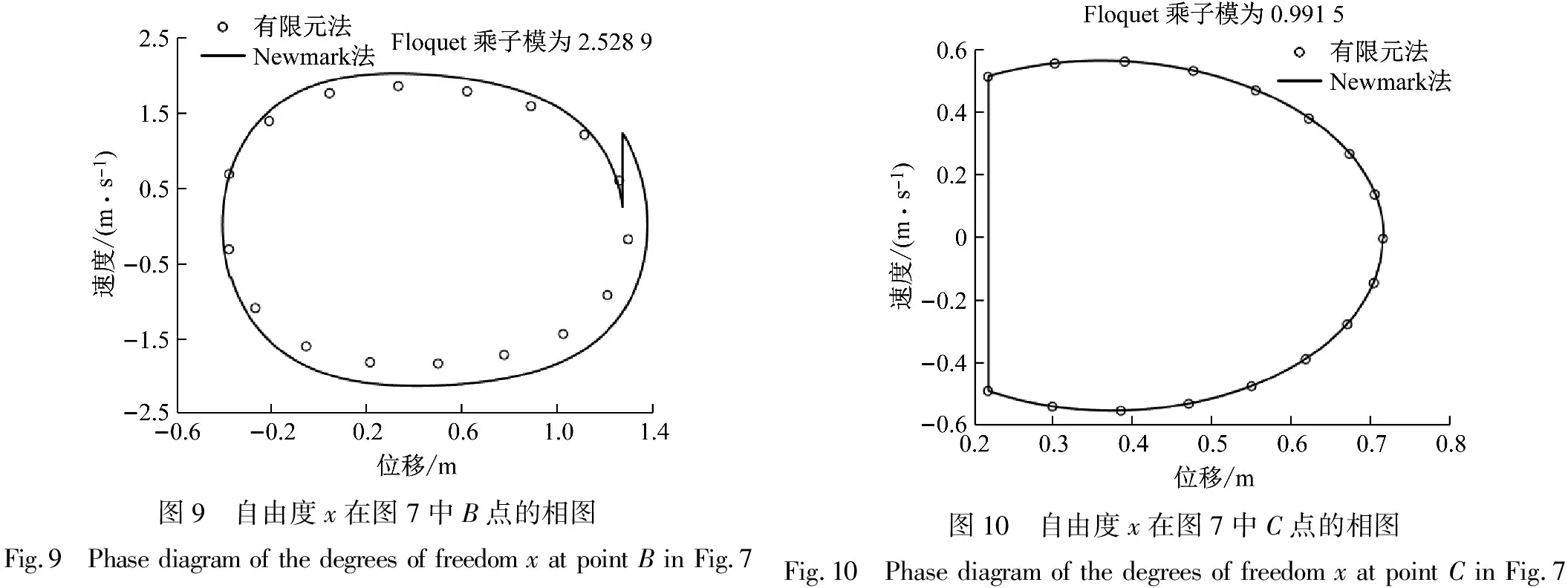
为了进一步探讨外激励频率ω对系统稳定性的影响,通过弧长法可得到基频振幅与外激励周期频率ω的关系,最终可得x自由度基频幅值曲线,如图7所示,其中实线表示稳定解,虚线表示不稳定解。取ω=2.5 rad/s,此时系统存在3个解,分别如图7中所标A,B,C三点。A,B,C三点对应的x坐标相位曲线及相应的Floquet乘子如图8～10所示。可以看出,A点,C点对应的两个稳定解与参考解完美相符,而B点对应的不稳定解则明显偏离参考解,这正好验证了周期响应求解和稳定性判断的正确性。

3 结 论

本文在伽辽金变分公式的基础上,提出了一种非线性系统周期响应求解的时间有限元法,并基于时间有限元的系统矩阵,直接求出了系统的传递矩阵,进而快速判断解的稳定性。结合弧长法,还可得到非线性系统的频响曲线。数值算例表明,所提方法精度高,能有效处理非光滑周期激励(如阶跃或冲击周期荷载),

能给出正确的稳定性判断结果,为非光滑问题的周期响应分析提供了一种新的思路。