舱段主动隔振系统作动器配置优化

巫 頔, 谢溪凌, 张志谊,

(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.上海交通大学 振动、冲击、噪声研究所,上海 200240)

舱段隔振系统主要用于减少振源设备(主机、辅机等)的振动向弹性壳体传递。主动隔振具有更宽的振动抑制频带,国内外学者对主动隔振展开了大量的理论研究与实践,Daley等[1]设计了电磁作动器与弹簧并联的主动隔振器用于浮筏隔振,使线谱振动衰减25 dB。Yang等[2]进行了大型主动隔振系统振动控制实验,采用前馈控制算法取得了最高36 dB的振动抑制性能。Ma等[3]针对双层隔振-壳体模型,分析了不同激励形式下作动器安装位置、数目对控制效果的影响。目前已有的主动隔振平台多采用单向作动器,振动传递控制不完备,仅能部分抑制功率流向基础传递[4],而多向主被动控制带来更好的控制效果的同时,引入了更多控制通道,导致控制系统更为复杂。主动隔振系统的控制效果不仅取决于控制律设计,还取决于的作动器、传感器的位置选取。通常的控制是开启所有作动器,随之而来的问题就是控制通道多,在某些激励下可能存在冗余。较好的控制方式是根据激励源特征,通过优化明确主导路径并实施控制,在保证控制效果的前提下,降低控制复杂度。

近年来,研究者对振动主动控制的通道配置优化,即作动器、传感器位置及数量的优化准则和优化方法,开展了一些研究。Hamdan等[5]提出了基于模态空间能控度/能观度概念,Bruant等[6]在能控度/能观度Gramian优化准则中考虑了模型溢出效应。Ramesh等[7]与Güney等[8]分别采用线性二次型指标和闭环H2范数指标优化简支梁上传感器、作动器的布置。Wang等[9]针对索网结构中压电作动器的布置问题,设计H2控制器,并采用从扰动到响应的闭环传递矩阵的H2范数作为作动器、传感器的位置优化指标。Ding等[10]提出了一种基于特征值分解的空间H2范数计算方法,利用闭环空间H2范数分析了平板结构在空间分布扰动下的振动控制效果,最终依靠遗传算法来优化传感器、作动器位置。Liu等[11]提出空间H2范数,用以判断作动器在平面内的控制性能,并通过板的振动控制验证了优化方法的有效性。现有相关研究多使用状态空间模型计算目标函数,但对于实际系统,精确的模型通常难以获得;部分研究者针对实际结构研究了作动器、传感器的离散优化问题,陆洋等[12]和周刘彬等[13]分别通过遗传算法优化误差传感器位置以获得最优的主动控制效果,但未考虑作动器位置对控制效果的影响。

在主动隔振平台-壳体系统中,作动器、传感器位置按路径功率流控制进行配置。对于作动器和传感器位置已经确定的配置,在给定激励的条件下,只需从最高配置中选择部分作动器,即通过设定作动器的开、关状态从最高配置中进行优选。此优化问题可行域是离散的,本文将此问题转化为有约束的整数非线性规划,采用教与学优化(teaching and learning-based optimization, TLBO)算法[14]求解,以确定给定作动器集合中性能最优的组合。

1 系统动力学模型

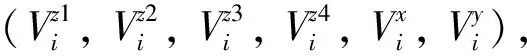
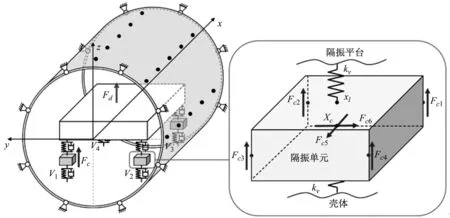
图1 舱段主动隔振系统示意图

表1 主动隔振平台-壳体耦合系统参数

本文采用基于频率响应函数的子结构综合法对耦合系统建模,得到圆柱壳、隔振单元、负载平台各子结构的频率响应函数后,进行综合,得到耦合系统的频域动力学方程。在此基础上,根据壳体的辐射声阻抗矩阵,计算壳体辐射声功率。

1.1 壳体模型

根据sanders壳理论,圆柱薄壳的中面应变与壳体位移u、v、w的关系为

(1)

(2)

壳体截面力与力矩由应力沿壳体厚度积分而得,截面力、力矩与壳体位移的关系在附录中给出。圆柱薄壳的应变能Us与动能Ts可表示为

(3)

(4)

式中,Nx,Nθ,Nxθ,Mx,Mθ,Mxθ为壳体的截面内力与内力矩。为使用能量方法对圆柱壳进行分析,需构造可行的位移函数表示变形过程中的位移。Xu等[15]提出将壳体位移u、v、w展开为傅里叶级数叠加辅助多项式的形式

(5)

(6)

(7)

式中：τ=0/1分别为对称/反对称模态;n为周向波数;m为傅里叶级数阶数;A,B,C为傅里叶级数待定系数;λm=mπ/Lx;Pal(x)为辅助多项式;a,b,c为辅助多项式待定系数。辅助多项式的形式在附录中给出。根据式(5)～式(7),壳体位移可以表示成形函数与对应系数的乘积

u(x,θ)=Puqu,v(x,θ)=Pvqv,w(x,θ)=Pwqw

(8)

式中：qu、qv、qw为傅里叶级数待定系数A,B,C与辅助多项式待定系数a,b,c组成的系数向量;Pu、Pv、Pw为傅里叶级数及辅助多项式组成的形函数。作用于系统的外力做功为力向量F与作用点位移向量XF的乘积Wf=FTXF。根据Hamilton原理,可得：

δ(Ts-Us+Wf)=0

(9)

将形函数Pu,Pv,Pw代入壳体动能与势能表达式(3),(4)并进行积分,整理可得：

(10)

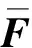
1.2 负载平台与隔振单元

耦合系统动力学模型中,隔振单元与负载平台均简化为有干扰力或控制力作用的刚体。刚体上任一点振动响应均可由质心振动响应和该点与质心的相对位置表示,而质心响应由刚体的受力情况决定。设刚体上坐标为(ae,be,ce)的一点受到激励力Fe=[Fx,Fy,Fz,Mx,My,Mz]T,则质心加速度响应Xc、刚体上坐标为(ar,br,cr)位置处的响应Xr可写为

Xc=

(11a)

(11b)

式中：ω为圆频率;M为刚体质量;Jx、Jy、Jz分别为刚体绕x,y,z轴的转动惯量。联立式(11a)与式(11b),刚体任一点的响应Xr可以通过激励力向量以及激励位置求出,以此可求得等效隔振单元的频率响应函数矩阵。隔振单元子结构的动力学方程包含隔振单元与壳体连接点、误差点、隔振单元与负载平台连接点的自由度,表示为

(12)

式中,下标l,e,h分别代表隔振单元与壳体连接点、误差点、隔振单元与负载平台连接点。类似地,负载平台子系统的频域动力学方程可写为

(13)

式中,下标d,h′分别代表干扰力作用点,负载平台与隔振单元连接点。

1.3 耦合系统动力学方程

本文通过基于频响函数的子结构综合方法构建隔振平台-壳体耦合系统动力学方程。隔振单元子结构、负载平台子结构的频域动力学方程由式(12)、(13)给出。根据式(10),圆柱壳动力学方程包含监测点自由度与隔振单元安装点的自由度,可写为：

(14)

式中：Hwl′为壳体监测点到隔振单元安装点的频响函数;Hl′l′为隔振单元安装点原点频响函数;Fl′为隔振单元子系统在安装位置处对壳体施加的作用力。对式(12)～(14)进行综合,其中

Fl=-Fl′=kv(Xl-Xl′)

(15a)

Fh=-Fh′=kv(Xh-Xh′)

(15b)

消去下标为l,l′,h,h′的自由度,耦合系统动力学方程可写为

(16)

式中：X=[XdXeXw]T为干扰力作用点,隔振单元误差点,以及壳体监测点的振动响应;Fd为干扰力;Fc为控制力;Hdd、Hed、Hwd分别为干扰力到干扰力作用点、误差点、监控点的频响函数;Hdc、Hec、Hwc分别为控制力到干扰力作用点、误差点、监控点的频响函数。

1.4 圆柱壳表面辐射声功率

考虑无限长圆柱障板中的有限长圆柱结构,将圆柱壳表面沿轴向x及周向θ离散为N个单元,各单元法向振速向量β以及辐射声压向量p可表示为向量形式

β=[β1β2…βN]T,

p=[p1p2…pN]T

(17)

结构的辐射声功率即为每个单元辐射声功率之和,可表示为声压与振速的乘积

(18)

式中：S为壳体辐射表面面积;表面声压p为辐射声阻抗与法向振速β的乘积,p=Zβ;Z为声阻抗矩阵,元素Zi,j表示第j单元的单位速度振动在i单元上引起的声压。Williams等[17]给出了无限大圆柱障板上有限圆柱面的辐射声阻抗矩阵,周瑶[18]给出了辐射声阻矩阵的数值计算方法,在数值计算过程中截断周向波数及轴向波数,并对轴向波数的积分域进行离散。辐射声阻抗矩阵为

(19a)

(19b)

(20)

由于辐射声阻抗阵Z为共轭对称矩阵,式(18)可改写为

(21)

式中,R为辐射声阻矩阵,R=(Z+ZH)/2。通过系统耦合动力学模型计算壳体表面声压,结合式(19)、(21),即可求得圆柱壳表面的辐射声功率。

2 配置优化

2.1 优化模型及优化准则

在主动控制系统中,干扰力产生的振动被误差传感器采集,驱动作动器产生使得误差点响应幅度相同、相位相反的作用力,从而抑制误差传感器位置处的振动。干扰力到误差点的传递通道称为干扰通道,控制力到误差点的传递通道称为控制通道。误差点与监测点的频率响应由干扰通道作用与控制通道作用线性叠加而得。令监测点数量为nw,干扰力作用自由度数目为nd。若在所有nc条控制通道中,给定控制通道数目na(开启na个作动器以及对应na个误差传感器),那么部分启用的控制系统对应的误差点与监测点响应表示为

(22)

式中：a为控制通道启用状态;ea为对应启用控制通道的误差点;ca为启用控制通道的作动器;s为控制通道关闭状态;es为对应未启用的控制通道的误差点;cs为对应未启用的控制通道的作动器;Heaca为na×na的控制通道频响函数矩阵;Head为na×nd的干扰通道频响函数矩阵;Hwca为作动器到监测传感器的频响矩阵,大小为nw×na。Xea、Xw、Fd与Fca分别为na×1、nw×1、nd×1、na×1的向量。理想情况下,可通过对控制通道频响函数矩阵求逆得到最优控制力,使得误差点响应为零,但在实际工程中,误差点振动很难被完全抑制。在本文作动器的优化评估中,假定控制力使误差点振动幅值下降20 dB,则对应的控制力为理想控制力的90%,即

(23)

将控制力代入监测点响应表达式,可得

(24)

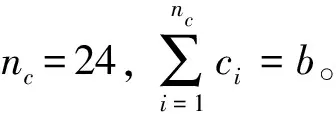
(25)

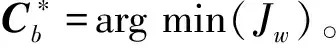
(26)

此优化问题的可行解数目为

(27)

2.2 优化算法

式(26)描述了一个非凸、高维、可行域离散的优化问题,此类优化问题一般通过启发式优化算法求解。TLBO算法是一种新颖的启发式算法,Rao等在2011年提出了标准TLBO求解范式,Chen等在标准求解范式基础上改进了初始分布的多样性,曹丙花等[19]则在初始种群多样性、局部最优值跳出等方面对TLBO进行了改进。本文使用融合了自适应局部最小值跳出机制与模糊函数的改进整数TLBO方法求解作动器配置优化问题,具体步骤如下：

(1) 种群初始化。给定种群中个体数目Npop,种群中个体在可行空间中随机采样。

(2) 教学阶段。在第t轮迭代中,首先计算种群中所有个体对应的f(C),得到最优个体Ckbest,t并指导其余个体进行更新,更新方式为

(28)

(29)

(3) 互学阶段。此阶段随机选取种群中一对个体CP,t与CP,t并比较其适应度函数,令适应度更低的个体向高适应度个体靠拢,可表示为

(30)

(31)

式中：rand为(0,1)中的随机数;c‴j,k,t为第t轮迭代后的最终得到的第k个状态向量的第j维元素。这样,改进后的TLBO算法可应用于求解0-1非线性规划问题。

3 数值仿真

考虑负载平台上存在轴系、发电机、柴油机等旋转机械带来的激励力,给定激励力位于负载平台质心,沿横向与垂向施加单位力,且激励的相位差为90°。本文考虑两种激励工况,分别为：

工况一 0～300 Hz宽带单位激励力

工况二 50 Hz与100 Hz线谱激励,幅值为1

(32)

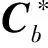
(33)

辐射声功率级=10lg(Wrad/Wref)

(34)

式中：βref为均方振速参考值,βref=10-9m/s;Wrad为辐射声功率参考值,Wref=10-12W。本文采用9×16的网格对壳体均方振速及辐射声功率进行计算。

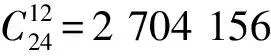
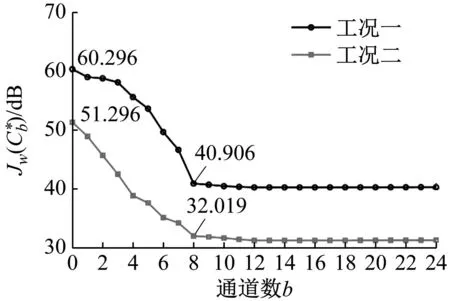
图2 各作动器数最优组合对应目标函数值

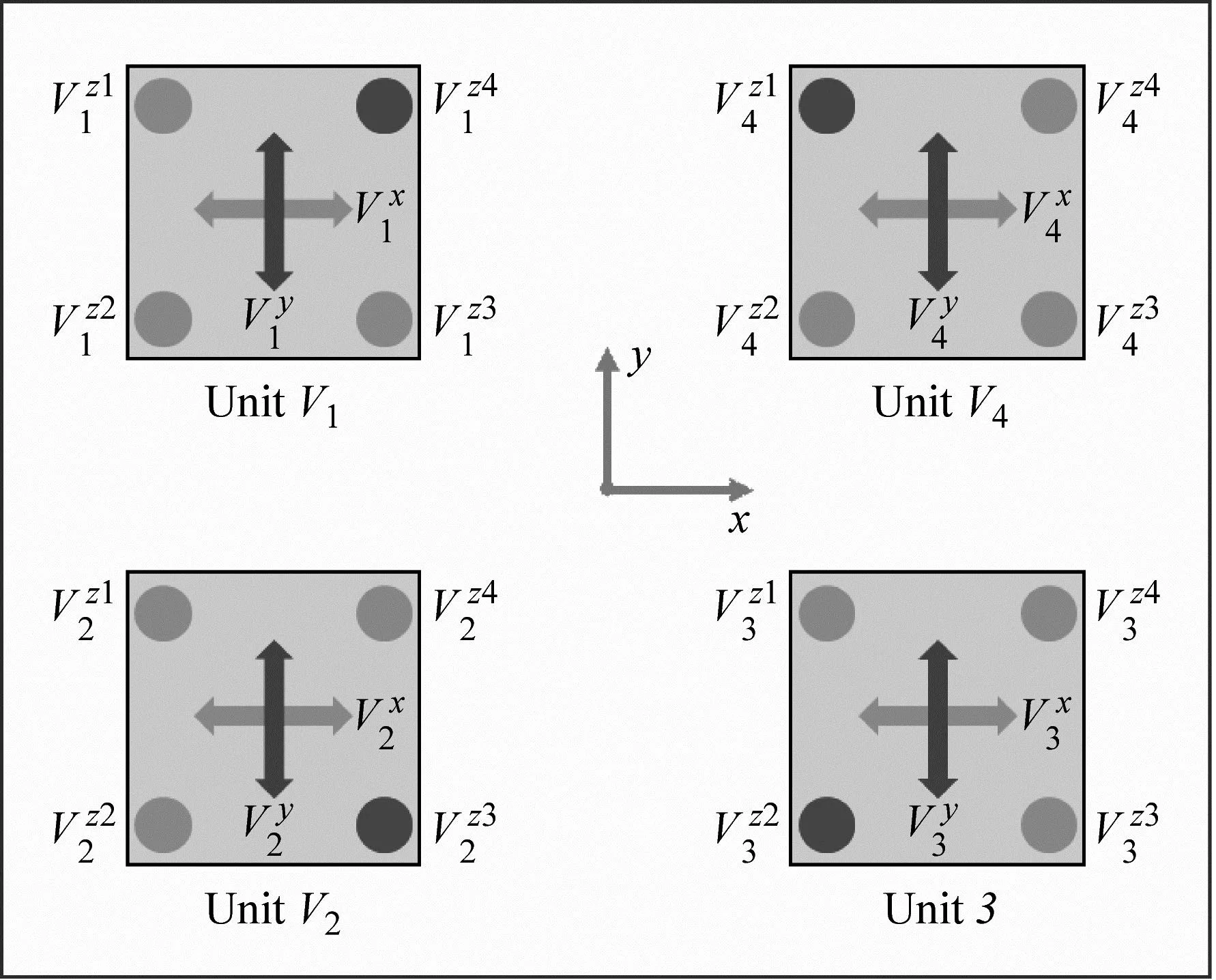
(a) 八作动器最优配置(工况一)

(b) 八作动器最优配置(工况二)

图4给出了工况一最优作动器配置组合对应的壳体均方振速级和辐射声功率级。图4中b=8、12、24的曲线几乎重合,对应的RMS也相差无几。相较于无控状态b=0的响应曲线,b=8对应的均方振速和辐射声功率几乎在全频段下降20 dB。

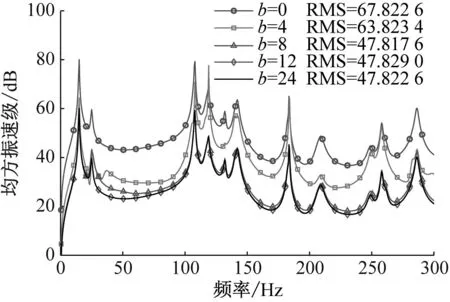
(a) 壳体均方振速级

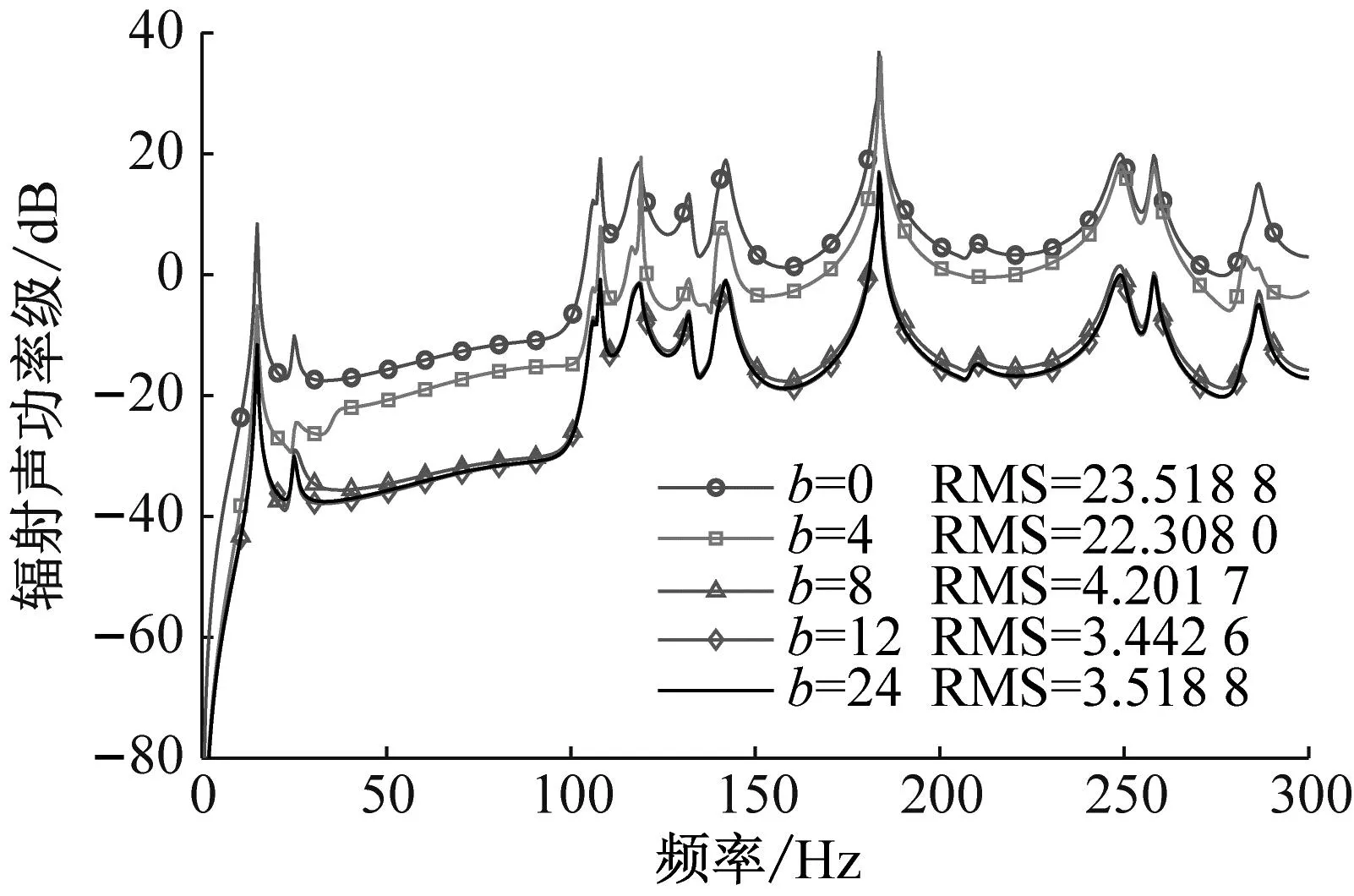
(b) 壳体辐射声功率级

(a) 50 Hz,b=0,均方振速级=49.13 dB

(c) 50 Hz,b=24,均方振速级=29.13 dB

(d) 100 Hz,b=0,均方振速级=58.75 dB

(e) 100 Hz,b=8,均方振速级=39.51 dB

(f) 100 Hz,b=24,均方振速级=38.75 dB

图5 最优控制通道配置对应壳体振速幅值(工况二)

此外,并非所有激励工况都只需要8通道即可得到较好的振动控制效果,例如在负载平台质心轴向单位激励力作用下,需要至少12通道的最优通道组合才可得到20 dB的振动抑制。更复杂的激励工况将会需要更多的通道数,由于篇幅限制此处不作展开。

4 结 论

本文针对主动隔振平台-壳体系统的控制问题,建立了耦合系统动力学模型,计算得到主动控制系统的控制通道频响与干扰通道频响,以及干扰力、控制力到壳体监测点的频响;提出了作动器配置优化方法,将监测点响应作为优化问题的目标函数,在给定作动器数目的约束下,通过TLBO对此0-1非线性规划问题求解。数值仿真验证了优化方法的有效性,结果表明,对于本文给出的激励工况,无需开启所有作动器,只需在主要通道施加控制,即可有效抑制壳体振动与声辐射。

此外,即使是相同的激励形式,不同频率对应的最优通道配置也不尽相同。在实际工程中,若能测得激励源频率、幅值、相位等特性,则可根据激励源特性优化对应的控制通道组合,取得更好的振动抑制效果。

附录A

截面力、力矩与壳体位移的关系

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)

(A.6)