基于ARMAV模型和J-散度的结构损伤识别

李 孟, 郭惠勇

(1. 重庆大学 土木工程学院, 重庆 400045;2. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045)

土木工程结构在服役过程中会受到自身材料老化和自然环境的影响,导致局部区域发生损坏。为了避免因为损伤的积累而导致结构失效造成的人员财产损失,对结构进行健康监测是必要的[1]。

基于振动的损伤识别方法是结构健康监测的一个重要类别[2-3],其基本原理是,损伤会引起结构的物理特性发生改变,同时该变化会反映在结构输出的动力响应中,通过分析损伤前后结构振动特性或者动力响应的变化识别结构损伤。经过长久的发展,基于振动的损伤识别技术可以划分成基于模态参数的方法和基于时域响应的方法两大类[4]。基于模态参数的方法在实践中难以获取结构模态的完整信息,对轻微损伤和局部损伤不敏感[5]。相比之下,基于时域响应的方法信息获取方便快捷并且节约成本,其中基于时间序列分析的损伤识别方法以其可操作性强、对结构局部损伤的敏感性强等方面的优势成为了近年来损伤识别领域研究的热点[6-9]。

时间序列模型的参数和特性包含了大量对损伤敏感的特征信息[10],因而可以用作辨识结构损伤及其位置。Nair等[11]将自回归滑动平均(autoregressive moving average, ARMA)模型的前三个自回归系数作为损伤特征向量,并基于损伤前后该特征的统计差异构造损伤指标,四层框架结构仿真结果表明,所提算法能够辨识不同程度损伤。Zheng等[12-13]利用ARMA模型和自回归(autoregressive, AR)模型的距离度量作为损伤识别指标,五层层间剪切结构数值模拟结果表明,所提算法能够定位结构损伤。刘纲等[14]基于向量自回归(vector autoregressive, ARV)模型和马氏距离构造损伤特征值,结合受试者工作特征(receiver operating characteristic, ROC)曲线下的面积定位结构损伤,最后用数值模型和两层钢框架模型试验加以验证。张玉建等[15]将AR模型和外部输入相结合建立ARX模型(autoregressive model with exogenous input)用于损伤检测和定位,并用数值模型验证所提方法的有效性。现有研究的数值模拟算例多数是简单的多自由度结构模型,缺乏真实结构的验证,并且建立的损伤判别指标不够直接。因此,需要在对损伤特征指标的构造以及指标在真实结构上的应用这两方面进行更多的研究。

为此,本文在以往基于时间序列分析的损伤识别方法研究的基础上,提出用预处理后的加速度响应直接建立向量自回归滑动平均(vector autoregressive moving average, ARMAV)[16]模型,从中提取损伤特征信息,结合J-散度距离函数构造损伤特征指标从而实现损伤诊断的方法。该方法无需对采集到的响应数据进行模态分解或者频域相关的计算,其准确性和适应性首先通过三层框架结构的试验数据加以验证,然后进行转播塔模型试验研究来验证其在层间刚度变化的塔式结构中的有效性。

1 ARMAV模型

1.1 ARMAV模型基本理论

多维ARMA模型,称为ARMAV模型,在工程应用中具有更广泛的应用前景[17]。l维ARMA(n,m) 模型,即ARMAV(n,m;l) 模型通常表示为

(1)

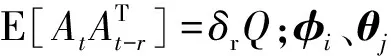
(2)

由式(2)可知,ARMAV模型不仅能反映单个时序内部数据先后之间的统计联系,还能反映不同时序之间相互影响的关系。

1.2 ARMAV模型建模

本文采用长自回归计算残差法和最小二乘估计法建立ARMAV模型,其主要步骤如下：

步骤1将预处理后的观测时序{x1,t,x2,t,…,xl,t}代入式(1),设定阶数p的初值,建立ARV(p;l) 模型,即ARMAV(p, 0;l) 模型。令：

yk=[xk,p+1xk,p+2…xk,N]T

(3)

εk=[ak,p+1ak,p+2…ak,N]T

(4)

γk= [φk,1,1φk,1,2…φk,1,p|…|φk,2,1φk,2,2…φk,2,p|…|φk,l,1φk,l,2…φk,l,p]T

(5)

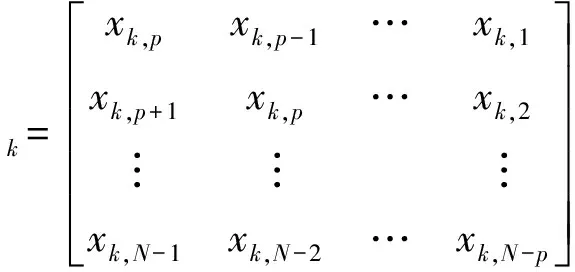
(6)

式中：k=1,2,…,l,下文中的k取值相同;γk是长度为p×l的参数向量。因此ARMAV(p, 0;l) 模型的矩阵形式可以表示为[17]

Y=WΓ+ε

(7)

式中：Y=[y1y2…yl];W=[ϖ1ϖ2…ϖl];Γ=[γ1γ2…γl];ε=[ε1ε2…εl]。

式(7)中的Y和W均已知,可采用最小二乘估计法计算模型的参数矩阵Γ

Γ=(WTW)-1WTY

(8)

步骤2用残差平方和准则检验模型的适用性,若模型不适用,则令p=p+1返回步骤1。第k个标量模型的残差平方和Sk的算式为

(9)

式中,残差序列εk=yk-Wγk。当模型的阶数由低至高后,Sk急剧减小,则表明该低阶模型不适用。

步骤3根据长自回归计算残差估计法,将残差ε作为ARMAV(n,m;l) 模型滑动平均部分的观测值,并设置初始阶数n和m(通常令m=n-1),建立ARMAV(n,n-1;l) 模型,重复步骤1和步骤2直至模型适用则完成建模。

2 损伤指标和识别流程

时间序列模型将结构的特性与结构服役状态的所有信息凝聚其中,依据时序模型的参数和特性构造损伤判别函数是研究时序方法在结构损伤识别中应用的关键。

2.1 J-散度

将结构损伤前后的状态分别定义为参考状态和待检验状态,为了量化两个状态下采集到的结构动力响应之间的差异,引入信息论中的Kullback信息量[18]。时间序列方法中的Kullback距离函数定义为

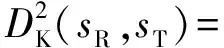
(10)

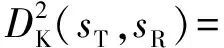
(11)

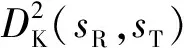
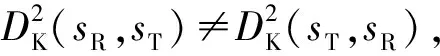
(12)

2.2 基于ARMAV模型和J-散度距离的损伤识别

时序模型的自回归参数反映结构的固有特性,模型的残差方差与结构的输出特性紧密相关。因此,提出利用ARMAV模型自回归部分的参数以及模型的残差方差作为损伤敏感信息,然后将其代入到能够描述损伤前后信息差异的判别函数J散度距离,从而构建损伤特征指标JD,实现结构的损伤识别。

使用参考状态下的l元时序向量{Xt}R建立参考模型,使用待检验状态下的l元时序向量{Xt}T建立待检验模型。由于模型参数的重要性不同,为了提高计算速度,选择能够反映结构状态的主要特征参数。提取式(2)中自回归项系数φi主对角线上的元素组成长度为n×l的向量f

f=[φ1,1,1φ1,1,2…φ1,1,n|…|φ2,2,1φ2,2,2…φ2,2,n|… |φl,l,1φl,l,2…φl,l,n]T

(13)

为了符合矩阵乘法维数匹配原则,计算式(13)中各部分的均值,组成长度为l的损伤特征向量φ,φ=[φ1φ2…φl]T,其中φk的形式如下

(14)

由式(14)可得到损伤前后两个状态下的φR和φT,再由式(12)即可得到基于ARMAV模型和J-散度距离的损伤特征指标JD

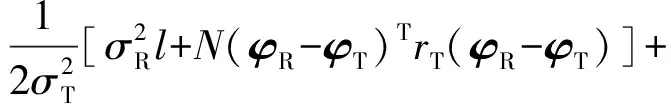
(15)

计算每一子结构的损伤特征指标JD,结构损伤位置对应的JD值最大,从而定位结构的损伤。

2.3 基于ARMA模型倒谱距离的损伤识别

为了验证JD指标识别结构损伤的准确性和适用性,引用传统的基于ARMA模型倒谱距离指标对结构损伤进行诊断。倒频谱最早由Bogert等提出,用于进行回声检测[20]。Zheng等将传统的基于ARMA模型倒谱距离理论应用于土木工程的结构损伤检测领域,即两个ARMA模型间的倒谱距离可简化为等效的两个AR模型之间的倒谱距离,结构损伤前后两个AR模型N(1)和N(2)之间的倒谱距离指标ICM( cepstral metric indictor,CMI) 可以表示为

(16)

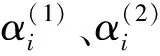
2.4 运用ARMAV模型和J-散度距离进行损伤识别的流程

基于本文方法辨识结构损伤的主要步骤如下,流程图如图1所示。

(1) 采集每个子结构在参考状态和待检状态下对应的加速度响应数据,首先对数据进行预白化处理,然后对其进行平稳性检验,将非平稳数据进行差分处理。

(3) 计算损伤特征指标JD,结构损伤位置所在的子结构对应的JD值最大,由此完成结构健康诊断。

3 三层框架试验验证

3.1 试验介绍

采用美国阿拉莫斯(Los Alamos)实验室提供的三层框架结构损伤经典试验数据[21]验证本文所提方法的有效性。如图2所示,试验模型由铝柱(17.7 cm×2.5 cm×0.6 cm)和铝板(30.5 cm×30.5 cm×2.5 cm)通过螺栓连接而成;模型安装在沿铝板长度方向滑动的单向导轨上,通过激振器沿底层铝板长度方向的中心线对结构施加带宽为20～150 Hz的白噪声激励;底部铺垫了一层硬质泡沫以减少外界扰动对测量结果的影响。加速度计型号为PCB 336C,安装在激振器对侧每层楼板的中心位置,由下至上编号为通道1～通道3。采用Dactron Spectrabook数据采集系统,数据采样频率设置为320 Hz。

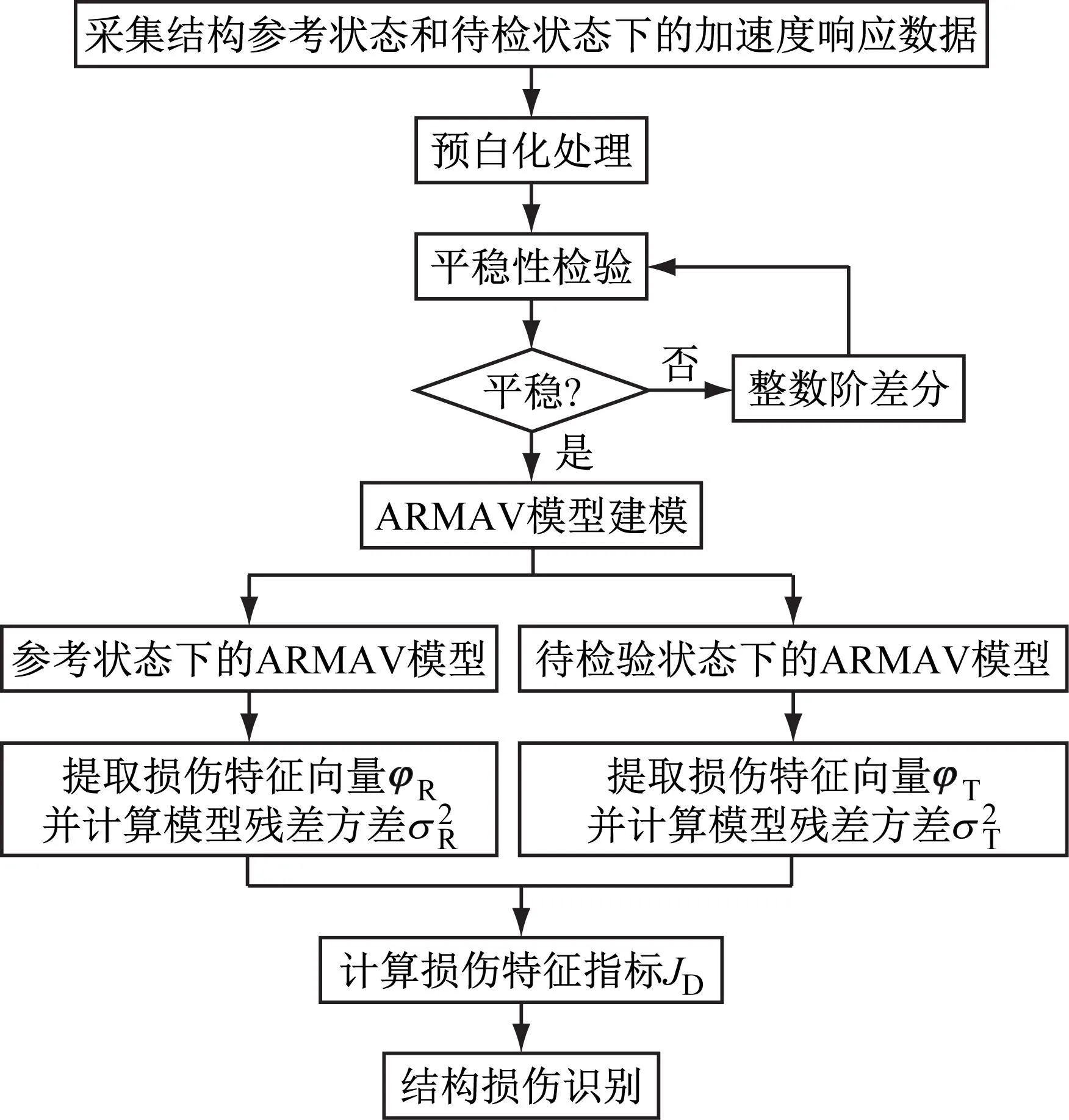
图1 基于ARMAV模型和J-散度的结构损伤识别流程图

图2 三层框架试验模型及加载装置

试验工况如表1所示,工况1为结构未受损时的基准工况;工况2～工况7通过改变柱截面尺寸来模拟结构因损伤导致自身刚度的下降,其中的工况5～工况7通过增加小刚度柱子的数量来模拟结构受损程度的加大。

表1 三层框架模型的试验工况

3.2 损伤识别

以工况2为例,损伤前后通道1～通道3加速度响应数据如图3所示,每个通道均采集了8 192个加速度响应数据。取预处理后的前8 190个数据划分成10段建立ARMAV模型。设定阶数p的初始值为3,对数据拟合适用的ARV(p; 10) 模型。得到满足适用性的模型ARV(3;10),计算其残差ε,并从n=2,m=1逐步升阶拟合ARMAV(n,m;10) 模型。最终选定ARMAV(2,1;10) 模型,并根据模型的参数和残差方差计算损伤特征指标JD。本文用作对比的倒谱距离指标CMI中的模型阶数p(1)和p(2)统一取4。

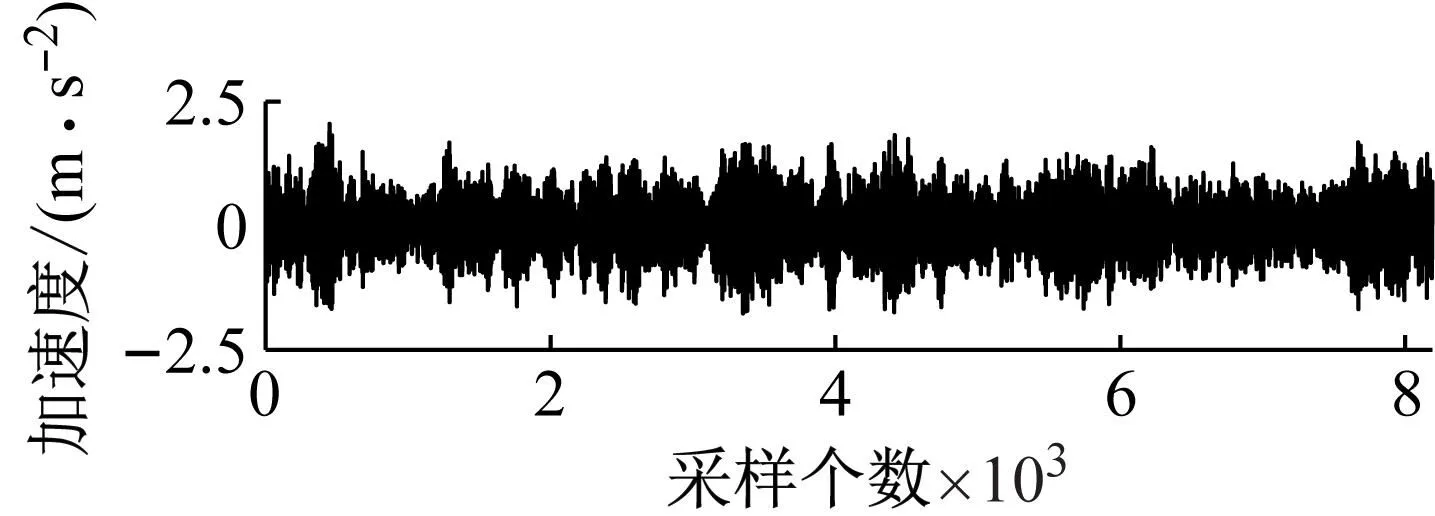
(a) 通道1

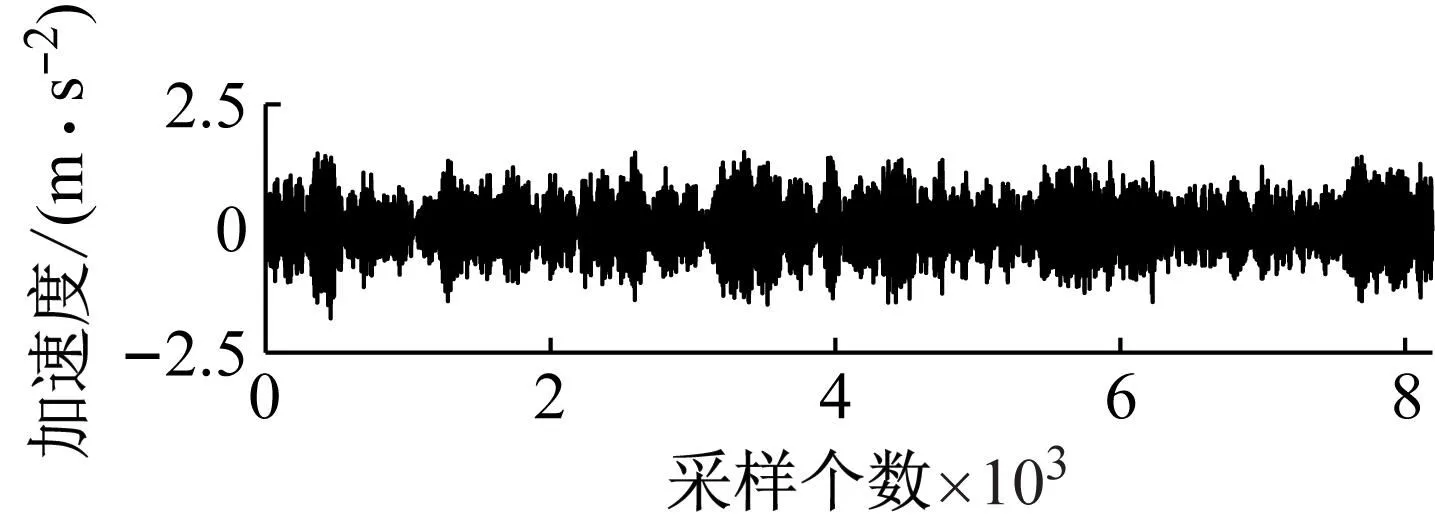
(b) 通道2

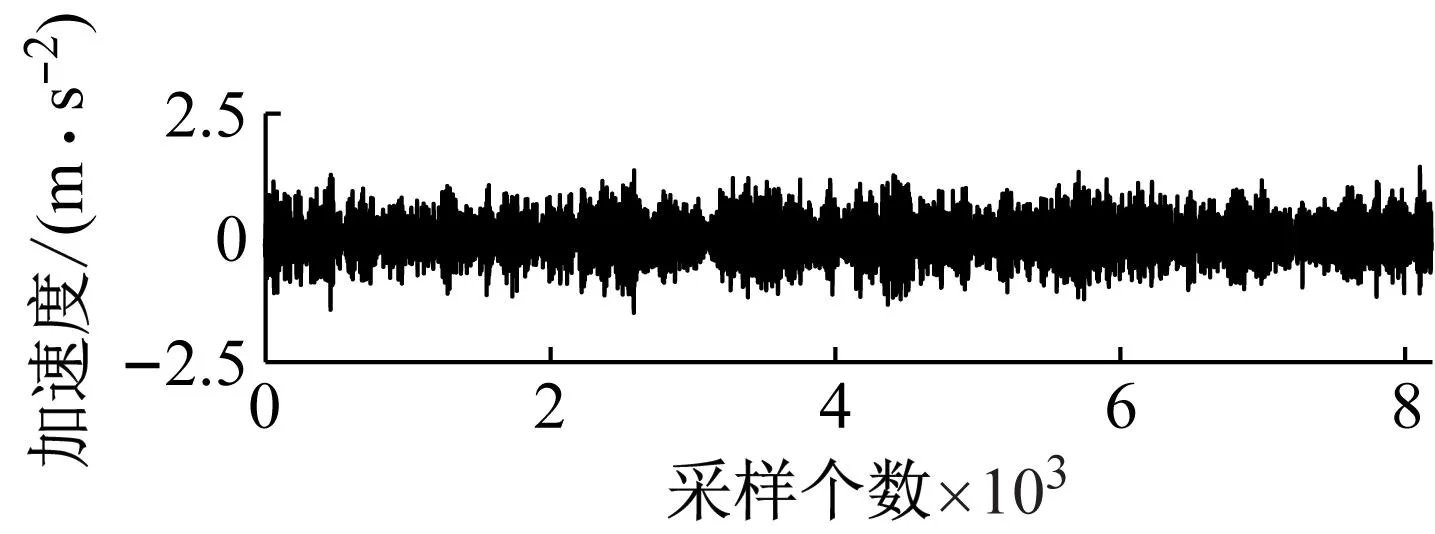
(c) 通道3

为了更好地评价指标,将JD和CMI两个指标分别按照式(17)进行归一化处理

(17)

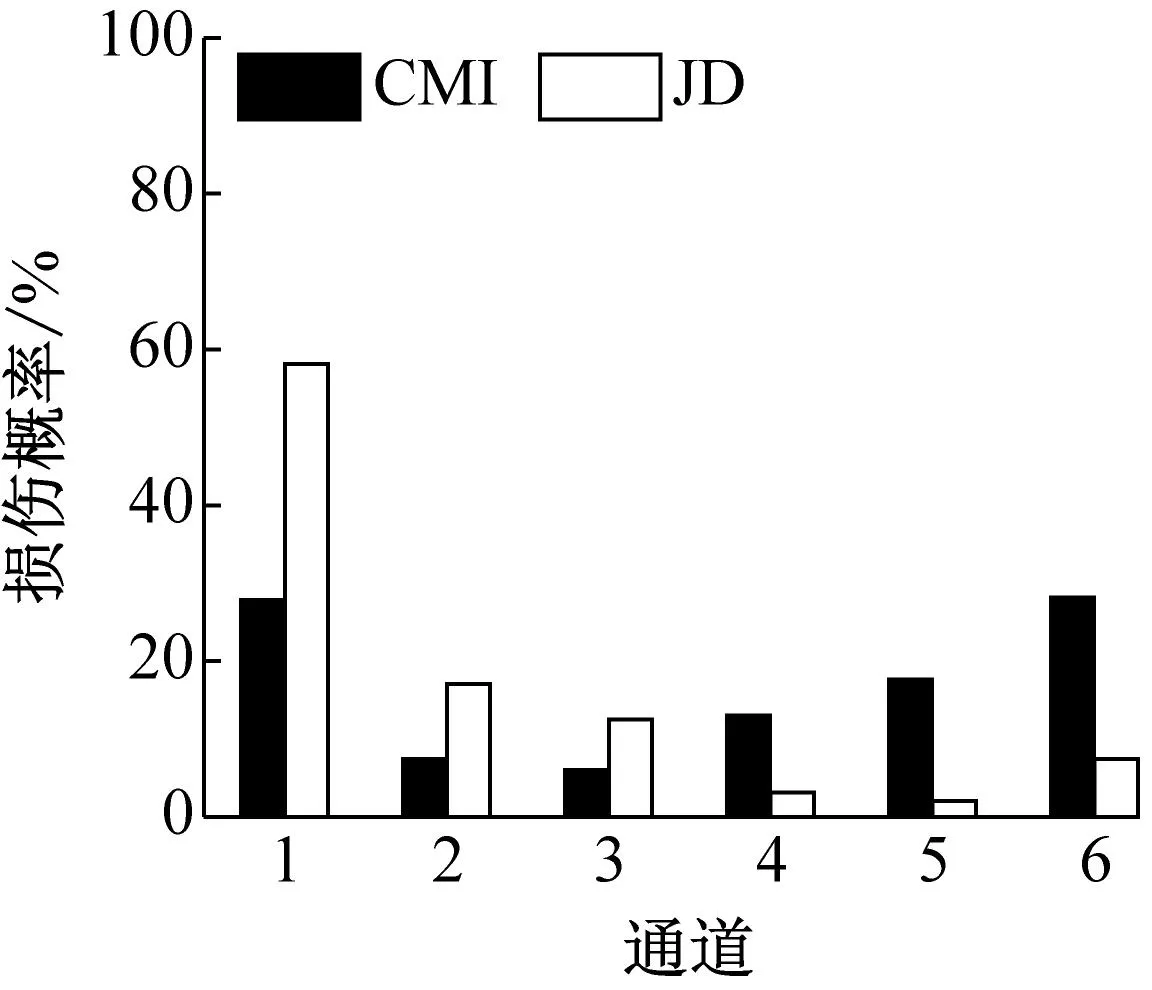
用通道的位置定位结构损伤,见图2。第一层位于通道1的下侧,第二层位于通道1和通道2之间,第三层位于通道2和通道3之间,识别结果如图4所示。设定通道编号为s,结构损伤识别的依据为：① 当s>2,若通道s与通道s-1的指标值之和大于50%,则判定损伤发生在第s层;② 当s=2,在通道2与通道1的指标值之和大于50%的情况下,若通道1的指标值是通道2指标值的2倍及以上,则判定损伤发生在第1层,否则判定损伤发生在第2层。

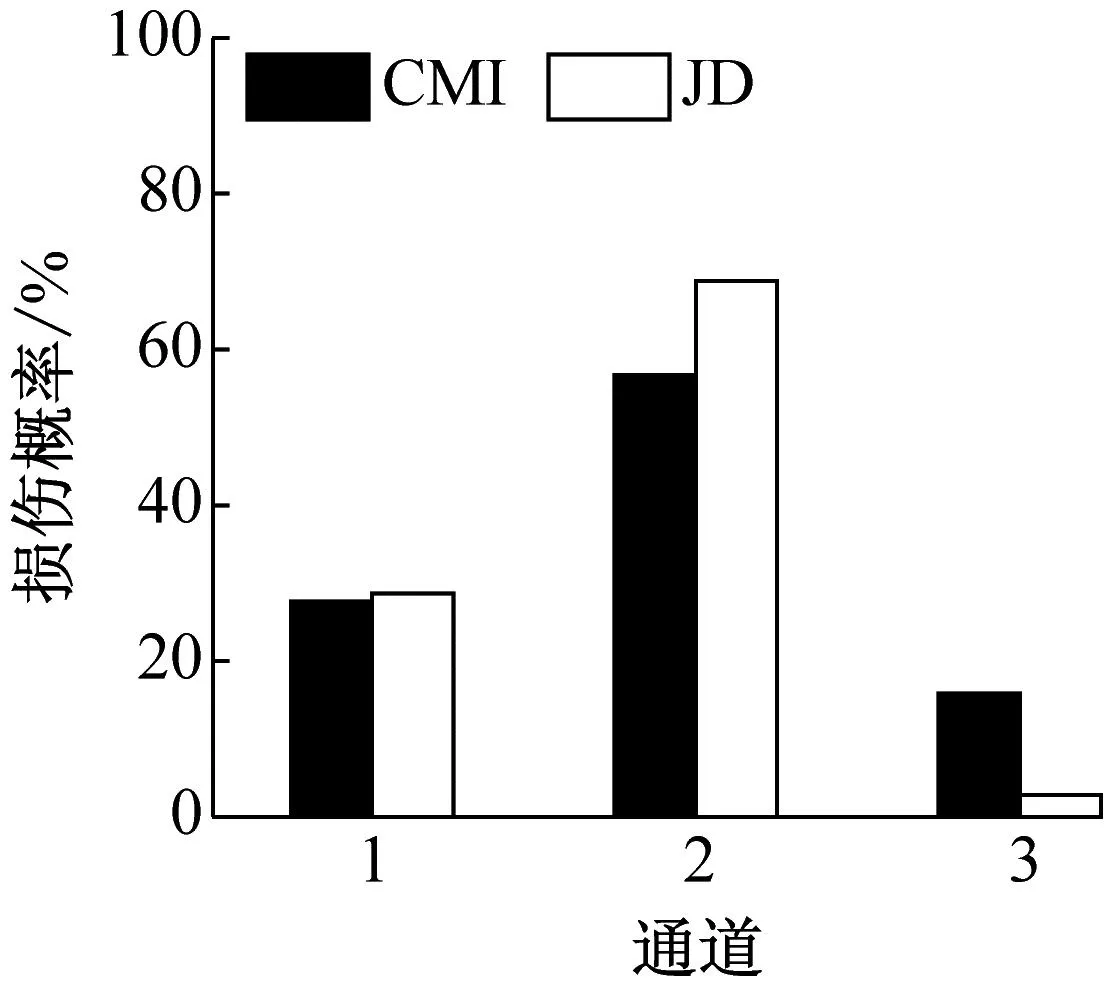
(b) 工况3

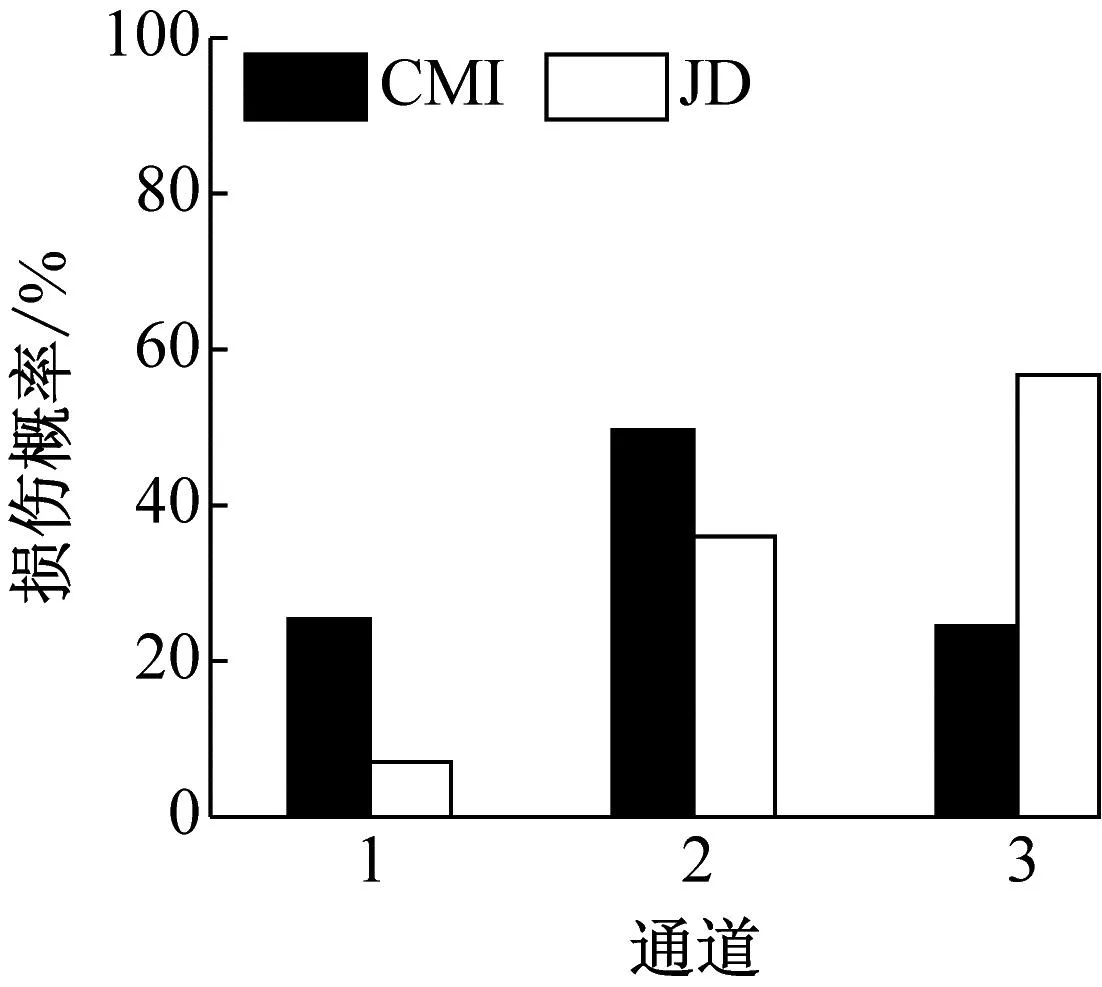
(c) 工况4

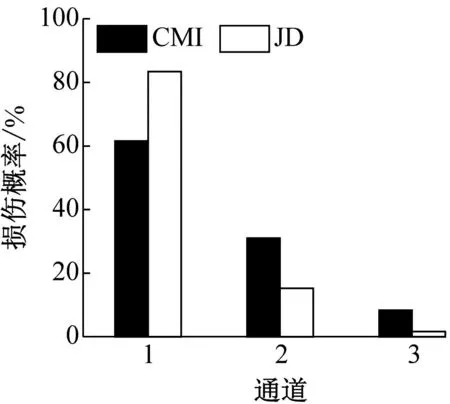
(d) 工况5

(e) 工况6

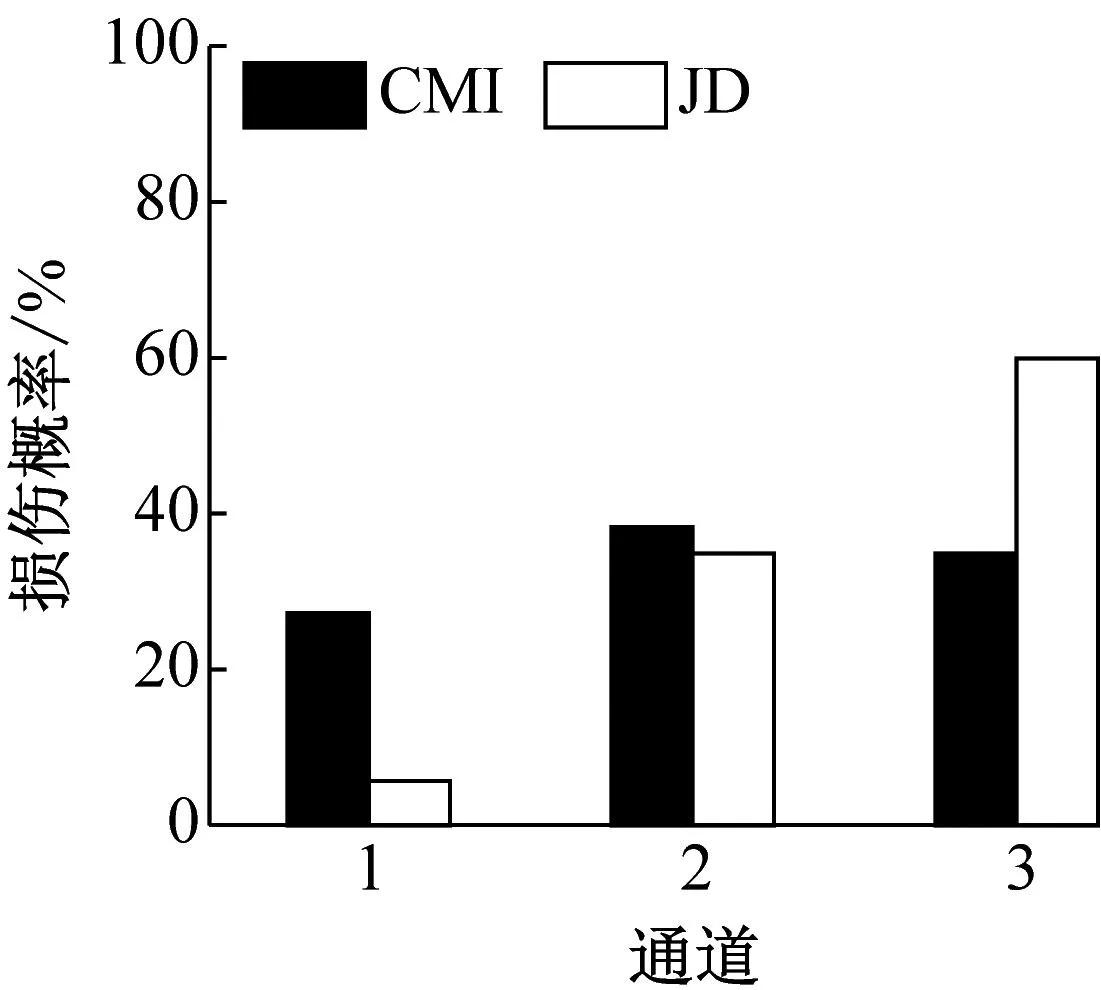
(f) 工况7

图4(a) 和图4(d) 显示,通道1的损伤概率显著高于通道2和3,表明JD指标和CMI指标均能辨识工况2和工况5中的损伤源最有可能位于第一层,与实际损伤位置相符。但以工况2为例,由JD值计算得到的通道1的损伤概率分别为通道2和3的4.57倍和50.15倍;由CMI值计算得到的通道1的损伤概率分别为通道2和3的2.22倍和4.35倍,表明JD指标对损伤的定位更精准。

图4(b) 和图4(e) 显示,损伤源最有可能位于通道1和2之间,即损伤最有可能位于第二层,表明JD指标和CMI指标均能辨识工况3和工况6中的损伤源所处位置。但以工况3为例,由JD值计算得到的通道1和2的损伤概率均高于由CMI值得到的,而由CMI值计算得到的通道3的损伤概率是对应JD值的5.93倍,表明JD指标错误判别的概率更低。

图4(c) 和图4(f) 显示,由JD指标计算得到的通道2和3的损伤概率比通道1的大得多,表明损伤源最有可能位于通道2和3之间,即损伤最有可能位于第三层,与实际情况相符;但CMI指标难以判别损伤甚至出现了误判,表明JD指标的损伤识别能力更高。综上,本文所提出的损伤识别方法能够更有效并且更精准地定位结构损伤。

4 转播塔模型试验研究

4.1 试验介绍

为了进一步验证本文提出的方法的适用性,进行了转播塔模型损伤识别试验研究。如图5(a) 所示,试验模型的主框架由圆钢管柱(φ10×2 mm)和圆形截面钢横梁(φ6 mm)通过焊接连接而成;节点板采用厚4 mm、长30 mm的方形钢板,通过焊接连接在柱与横梁的交接处;水平支撑和竖向支撑均采用边长为6 mm的方形截面铝材,通过螺栓连接的方式连接在节点板上;模型底部与振动台固结。柱、横梁和支撑在节点板处的连接详图见图5(b)。

模型尺寸以及加速度计布置位置如图6所示,将模型划分为8层,由于振动台是单轴振动,因此只采集与振动方向(水平y向)相同的加速度响应数据;根据损伤工况将传感器布置在结构第1层～第6层的节点板上,由下至上编号为通道1～通道6,传感器型号为1A206E,具体参数如表2所示。选用的采集设备为东华DH5927 N动态信号测试分析系统,数据采样频率设置为250 Hz。通过振动台施加由巴特沃斯低通滤波器处理后的白噪声激励来模拟结构在自然激励下的振动,白噪声的带宽为0～50 Hz。

图5 转播塔试验模型

Fig.5 Test model of relay tower

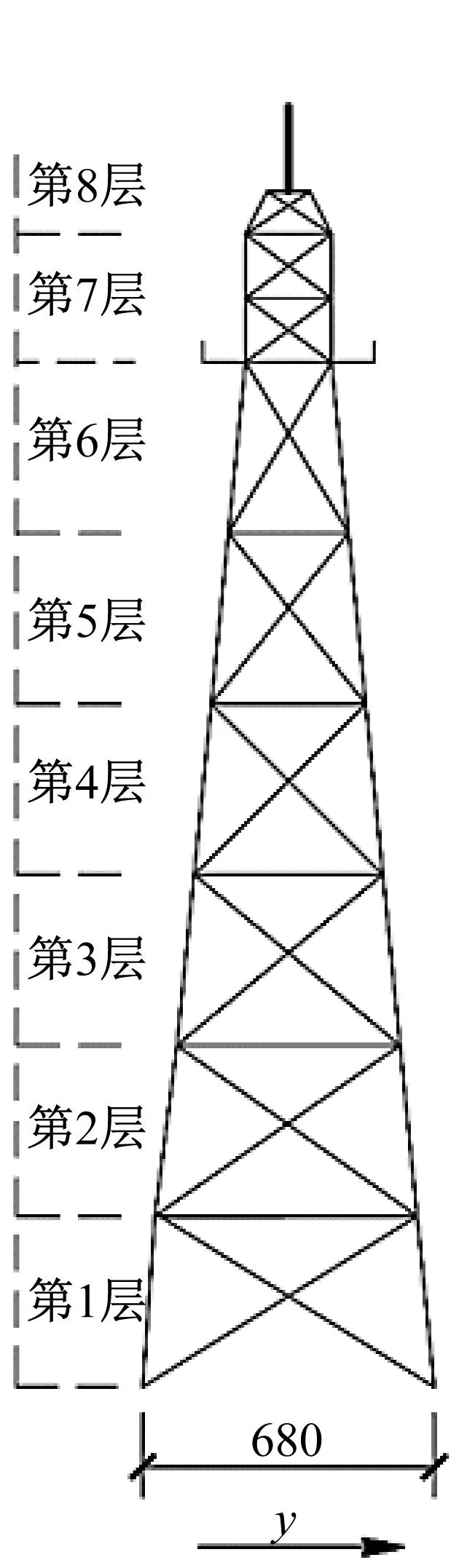
图6 转播塔模型几何尺寸及传感器布置(mm)

试验是通过拆除与振动方向同向的竖向支撑来模拟真实结构在服役过程中因损伤而导致自身刚度降低的情况。由于所拆除斜撑的质量在模型总质量中的占比很小,因此不考虑由拆除斜撑引起的结构质量的变化。试验工况如表3所示。工况1为无损伤工况;工况2～工况4通过拆除结构中位于指定层y向的竖向支撑来模拟损坏;工况5～工况6是在结构出现损伤的同时在第7层的平台处放置0.6 kg的质量块来模拟结构服役过程中的质量变化对识别结果的影响。附加质量的设置如图5(c) 所示。

表2 传感器通道参数和布置方案

表3 转播塔模型的试验工况

4.2 损伤识别

为了消除由振动台启动和停止带来的噪声对测量结果的影响,对由传感器获得的加速度时间序列做截断处理,取后5 000个作为损伤识别研究的原始数据,以工况2为例,建模用的通道1～通道6的原始数据如图7所示。将5 000个数据划分成10段建立ARMAV(14,13;10) 模型,计算各子结构的JD指标并将其进行归一化处理,得到的损伤识别结果如图8所示。

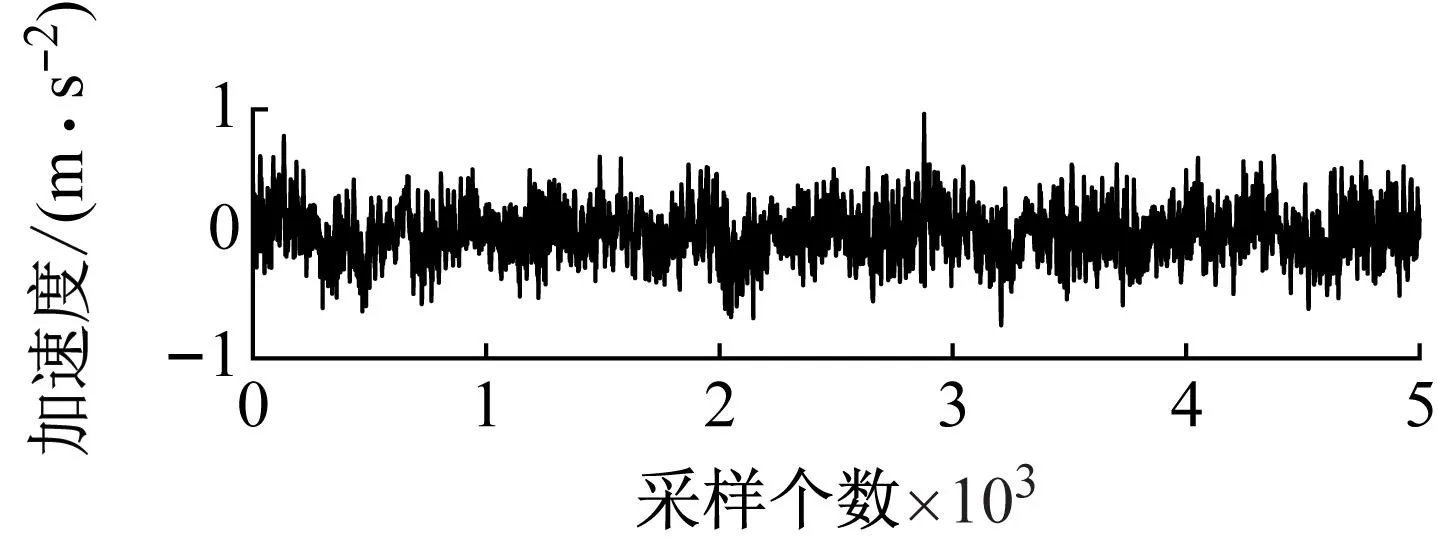
(a) 通道1

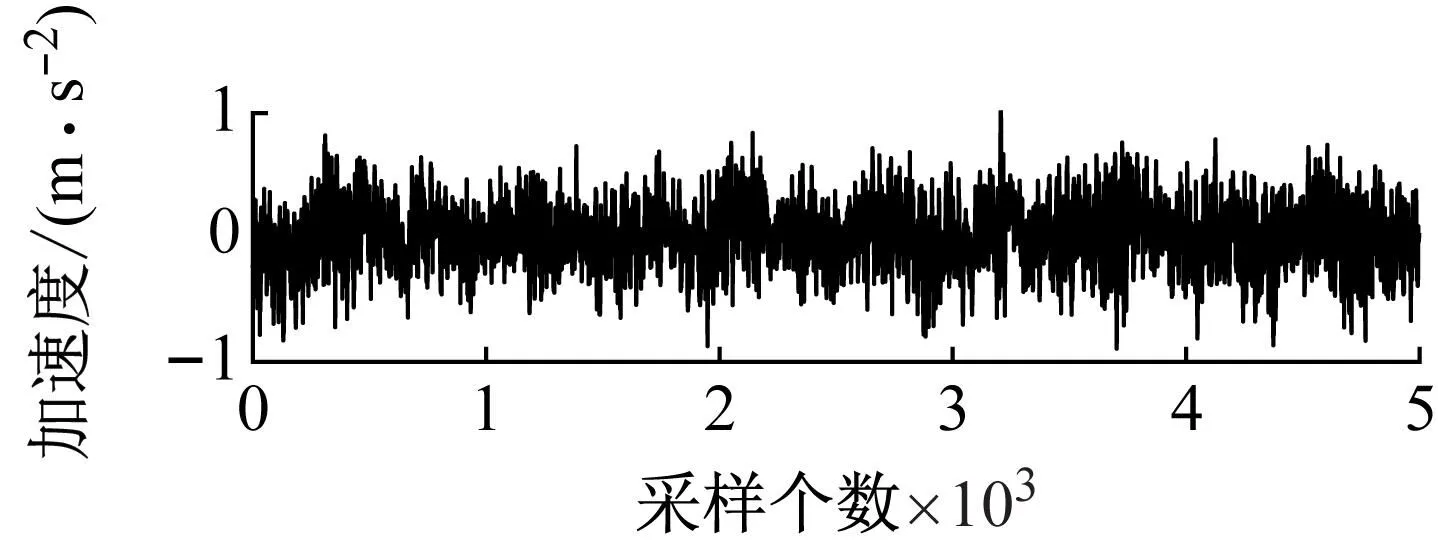
(b) 通道2

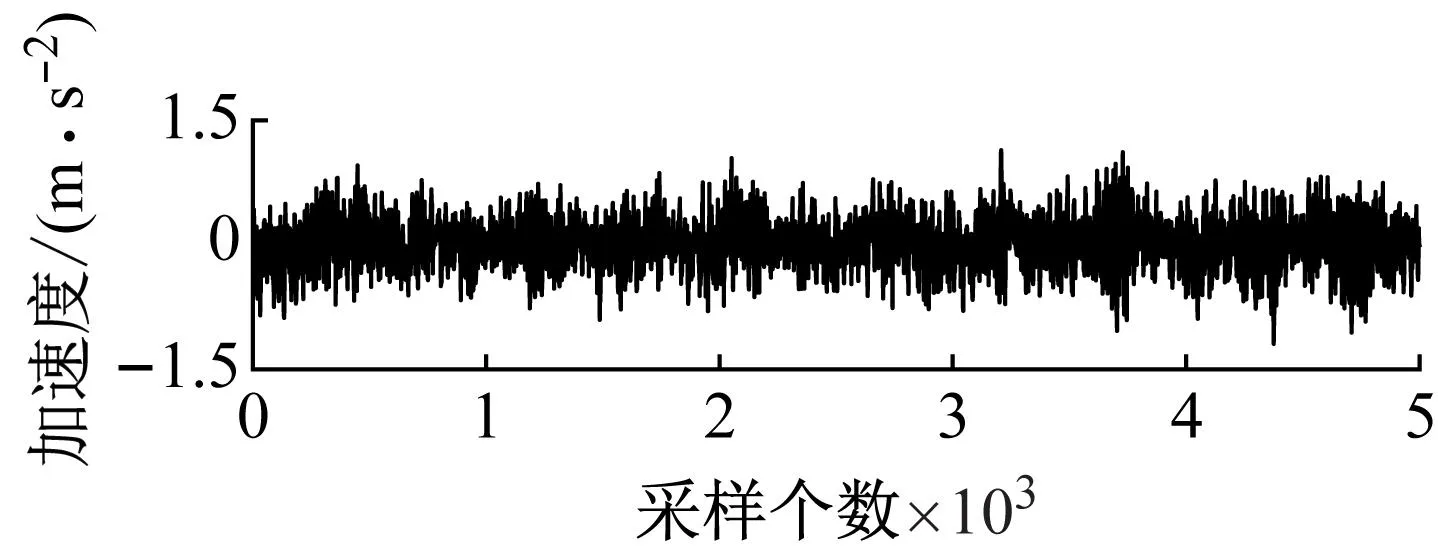
(c) 通道3

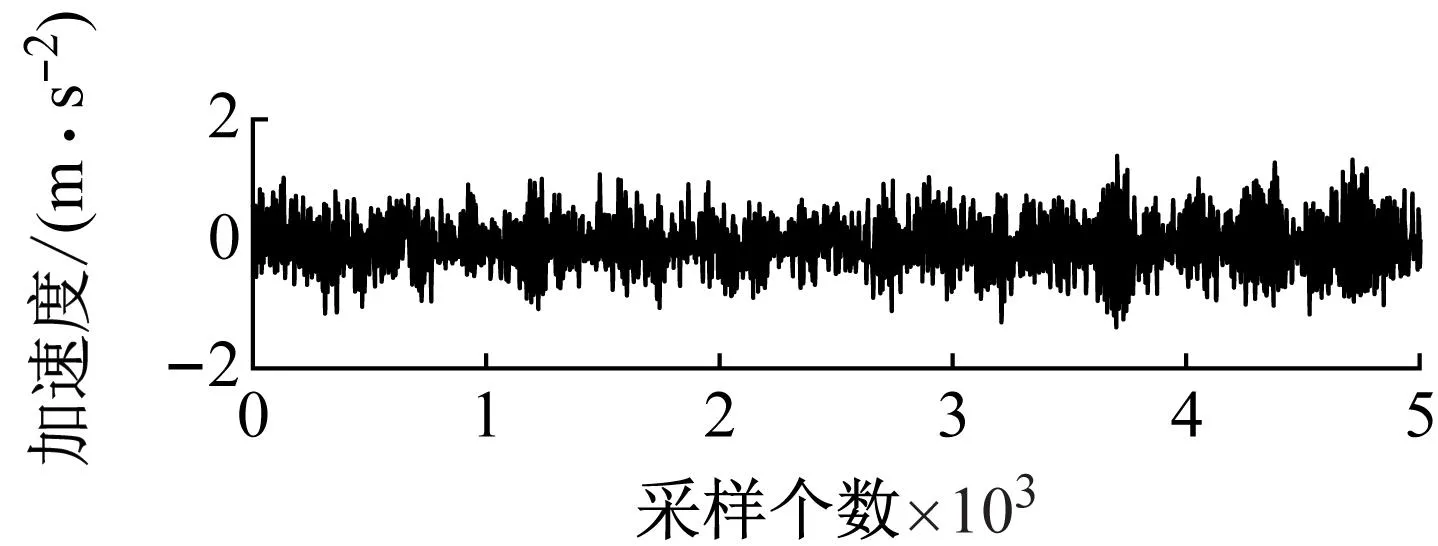
(d) 通道4

(a) 工况2

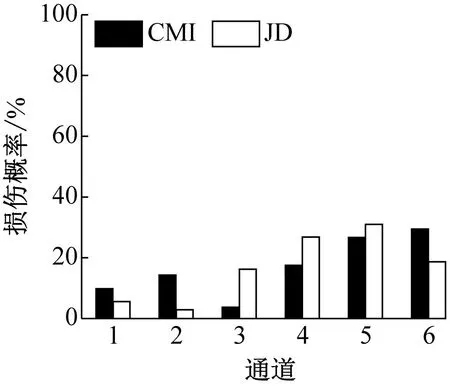
(b) 工况3

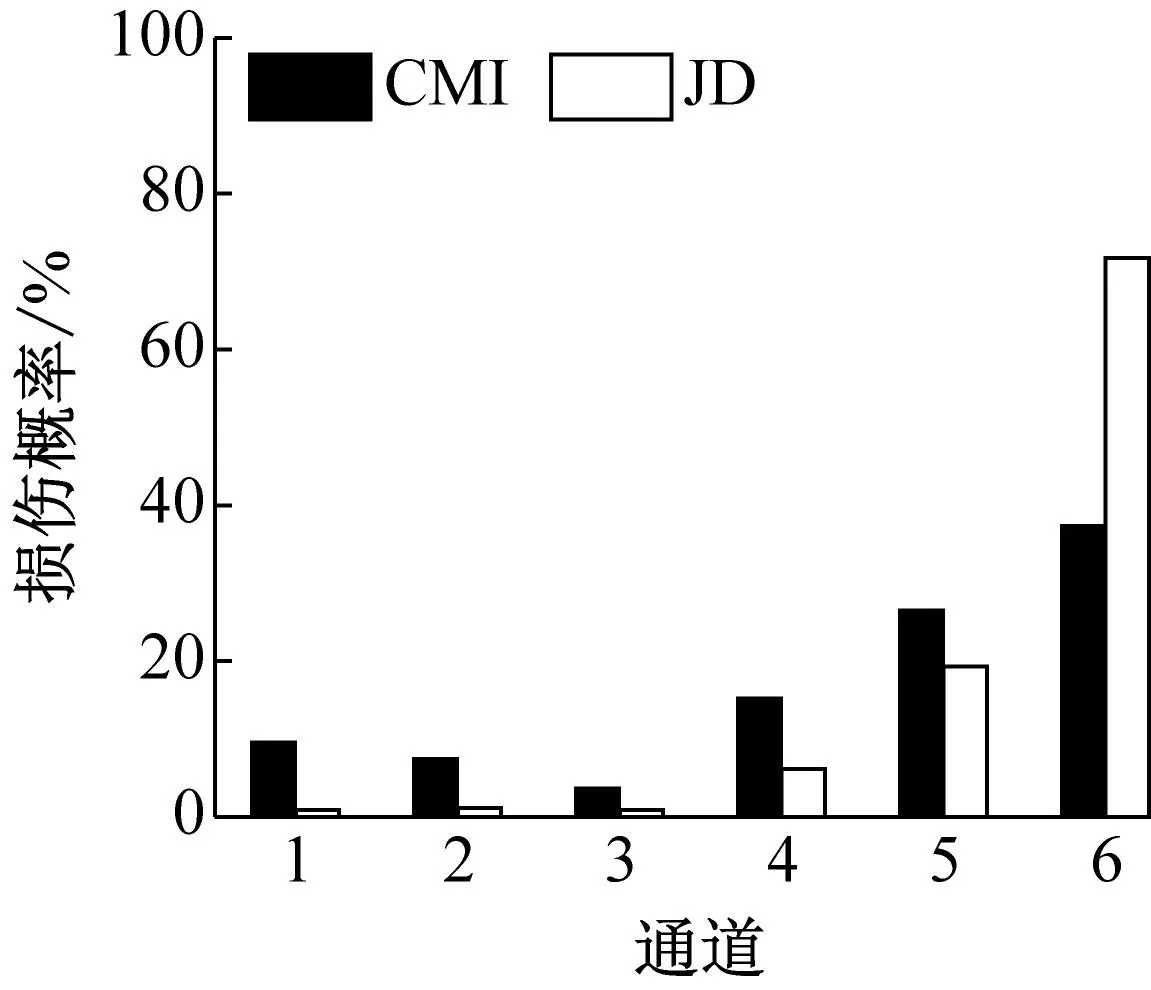
(c) 工况4

(d) 工况5

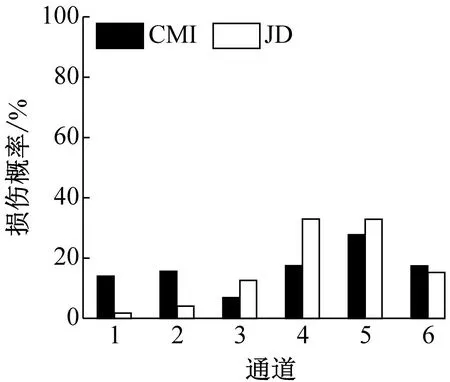
(e) 工况6

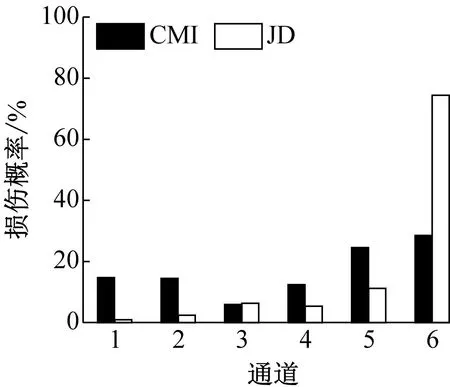
(f) 工况7

图8(a) 显示,由JD指标计算得到的通道1的损伤概率远高于其他通道,表明损伤源最有可能位于第一层;图8(b) 显示,由JD指标计算得到损伤概率表明损伤源最有可能位于通道4和5之间,即损伤最有可能位于第5层;图8(c) 显示,由JD指标计算得到损伤概率表明损伤源最有可能位于通道5和6之间,即损伤最有可能位于第6层,均与实际损伤情况相符。图8(d) ～图8(f) 显示,附加质量对损伤识别结果有一定的影响,但本文提出的方法依然能准确定位结构损伤,表明本文提出的方法受环境变化的影响较小。而应用CMI指标只识别出工况4和工况7中的结构损伤,并且其中未损伤层对应的损伤概率偏高,表明基于ARMA模型和倒谱距离的损伤识别方法对转播塔模型的损伤识别效果较差。

综上,基于ARMAV模型和J-散度距离的结构损伤识别方法能够在所有工况中准确定位损伤,表明该方法能够较好地识别塔式结构的损伤,具有更广泛的应用前景。

5 结 论

本文提出一种基于ARMAV模型和J-散度距离的结构损伤识别方法,采用三层框架结构损伤试验数据加以验证,并开展转播塔模型损伤试验研究,得出以下结论：

(1) 为了提升结构损伤识别的准确性,本文首先采用预白化过滤器对采集到的加速度响应进行了消除激励相关性以及降噪的处理。随后,考虑到即使结构在同一健康状态,激励为同一随机过程,结构输出的信号样本也并不相同,因此将预处理后的数据划分成若干段,建立能够反映不同时序之间相互影响的关系以加强结构损伤特征的多维时序模型ARMAV。

(2) 由ARMAV模型参数和残差方差构造的J-散度距离指标能够准确定位结构损伤,并且其损伤识别结果受环境变化的影响较小。

(3) 在转播塔模型试验研究中,受到转播塔结构层刚度变化及其塔头附加质量等特征的影响,基于ARMA模型的倒谱距离指标难以识别损伤位置,但没有影响本文所提方法对损伤的准确定位,表明本文所提方法受结构体型变化的影响较小,因而该方法的应用前景更广泛。

(4) 该方法在时域中实现,信息获取方便快捷并且无需再次分解,也不用进行频域相关的计算,用其进行损伤识别更高效,为建筑结构损伤的在线实时监测提供一种新思路。

需要指明的是,本文只针对单损伤状态下结构的损伤识别进行研究,后续有待设置多损伤工况,采用ARMAV模型来提取空间损伤特征,以验证本文方法在结构存在多个损伤源情况下的适用性。此外,在采用本文方法准确定位损伤之后,有待进一步对损伤区域内的单元进行损伤类型的判定以及其损伤程度的定量研究。