基于贝叶斯后验估计的桥梁动态称重算法理论与试验研究

张龙威, 原璐琪, 陈 宁, 袁帅华, 张 龙

(1.湖南科技大学 土木工程学院,湖南 湘潭 411201;2.湖南科技大学 结构抗风与振动湖南省重点实验室,湖南 湘潭 411201)

车辆超载现象日渐增加,不仅会降低公路桥梁的使用寿命,还对桥梁的结构安全产生较大危害。桥梁动态称重(bridge weigh-in-motion, BWIM)系统作为新型的车辆称重系统,利用过桥车辆对桥梁的动力响应能快速识别车辆轴质量、轴距、车速等信息[1-3]。它具有安装方便、不中断交通、测试隐蔽、称重精度高且稳定性好等优点,能有效地对行驶在桥面上的车辆进行监控。

目前,传统BWIM系统的核心算法是由Moses[4]在1979年提出的。该算法基于桥梁的理论影响线,利用过桥车辆对桥梁的实测动力响应和理论响应建立误差函数,识别过桥车辆的轴质量。由于Moses算法所采用的理论影响线不能真实地反映桥梁的实际力学特性,OBrien等[5]利用桥梁实测影响线代替理论影响线进行轴质量识别;随后,王宁波等[6]和Zheng等[7]分别利用多项式拟合和最小二乘法QR分解的方法从桥梁的实测动力响应中提取桥梁的实测影响线;张龙威等[8]和Heitner等[9]利用迭代算法分别得到单车过桥时的实测影响线和多车连续过桥时的总体实测影响线。虽然更真实的影响线能够提高车辆轴质量识别的精度,但是,由于桥面可能会出现多车并行的情况,车辆之间对桥梁的响应会相互干扰,影响轴质量识别的准确性。对于这一问题,宫亚峰等[10]利用桥梁的弯矩影响面进行多车共存下的车辆荷载识别;谭承君等[11-12]和邓露等[13]分别引入横向分布系数和神经网络的方法分离多车响应,进行轴质量识别。针对传统BWIM算法仅适用于中小跨径桥梁的问题,邓露等[14]提出虚拟简支梁法,通过隔离桥梁上某一段的应变响应进行轴质量识别,实现大跨度桥梁的动态称重。

上述算法虽然在一定程度上提高了轴质量识别精度,但其核心仍是最小二乘法,忽略了测量误差对轴质量识别的影响。当路面条件较差或者桥梁跨径较大时,轴质量求解方程为病态方程,会出现过拟合,降低轴质量识别精度。为了解决这一问题,Rowley等[15]提出基于正则化的桥梁动态称重算法提高轴质量识别精度;OBrien等[16]运用最大似然估计进行车辆荷载识别。针对传统BWIM算法对于密集群轴难识别的问题,陈适之等[17-18]提出新型桥梁动态称重算法,通过宏应变曲率获取车辆信息,并扩展到二维算法,实现多车并行时的轴质量识别,而且得到了较高的识别精度。虽然这些算法可以改善传统BWIM算法的不足,但计算效率不高且需人工干预。

为解决上述的问题,本文提出一种基于贝叶斯后验估计的桥梁动态称重算法(简称：贝叶斯算法)。该算法利用贝叶斯后验估计,在轴质量求解方程中引入约束因子,用于抑制测量误差对轴质量识别的影响,提高结果精度。通过理论推导得到贝叶斯算法的轴质量计算公式,分别基于数值仿真和实桥试验对比Moses算法和贝叶斯算法轴质量识别结果,验证贝叶斯算法在实际应用中的可行性。

1 动态称重算法

在桥梁动态称重算法中,假定桥梁为一维线弹性的梁,当车辆驶过桥梁时,桥梁的理论荷载响应MTh可通过每个车轴轴质量与其加载位置对应的影响线值乘积求和得到。考虑到误差ε的存在,实测响应Mm表达式为

Mm=MTh+ε=IL·A+ε

(1)

(2)

式中：IL为桥梁影响线矩阵;A为车辆轴质量向量;K和N分别为数据的采样总数和车轴数量。

1.1 Moses算法

传统桥梁动态称重系统是以Moses算法作为核心算法进行轴质量识别。首先,基于最小二乘法,根据桥梁的实测响应Mm和理论响应MTh建立误差函数E,即：

(3)

然后,令误差函数E对每个车轴求偏导。最后,当偏导值等于零时,误差函数E取最小值,所对应的结果即为桥梁上行驶车辆的轴质量,具体求解过程见文献[19]。车辆轴质量A的表达式为

A=(ILTIL)-1ILTMm

(4)

式中,影响线IL由影响线算法得到影响线向量变化而成。

1.2 贝叶斯算法

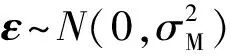
由贝叶斯定理[20]可知,车辆轴质量A的后验概率与实测响应Mm似然估计P(Mm|A)和车辆轴质量A的先验概率P(A)的乘积成正比,即：

P(A|Mm)∝P(A)P(Mm|A)

(5)

(6)

(7)

当后验概率P(A|Mm)取最大值时,所对应的轴质量A的计算公式为

(8)

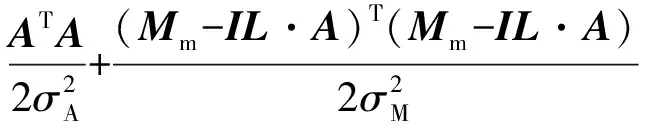
(9)

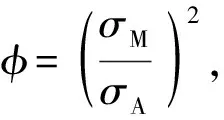
E=min[(Mm-IL·A)2+φATA]

(10)

轴质量表达式的求解过程同Moses算法相似,具体可参考文献[21]。最终得到车辆轴质量A的表达式

A=(ILTIL+φI)-1ILTMm

(11)

式中：I为单位矩阵;φ为约束因子,由桥梁响应测量误差的标准差σM和轴质量的标准差σA确定。其中：σM通过桥梁实测响应和理论响应的差值得到;σA利用贝叶斯线性回归的方法确定。

由于车辆轴质量A的先验概率和实测响应Mm的似然估计均服从共轭高斯分布,根据贝叶斯定律,车辆轴质量A的后验概率同样服从高斯分布,即：

(12)

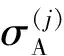
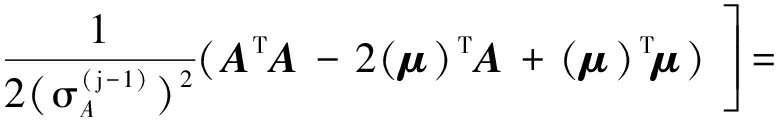
(13)

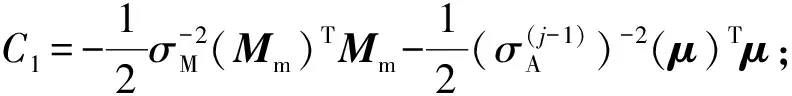
另一方面,根据概率分布,车辆轴质量A的后验概率可以写成

(14)

通过对比式(13)和式(14)中的二次项,可以得到

(15)

在求解过程中,对轴质量的标准差赋予初值,通过式(15)反复迭代出轴质量的标准差。测量误差的标准差先通过桥梁响应的实测值和第i次轴质量迭代得到的轴质量所计算的响应理论值求差得到测量误差,计算公式为Mm-IL·A(i),进而计算出相应的标准差。这里需要指出的是,轴质量初值A(0)的选择与轴质量初始分布无关。

基于贝叶斯后验估计的桥梁动态称重算法的详细计算过程如图1所示。

步骤1获取初始轴质量A(0)。假定初始的约束因子φ(0)=0,利用轴质量方程A=(ILTIL+φI)-1ILTMm得到初始轴质量A(0)。

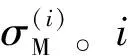
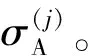
步骤5确定车辆轴质量A。重复步骤2～步骤4,直至车辆轴质量收敛且相邻两次迭代的轴质量差值的绝对值小于阈值e2为止,即：e2>|A(i)-A(i-1)|。最后迭代步i所对应的轴质量A(i)作为车辆轴质量A的最终结果。

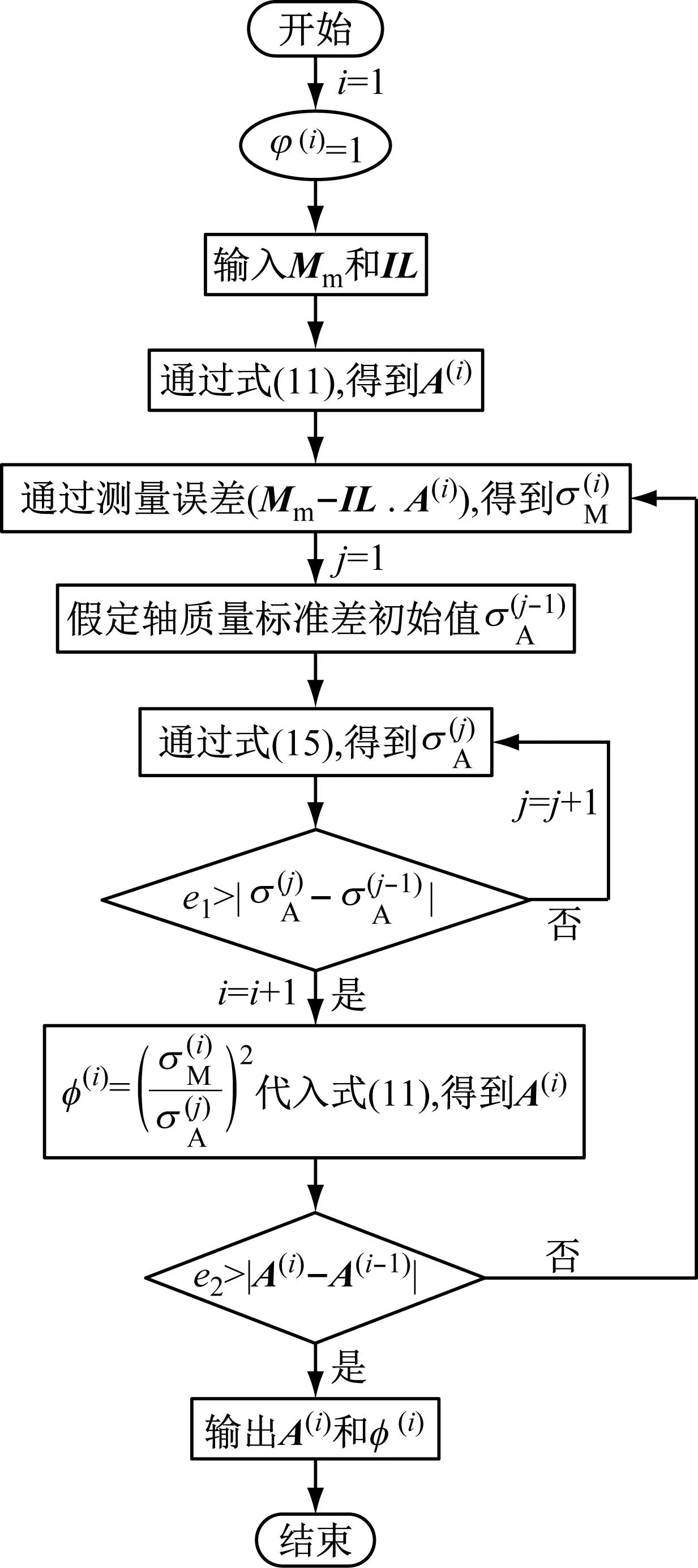
图1 贝叶斯算法流程图

2 数值仿真

为了验证贝叶斯算法的可行性和准确性,本文基于车-简支梁耦合动力数值模型,进行相关研究。

2.1 车桥耦合数值模型

本文采用数值模型模拟随机车流以不同的速度沿简支梁桥中心线匀速驶过,如图2所示。桥梁模型为欧拉-伯努利简支梁,跨径L=10 m、弹性模量E=3.5×1010N/m2、截面惯量Jb=0.132 m4、线密度μ=4 278 kg/m、阻尼比ζ=3%。车辆模型为两轴车,由线弹性体、质量元件和刚度元件构成。车辆参数根据实测数据得到,车辆的每个参数都服从高斯正态分布,通过蒙特卡洛随机生成100辆车驶过桥梁,具体数值如表1所示。其中,每辆车的速度服从均值为80 km/h、标准差为8 km/h的正态分布。路面粗糙度等级选用A级和C级,分别模拟路面完好和路面变差时的工况。车桥耦合求解方法为Newmark-β法,时间步长为1×10-4s。为了模拟实际情况下的噪声信号,加入2%的高斯噪声,得到的桥梁跨中梁底的应变响应,共200组(100辆车×2种粗糙度),用于轴质量识别。图3为同一辆车分别在A级和C级路面下的动力应变响应。图4为用于称重的桥梁跨中位置梁底的理论影响线。考虑到车辆上桥段和出桥段所引起的桥梁动力响应对轴质量识别结果的影响,桥梁影响线长度定为20 m,即5 m(上桥段)+10 m(桥长)+5 m(出桥段)=20 m。

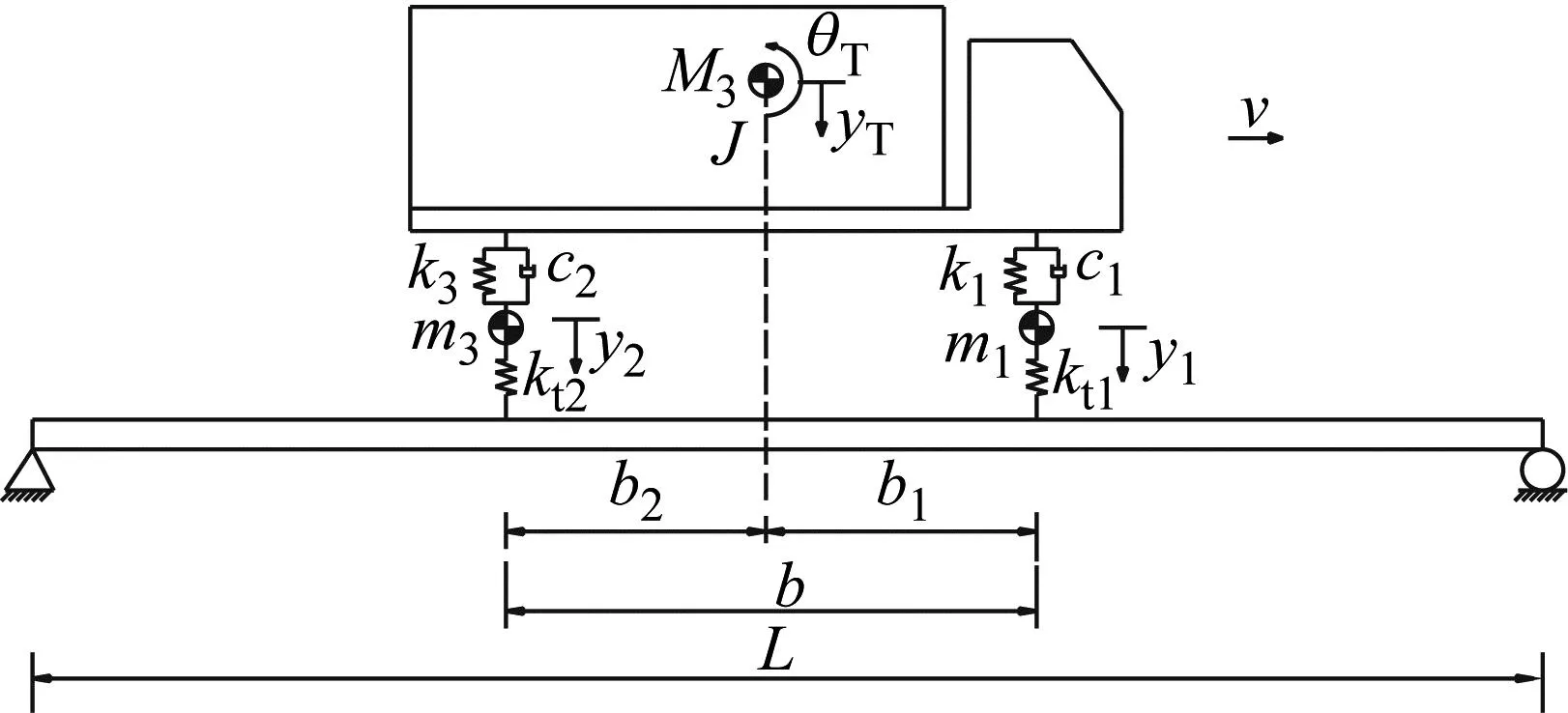
图2 车桥模型示意图

表1 车辆参数

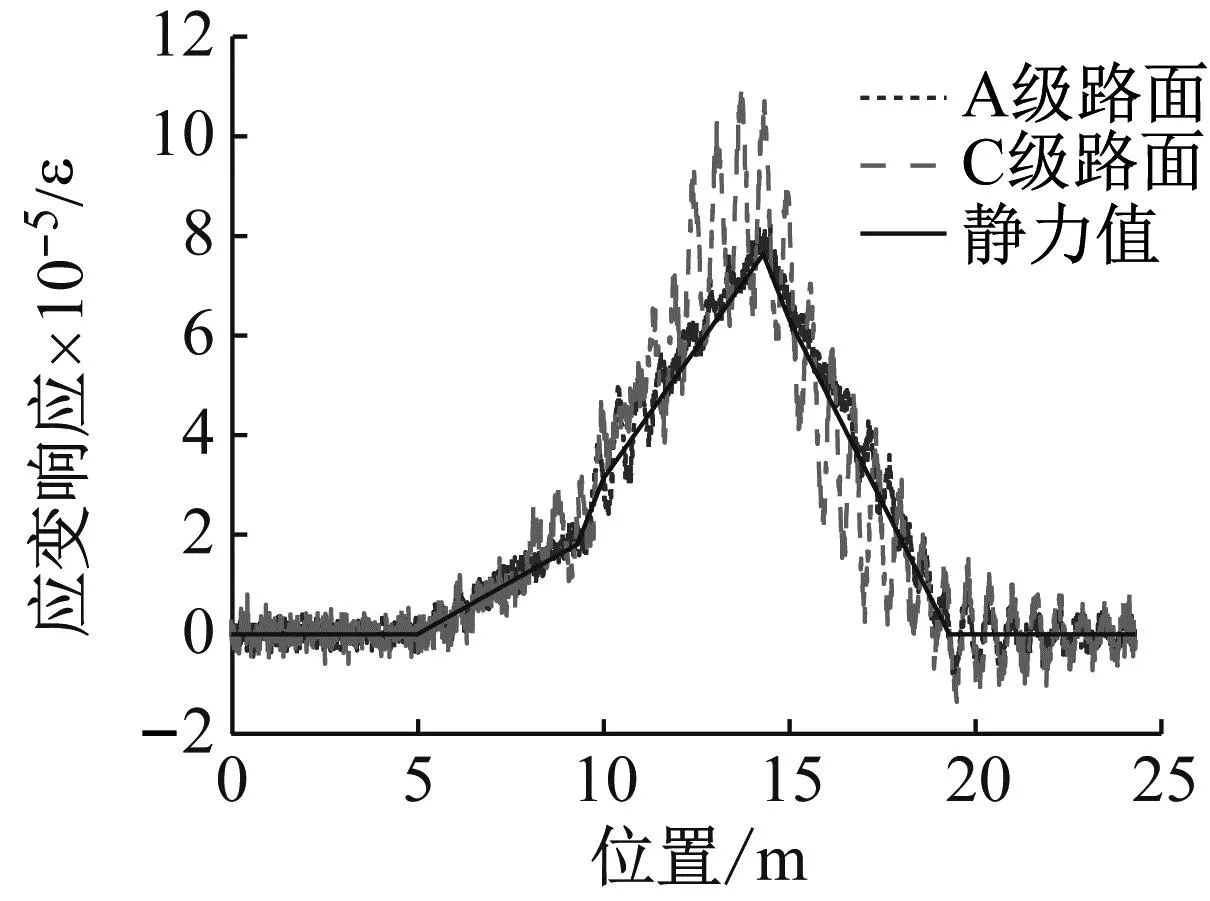
图3 桥梁跨中位置处应变响应对比图

2.2 结果分析

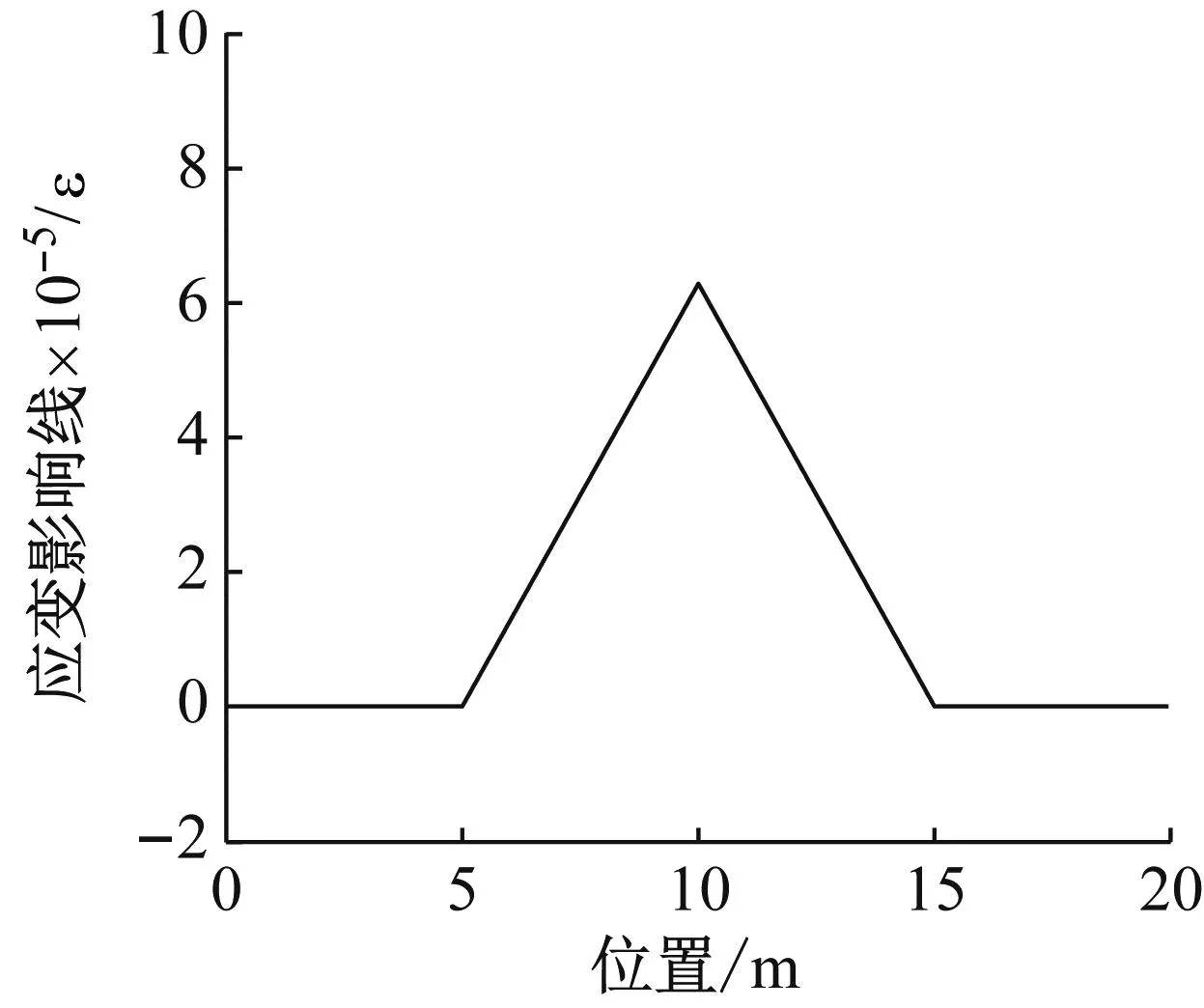
图4 桥梁跨中位置处理论影响线

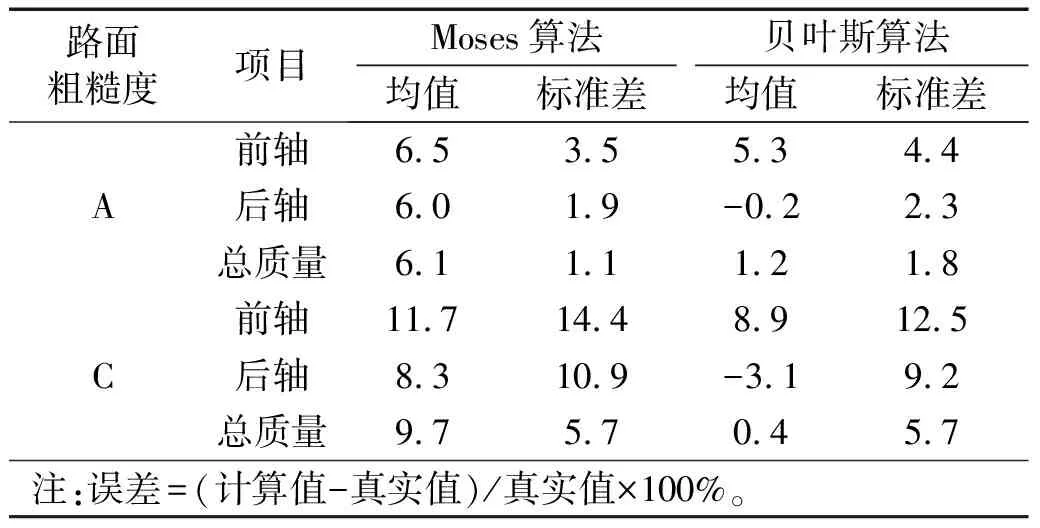
表2 两种算法轴质量识别结果误差表

从表2可以看出：

(1) 当路面粗糙度为A级时：①两种算法轴质量识别误差的标准差相差不大,但贝叶斯算法得到的轴质量误差均值低于Moses算法,特别是后轴和总质量,例如,贝叶斯算法的后轴轴质量误差均值为-0.2%,远小于Moses算法的后轴轴质量误差均值6.0%。这表明,贝叶斯算法能在一定程度上提高轴质量识别的精度。②贝叶斯算法对后轴和总质量的识别精度要明显高于前轴轴质量的识别精度,例如,贝叶斯算法的前轴轴质量误差均值(5.3%)明显高于后轴轴质量误差均值(-0.2%)和总质量误差均值(1.2%),而且前轴的稳定性也要比后轴和总质量的稳定性差。出现这一现象主要是因为,贝叶斯算法对轴质量数值较大的车轴识别精度高,以总质量识别结果为例,其误差均值趋于0(1.2%)。这也意味着前轴和后轴轴质量误差绝对值的数值相近、符号相反。

(2) 当路面粗糙度为C级时：①贝叶斯算法的轴质量识别结果明显优于Moses算法,以前轴为例,贝叶斯算法的误差均值(8.9%)和标准差(12.5%)均小于Moses算法相应的结果(均值：11.7%,标准差：14.4%);②贝叶斯算法的总质量识别精度明显高于单轴的识别精度;③Moses算法的单轴轴质量和总质量误差的均值相近,但总质量误差的标准差(5.7%)明显低于单轴误差的标准差(前轴：14.4%,后轴：10.9%)。

(3) 对比不同粗糙度下两种算法的轴质量识别结果,可以看出：①随着路面条件变差,两种算法的轴质量识别精度均会明显降低,以贝叶斯算法为例,前轴误差均值由5.3%(A级)增加到8.9%(C级),标准差由4.4%(A级)增加到12.5%(C级);②路面越不平整,贝叶斯算法对Moses算法轴质量识别精度的提升越明显。例如,A级路面时前轴的误差均值由Moses算法的6.5%降至贝叶斯算法的5.3%,误差减小了1.2%。随着路面变差,相比于Moses算法,贝叶斯算法在C级路面时前轴的误差降幅达到了2.8%。

综上所述,贝叶斯算法可以在一定程度上提高轴质量识别精度,而且路面条件越差,精度提升得越明显。

为了深入探究贝叶斯算法在桥梁动态称重系统中优于Moses算法的原因,现选取同一辆车在不同粗糙度下的动力响应(图3)进行阐述。

从图3可以看出,随着路面粗糙度的增加,车辆驶过桥梁时的动力响应出现不同幅度的波动,即：当路面条件较好时(A级),车辆对桥梁的动力响应在静力值附近上下波动;当路面条件变差时(C级),其动力响应波动幅度变大,且数值普遍高于所对应的静力值。在进行轴质量识别时,所采用的影响线是桥梁跨中位置梁底的理论影响线(如图4),始终保持不变。随着路面粗糙度增大,实测桥梁动力响应的测量误差随之增加。由于Moses算法未考虑测量误差的影响,当测量误差增大时,轴质量识别的精度就会降低。相比之下,贝叶斯算法考虑了测量误差和车辆轴质量的波动,假设测量误差和轴质量服从高斯分布,利用测量误差的标准差和轴质量标准差得到约束因子,用于抑制测量误差对轴质量识别的影响,从而提高桥梁动态称重的精度。

此外,图5和图6分别绘制出轴质量误差标准差和约束因子在迭代计算过程中的变化过程。

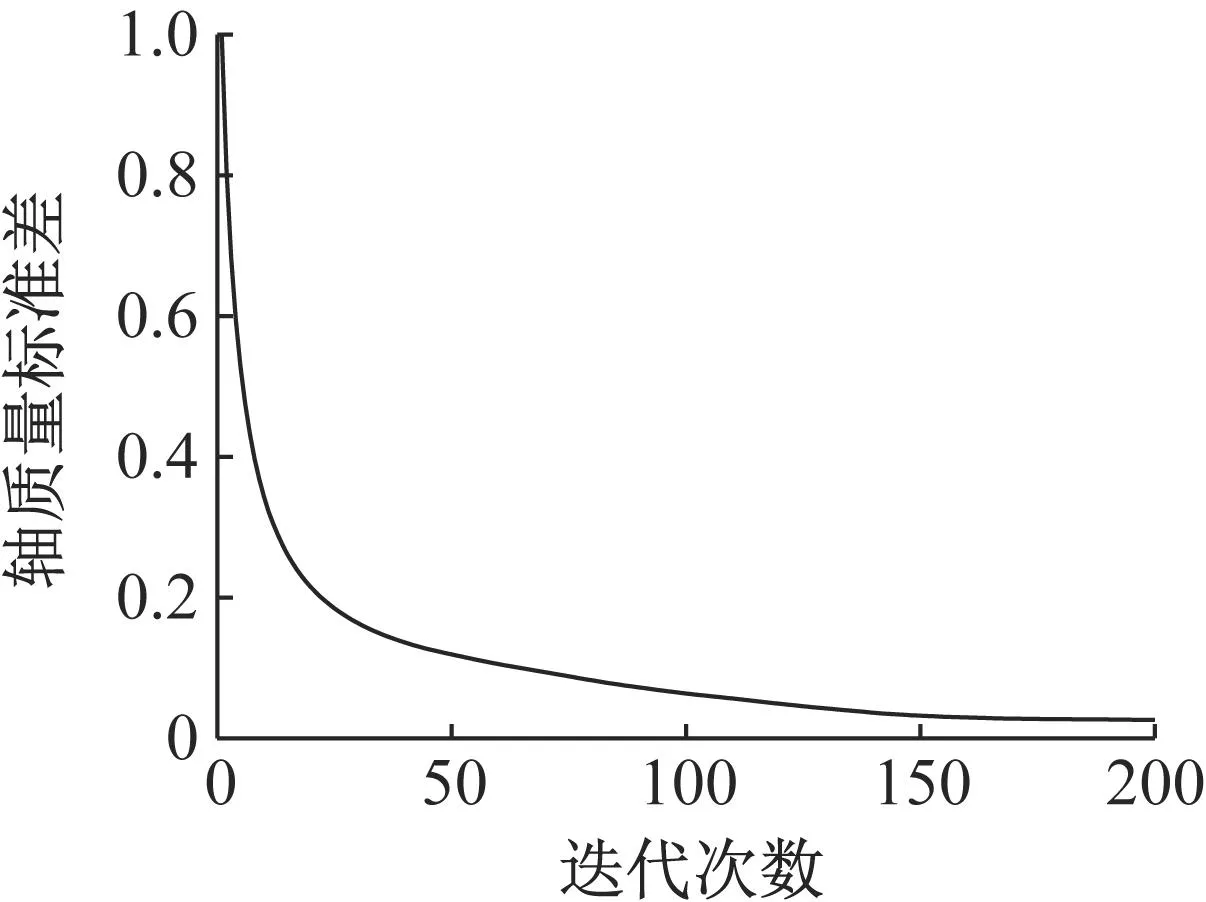
图5 轴质量标准差迭代变化曲线

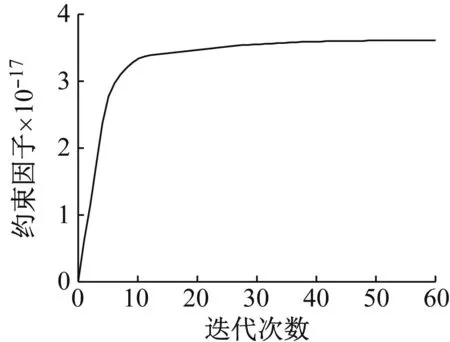
图6 约束因子迭代变化曲线

由图5和图6可知,在计算过程中,即使初值与最终结果有较大偏差,也能迅速收敛,得到稳定结果。综上所述,贝叶斯算法能够在较高的计算效率下,抑制测量误差对轴质量识别的影响,从而提高桥梁动态称重的精度。

3 实桥试验

为了验证贝叶斯算法在实测桥梁中的适用性,本文将湖南省怀化市舞水五桥引桥作为研究对象,进行相关研究。

3.1 试验概况

怀化市舞水五桥引桥是由10片T梁组成的简支梁桥,跨径40 m,桥宽24 m,桥面布置为：4×3.5 m(行车道)+2×3.0 m(非机动车道)+2×2.0 m(人行道)=24 m,主梁横断面示意图如图7所示。具体参数见文献[22]。

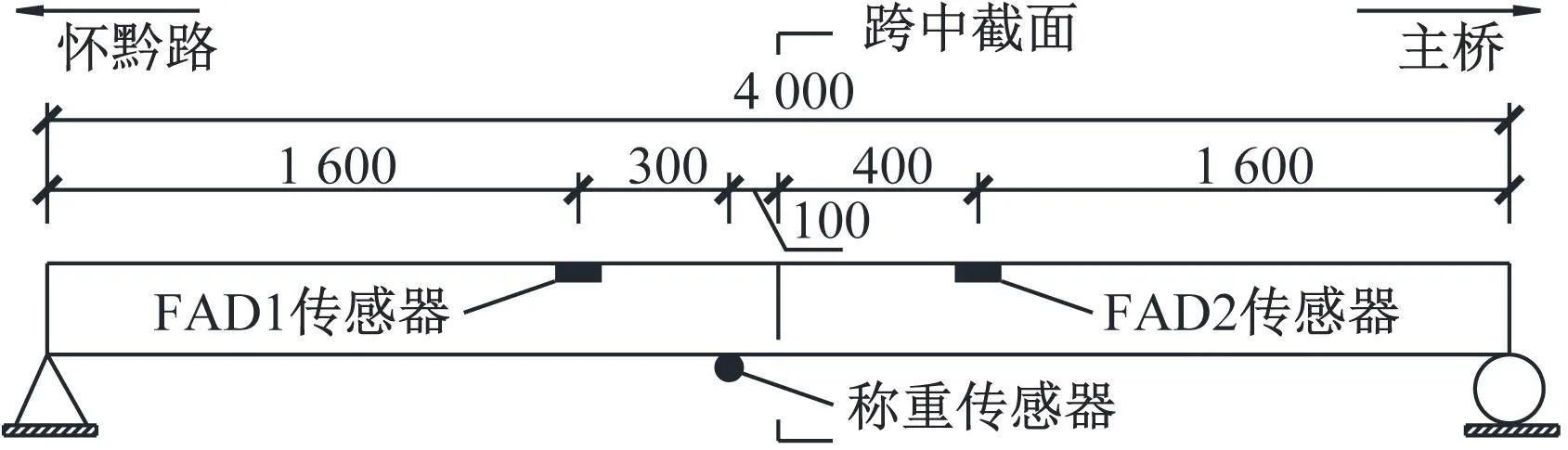
(a) 立面图

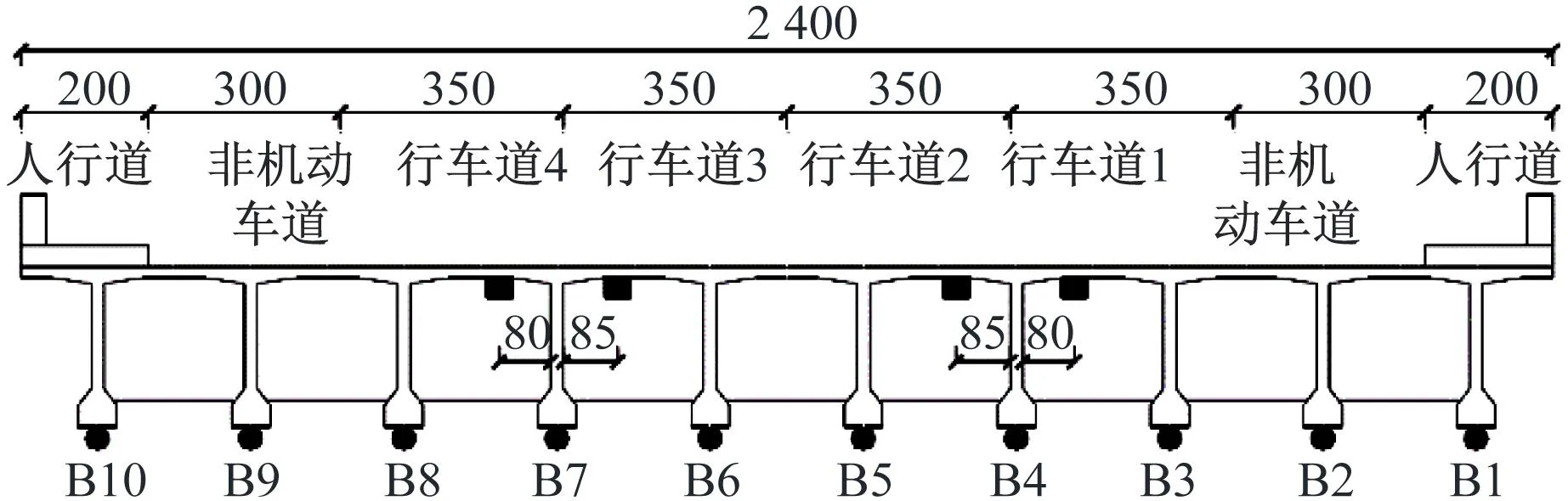
(b) 横断面图

试验选用一辆两轴车作为加载车辆,按照30 km/h匀速沿着车道中心线反复从桥梁的第三车道驶过,共10趟。加载车辆前轴轴质量7.4 t,后轴21.1 t,总质量28.5 t,轴间距4.7 m。在试验过程中,通过安装在桥梁跨中截面两侧翼缘板下的车轴探测传感器(free-of-axle-detector,FAD)获得车辆信息(车辆轴间距、车轴数、车辆速度等);利用安装在跨中位置T梁底部的称重传感器(B1～B10)获取车辆驶过桥梁时的动态应变响应,用于轴质量识别。其中,为了使FAD传感器得到的信号峰值位置更加明显,分别用小波变换的方法对FAD传感器测得的响应进行处理[23]。传感器具体的安装位置见图7。试验采用扬州科动KD4001工具式应变传感器和日本TML公司的DC-204动态应变采集仪。测量信号采集频率200 Hz。现场试验系统布置如图8所示。

3.2 结果分析

本文分别利用贝叶斯算法和Moses算法对实测的车桥动力响应进行轴质量识别,计算结果如表3所示。其中,用于轴质量识别的车桥实测动力响应是10个称重传感器(B1～B10)所测得的动力响应之和,见图8(c)。影响线通过实测影响线算法从桥梁的实测影响中提取而来(图9)。

(a) 加载车

(b) 数据采集仪

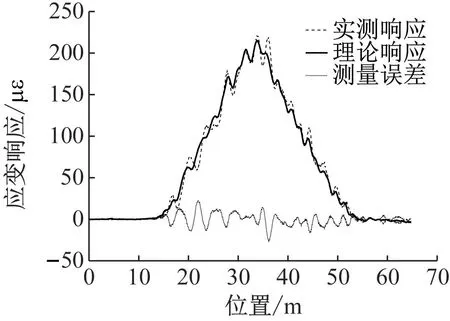
(c) 车桥动力应变响应

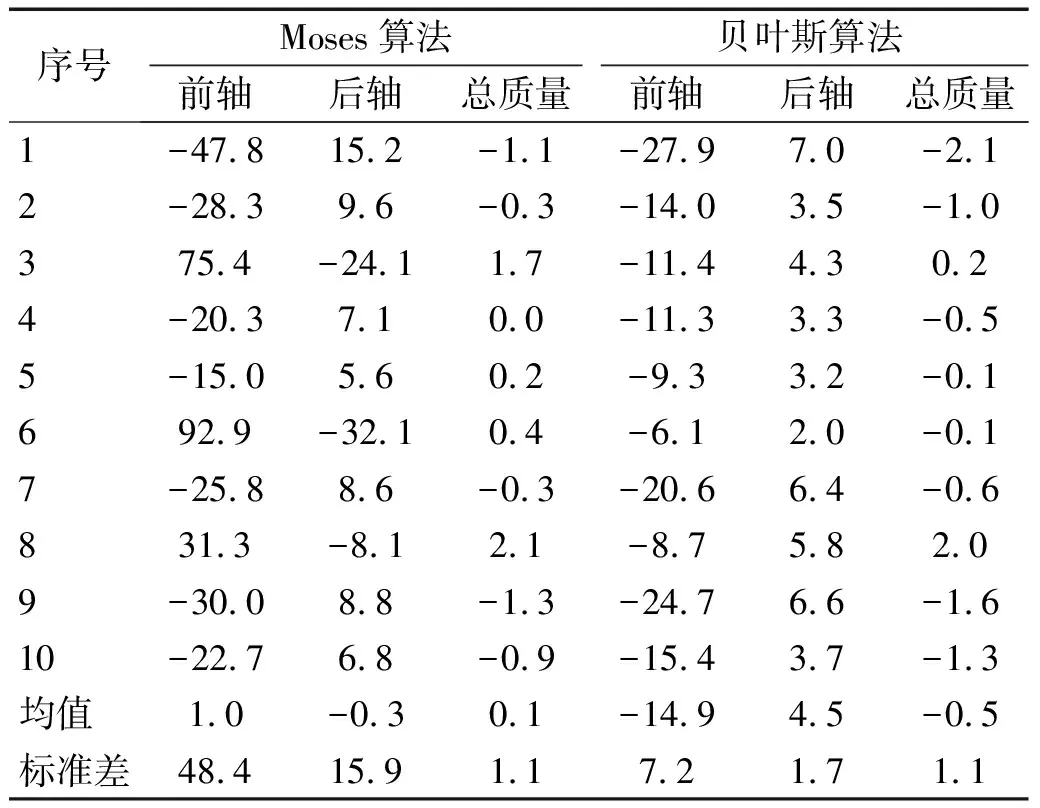
表3 两种算法轴质量识别结果误差表

由表3可知：①Moses算法能较准确地得到车辆总质量,均值误差为0.1%,标准差为1.1%。然而,单轴误差偏大,且稳定性差。前轴的最大误差达到了92.9%,标准差为48.4%。这表明Moses算法对跨径较大的桥梁进行轴质量识别,无法得到准确的单轴轴质量。②不同于Moses算法,贝叶斯算法不仅能够得到较高精度的车轴总质量,还能较准确地识别单轴轴质量。对于每一组实测数据,贝叶斯算法的单轴轴质量误差绝对值都远低于Moses算法的结果。以第一组数据为例,贝叶斯算法的前轴误差为-27.9%,远好于Moses算法的结果(-47.8%)。③两种算法对于总质量的识别精度明显优于单轴的识别精度。比如,对于第5组数据,贝叶斯算法的总质量计算误差为-0.1%要明显低于单轴的识别精度(前轴：-9.3%,后轴：3.2%)。

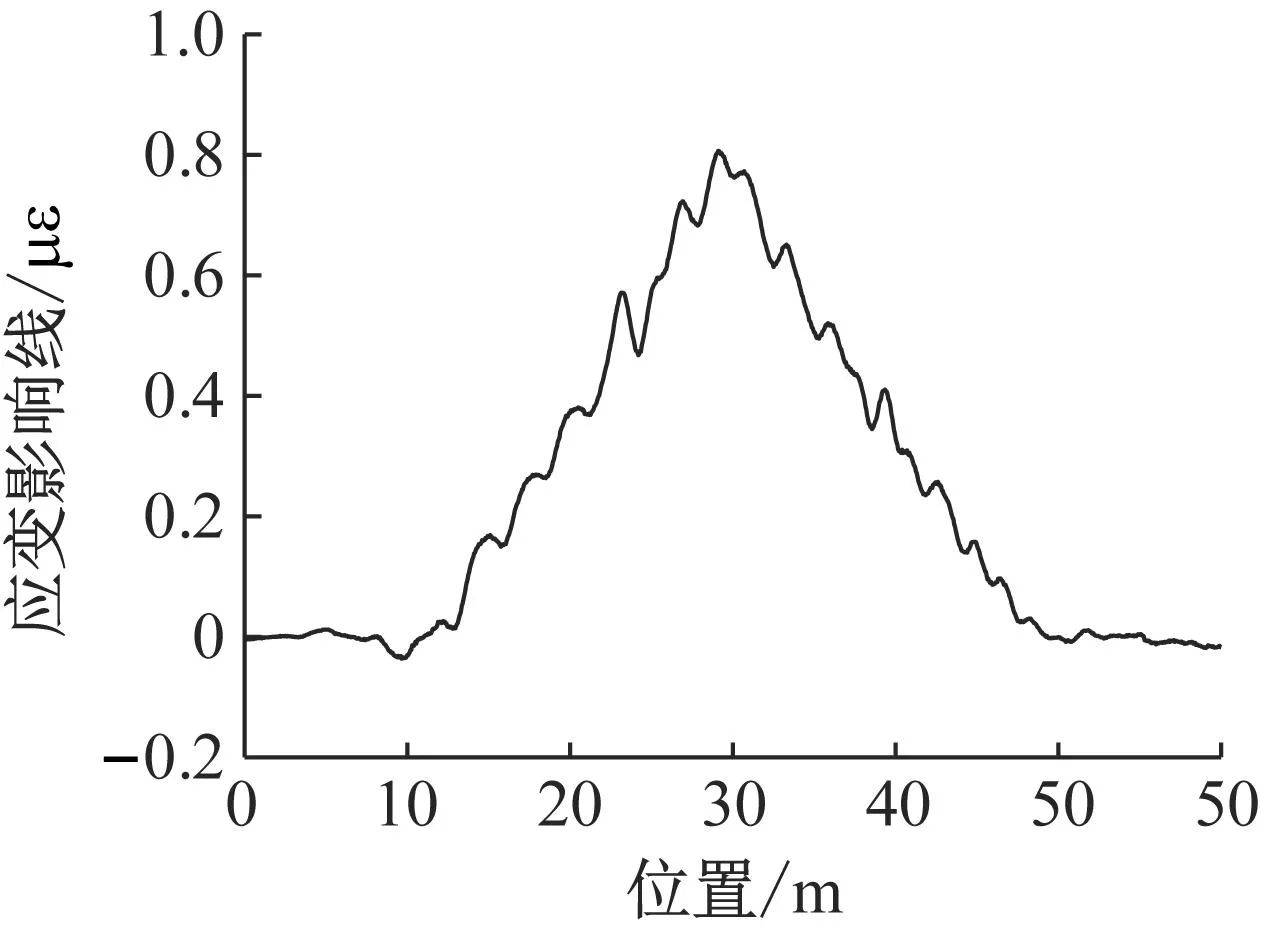
图9 实测均值影响线

为了进一步说明贝叶斯算法提高轴质量识别精度的原因,现选定第7组数据(图8(c))进行分析说明。

从图8(c)可以看出,实测应变响应的车桥耦合效应明显,曲线频繁上下波动,从而导致实测的测量误差曲线上下波动频繁,测量误差偏大。结合上文可知,测量误差越大,相对应的Moses算法的轴质量识别精度就越差。对于贝叶斯算法,在轴质量识别过程中考虑了测量误差和轴质量的波动,参照图1,计算出实测响应所对应的测量误差标准差和轴质量误差标准差,进而得到约束因子,用以抑制测量误差对轴质量识别的影响。此外,从约束因子的迭代曲线(图10)可看出,对于实测响应,约束因子只需要经过20次左右的迭代就能收敛,有较高的计算效率。总的说来,贝叶斯算法不仅计算效率高,而且能在一定程度上提高Moses算法的轴质量识别精度。

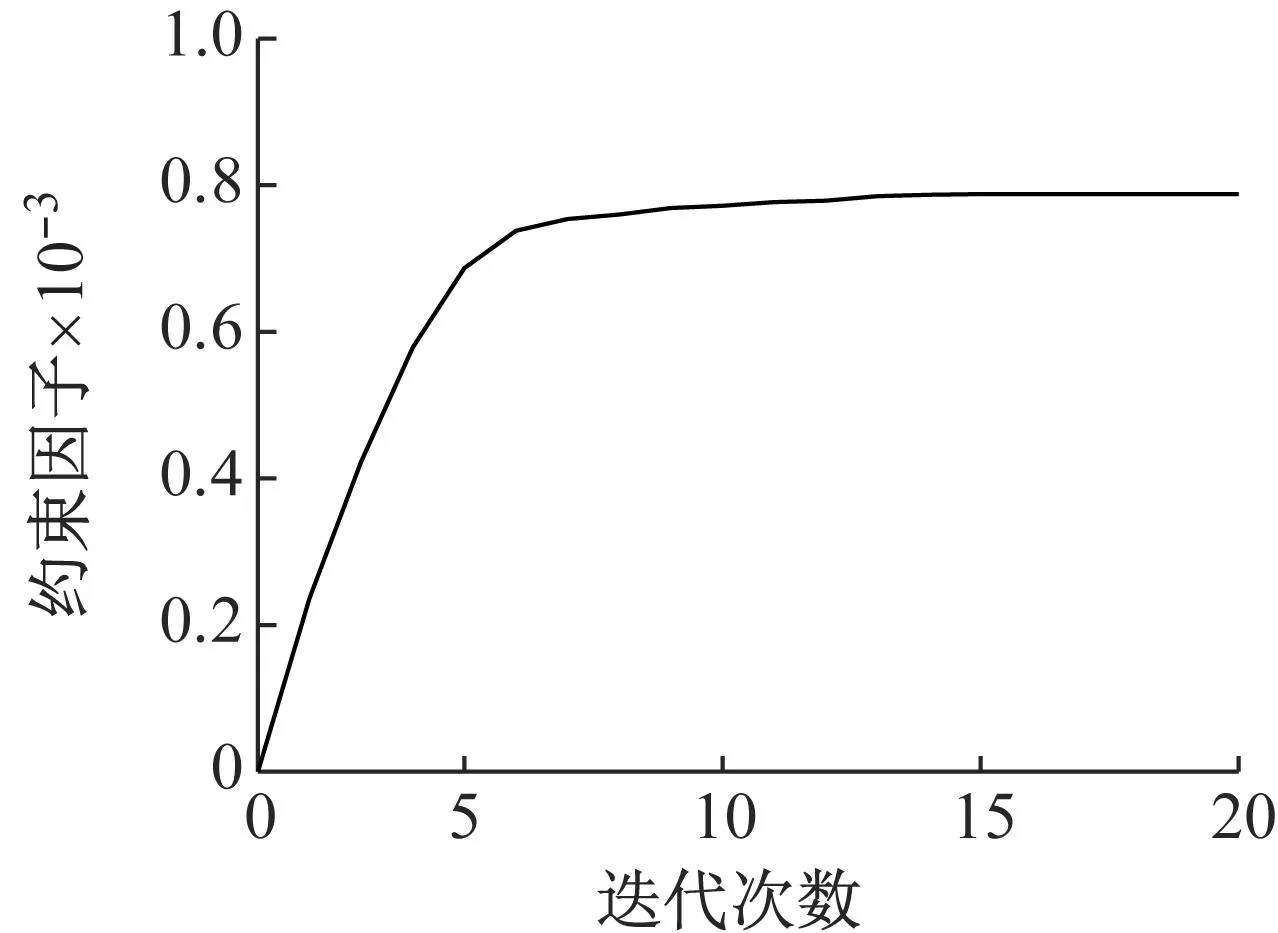
图10 约束因子迭代曲线

4 结 论

为了提高桥梁动态称重系统的轴质量识别精度,本文提出一种基于贝叶斯后验估计的桥梁动态称重算法。该算法考虑了测量误差对轴质量识别精度的影响,假设测量误差和轴质量均服从高斯分布,利用测量误差的标准差和轴质量标准差得到能抑制测量误差的约束因子,用以提高轴质量识别精度。基于车桥数值仿真和实桥动力试验,对比了贝叶斯算法和Moses算法轴质量识别结果,得到如下结论：

(1) 通过车桥数值仿真模型试验所得到的轴质量识别结果可以看出,同种工况下,贝叶斯算法的单轴和总质量精度都高于Moses算法。

(2) 随着路面粗糙度的增加,两种算法的轴质量识别精度都会有所降低,但贝叶斯算法相较于Moses算法的降幅不明显。这表明贝叶斯算法消除了一部分测量误差对轴质量识别的影响。

(3) 由实桥试验的结果可知：相比于Moses算法,贝叶斯算法能够大幅度地提高单轴的识别精度。其中,前轴的误差标准差从Moses算法的48.4%降至贝叶斯算法的7.2%。

(4) 两种算法对总质量的识别精度要高于单轴识别精度,而且对于单轴来说,车轴轴质量越大,相应的轴质量识别精度越高。