振动标线设置对连续梁桥的挠度冲击系数影响研究

张 恒, 周勇军,2, 王业路, 范凯翔, 赵 煜,2, 薛宇欣

(1.长安大学 公路学院,西安 710064;2.长安大学 公路大型结构安全教育部工程研究中心,西安 710064)

随着我国公路交通事业的飞速发展,高速公路向山区延伸。长大坡桥作为山区公路常见结构,往往是车辆超速失控的主要路段。为了能够控制车速,减少交通事故的发生,设置减速振动标线是一种行之有效的重要措施。减速振动标线主要是针对雨天行车情况下可视程度较低而提出的一种新型标线,它利用凹凸的结构形式达到强制减速和提示驾驶员减速的效果,起源于日本。最初开展的减速振动标线研究是在道路领域。徐翔等[1]认为设计振动标线时必须综合考虑车辆、路面和环境等多重因素;袁振友等[2]通过对一级公路交叉口交通事故的原因进行分析,表明利用减速振动标线等措施可减小事故发生率并减轻事故危害;候树展等[3]研究了车辆通过3类振动减速标线的速度变化特征;余金林等[4-5]研究了振动标线对舒适度的影响,分析了不同减速效果下驾驶员的舒适性,研究发现参数优化后的振动减速标线明显改善限速效果并提高了驾乘人员的行车舒适性。

减速振动标线因其凹凸特性实质上是一种桥面不平顺度,也会引起车辆对桥梁结构的冲击效应。相关学者关于桥面不平顺对桥梁结构动力特性的影响开展了大量研究：Calcada等[6]研究发现桥面不平顺度是桥梁冲击效应的最主要影响因素;Chatterjee等[7]根据10个桥面不平顺样本,计算了冲击系数的均值和偏差;Michaltsos[8]研究发现了桥面不平顺度激励作用位置的重要性;Li等[9]认为桥面不平顺的峰值位置对冲击系数有很大影响;卜建清等[10]考虑了桥面不平顺度、桥梁结构损伤情况及车速等因素,研究其对车桥耦合振动的影响规律;薛宇欣等[11]基于手机加速度采集客户端构建空间桥面不平顺度模型,依据自编MATLAB程序研究空间桥面不平顺度对桥梁冲击系数的影响;蒋培文等[12]基于ANSYS二次开发APDL语言编制了车桥耦合软件,考虑桥面不平顺,研究了单辆、多辆空间车辆模型以匀速、匀变速通过桥梁的车桥耦合振动响应;刘晨光等[13]针对桥面不平顺对桥梁冲击系数的影响机理、不平顺度等级与冲击系数之间关系以及冲击系数的检测方法等问题,提出了一种可预判桥面退化后冲击系数是否符合要求的新型检测方法。

综上所述,虽然诸多专家学者对减速振动标线和桥面不平顺等问题开展了大量研究,也取得了丰硕成果,但减速带作为一个规则的“桥面不平顺”与随机的桥面不平顺度有一定区别,桥梁设置振动标线时借用道路的研究成果,未曾考虑其对桥梁结构振动冲击的影响。本文利用有限元分析软件,分别建立连续梁桥、车辆和振动标线模型,分析不同工况下桥梁结构跨中位置的挠度时程曲线,研究振动标线的设置对于桥梁冲击系数的影响,并对振动标线的合理设置提出建议。

1 车桥耦合动力响应分析方法

1.1 车桥耦合动力响应分析理论

基于接触点处接触力与位移的耦合关系,联立桥梁与车辆各自的振动方程,可得到车辆-桥梁体系的动力方程如式(1)[14]

(1)

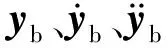
1.2 有限元分析方法及验证

利用有限元程序ANSYS的瞬态分析功能,通过APDL语言分别建立车辆和桥梁模型,采用Mass21单元模拟车体、转向悬挂以及车轮质量;Beam3单元模拟主梁、车体和悬架;Combin14模拟弹簧的刚度及阻尼。采用位移接触法建立车桥耦合振动方程,并采用直接积分法求解该时变方程。为验证本文程序的正确性,选取文献[15]中的桥梁与车辆参数,分别计算车辆以40、60、120、160、200 km/h通过该桥时的跨中挠度如图1(a)所示,与文献结果进行对比如图1(b)所示。分析可知,两者计算结果吻合度较高,说明可采用该程序进行本文的有限元模拟分析。

2 车辆-桥梁-振动标线模型

2.1 桥梁模型

根据JTG D60—2015《公路桥涵设计通用规范》规定,桥上纵坡不宜大于4%。在此坡度范围内,桥上纵坡对连续梁桥频率影响较小[16],为简化分析,这里不考虑纵坡的影响。选取2×30 m、3×30 m及4×30 m连续小箱梁为研究对象,材料为C50混凝土,截面形式和车辆加载位置如图2所示,采用2#梁动挠度时程曲线进行分析。基于ANSYS建立连续梁桥空间梁格有限元模型,主梁、横梁采用Beam188单元模拟,桥面采用Shell63单元。典型连续梁桥有限元模型如图3所示。

2.2 车辆模型

本文选用1/2五轴车辆模型进行分析,其计算模型如图4所示,参数如表1所示[17]。

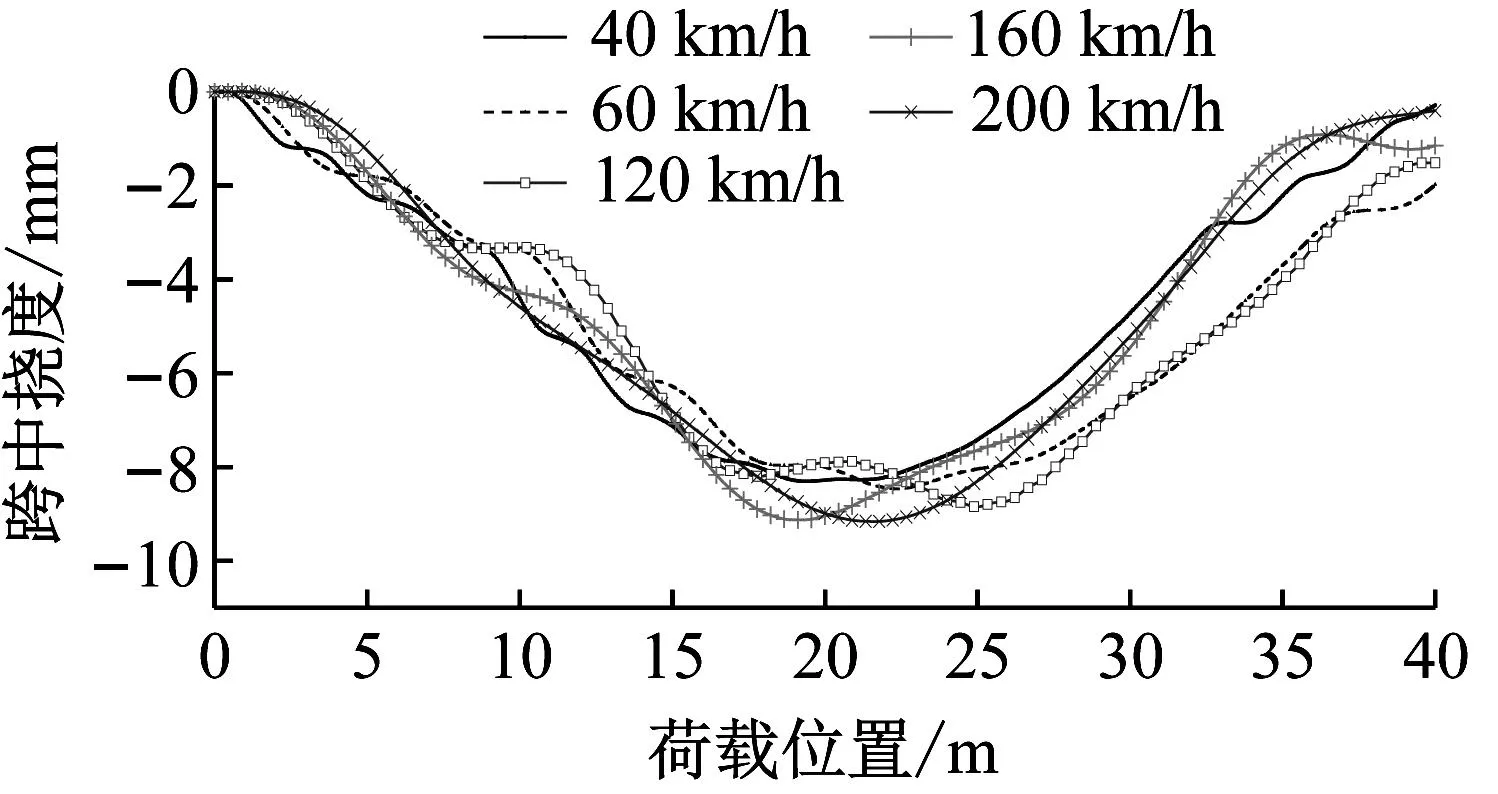
(a) 本文程序

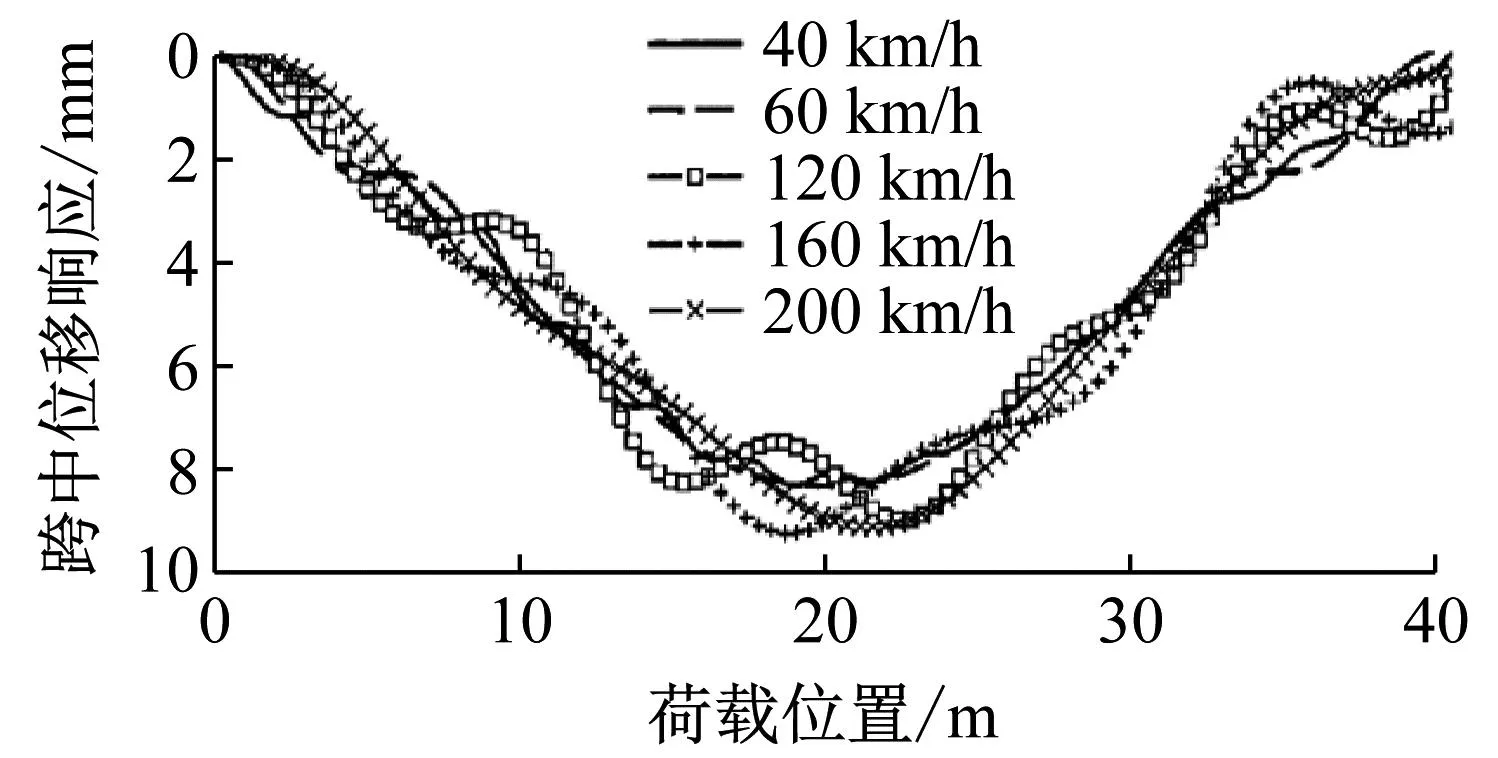
(b) 参考文献[15]

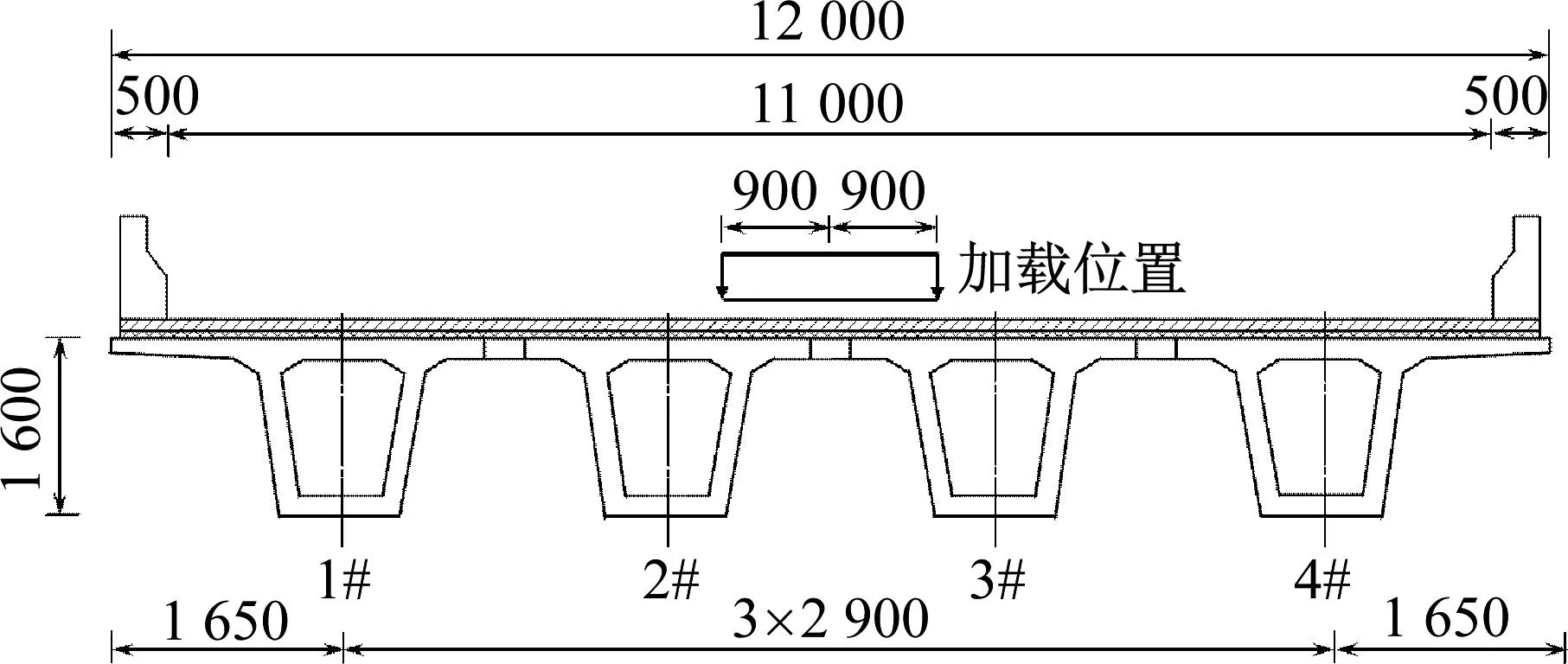
图2 桥梁横截面和车辆加载位置(mm)

图3 2×30 m跨径连续梁桥有限元模型

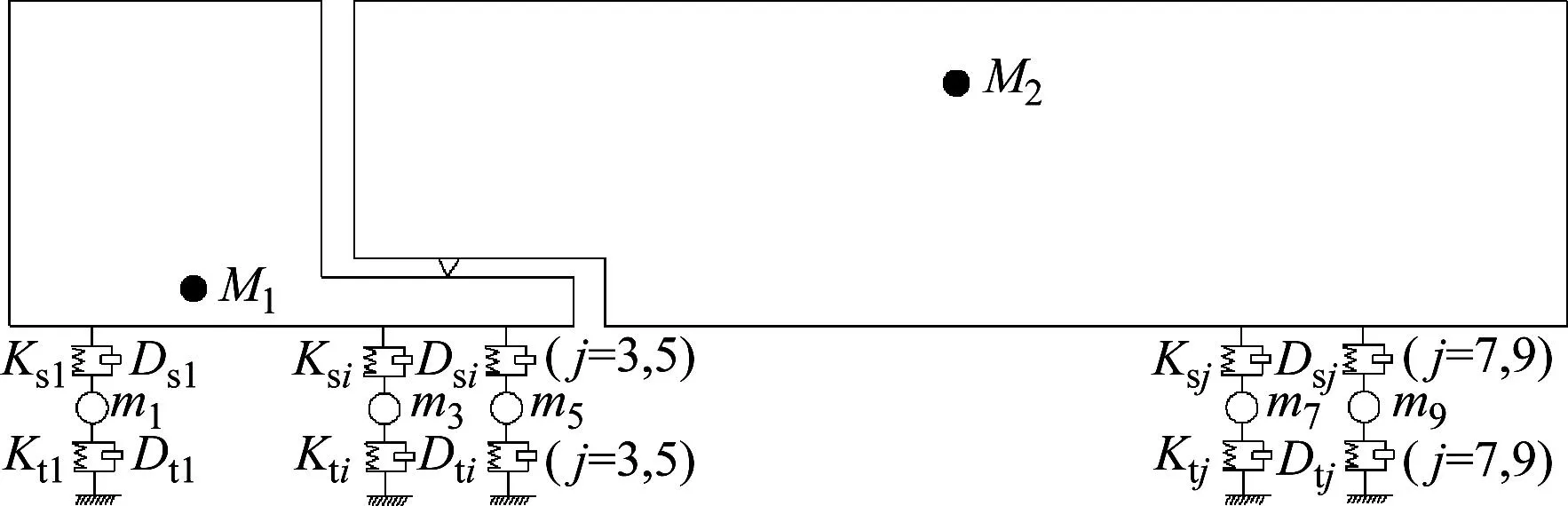
图4 1/2车辆模型

表1 车辆模型的参数取值

2.3 振动标线模型

本文按照JTG D82—2009《公路交通标志和标线设置规范》规定,研究减速带振动标线组数(N)、组间距(d)及首条振动标线距梁端距离(D)对桥梁结构振动响应的影响。振动标线示意如图5(a)所示。振动标线凸起厚度在5～7 mm。本文拟定为7 mm,基底厚度拟定为2 mm。图5(b)为实际路段中振动标线布置。其中,振动标线间的桥面为A级路面,因此桥面不平顺度采用A级桥面不平顺等级并在其基础上叠加振动标线模型进行模拟。

桥面不平顺度在实际中通常用功率谱来描述其统计特性,可拟合为

(2)

式中：n为空间频率;n0为参考空间频率;Gx(n)是位移功率谱密度值;Gx(n0)是路面不平顺度系数;ω为频率指数,通常ω=2。

根据GB/T 7031—2005《机械振动道路路面谱测量数据报告》,本文采用三角级数叠加法模拟。

3 振动标线设置对连续梁桥动力响应影响研究

3.1 工况选取

通过调研实桥设置振动标线的一般情况,本文振动标线设置组数分别为N=4、5、6,间隔按d=4.0 m、4.5 m、5.0 m、5.5 m、6.0 m考虑,首条振动标线距梁端距离分别按D=4 m、6 m、8 m计算。本文研究对象为山区交通下坡路段,而目前山区公路限速多为60～80 km/h,虽然车速对冲击系数影响较大,但已有文献[18]表明车速、车型与车重耦合后对冲击系数的影响结论不统一,故此处取中间段速度v=20 m/s=72 km/h,合计135个工况,为避免桥面不平顺度样本的随机性对结果造成的影响,桥梁在相同减速带布置情况下分别取20种不平顺度工况,对其冲击系数求均值。具体分析工况如表2所示。

(a) 示意图(mm)

(b) 实桥图

表2 连续梁桥振动标线分析工况

3.2 振动标线设置组数对连续梁桥动力响应影响研究

在分析过程中保持振动标线组间距d、车速v及距梁端距离D不变,只改变标线数量,组数分别为N=4、5、6。以2×30 m跨径布置,D=4 m,d=4.0 m为例,第一跨跨中及第二跨跨中挠度时程曲线结果如图6所示,其中挠度以向下为正。

由图6可知：

(1) 首个振动标线距梁端距离D和振动标线组间距d相同时,在不同组数振动标线下相同跨中位置处挠度时程曲线在0～1.7 s基本重合,而在1.7～3 s出现偏差(曲线不再重合);原因在于在N=4基础上增加组数导致桥面不平顺度的动力效应叠加。

图6 不同截面位置挠度时程曲线

(2) 不同跨中位置处挠度时程曲线在2～3 s范围内波动较大,原因在于此时车辆行驶在第二跨跨内,而当车辆从桥梁第一跨移动到第二跨时,桥梁第二跨梁已经存在初始振动,故挠度时程曲线波动较大。

通过挠度时程曲线,依据式(3)计算最大挠度对应的冲击系数。

即

(3)

式中：Adyn为车辆通过桥梁时跨中动挠度(应变)峰值;Ast为同一车辆静止作用于跨中时对应的最大静挠度(应变)值。

同时该桥基频按JTG D60—2015《公路桥涵设计通用规范》计算值为

(4)

代入式(3)可得冲击系数计算值为μ=0.207。

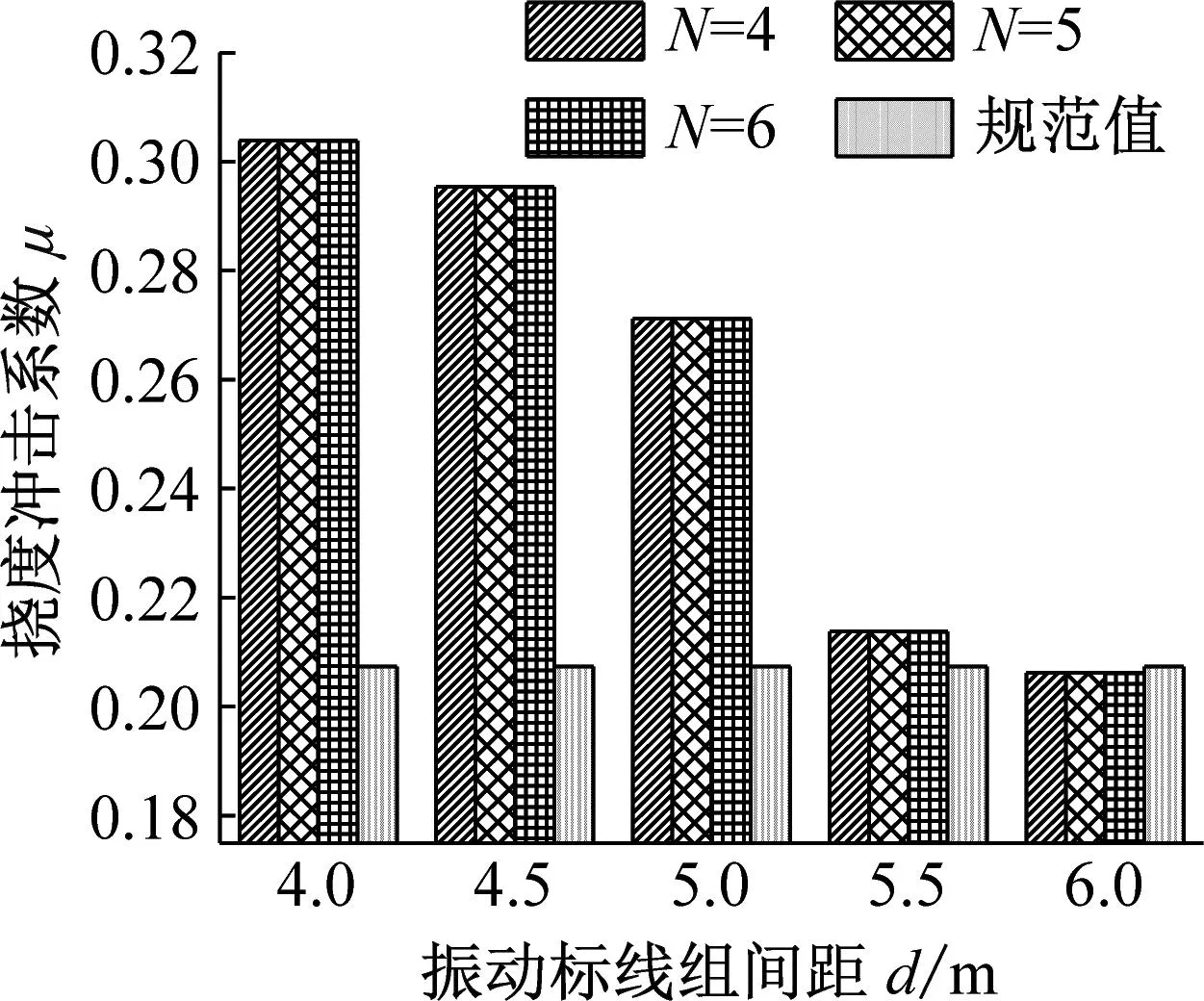
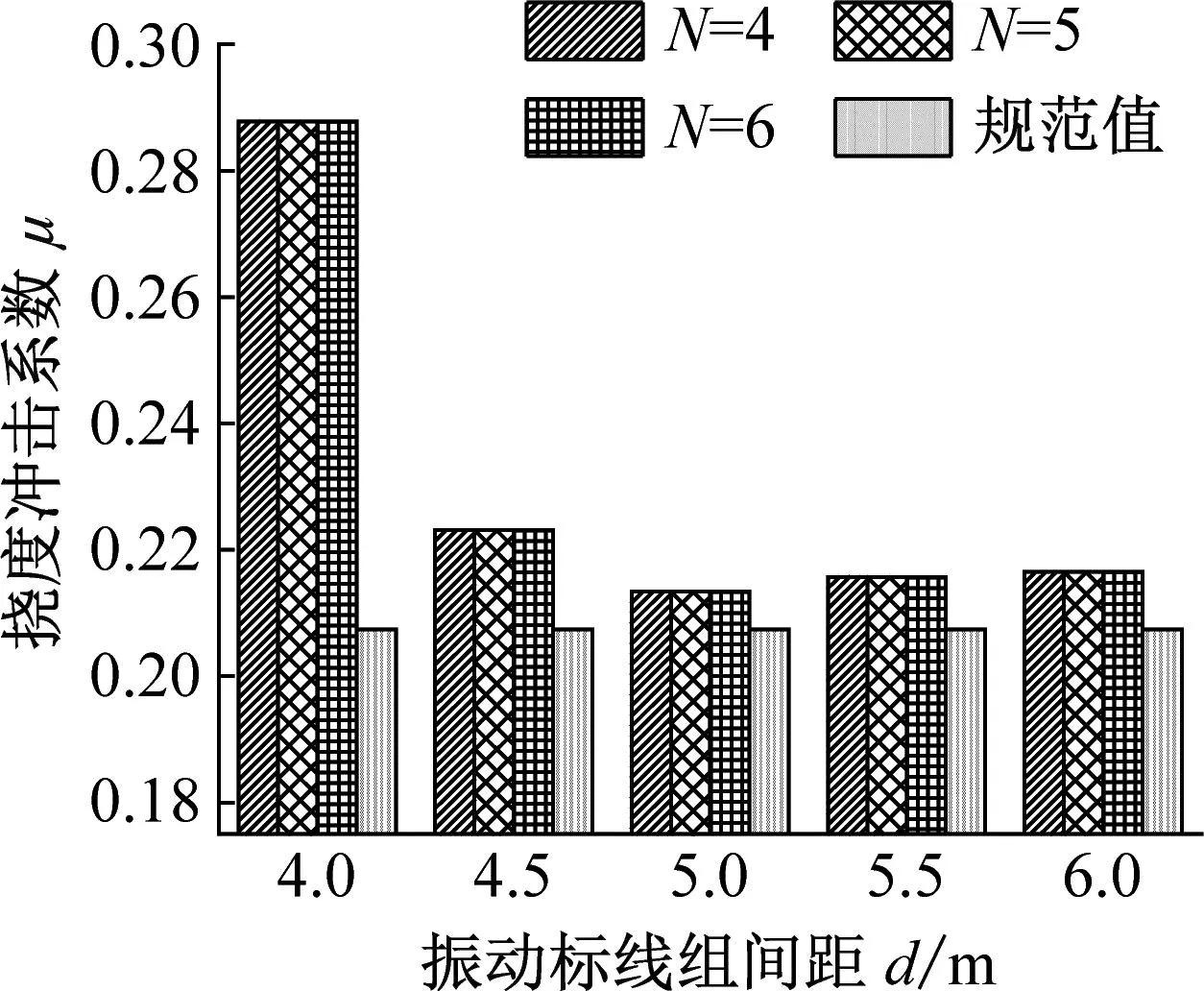
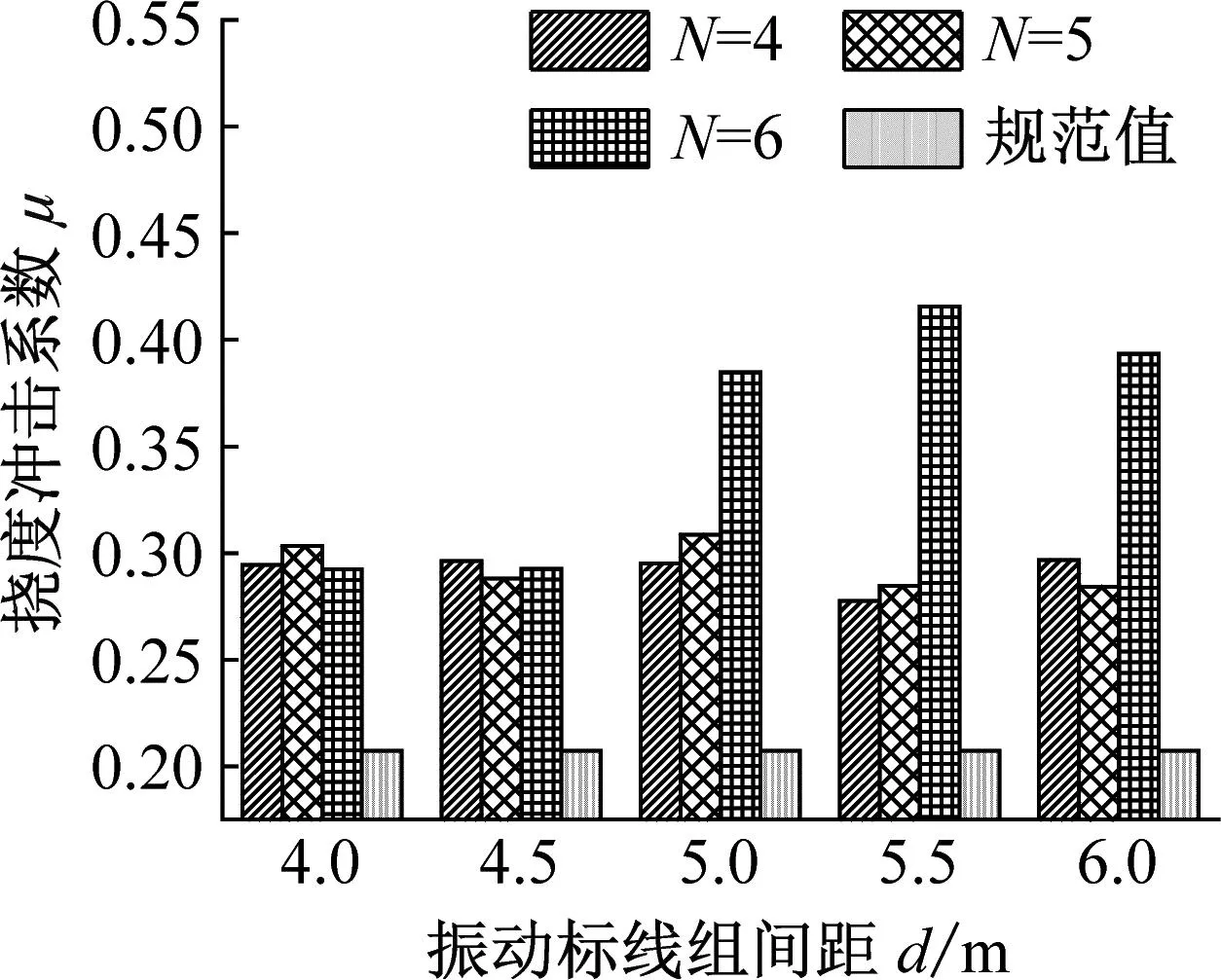
当距梁端距离D和组间距d相同时,不同振动标线组数分别按照式(3)计算冲击系数,并与规范值进行对比如图7～9所示。

由图7～9可知：

(1) 对于第一跨跨中挠度冲击系数,不同跨径布置下振动标线组数设置的变化对其影响不大,仅在数值上随着组数的增加有微小的上下波动,并且规律性较弱;原因在于按振动标线组数N=4、组间距d=4.0 m及距梁端距离D=4 m时,振动标线满布于第一跨跨内,后续增加组数布置于第二跨路段,所以振动标线组数的增加对于第一跨跨中挠度冲击系数影响较小。

(2) 对于第二跨跨中挠度冲击系数,在不同跨径布置下,随着振动标线设置组数的增大,其发生较大变化,当振动标线组数N=6时,冲击系数基本达到最大。这是由于相较振动标线组数N=4时,后续振动标线组数的增加主要布置于第二跨跨内,加剧了第二跨跨内桥面不平顺度,所以振动标线组数的增加对于第二跨跨中挠度冲击系数影响较大。

(a) D=4 m

(b) D=6 m

(c) D=8 m

(a) D=4 m

(b) D=6 m

(c) D=8 m

(a) D=4 m

(b) D=6 m

(c) D=8 m

(a) D=4 m

(c) D=8 m

(a) D=4 m

(b) D=6 m

(c) D=8 m

(a) D=4 m

(b) D=6 m

(3) 对比规范法计算挠度冲击系数值可知,在合计135个工况中共计有120个工况下第一跨跨中挠度冲击系数大于规范值,最大为规范值的1.58倍;第二跨跨中挠度冲击系数均大于规范值,最大为规范值的2.40倍。

综上可知,振动标线组数的变化对于连续梁桥挠度冲击系数有显著的影响。且对于连续梁桥不同跨而言,振动标线组数的变化对挠度冲击系数的影响各有不同,第二跨挠度冲击系数对振动标线组数的变化更加敏感。

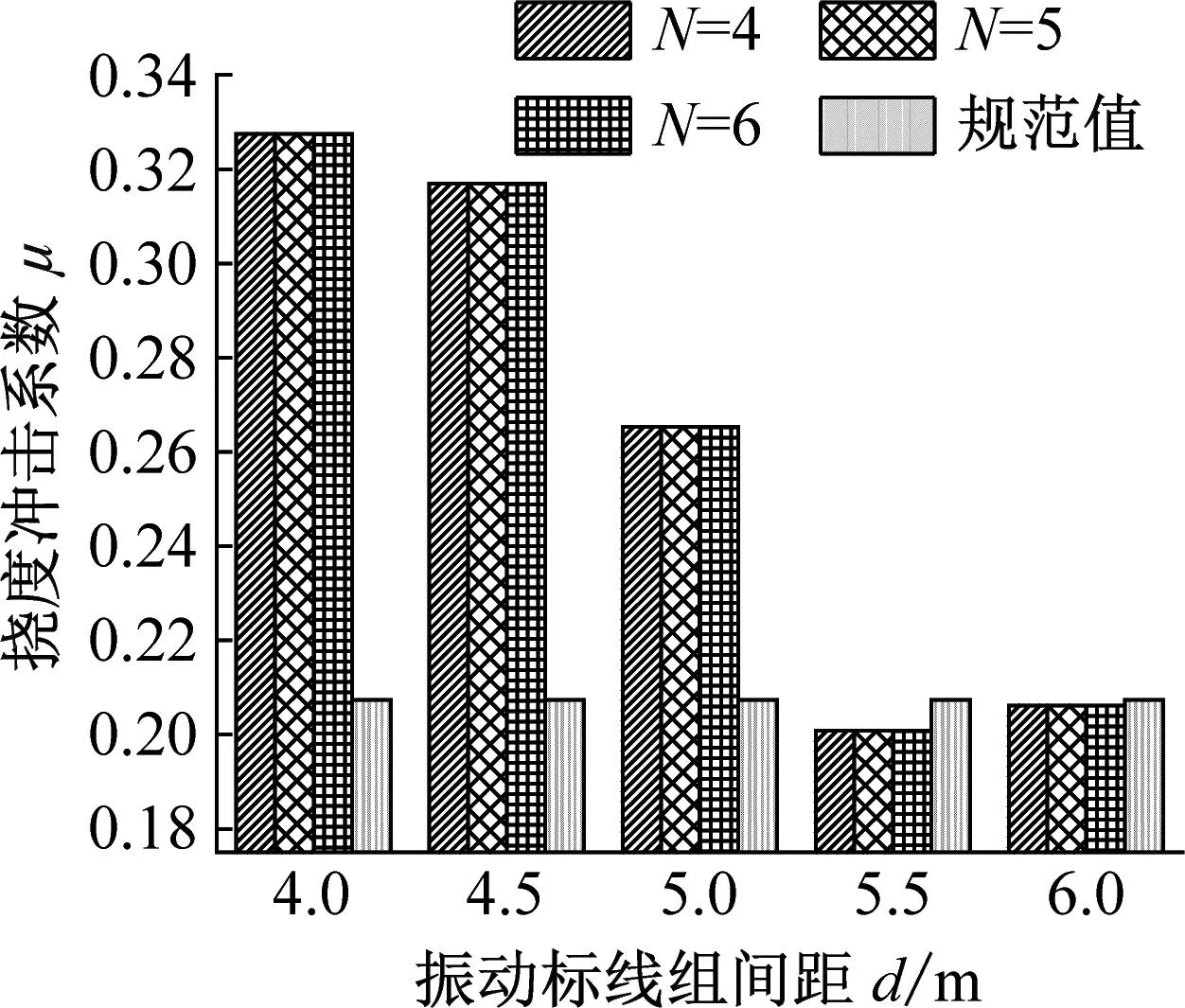
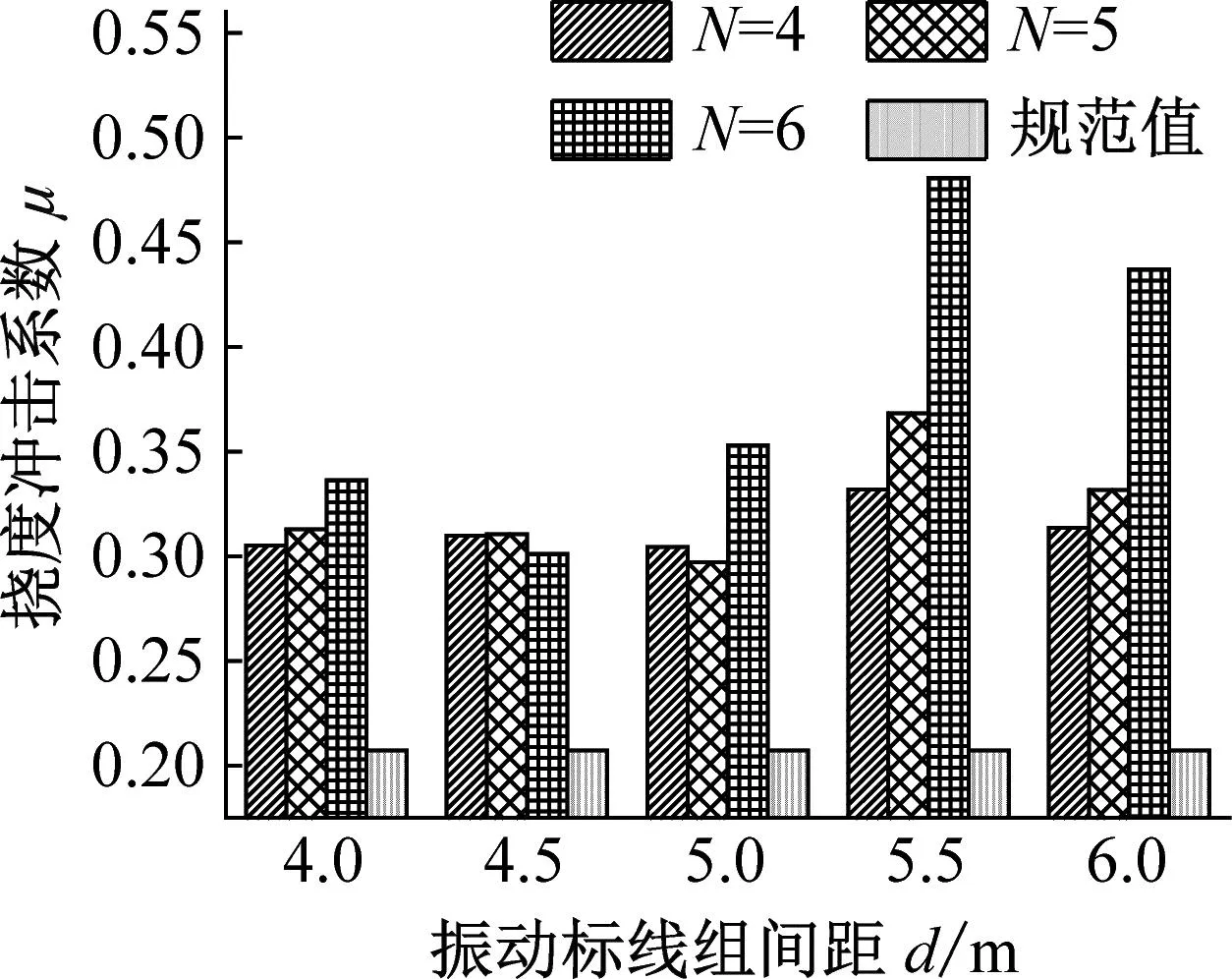
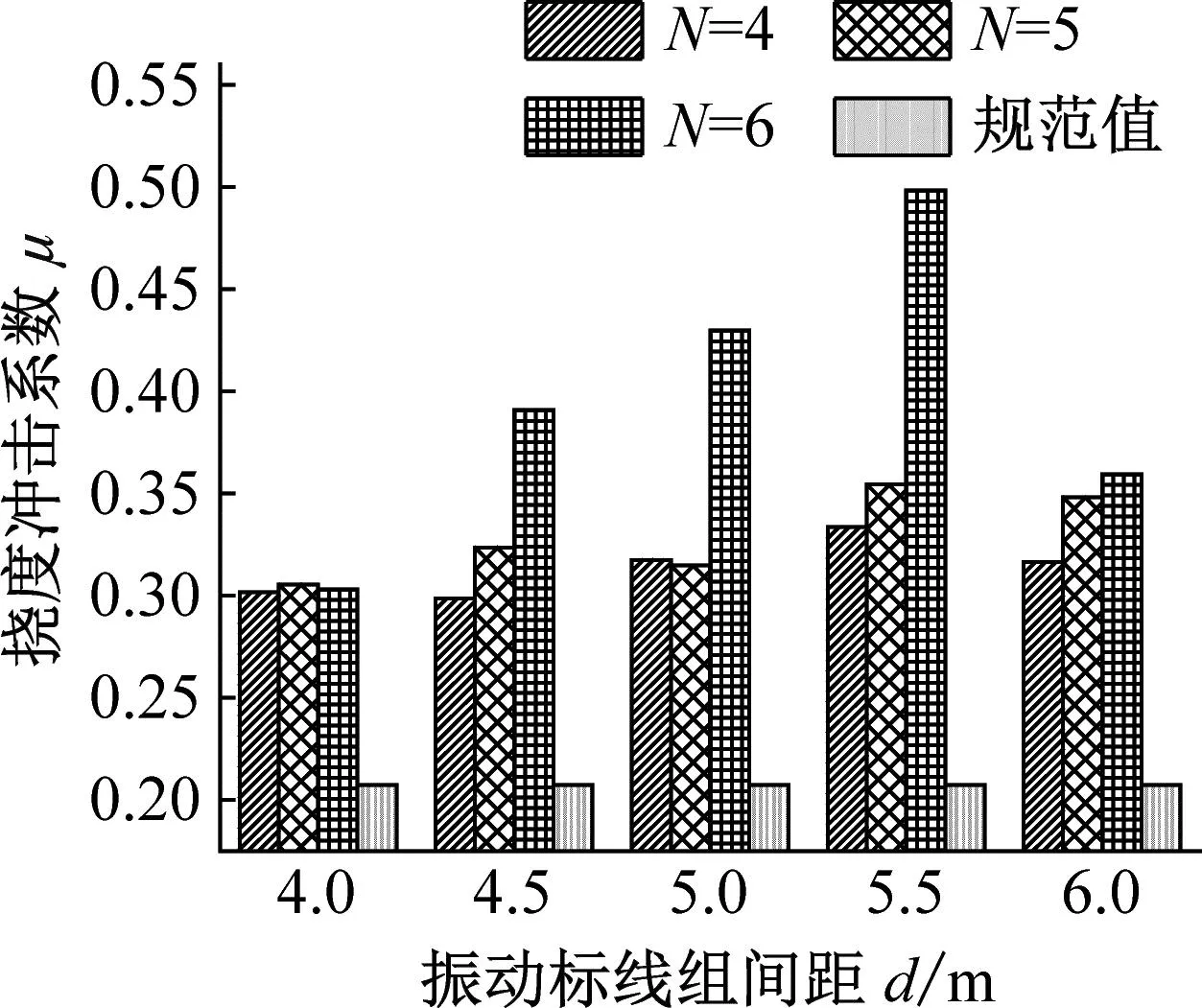
3.3 振动标线组间距对连续梁桥动力响应影响研究

为了研究振动标线组间距对连续梁桥冲击系数的影响,在分析过程中保持振动标线组数N和距梁端距离D相同,只改变其组间距,大小分别为d=4.0 m、4.5 m、5.0 m、5.5 m、6.0 m。

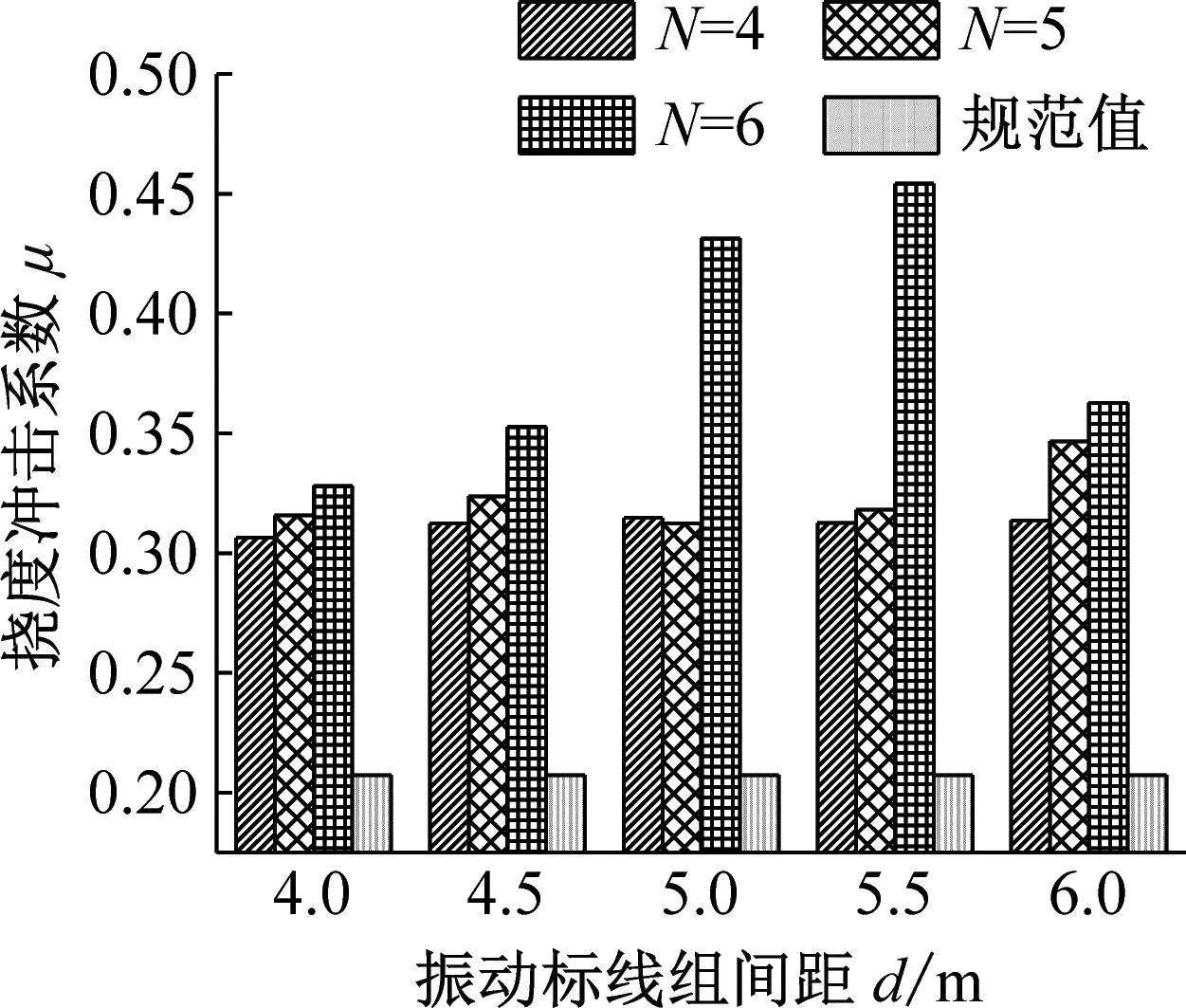
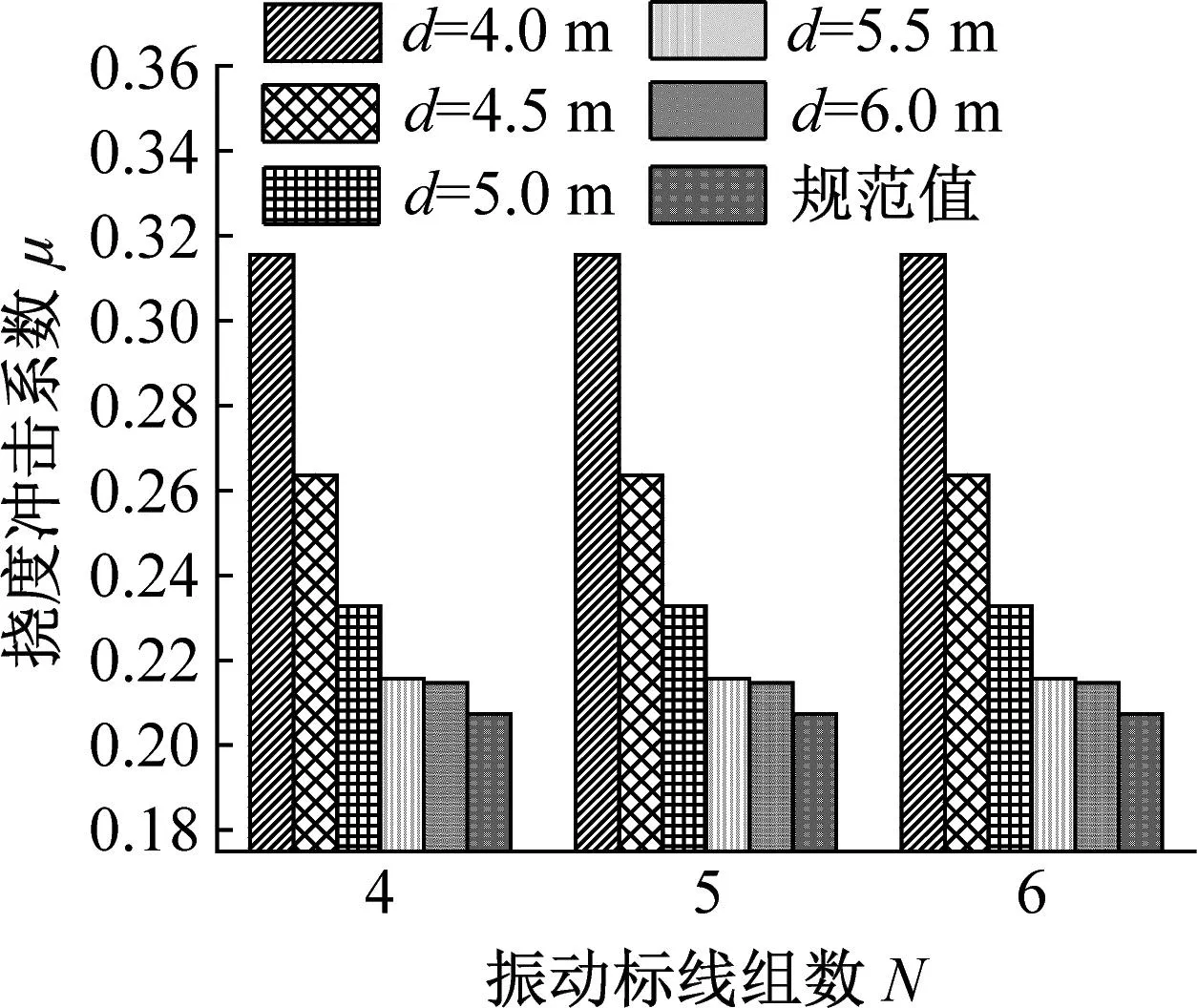
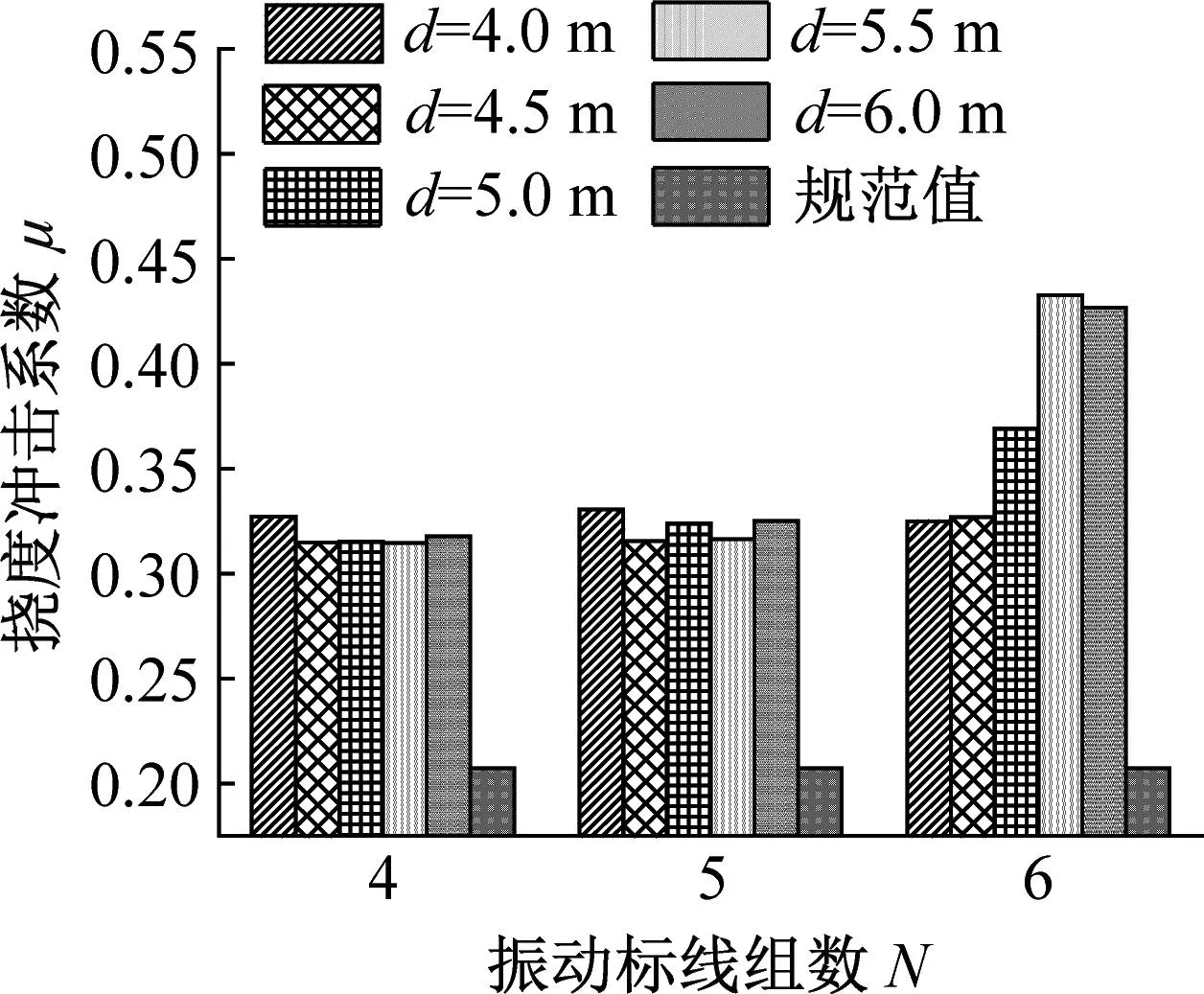
在距梁端距离D和组数N相同的条件下,按传统计算方法得到不同振动标线组间距下的冲击系数,并与规范值进行对比,限于篇幅设置,下文仅示意2×30 m及3×30 m跨径计算结果,如图10～11所示。

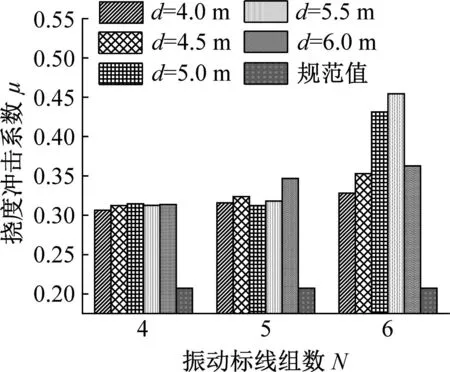
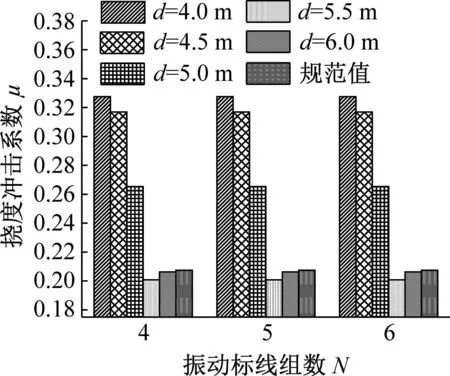
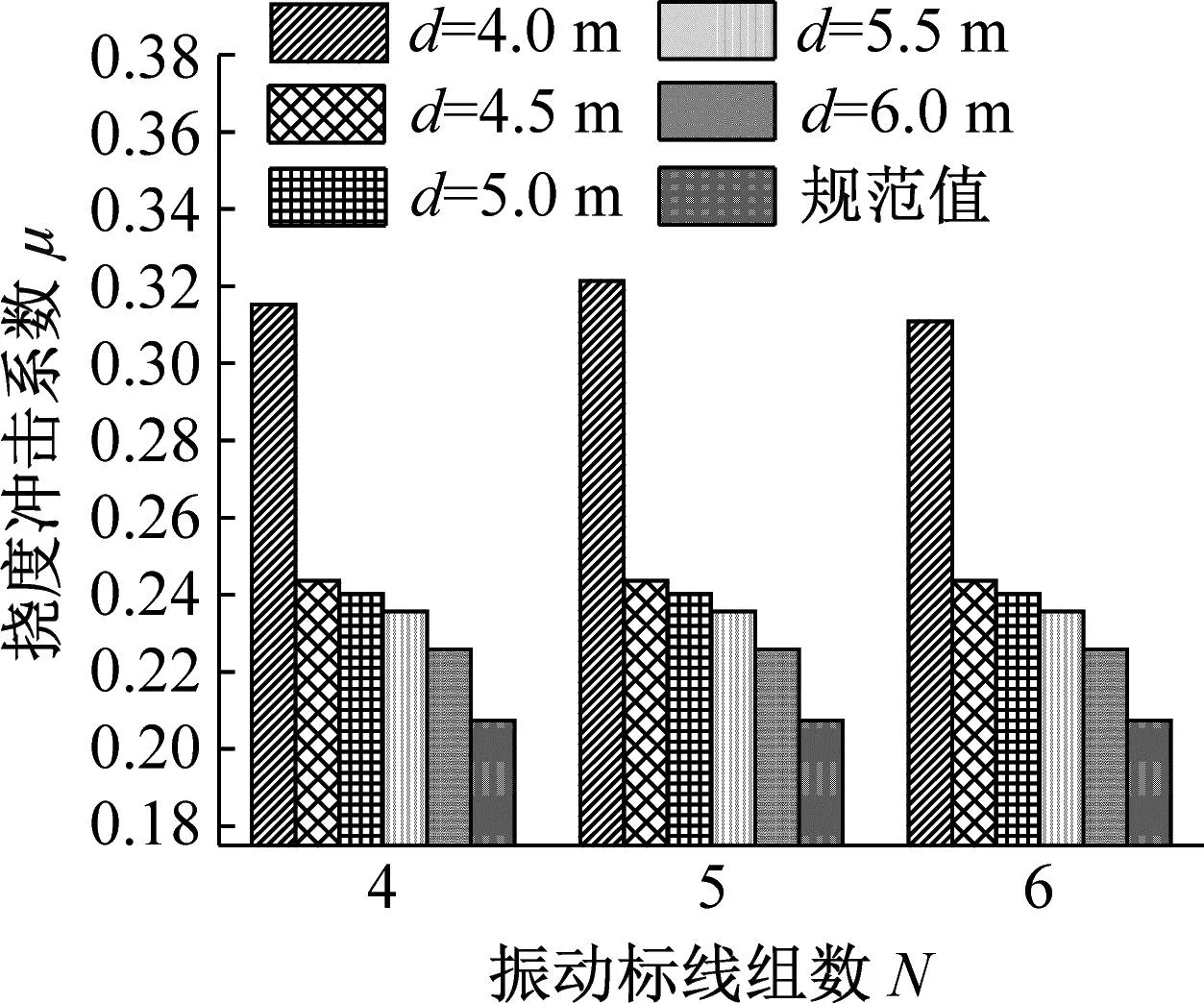
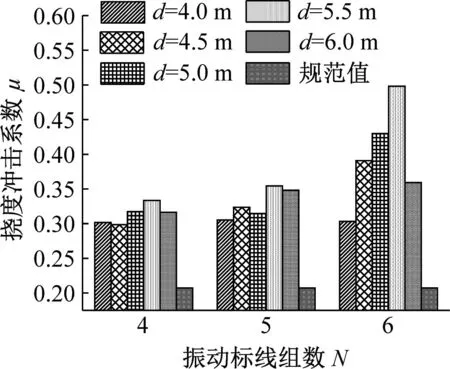
由图10～11可知：

(1) 对于第一跨跨中挠度冲击系数而言,不同的跨径布置下,其随着振动标线组间距变化而发生较大变化,且在不同距梁端距离D和振动标线组数N的情况下变化比较复杂;当距梁端距离D=4 m,振动标线组数N相同的情况下,不同跨径布置冲击系数达到最大值时振动标线组间距d不同,2×30 m和4×30 m跨径布置下振动标线组间距d=5.0 m时第一跨跨中挠度冲击系数最大,3×30 m跨径布置下振动标线组间距d=5.5 m时第一跨跨中挠度冲击系数最大;当距梁端距离D=6 m和8 m,振动标线组数N相同的情况下,振动标线组间距d=4.0 m时第一跨跨中挠度冲击系数最大。

(2) 对于第二跨跨中挠度冲击系数而言,当振动标线组数N=4和5时,挠度冲击系数随着振动标线组间距的变化而变化,但变化幅度较小,当振动标线组数N=6时,挠度冲击系数随着振动标线组间距的变化而发生较大变化,原因在于当振动标线组数N=6时,随着振动标线组间距的增大,振动标线布置逐渐靠近第二跨跨中位置,对第二跨跨中位置挠度冲击系数影响加大,故冲击系数变化较大。

综上可知,振动标线组间距的改变显著影响桥梁冲击系数,且对于连续梁桥不同位置而言,振动标线组间距的变化对挠度冲击系数的影响各有不同。在距梁端距离D相同,第一跨跨中挠度冲击系数随振动标线组间距变化规律性较强。

(a) D=4 m

(b) D=6 m

(c) D=8 m

(a) D=4 m

(b) D=6 m

(c) D=8 m

(a) D=4 m

(b) D=6 m

(c) D=8 m

(a) D=4 m

(b) D=6 m

(c) D=8 m

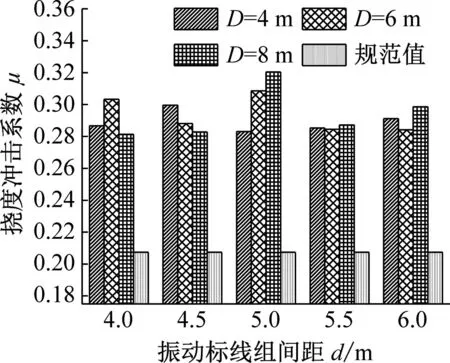
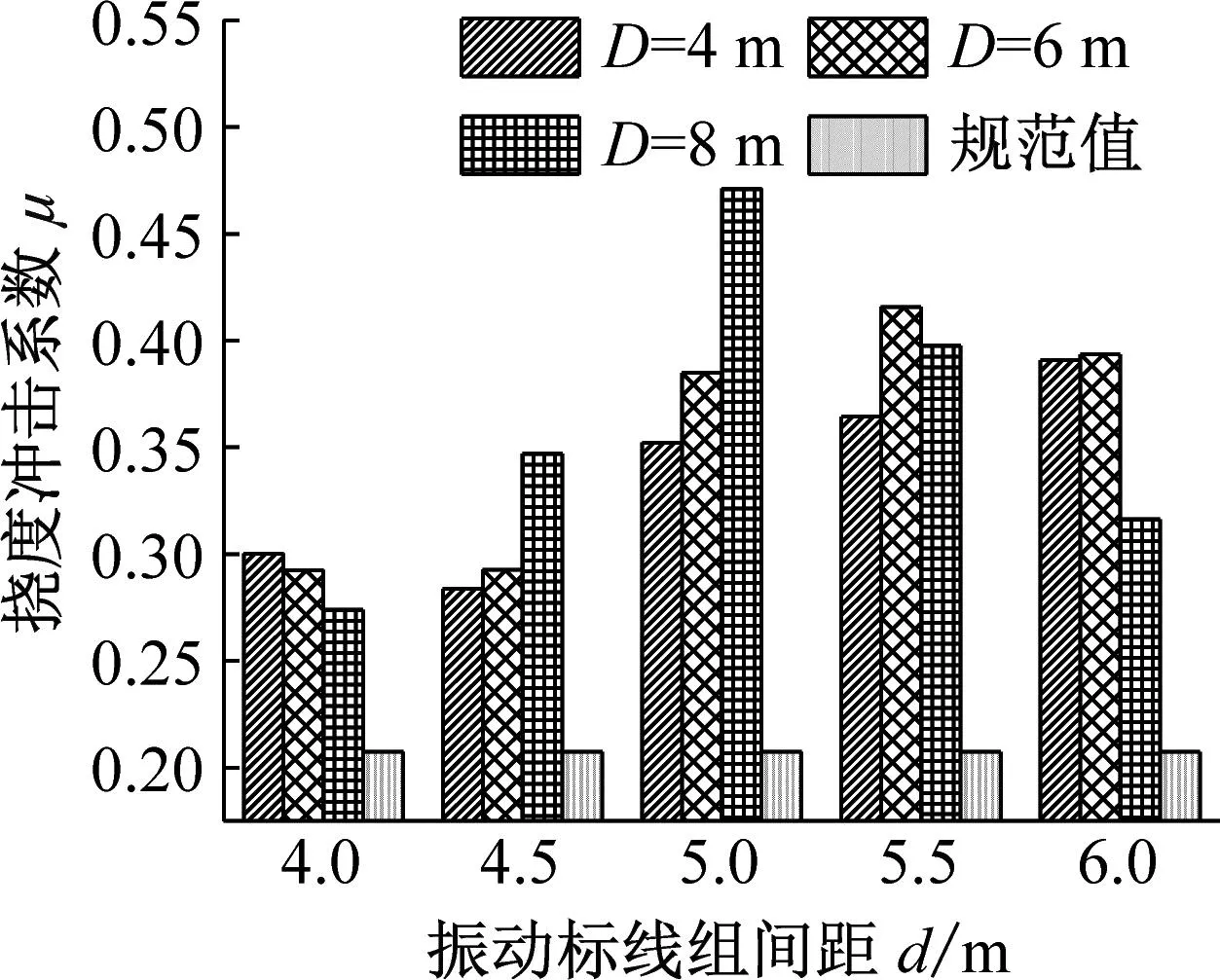
3.4 振动标线设置位置对连续梁桥动力响应的研究

为了研究振动标线设置位置对连续梁桥冲击系数的影响,在分析过程中保持振动标线组数N和组间距d相同,只改变其设置位置,其距梁端距离分别为D=4 m、6 m、8 m。

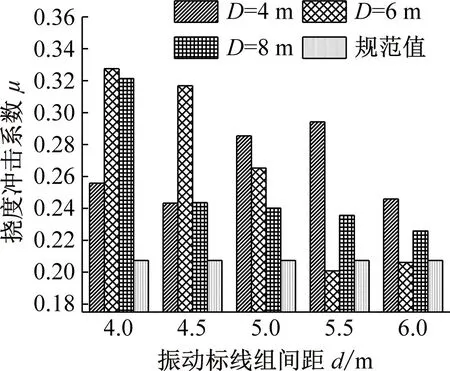
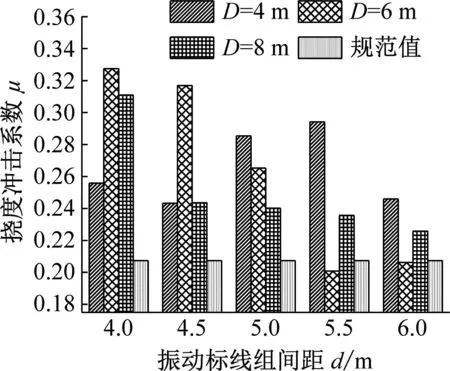
分别按传统计算法和规范法计算振动标线组间距d和组数N相同的条件下,不同振动标线设置位置下的挠度冲击系数。以下列举3×30 m及4×30 m跨径布置计算结果,如图12～13所示。

(a) N=4

(b) N=5

(c) N=6

(a) N=4

(b) N=5

(c) N=6

(a) N=4

(b) N=5

(c) N=6

(a) N=4

(b) N=5

(c) N=6

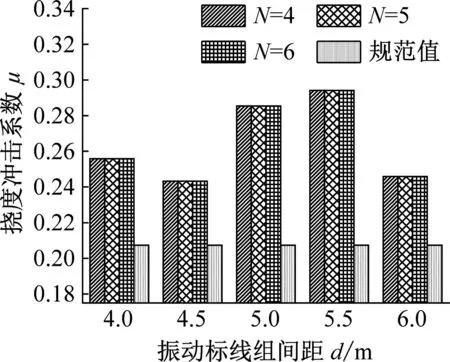
由图12～13可知：

(1) 对于第一跨跨中挠度冲击系数,距梁端距离的改变对挠度冲击系数有一定的影响,且对比可知,当振动标线组间距d=4.0 m、4.5 m、5.0 m和5.5 m时,不同跨径布置下挠度冲击系数随着距梁端距离D变化规律相同,振动标线组间距d=4.0 m和4.5 m时,距梁端距离D=6 m的情况下第一跨跨中挠度冲击系数最大,振动标线组间距d=5.0 m和5.5 m时,距梁端距离D=4 m的情况下第一跨跨中挠度冲击系数最大;当振动标线组间距d=6.0 m时,不同跨径布置下挠度冲击系数随着距梁端距离D变化规律不同,2×30 m和3×30 m跨径布置下距梁端距离D=4 m时第一跨跨中挠度冲击系数最大,4×30 m跨径布置下距梁端距离D=6 m时第一跨跨中挠度冲击系数最大。

(2) 对于第二跨跨中挠度冲击系数,距梁端距离的改变对挠度冲击系数有一定的影响,当振动标线组数N=4和5时,挠度冲击系数随振动标线设置位置D的变化而变化的幅度较小,且变化比较复杂;当振动标线组数N=6,组间距d=5.0 m,挠度冲击系数随振动标线设置位置D的增大而增大,其中4×30 m跨径布置下挠度冲击系数随振动标线设置位置D增大而增大的幅度最大。

(3) 对比第一跨、第二跨跨中位置挠度冲击系数值可知,第一跨跨中挠度冲击系数对振动标线设置位置D的变化相对于第二跨跨中挠度冲击系数更加敏感。

综上可知,振动标线距梁端位置的改变可影响桥梁冲击系数,第一跨跨中位置及第二跨跨中位置挠度冲击系数随距梁端距离D的改变均有显著变化。

3.5 振动标线合理设置的措施建议

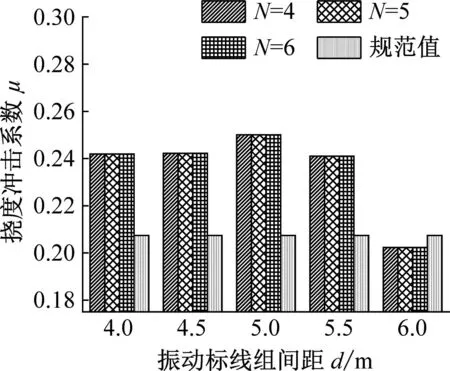
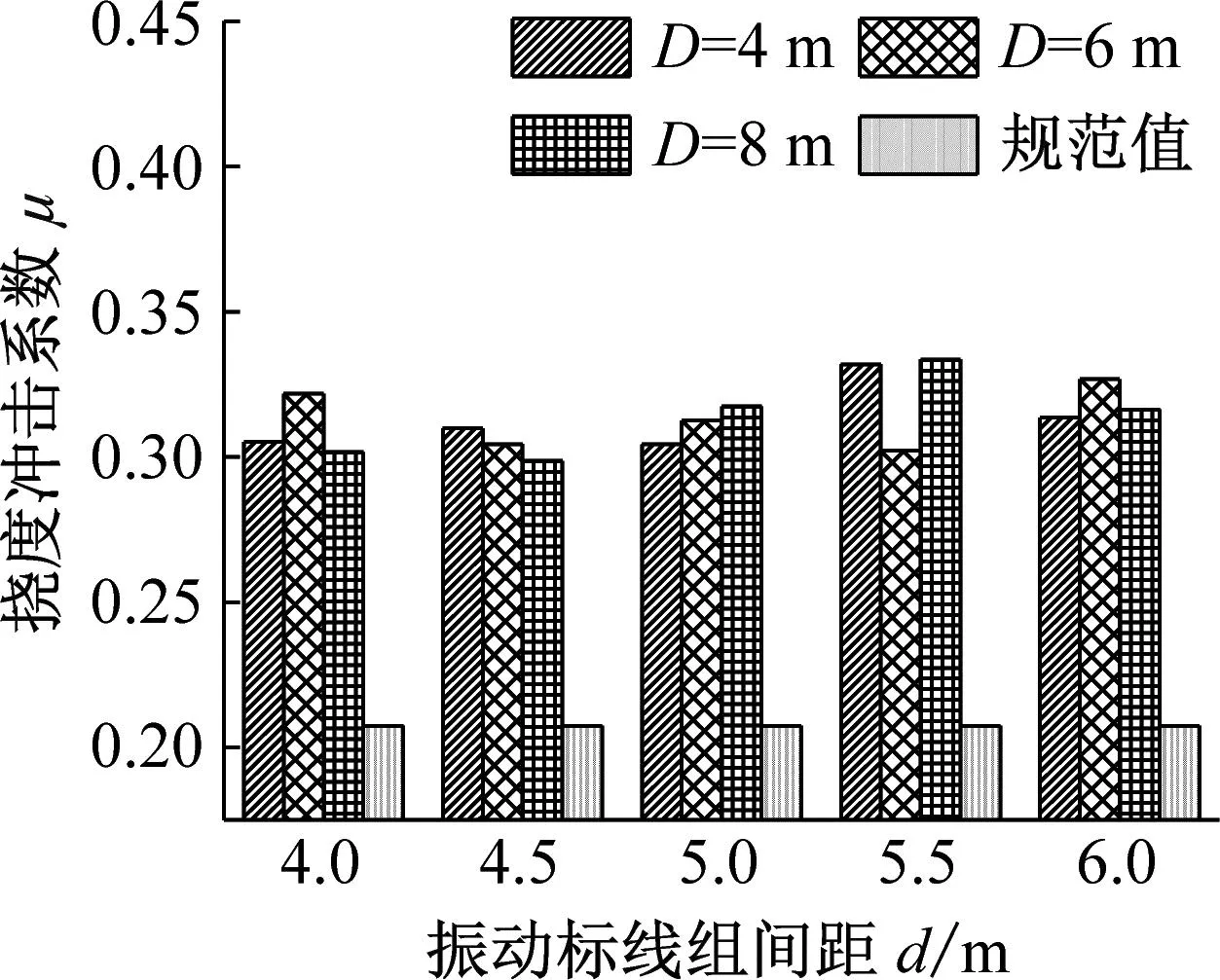
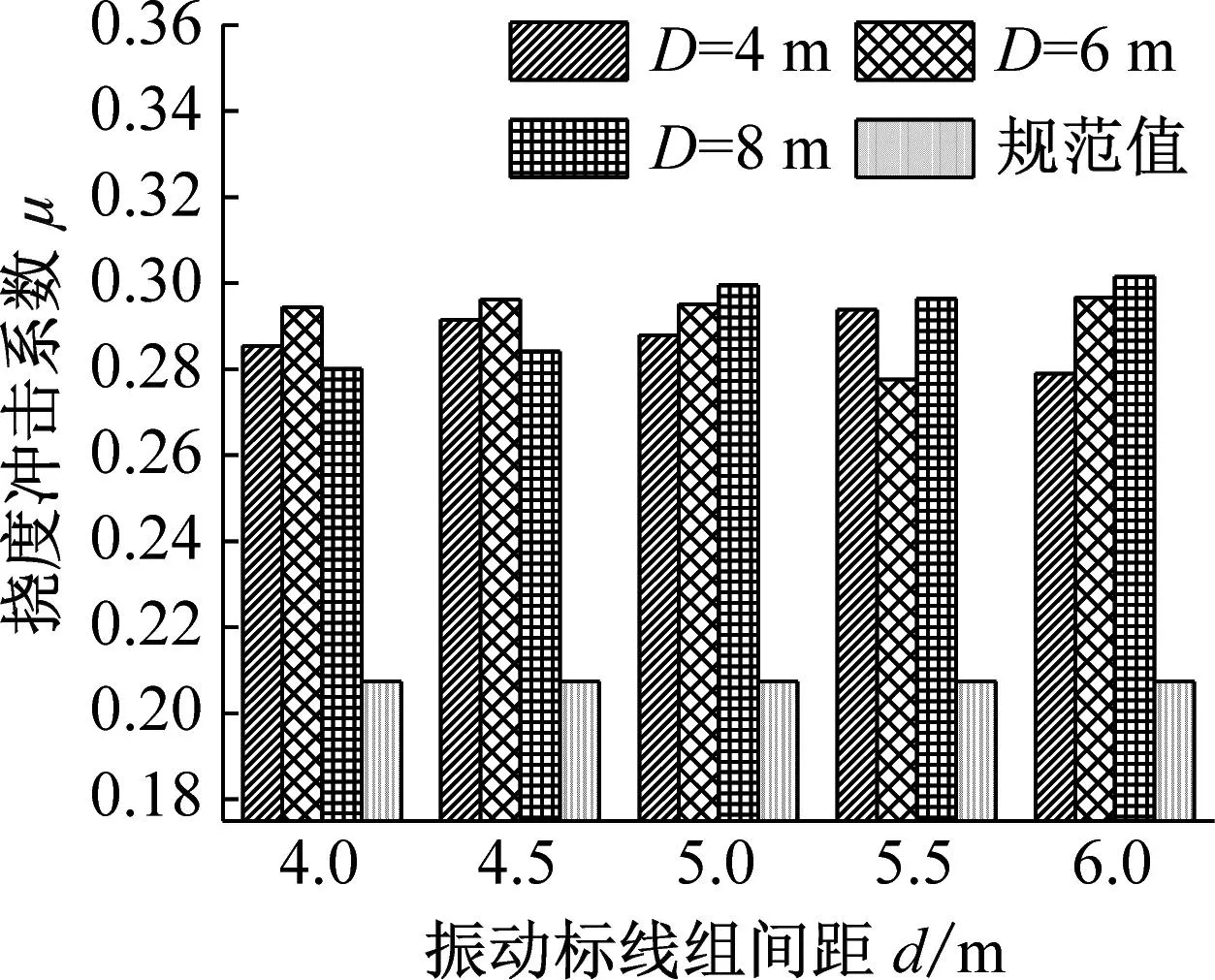
综上所述,振动标线的组数,组间距以及设置的位置对桥梁挠度冲击系数有显著影响。综合以上分析数据,提出连续梁桥振动标线设置的合理建议。取同一振动标线布置条件下不同跨中位置挠度冲击系数最大值进行对比,分析结果如图14～16所示。

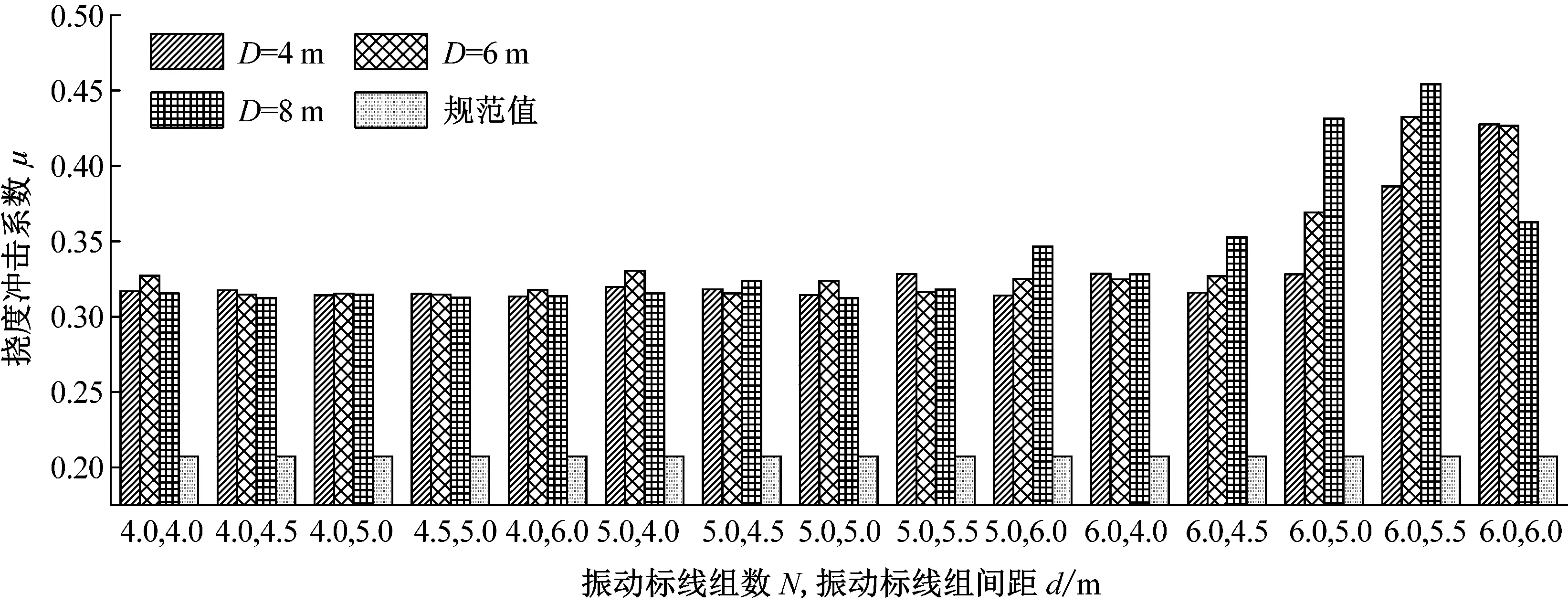
图14 2×30 m跨径布置下挠度冲击系数综合对比

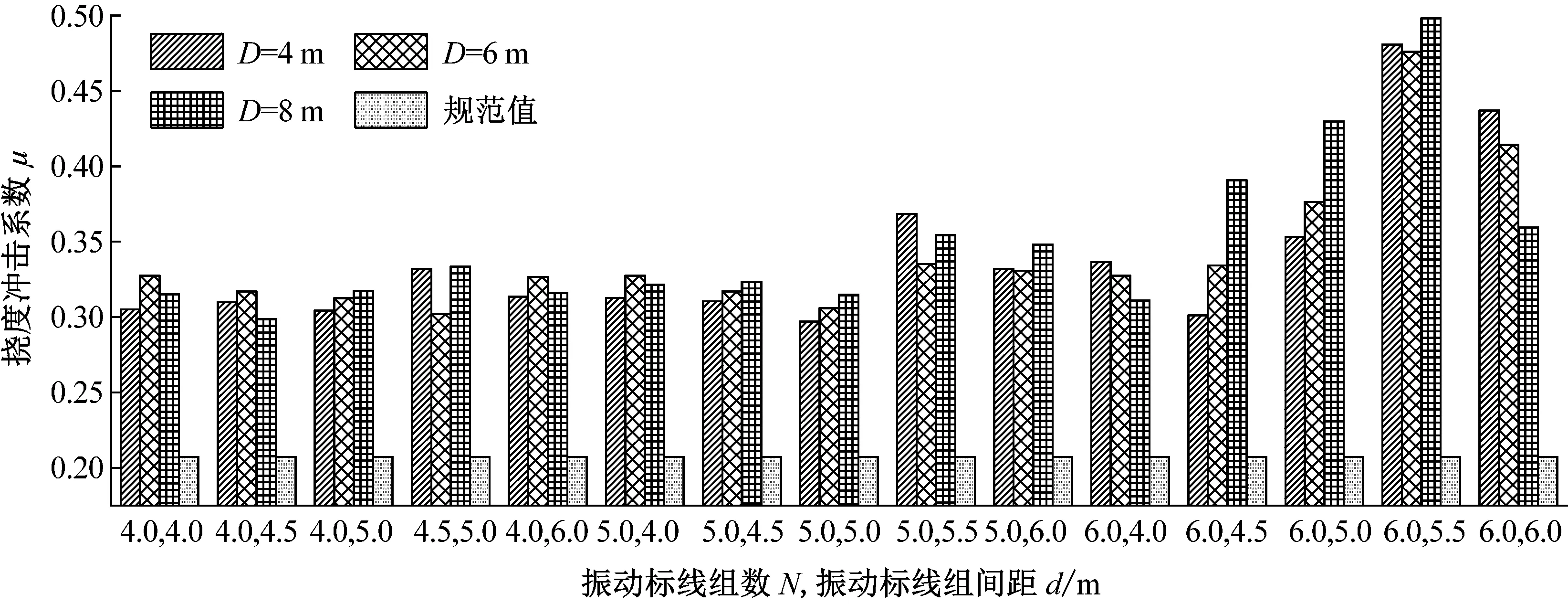
图15 3×30 m跨径布置下挠度冲击系数综合对比

由图14～16可知：

(1) 对于2×30 m连续梁桥挠度冲击系数,由3.2节结论可知,第一跨跨中位置挠度冲击系数对组数的变化不敏感,故根据振动标线实际需求组数参考第二跨跨中挠度冲击系数进行选择。在相同振动标线组数的条件下,选取挠度冲击系数最小时的振动标线据梁端位置D及组间距d布置情况。当振动标线组数要求N=6时,建议选择振动标线距梁端距离D=4 m,组间距d=4.5 m的设置形式;当振动标线组数要求N=5时,建议选择振动标线距梁端D=8 m,组间距d=5.0 m的设置形式;当振动标线组数要求N=4时,建议选择振动标线距梁端D=4 m,组间距d=6.0 m的设置形式。

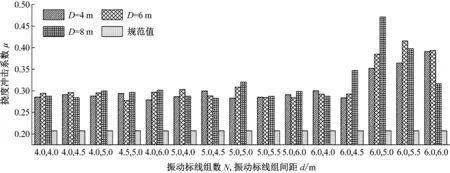
图16 4×30 m跨径布置下挠度冲击系数综合对比

(2) 对于3×30 m连续梁桥挠度冲击系数：当振动标线组数要求N=6时,建议选择振动标线距梁端距离D=4 m,组间距d=4.5 m的设置形式;当振动标线组数要求N=5时,建议选择振动标线距梁端D=4 m,组间距d=5.0 m的设置形式;当振动标线组数要求N=4时,建议选择振动标线距梁端D=8 m,组间距d=4.5 m的设置形式。

(3) 对于4×30 m连续梁桥挠度冲击系数：当振动标线组数要求N=6时,建议选择振动标线距梁端距离D=4 m,组间距d=4.5 m的设置形式;当振动标线组数要求N=5时,建议选择振动标线距梁端D=8 m,组间距d=4.5 m的设置形式;当振动标线组数要求N=4时,建议选择振动标线距梁端D=6 m,组间距d=5.5 m的设置形式。

综上可知,结合不同跨径下布置建议,根据振动标线设置组数需求,当振动标线组数N=6,选择距梁端距离D=4 m,组间距d=4.5 m的设置形式,当振动标线组数N=4和5时,需根据不同跨径布置选择不同的振动标线设置形式,此时冲击系数在不同距梁端距离D和组间距d的工况下的均值为0.28,为规范值的1.35倍。

4 结 论

通过对有限元模型的计算和分析,研究振动标线设置组数、组间距以及位置对连续梁桥挠度冲击系数的影响,对比分析规范冲击系数计算值,得出结论如下：

(1) 设置振动标线后连续梁桥挠度冲击系数均大于规范值,最大为规范值的2.40倍,在有振动标线设置需求路段桥梁,需考虑振动标线对桥梁结构冲击系数的影响。

(2) 振动标线在桥梁上的位置、数量、组间距的改变对挠度冲击系数均有显著影响,且对于连续梁桥不同位置的挠度冲击系数影响程度不同。其中第二跨跨中位置挠度冲击系数较第一跨跨中对振动标线组数的变化更加敏感,第一跨跨中位置挠度冲击系数较第二跨跨中对振动标线设置位置的变化更加敏感。

(3) 在振动标线设置组数一定的条件下,通过对连续梁桥不同位置挠度冲击系数受振动标线不同数量、不同组距及布置位置等影响因素的研究,建议当振动标线组数N=6时,选择距梁端距离D=4 m,组间距d=4.5 m的设置形式,当振动标线组数N=4和5时,需根据不同跨径布置选择不同的振动标线设置形式。