高应变率荷载作用下钢筋与ECC的黏结滑移关系研究

崔双双, 孟 瑶, 陈伟宏, 孙 浩

(1.福建理工大学 地下工程福建省高校重点实验室,福州 350118; 2.福建理工大学 土木工程学院,福州 350118; 3.福州大学 土木工程学院,福州 350116)

钢筋混凝土结构被广泛应用于建筑工程中,但混凝土是一种脆性材料,延性差,吸能低,在爆炸、冲击等高应变率荷载作用下,结构的竖向承重构件会发生破坏,进而导致连续倒塌破坏。工程用水泥基复合材料(engineering cementitious composite,ECC)具有较高的延性、明显的应变硬化及多缝开裂特征,可替代混凝土来提高结构延性、抗冲击性及抗连续倒塌能力。当结构进入悬链线大变形阶段时,ECC与钢筋之间可能会产生黏结滑移,导致两者之间协同工作能力变差,降低结构性能,定量分析高应变率荷载作用下钢筋与ECC之间的黏结滑移性能,并得到其精确的黏结滑移本构,对准确分析结构的抗连续倒塌能力至关重要,是ECC构件设计及有限元分析的理论基础。

近年来,国内外学者对筋材-ECC的黏结滑移性能进行了相关研究,但大多基于静态试验。姜天华等[1]通过中心拉拔试验研究了钢纤维掺量、锚固长度、钢筋直径对玄武岩纤维增强树脂复合材料(basalt fiber reinforced composite, BFRP)筋与钢-PVA混杂ECC黏结性能的影响,研究表明试件的黏结强度随钢纤维掺量的增加而增加,随BFRP筋直径、锚固长度的增加而减小。Lee等[2]通过对比试验研究比较了混凝土、ECC两种材料与钢筋之间的黏结滑移性能,发现ECC材料的黏结滑移性能优于混凝土材料。

而ECC、钢筋都是率敏感性材料,其力学性能、变形性能及本构关系均会随着荷载应变率发生变化。宋国杰[3]和Xu等[4]分别研究了加载速率对钢筋与再生混凝土、钢筋与混凝土之间的黏结滑移性能的影响,发现试件的黏结强度会随加载速率的增加而增加。付应乾等[5]通过中心拉拔试验发现应变率提高钢筋-混凝土试件的黏结强度明显增大。周继凯等[6]对高应力率作用下钢筋与混凝土的黏结性能进行研究发现黏结强度随应力率增加而增加。综上可知目前关于荷载应变率对材料黏结滑移关系的影响研究主要集中在混凝土-钢筋两种材料之间,针对高应变率荷载作用下钢筋-ECC黏结滑移关系的研究很少。

关于黏结滑移关系的研究通常是指平均黏结应力与加载端部的相对滑移之间的关系,但实际工程中,黏结应力是随着锚固位置不断变化的。徐世烺等[7-9]分别建立了静力荷载下考虑位置影响的钢筋与超高韧性水泥基复合材料(ultra high toughness cementitious composite, UHTCC)、再生混凝土以及混凝土之间的黏结滑移本构关系。高应变率下考虑锚固位置影响的钢筋-ECC本构还鲜有研究。

因此,本文进行高应变率荷载下钢筋-ECC的黏结滑移性能试验,分析其破坏模式,获得平均黏结滑移曲线,并与静态下的黏结滑移试验进行对比,最后通过内贴应变片记录试验中不同锚固位置处钢筋的应变及两者间的黏结应力、相对滑移分布规律,进而建立考虑锚固位置影响的钢筋-ECC黏结滑移本构关系。

1 高应变率荷载作用下钢筋与ECC的黏结滑移试验研究

1.1 材料属性

试验采用的钢筋型号为HRB400,直径分别为14 mm、18 mm、22 mm,参照规范GBT 228.1—2010《金属材料拉伸试验》的相关规定对钢筋进行力学性能测试,HRB400钢筋基本力学性能实测参数如表1所示。

表1 钢筋力学性能表

ECC由42.5级的普通硅酸盐水泥、石英砂、I级优质粉煤灰、矿渣粉、聚羧酸型减水剂及2%掺量的PVA(聚乙烯醇)纤维和水制备而成。PVA纤维性能指标如表2所示。

表2 PVA纤维性能指标

试验使用课题组前期试验中得到的较优配合比中的三个强度等级(用E1、E2、E3表示)进行试件ECC基体制备,所用配合比如表3所示。将试块养护28天后进行立方体抗压强度测试,测得E1、E2、E3混凝土抗压强度平均值分别为49.1 MPa、57.7 MPa、68.6 MPa。

表3 ECC配合比

1.2 分离式霍普金森压杆试验拉拔试件设计及加载装置

1.2.1 拉拔试件设计

为研究高应变率荷载作用下钢筋与ECC的黏结滑移关系,以应变率、ECC强度、钢筋直径作为试验参数,设计制作了36组中心拉拔试件,每组重复3次,共108个试件。为方便后文表述,试件统一编号为EeDdεε-N,其中E代表ECC强度等级,D代表钢筋直径;ε代表试验时的应变率;N代表每组中试件的编号,试件详细参数如表4所示。以E1D14ε1-02为例,代表此试件的ECC强度为E1强度等级,即49.1 MPa;钢筋的直径为14 mm,应变率为ε1,即953.94 s-1;试件是此试件组中第2个试件,以此类推。

试验选取0.45 MPa、0.50 MPa、0.55 MPa和0.60 MPa四个冲击气压值,通过不同冲击气压获得的不同冲击速度从而获得不同的应变率。根据预试验的结果得到应变率、冲击速度、应变率间的关系,如表5所示。

表4 试件设计参数表

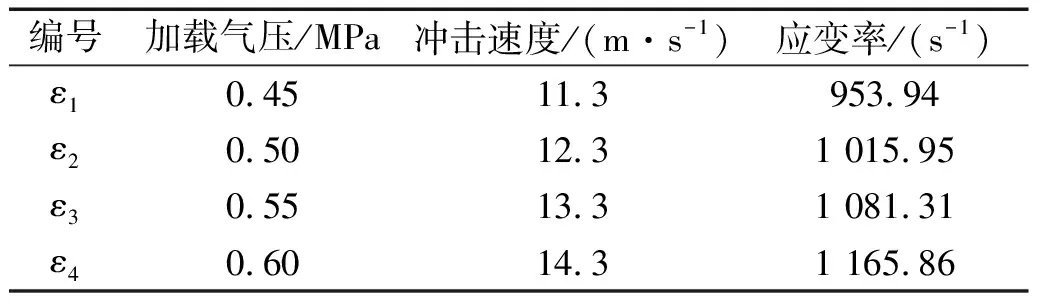
表5 加载气压、冲击速度和应变率关系数值表

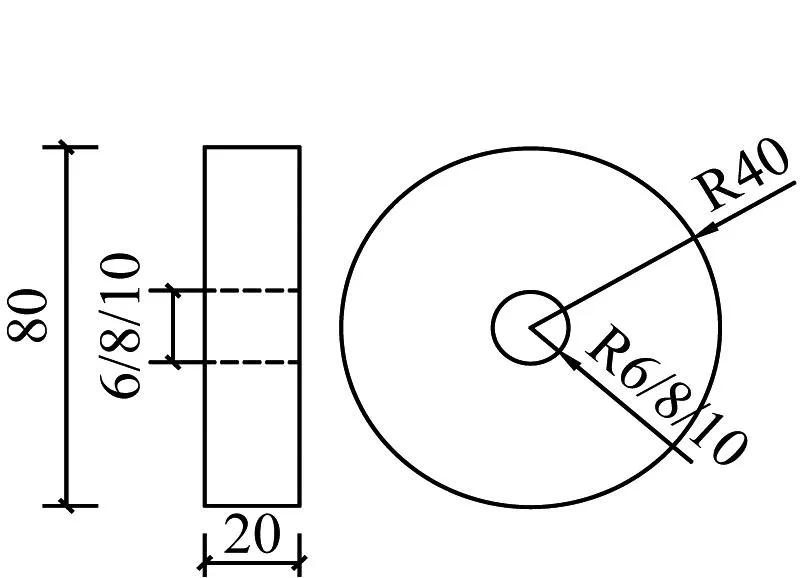
参考中心拉拔试件并结合分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)对试件尺寸的限制,将黏结滑移试件设计为圆柱形中心对称,考虑到SHPB装置的惯性效应和摩擦效应,Gray等[10]指出试件的长径比控制在1.5～2.0时可有效减小摩擦效应。综合上述结论,将圆柱形试件的长径比设计为2.0(钢筋长200 mm,ECC基体直径100 mm),试件相关尺寸如图1所示。右端钢筋为加载端,端部需加工20 mm螺纹以便于后期连接附加装置B,剩余40 mm作为滑移长度,钢筋左端为自由端,左端伸出10 mm以便于应变片导线引出。为尽可能减少因黏结应力不均匀分布造成的影响,钢筋的锚固长度选择为5d,d为钢筋直径。

图1 动态拉拔试件设计简图(mm)

为获得钢筋应变在锚固长度范围内的变化,以方便后续计算不同锚固位置的黏结应力与钢筋-ECC相对滑移量的分布规律,进而建立高应变率荷载作用下考虑位置影响的钢筋-ECC黏结滑移本构关系,试验采用钢筋内贴应变片法,将钢筋沿中心对称轴线加工切开,在钢筋切开面开出2 mm×4 mm(合拢为4 mm×4 mm)的凹槽,应变片沿两部分钢筋间隔交替分布,合拢后应变片间距约20 mm左右,贴片完成后将应变片表面蜡封,之后将钢筋对扣并将应变片导线导出,导线末端标号以记录应变片的位置,然后通过PVC管对钢筋非锚固段进行固定。

1.2.2 SHPB试验加载装置

试验采用直径为80 mm的SHPB试验装置,如图2(a)所示,主要包括直径为80 mm的子弹和压杆,长3 m的入射杆、长2 m的透射杆、长0.5 m的吸收杆以及数据测量和采集系统。试验选用厚度1 mm,直径为20 mm的黄铜片作为波形整形器以消除撞击过程中的高频振荡。

SHPB装置需要安装附加装置才可以进行黏结滑移试验,附加装置可以给试件中的钢筋提供足够的滑移行程,同时可以解决试件的非平面接触问题以及钢筋内部应变片的导出问题。参考相关文献[11]并结合SHPB对试件尺寸的限制,试验设计了附加装置A、B,具体尺寸如图3所示。正式试验开始前需连接好试件与附加装置,见图2(b),附加装置A(图3(a))左端试验时与入射杆连接,右端截面中心预留孔洞以便为钢筋滑移提供变位区间;附件装置B(图3(b))直径与透射杆相同,试验时先插入钢筋螺纹端,右端连接入射杆,该金属装置易加工且易于保证其表面平整度,能极大改善非平面接触问题。

(a) SHPB设备

(b) 附加装置与试件连接

(a) 附加装置A

(b) 附加装置B

试验时,子弹快速撞击入射杆后立即产生入射波εI(t)并向试件传播,传播至入射杆-试件端面时部分入射波在试件左端面反射回入射杆,形成反射波εR(t),另一部分传至透射杆形成透射波,入射杆和透射杆应变片会记录下入射应变εI(t)、反射应变εR(t)和透射应变εT(t)。

1.3 静力黏结滑移对比试验试件设计及试验装置

1.3.1 拉拔试件设计

为方便对比高应变率与静力荷载作用下试件黏结滑移性能区别以及后续计算动态黏结强度增强因子(dynamic increase factor, DIF),试验只考虑了E3强度等级,选取与高应变率荷载作用下黏结滑移试验相同的三种直径钢筋,设计三组静力拉拔试件进行静力黏结滑移试验,分别命名为E3D14、E3D18、E3D22,每组重复三次。试件尺寸设计参考规范SL 352—2006 《水工混凝土试验规程》推荐的尺寸和GBT 50082—2009 《普通混凝土长期性能和耐久性能试验方法标准》,ECC基体为150 mm的立方体,钢筋右侧为加载端,且伸出300 mm,左侧为自由端,伸出长度为50 mm,锚固长度为5d,E3D22系列试件简图如图4所示。

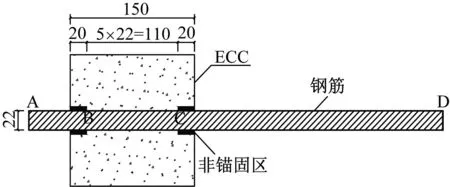
图4 E3D22静力试件设计简图

1.3.2 静力黏结滑移试验加载装置

静力黏结滑移试验采用100 t拉力机进行拉拔试验,试验装置如图5所示,加载速率为0.5 mm/min。钢筋自由端的滑移通过位移计测量,位移计数据由采集箱采集;加载端拉拔力与位移量由拉力机的加载系统采集。加载至试件破坏(系统采集到的黏结力波动变小趋于稳定),停止加载并保存数据。

图5 拉拔试验装置示意图

2 高应变率下钢筋与ECC的黏结滑移试验结果分析

2.1 钢筋-ECC黏结滑移破坏形式

2.1.1 高应变率荷载作用下钢筋-ECC黏结滑移破坏形式

根据高应变率荷载作用下黏结滑移试验结果,总结出试件在高应变率荷载作用下有三种破坏形式：钢筋拔出-ECC劈裂破坏、ECC劈裂破坏和ECC劈裂-钢筋屈曲破坏,破坏形式如图6所示,不同试件破坏形态的试验结果如表6所示。

(a) 钢筋拔出-ECC劈裂破坏

(b) ECC劈裂破坏底面图

(c) ECC试件劈裂破坏侧面图

(d) ECC劈裂-钢筋屈曲破坏

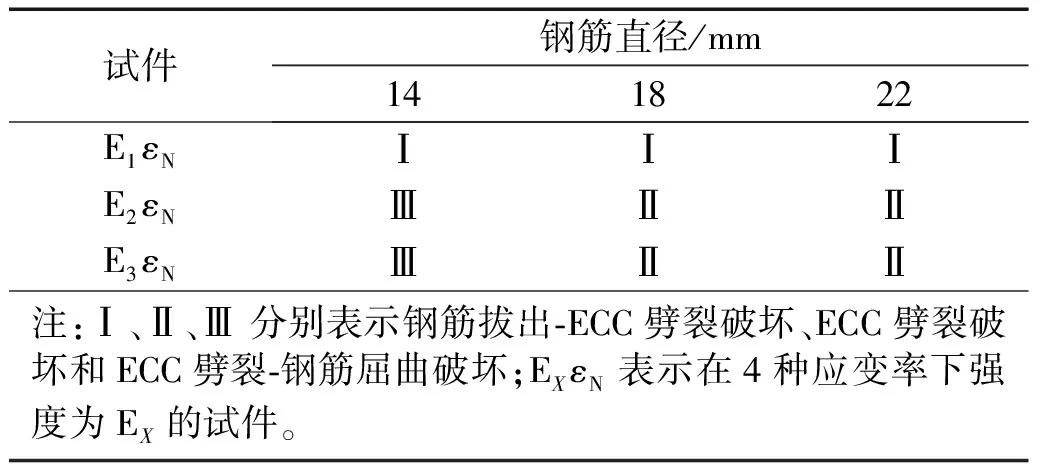
表6 试件破坏形式的试验结果

钢筋拔出-ECC劈裂破坏是指试件中钢筋先被拔出一段距离,ECC发生劈裂破坏,实质是钢筋与ECC黏结锚固被破坏,发生在黏结应力达到峰值应力后的曲线下降段。ECC劈裂破坏是指基体出现弥散状分布式裂纹,混凝土发生了劈拉破坏,发生在黏结滑移曲线的上半段。ECC劈裂-钢筋屈曲破坏主要是指ECC基体劈裂后,钢筋出现屈曲现象从而发生的破坏现象。发生这种破坏的主要原因是钢筋直径较小但ECC强度过高,钢筋的稳定临界力小于其与ECC的黏结力。

2.1.2 静力荷载作用下钢筋-ECC黏结滑移试验破坏形式

在静态黏结滑移试验中,E3强度等级的试件在加载过后均发生钢筋拔出-ECC劈裂破坏,破坏形式如图7所示,与动态试验中钢筋拔出-ECC劈裂的破坏原因相同,均因钢筋与ECC的黏结锚固被破坏。

2.2 高应变率荷载作用下钢筋与ECC的平均黏结滑移关系曲线

钢筋应变在锚固段为不均匀分布,试验将锚固段简化成一个光滑圆柱体模型,认为锚固段的黏结应力是均匀分布的,则平均黏结应力可按照式(1)进行计算

τ=F/πDla

(1)

式中：F为拉拔力;D为钢筋直径;la为钢筋锚固长度。其中拉拔力F=EAεT(t),E为入射杆与透射杆的弹性模量,A是其横截面积,εT(t)为透射应变。

(a) E3D14-02破坏图

(b) E3D18-02破坏图

(c) E3D22-02破坏图

试验时,ECC的压缩量可忽略不计,故可直接将试件两端的位移差作为钢筋的滑移量。钢筋滑移量无法直接获取,根据SHPB试验的一维应力假定[12],结合应力波从而计算出试件两端位移S左、S右,进而求出钢筋滑移量S,见式(2)～(4)

(2)

(3)

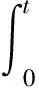
(4)

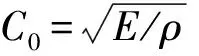
通过以上数据处理方法可以得到高应变率荷载作用下钢筋与ECC的平均黏结滑移关系曲线。

2.3 高应变率荷载作用下黏结滑移性能影响因素分析

试验中考虑了应变率、ECC强度、钢筋直径对钢筋与ECC的黏结滑移关系曲线的影响,并进行了定量分析。

2.3.1 应变率

SHPB试验中所获得的应变率在整个试验中并不恒定,故选用参考相关文献[13]中平台应变率(图8)作为数据分析需要的应变率,平台应变率在体现试验过程中应变率的同时还不会明显小于试件破坏时的瞬时应变率。

图8 应变率-时间曲线

平台应变率不仅与时间有关,还与冲击速度有关,但平台应变率与冲击速度之间的关系还不直观明确,为了进一步研究冲击速度与平台应变率的关系,通过表5的数据将两者关系拟合成曲线,如图9所示。

图9 冲击速度与平台应变率关系

通过图9可以看出,不同冲击速度下的应变率-试件因冲击速度变化幅度不大的原因比较靠拢,无法看出具体变化规律,但可以看出两者呈正比关系,拟合出函数关系式(5)

ε=82v

(5)

式中：ε为平台应变率(s-1);v为冲击速度(m/s)。

为研究应变率对动态极限黏结强度的影响,将不同应变率下相同强度等级相同直径试件的黏结滑移曲线绘制到图10。

(a) 不同应变率下E1D14系列试件的动态黏结滑移曲线

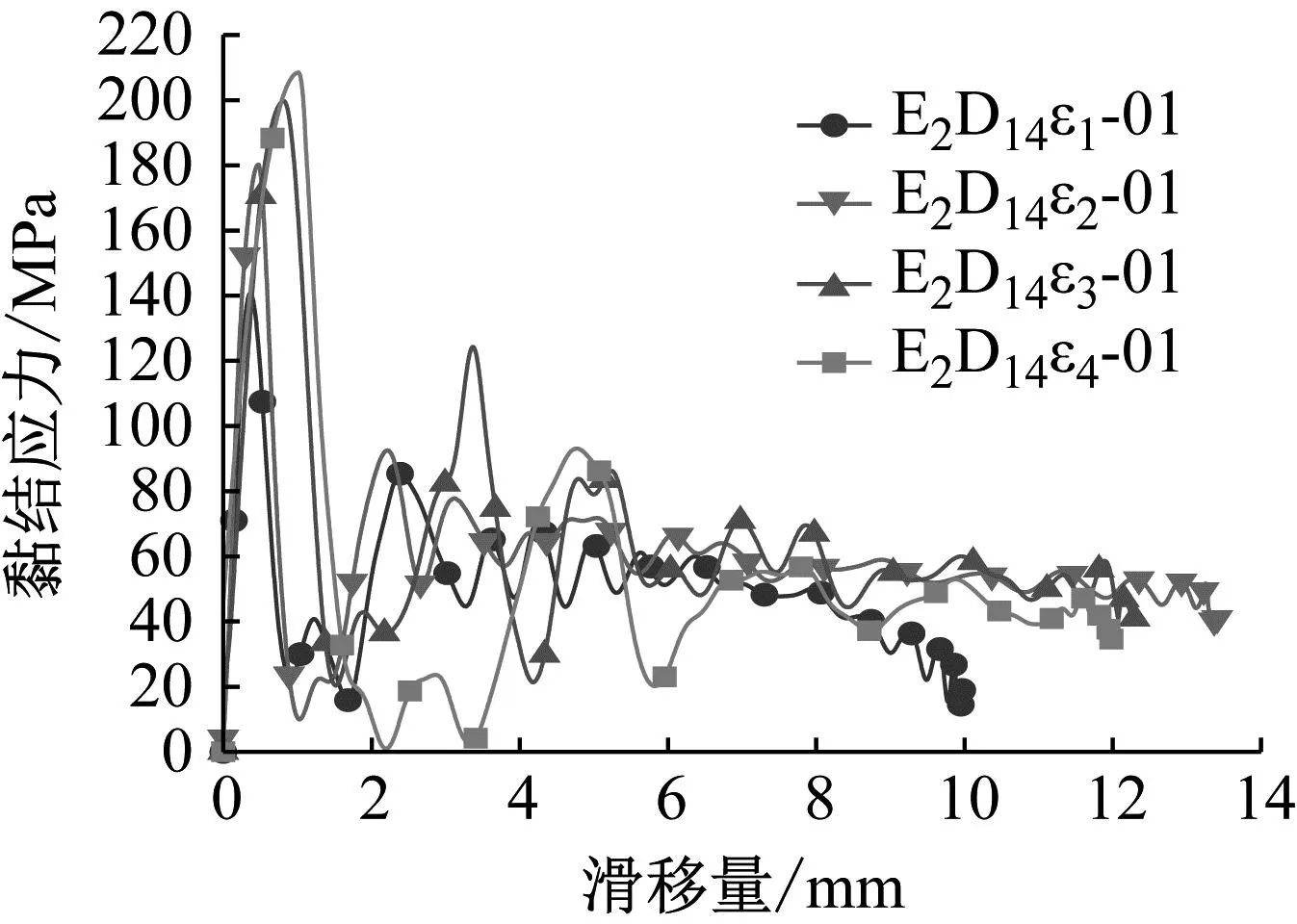
(b) 不同应变率下E2D14系列试件的动态黏结滑移曲线

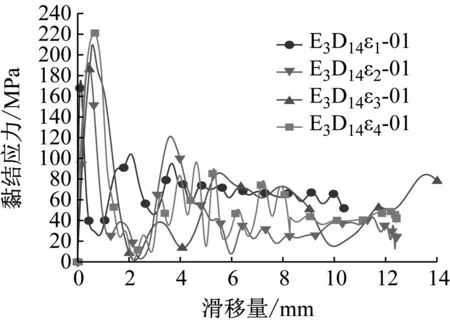
(c) 不同应变率下E3D14系列试件的动态黏结滑移曲线

从图10可以发现,高应变率荷载作用下钢筋-ECC的黏结滑移曲线均由上升段、下降段、残余段这三部分组成。其中上升段是指黏结滑移曲线的第一个上升阶段,曲线基本以线性的方式快速增长到峰值力处,此时峰值处所对应的荷载定义为极限荷载,黏结应力为极限黏结强度,上升段的黏结力主要由机械咬合力和摩擦力组成,机械咬合力为主要部分。下降段指曲线在上升段后的第一个下降段,曲线到达峰值荷载后并未出现峰值水平段,而是直接开始下降,加载端和自由端的滑移量快速增大,钢筋与ECC之间的黏结作用逐渐消失,此时黏结应力由摩擦力和机械咬合力组成。当荷载下降到一定程度,曲线便进入了残余段,可以明显看出动态黏结-滑移曲线呈抖动下降趋势,这是因为在霍普金森动态试验中,钢筋的滑动并不是完全垂直沿着钢筋的轴线方向,导致试件端部与SHPB杆接触不均匀进而造成曲线的抖动,此时黏结应力依旧存在。

根据图10可知,提高应变率可以提高试件的极限黏结强度与滑移量。在四种不同的应变率下,E1D14系列试件极限黏结强度分别提高33.98%、9.65%、5.72%,滑移量分别提高27.16%、54.5%、24.04%;E2D14系列试件极限黏结强度分别提高28.08%、10.81%、4.39%,滑移量分别提高30.54%、72.96%、24.1%;E3D14系列试件极限黏结强度分别提高9.71%、9.11%、5.41%,滑移量分别提高276.44%、33.6%、19%。另外,将黏结滑移曲线上升段中的斜率定义为极限黏结刚度,通过观察图10中曲线上升段可以发现,提高应变率会降低试件的黏结刚度,在相同荷载下试件更容易被破坏。

2.3.2 ECC强度

为研究ECC强度对动态极限黏结强度的影响,将不同强度下相同直径、应变率的三组试件的黏结滑移曲线绘制到图11。

(a) 不同强度等级的D14ε1系列试件的动态黏结滑移曲线

(b) 不同强度等级的D18ε1系列试件的动态黏结滑移曲线

(c) 不同强度等级的D22ε1系列试件的动态黏结滑移曲线

由图11可知,提高ECC强度等级可以提高试件的极限黏结强度,降低滑移量。在E1、E2、E3三种等级强度下,D14ε1系列试件极限黏结强度分别提高26.15%、24.49%,滑移量分别降低25.57%、68.73%;D18ε1系列试件极限黏结强度分别提高21.39%、24.55%,滑移量分别降低26.48%、31.45%;D22ε1系列试件极限黏结强度分别提高12.10%、29.42%,滑移量分别降低40.6%、10.13%。通过图11发现,提高试件的ECC强度等级会提高试件的黏结刚度,说明在相同荷载下试件更不容易被破坏。

2.3.3 钢筋直径

为研究钢筋直径对动态极限黏结强度的影响,将相同应变率下强度等级相同但直径不同的试件的黏结滑移曲线绘制到图12。

(a) 不同钢筋直径的E1ε1系列的动态黏结滑移曲线

(b) 不同钢筋直径的E2ε1系列的动态黏结滑移曲线

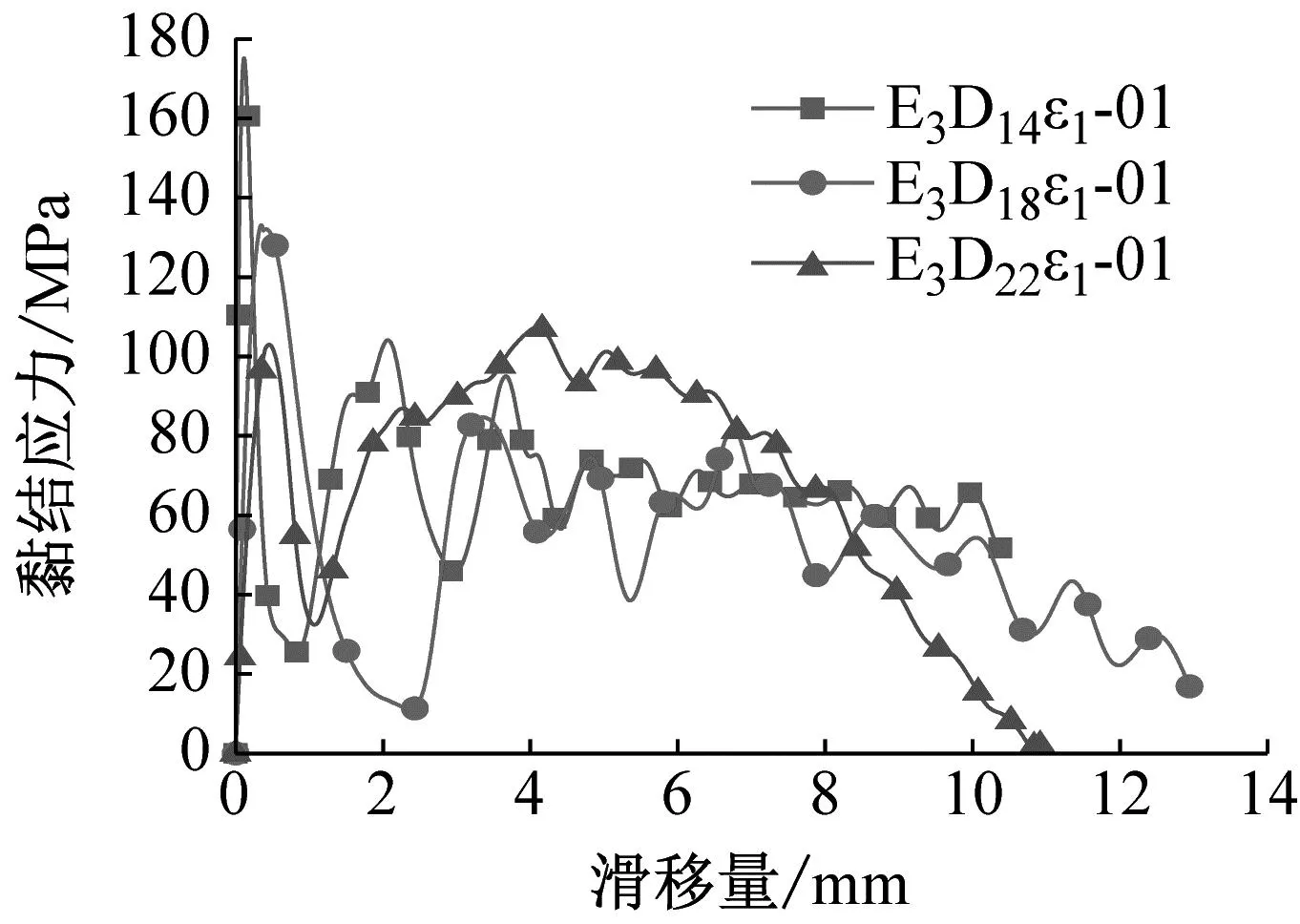
(c) 不同钢筋直径的E3ε1系列的动态黏结滑移曲线

由图12发现,钢筋直径的增加会使试件的极限黏结强度下降,但会使滑移量增长。在D14、D18、D22三种钢筋直径下,E1ε1系列试件极限黏结强度分别降低21.07%、19.42%,滑移量分别提高41.14%、24.99%;E2ε1系列试件极限黏结强度分别降低26.32%、23.24%,滑移量分别提高34.54%、5.45%;E3ε1系列试件极限黏结强度分别降低24.01%、22.61%,滑移量分别提高205.65%、32.38%。通过对图12分析发现,随着钢筋直径的增加,黏结刚度越来越小,说明直径越小试件越不容易破坏,但需注意,这只是表示一定范围内,钢筋直径越小试件越难破坏,并不意味着小直径钢筋一定优于大直径。

2.4 动态黏结强度增强因子分析

动态黏结强度增强因子(DIF)是指动态与静态黏结强度的比值,该比值被广泛的用来量化应变率对混凝土材料的影响。

2.4.1 静力荷载作用下对比试件黏结滑移关系曲线分析

根据静力荷载作用下黏结滑移试验结果得到试件的静力黏结滑移曲线,如图13所示。

(a) E3D14系列

(b) E3D18系列

(c) E3D22系列

由图13可知,ECC-钢筋试件静力荷载作用下的黏结滑移曲线特征与常规混凝土相似,由微滑移阶段、滑移阶段、拔出阶段、下降段和残余段组成。微滑移阶段滑移只发生在加载端且不明显,滑移与黏结力近似成线性关系,此时黏结力主要是化学黏结力。随着拉拔力的增加,ECC-钢筋界面出现从加载端向自由端发展的滑移,曲线进入滑移阶段,此时的黏结力主要包括机械咬合力和摩擦力,机械咬合力为主要部分。黏结力接近峰值时,钢筋与ECC间的滑移量加速增长,出现转折期,此阶段为拔出阶段,黏结力组成与滑移阶段相同。此后曲线进入下降段,黏结应力达到峰值后随后开始下降,滑移持续增加,ECC-钢筋之间的黏结变小,直至钢筋被拔出。通过图13看出在残余阶段曲线仍旧有反复上升下降,说明此阶段依旧存在黏结应力,此时的黏结应力仍为机械咬合力与摩擦力。

2.4.2 动态黏结滑移曲线与静力黏结滑移曲线对比

为了解钢筋-ECC试件在高应变率荷载作用下与静力荷载作用下黏结滑移性能的差异,从动态黏结滑移试验与静态黏结滑移试验各选取了3个试件进行黏结滑移曲线对比分析,如图14所示。

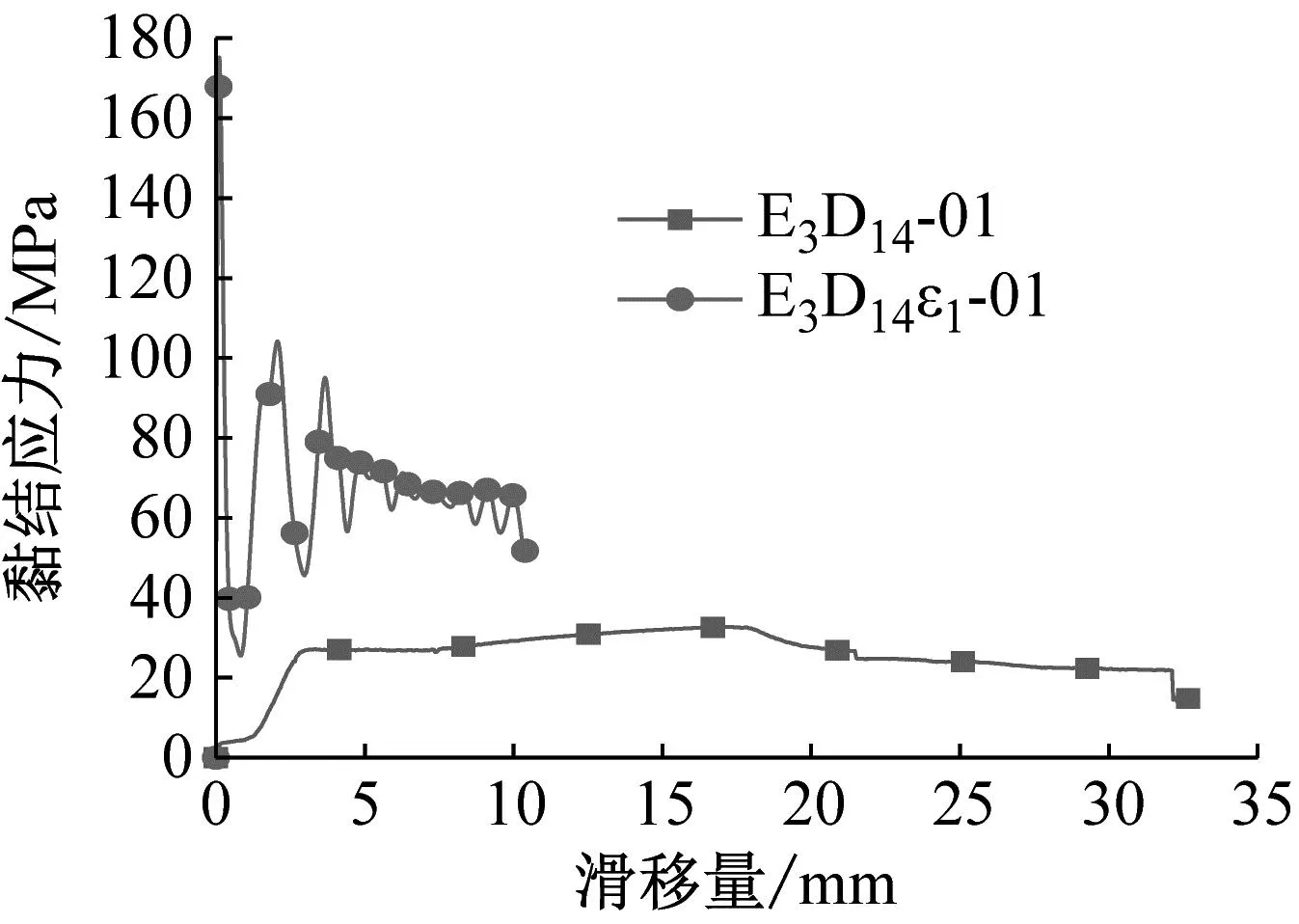
(a) E3D14与E3D14ε1黏结滑移曲线对比

(c) E3D22与E3D22ε1黏结滑移曲线对比

由图14可知,ECC-钢筋的动态与静态黏结滑移曲线都可分为上升段、下降段和残余段,但表现有所不同,动态黏结滑移曲线的上升段可看成一个线性整体,而静态黏结滑移曲线中,上升段表现出胶结段与拔出段,原因是静态黏结滑移试验加载速度慢时间长;同时,动态黏结滑移曲线的峰值与斜率均远大于静态黏结曲线,说明应变率对黏结强度与初始刚度有很强的增强效应;下降段中静态黏结滑移曲线在达到峰值后缓慢下降且有屈服段,而动态黏结坏曲线在峰值后迅速下降,表现出明显的脆性变化;残余段中,静态黏结滑移曲线下降相对光滑,在动态黏结滑移试验中,钢筋在试验过程中出现不完全垂直钢筋轴线方向的滑动从而造成试件端部与SHPB杆接触不均匀,最后在动态黏结滑移曲线残余段中表现成抖动下降。

2.4.3 动态黏结滑移强度增强因子

通过静力拉拔试验时的加载速度0.5 mm/min及式(6)得到准静态黏结滑移试验时的应变率为0.007 s-1,用准静态黏结试验中极限黏结强度平均值τ0.007作为基准参考值,DIF取值方法见式(6)

FDI=τγ/τ0.007

(6)

式中,τγ为应变率为γ时的应变率。

根据公式计算E3强度等级下试件的DIF,并给出了DIF与应变率之间的关系,如图15所示。

图15 E3强度等级下不同直径试件的动态黏结强度增强因子

通过图15可以看出,动态黏结强度增强因子(DIF)的取值范围为5～8。三种钢筋直径试件的DIF都表现出随着应变率增加而增加的线性规律,但可以看出直线的形态有些许区别,这是因为动态黏结强度因子(DIF)受试件材料和试验设备的影响比较大,即使只有钢筋直径不同,DIF也会有区别。

3 高应变率下考虑锚固位置影响的钢筋-ECC动态黏结滑移试验研究

实际应用工程中,黏结应力与相对滑移是随位置不断变化的,本文通过动态黏结滑移试验中钢筋开槽贴应变片的方式获得试验中钢筋在锚固长度内各个测点应变的变化,计算得到各测点的应力和ECC与钢筋相对滑移的分布规律,从而得到不同位置的黏结滑移关系及对应的位置函数。

3.1 钢筋应变沿锚固长度的分布规律

以E1D14ε3-01试件为例,该试件的锚固长度为70 mm,分别在距加载端0、23、46、70 mm(以此作为4个测点,分别为测点1、测点2,以此类推)处贴有应变片,图16给出了各个测点钢筋应变曲线图,根据实测钢筋应变,各个测点的钢筋应力可按公式σ=Eε求得,根据对应的加载时间可以找出每级应变下对应的荷载大小。

图17为各个测点的应力沿锚固长度分布的曲线,从图17中可知：钢筋锚固长度内4个测点的应力随荷载的增加而增加,直至极限荷载;钢筋的应力由加载端向自由端逐步递减,且在加载初期,自由端应力较小,表明此时拉拔力很小,钢筋整体的应力水平较低;钢筋与ECC之间发生滑移,此时两者间的胶结力消失,加载端应力开始大幅度增加,自由端的应力出现小幅度增加,在达到极限荷载后,钢筋应力开始减少。

图16 E1D14ε3-01试件钢筋锚固长度内各测点的钢筋应变曲线

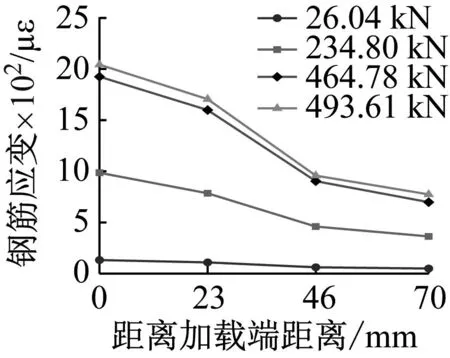
(a) 极限荷载之前

(b) 极限荷载之后

3.2 黏结应力沿锚固长度的分布规律

常用的黏结应力使用方法如式(1)所示,求得的是平均黏结应力,不能直接得到钢筋与ECC之间的黏结应力,但可以通过钢筋沿锚固长度内各个测点的应变分布间接测得,洪小健提出的矩阵方程组的方法[14]可直接计算出每级荷载作用下各个测点的黏结应力,利用该方法获得的黏结应力沿锚固长度的变化曲线如图18所示。

从图18可以看出：黏结应力在锚固长度范围的分布并不均匀。在极限荷载前,每个测点处的黏结应力随着荷载的增加而增加;自由端的应力远小于加载端的应力;自由端的黏结应力随着荷载的增加发展迅速,并越来越接近加载端;当荷载快达到极限荷载时,加载端和自由端的黏结应力发展已经趋于稳定,开始同步增加;当荷载达到峰值之后,各个测点的黏结应力随着荷载的降低呈下降趋势。

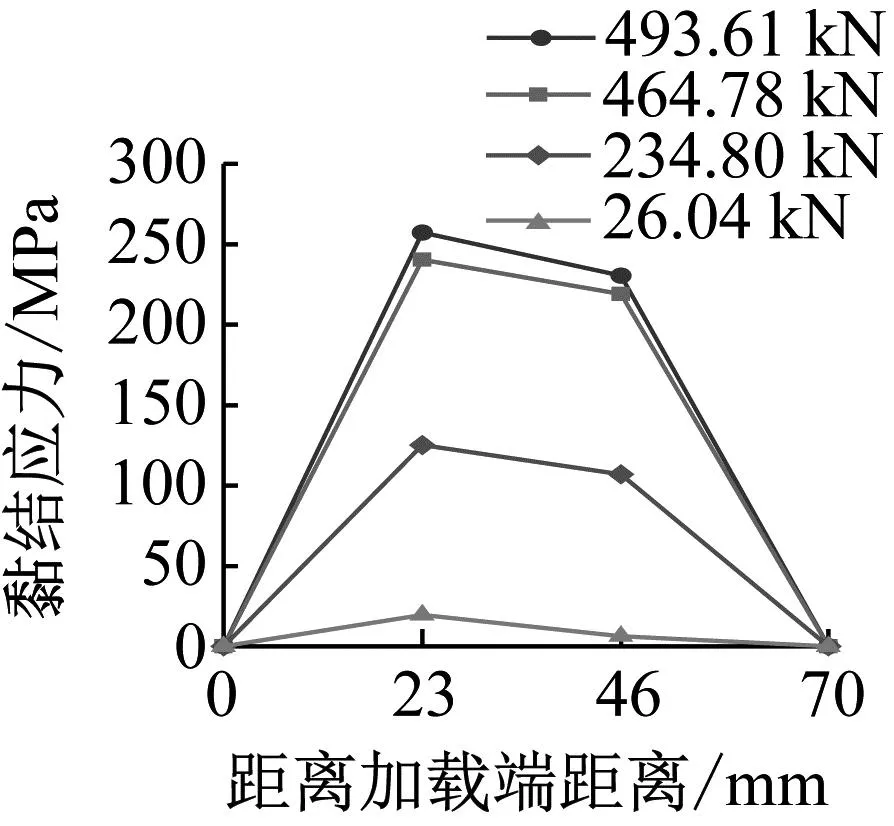
(a) 极限荷载之前

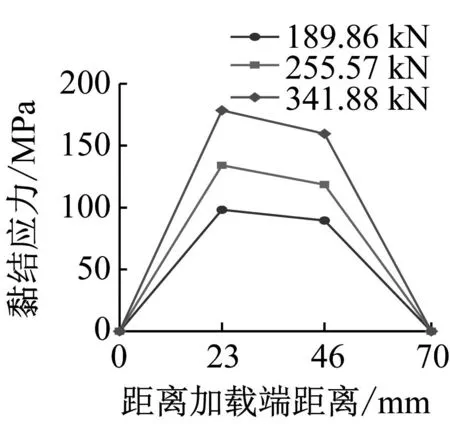
(b) 极限荷载之后

3.3 钢筋-ECC相对滑移量沿锚固长度的分布规律

锚固长度范围内钢筋与ECC之间的相对滑移量可以通过两者变形的差值计算得到,任意荷载等级下钢筋-ECC之间的相对滑移量都可根据式(7)计算得出。

钢筋在相邻测点间的变形为Δlsi=εsih(εsi为钢筋各测点的应变,h为各测点间距),根据静力平衡可得钢筋周围ECC的平均应力σci和平均应变εci,ECC变形为Δlci=εcih,则依据钢筋和ECC各个微段的变形可计算出钢筋与ECC之间相对滑移Sz。由于在荷载作用时,ECC的横截面上黏结应力的分布并不均匀,故本文引入ECC的不均匀变形系数γc=0.75考虑这一因素的影响[15],综上可由式(7)求得距离自由端x处的钢筋与ECC的相对滑移量Sx

(7)

式中：n=x/h;Sz为黏结滑移曲线中每级荷载下测得的钢筋与ECC相对滑移。

图19给出了E1D14ε3-01试件在每级荷载作用下,钢筋与ECC的锚固长度范围相对滑移量曲线。由图19可知,加载之初,黏结力主要为胶结力,此时钢筋与ECC在整个锚固长度范围的相对滑移量都比较小;继续加载,胶结力随之消失,钢筋与ECC之间的滑移量开始增加;随着荷载的继续增加直至极限荷载,滑移量增加到最大;因为动态黏结滑移试验的加载在一瞬间完成,所以在整个试验过程中自由端的滑移都滞后于加载端;极限荷载之后,滑移量随着荷载的减小而增加。

3.4 黏结滑移关系沿锚固长度的变化

通过本文计算得到沿锚固长度的各个测点位置处的黏结应力与钢筋-ECC之间的相对滑移量,可以拟合出不同位置处的黏结滑移关系曲线,具体的拟合公式见多项式(8)

τ=a+bs+cs2+ds3

(8)

式中：s为滑移量,mm;τ为黏结应力,MPa;a、b、c、d为拟合系数。

(a) 极限荷载之前

(b) 极限荷载之后

表7给出了测点2和测点3通过式(8)得到的拟合结果。

表7 示例试件不同测点黏结应力与相对滑移量关系拟合结果

图20为E1D14ε3-01试件在不同锚固位置处的黏结滑移试验值与拟合曲线的对比,由图可知：不同锚固位置的动态黏结滑移关系并不相同,且会发生变化。即钢筋与ECC之间的黏结应力除与滑移量有关以外,还受到锚固位置x的影响。因此考虑锚固位置在黏结滑移关系中的影响是有必要的。

图20 不同位置处的黏结滑移曲线

3.5 黏结-滑移位置函数

根据式(8)可以计算出各级滑移量下不同锚固位置所对应的黏结应力。表8给出E1D14ε3-01试件在滑移量分别为0.70 mm、0.75 mm、0.80 mm时,黏结应力τ沿锚固长度分布的数据。图21是E1D14ε3-01试件在各级滑移量下经过标准化计算后的黏结应力τ沿锚固长度的分布规律曲线。由图21可知,滑移量发生变化时对试件的黏结应力基本没有影响,其大小只与锚固位置有关。

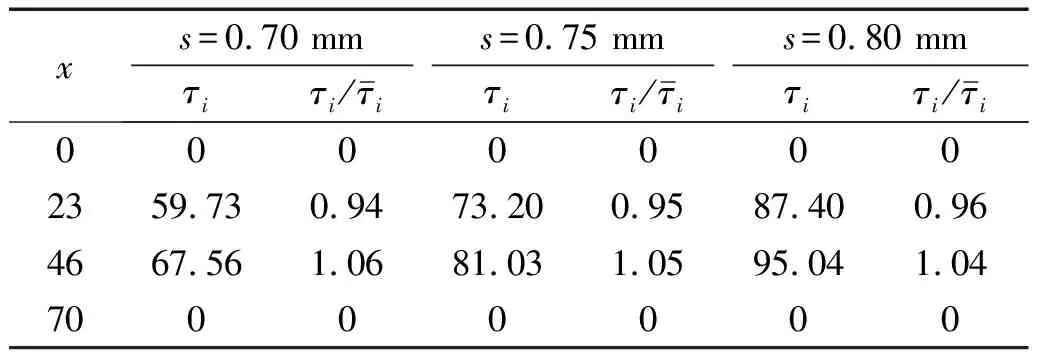
表8 试件E1D14ε3-01在每级滑移量下沿锚固长度方向的各测点处的黏结应力

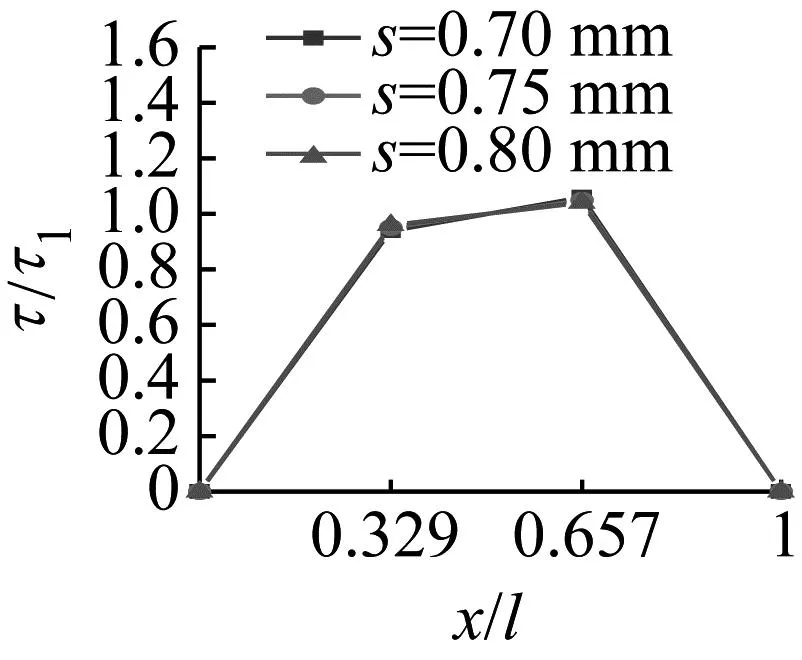
图21 不同滑移量下的标准化黏结滑移关系曲线

由于不同滑移时位置函数的纵坐标基本相差不大,计算各点的黏结应力取平均值并进行拟合,得到钢筋与ECC的黏结滑移锚固位置函数ψ(x),见式(9)

(9)

4 高应变率下考虑位置影响的黏结滑移本构关系

根据试验结果拟合得到基准黏结滑移本构,在此基础上采用位置函数进行修正,得到高应变率下考虑位置影响的钢筋与ECC的动态黏结滑移本构,为有限元分析提供理论基础。

4.1 高应变率下钢筋与ECC的基准黏结滑移本构拟合

文中将试验获得的黏结滑移曲线与国内外普遍应用的改进BPE模型、CMR模型以及连续曲线模型进行了拟合对比,选取最佳模型进行系数修正,将所有试件的黏结滑移曲线结果与提到的几种本构模型进行拟合,文中给出部分试件的拟合结果,如图22所示。

由图22可知,改进BPE模型的拟合结果在上升段拟合较好,但结果较为保守;在下降段,改进PPE模型拟合结果呈直线形式,而实际试验结果下降段为曲线形式,下降段模拟效果不理想。大多数结构在计算时仅考虑试用阶段,所以CMR模型只提出了上升段的本构公式,CMR模型的模拟结果与实际试验值之间的偏差较大,CMR模型的模拟效果较差。通过连续曲线模型的模拟结果可以看出,连续曲线模型在上升段的模拟结果与实际试验值有一定偏差,且均高于实际试验值;下降段模拟值与实际试验值偏离过大且出现分段情况。但通过图22可以看出,实际试验值与模拟结果的曲线变化趋势相似。

(a) E2D22ε1-02

(b) E3D22ε4-02

(c) E1D18ε1-01

(d) E3D14ε2-01

因连续曲线模型与实际试验值的曲线相似度最高,故选取连续曲线的关系式作为黏结滑移本构关系的初始方程,见式(10)。结合试验结果并通过最小二乘法回归得到系数a、b,其中a为常数0.7,b为与S0、Su相关的一个多项式,系数b的关系拟合图如图23所示,详情见式(11)。通过相关系数a、b对连续曲线模型进行修正,提出了包含上升段与下降段的两曲线模型,关系式如式(12)所示。系数b的多项式拟合如图23所示。

(10)

式中：τ0、S0为峰值黏结应力及相对应的滑移量;τu、Su为残余黏结应力及相对应的滑移量。

(11)

图23 系数b的多项式拟合

(12)

将试验结果代入修正后的平均黏结滑移本构关系式进行拟合,对试验值与拟合结果进行对比分析,部分试件拟合及试验值的对比分析图如图24所示。由图24可知,平均黏结滑移本构的拟合值与实际试验结果的吻合度较好。

(a) E2D22ε1-02

(b) E3D22ε4-02

(c) E1D18ε1-01

(d) E3D14ε2-01

4.2 高应变率下考虑位置影响的钢筋与ECC的黏结滑移本构关系

由现有的关于黏结滑移性能的相关研究可知黏结滑移本构关系是随锚固位置不断变化的,为了表征钢筋-ECC的黏结滑移关系与锚固位置的相关性,可以通过已获得的基本黏结滑移本构的基础上与位置函数的乘积来表述高应变率荷载作用下不同位置处钢筋-ECC的黏结滑移本构关系,具体见式(13)

τ(s,x)=φ(s)ψ(x)

(13)

5 结 论

本文通过SHPB装置及设计的附属装置,考虑应变率(953.94 s-1、1 015.95 s-1、1 081.31 s-1、1 165.86 s-1)、ECC强度(49.1 MPa、57.7 MPa、68.6 MPa)、钢筋直径(14 mm、18 mm、22 mm)等影响因素,共设计制作108个试件,进行动态黏结滑移试验,得出以下结论：

(1) 给出了高应变率荷载作用下钢筋-ECC黏结滑移的三种破坏模式。

(2) 获得了高应变率荷载作用下钢筋-ECC的黏结滑移曲线,发现极限黏结强度随应变率的增加、ECC强度的提高、钢筋直径的减小而增大。进一步,通过与静态黏结滑移试验结果进行对比分析,得到了动态极限强度增强因子DIF。

(3) 得到了考虑不同锚固位置影响的黏结应力-滑移关系曲线,对试件的黏结应力曲线进行归一化处理得到了黏结滑移关系位置函数。

(4) 基于试验结果拟合出基准黏结滑移本构,在此基础上采用位置函数进行修正,得到高应变率下考虑位置影响的钢筋与ECC的动态黏结滑移本构关系。