基于CEEMD-MPE-IMPROVEDWTD的爆炸振动信号噪声抑制方法

童晓玲, 曾斐宇, 江 轲, 梁 磊

(武汉理工大学 机电工程学院, 武汉 430070)

爆破振动是爆炸后炸药的部分能量以弹性波的形式向外传播,使岩体发生振动的现象。爆破振动分析是研究爆破振动损伤控制技术的重要基础之一[1]。在防护工程试验中,为了准确定位爆炸源,需要分析爆炸产生的振动信号。但由于爆破现场环境的复杂性和现场设备的误差,爆破测量信号中含有大量的噪声成分,给信号分析带来了困难。为了确定采集到信号的特征,获得真实的信号,需要对被测信号进行降噪处理。

爆破振动信号是典型的非平稳、随机信号,可用经验模态分解类算法进行去噪处理。khaldi等[2]采用EMD(empirical mode decomposition)算法对语音信号进行去噪。Kopsinis等[3]设计了一种基于经验模态分解并结合频率分析的新去噪方案,该方案在原始信号能量水平较低时,去噪效果较好。但EMD分解会出现明显的端点效应和模态混叠,需要对算法进行改进。Chen等[4]利用WT(wavelet transform)和EEMD(ensemble empirical mode decomposition)对电磁声信号去噪,发现EEMD的适应性更强,优于WT。虽然EEMD分解可以改善模态混叠现象,但去噪效果仍不理想。CEEMD(complementary ensemble empirical mode decomposition)算法是EMD的一种改进算法,既保留了EMD处理非平稳信号的优点,又能有效克服EMD的模态混叠问题。但CEEMD去噪方法会直接丢弃高频IMF分量,直接重构剩余的低频IMF(intrinsic mode function)分量,从而导致高频[5]分量高频噪声抑制不完全或有效信号丢失。

小波算法同样适用于处理非平稳信号[6-11],Jiang等[12]提出了小波模量最大算法,通过试验证明小波变换是一种有效的信号去噪算法。Zhang等[13]将小波阈值去噪方法应用于爆破振动信号的预处理,并对四种去噪阈值进行比较。小波阈值函数分为硬阈值函数和软阈值函数。传统的硬阈值和软阈值去噪效果都存在不足。硬阈值会在某些点产生不连续,导致较大的均方误差和波形振荡,而软阈值容易造成高频信息的部分丢失。改进的小波阈值函数可以在一定程度上消除前两个阈值函数的缺陷。面对单独使用模态分解方法和小波方法所遇到的问题,两种方法可以结合起来抑制信号[14-17]的噪声。与单一CEEMD方法和分离小波变换方法相比,该组合方法对微震信号去噪效果更佳。

本文提出了基于MPE的CEEMD和小波阈值相结合的噪声抑制方法,对爆破振动信号进行去噪处理。首先对被测信号进行CEEMD分解,得到各阶IMF分量;其次,得到各阶IMF的MPE值。根据MPE阈值确定高频分量和低频分量。最后,利用改进的WTD对高频分量进行处理,同未去噪的IMF分量进行重构,完成信号去噪,并应用于震源定位的预处理。

1 CEEMD-MPE-WTD算法

1.1 CEEMD原理

CEEMD算法是EMD的一种改进算法,它既保留了EMD在处理非平稳信号方面的优点,又能有效克服EMD的模态混叠问题。CEEMD的主要步骤如下：

(1) 向原始信号中加入n组正负成对的白噪声,生成2n组信号。

(2) 对2n组信号分别进行EMD分解,得到2n组IMF分量cij。其中i表示添加辅助噪声的第i个信号,j表示对该信号进行EMD分解得到的第j个IMF分量。

(3) 对2n组IMF分量对应尺度取平均,得到CEEMD的对应分解结果

(1)

1.2 多尺度排列熵原理

多尺度排列熵(multiscale permutation entropy, MPE)是计算时间信号经过不同尺度粗粒度运算后的排列熵,可以分析信号的随机性和复杂性。步骤如下：

(1) 对时间序列X={x(i),i=1,2,…,N}进行粗粒化处理得到粗粒化后的序列

(2)

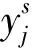
(3)

式中：m为嵌入维数;τ为延迟因子。

(4)

(5)

(4) 对尺度因子为s的序列的排列熵进行计算并归一化处理

(6)

通过MPE方法分析CEEMD分解得到的各阶IMF的复杂性,判断MPE值大于0.6的IMF为高频分量,MPE值小于0.6的为低频分量[18]。

1.3 小波阈值原理

小波阈值算法广泛应用于信号去噪和图像去噪中。其原理是对信号进行小波分解,得到一系列小波系数,判断大于阈值的小波系数为有用信号,而确定小于阈值的小波系数为噪声,可以去除[19],从而达到抑制噪声的目的。小波阈值算法的具体步骤如下：

(1) 对信号进行小波分解。在分解时,需要选择合适的小波基和分解层数。常用的小波基有dB小波和sym小波。经过多次试验选择了sym8小波。选择3层作为分解层的数量。

(2) 阈值处理,选择固定阈值。

(3) 阈值函数分为硬阈值函数和软阈值函数。但软硬阈值法本身也存在一些缺陷。硬阈值函数在阈值处不连续,对于每一层细节分量,经过阈值处理后得到的小波系数都会产生额外的振荡。软阈值函数是连续的,但经过阈值处理后的小波系数与小波系数之间存在恒定的偏差。为了提高小波阈值去噪(wavelet threshold denoising, WTD)效果,采用软硬阈值折衷函数作为阈值函数。

软硬阈值折衷函数的表达式是

(7)

式中：ω为阈值处理前的小波系数;ωthr为阈值处理后的小波系数;thr为小波阈值;α为调整参数,0≤α≤1。

(4) 信号重构。重构阈值处理后的近似分量和细节分量,得到小波阈值去噪后的信号。

改进的小波阈值函数,如图1所示。

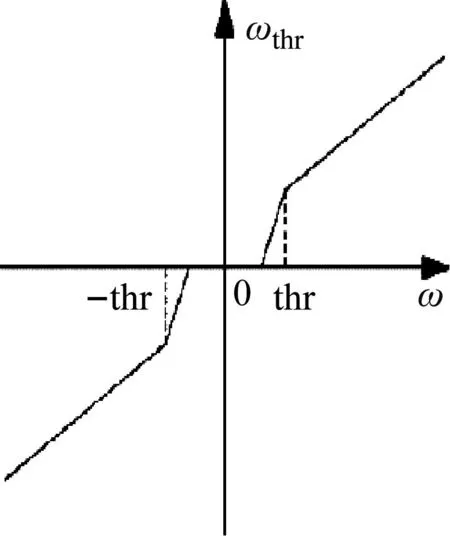
图1 改进的小波阈值函数

1.4 信号去噪算法

本文提出的去噪算法是将CEEMD、MPE和改进的WTD算法相结合。算法流程图如图2所示。噪声抑制方法的实现步骤如下：

(1) 对被测信号进行CEEMD分解,得到各阶IMF。

(2) 计算IMF的MPE值。当IMF的MPE大于0.6时,可以认为是一个有噪声的高频分量,需要进行去噪处理。当IMF的MPE小于0.6时,可以认为是低频分量。

(3) 采用改进的WTD算法对高频分量进行去噪,并与低频分量重构。

2 仿真信号分析

由于由正弦和余弦信号组成的叠加信号与爆破振动信号[20]具有相似的特性,我们利用叠加信号来验证所选方法的性能。仿真信号可以表示为

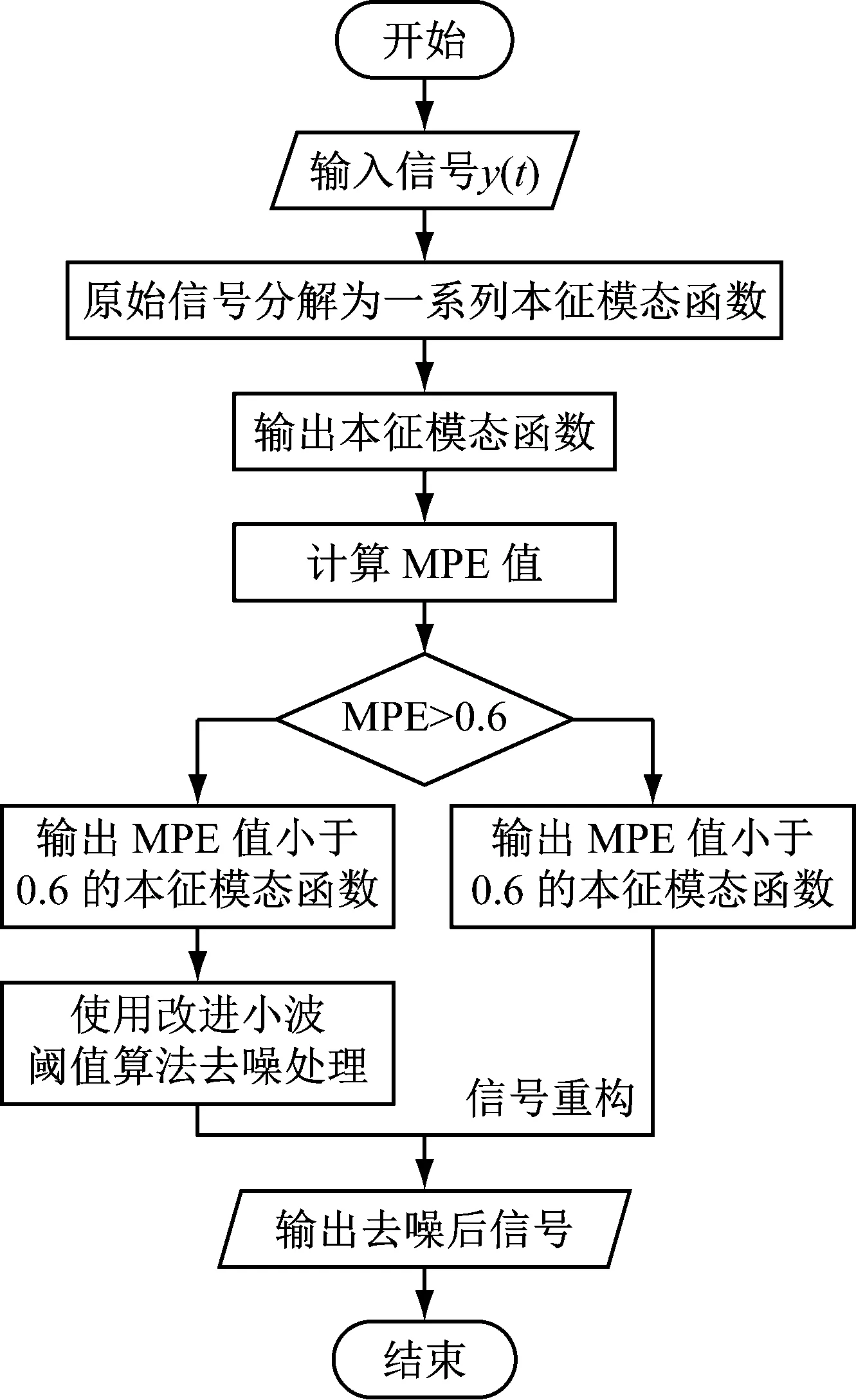
图2 基于CEEMD、MPE和改进WTD的噪声抑制流程图

(8)

式中,y4为高斯白噪声。

分别使用EEMD-MPE方法、CEEMD-MPE方法、CEEMD-MPE-WTD方法和CEEMD-MPE-IMPROVED WTD对模拟信号y(t)进行去噪处理,采用信噪比(signal-to-noise ratio, SNR)、均方根误差(root mean square error, RMSE)和皮尔逊相关系数(Pearson correlation coefficient, PCC)作为抑制噪声的指标,处理结果如表1所示。

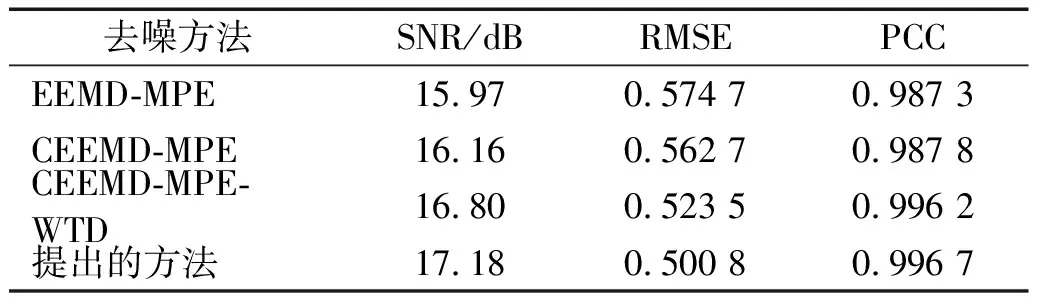
表1 四种不同方法的噪声抑制效果比较

由表1可知,CEEMD-MPE-IMPROVED WTD处理得到的信号信噪比最高,均方根误差最小。通过计算四种去噪方法下纯净信号和去噪信号的PCC值,发现该方法去噪方法的PCC值最接近1,表明该方法中的去噪信号与纯信号最相关,能够最有效地保留原始信号的有效信息。

结果表明,CEEMD-MPE-IMPROVED WTD算法效果最佳,为后续对实测隧道爆破振动信号的降噪处理提供了理论依据。

3 工程实例

CEEMD-MPE-IMPROVED WTD算法研究是基于江苏省南京市的隧道爆炸试验。土地为相对平坦的黄土层,含一定程度的砂土,相对干燥坚硬,表面有少量砾石。

在实际爆炸试验中,以隧道为爆炸主体,在隧道口放置炸药进行爆炸,在隧道外铺设光缆,采用分布式光纤声传感系统(distributed acoustic sensing, DAS)结合光缆采集爆炸振动信号。DAS是一种最先进的光纤声学检测技术,它使用光纤作为传感器来检测振动信号。通过检测光纤中瑞利后向散射的变化,几乎可以在光纤上的任何点检测振动信息[21]。现场平面测试图如图3所示。现场试验的场地存在约为1 m的垂直高度差,测试场地长度约为100 m,宽度约为50 m。本次爆炸试验中使用的DAS系统的空间分辨率为1 m,采样频率为20 000 Hz,最大测量长度为20 km。

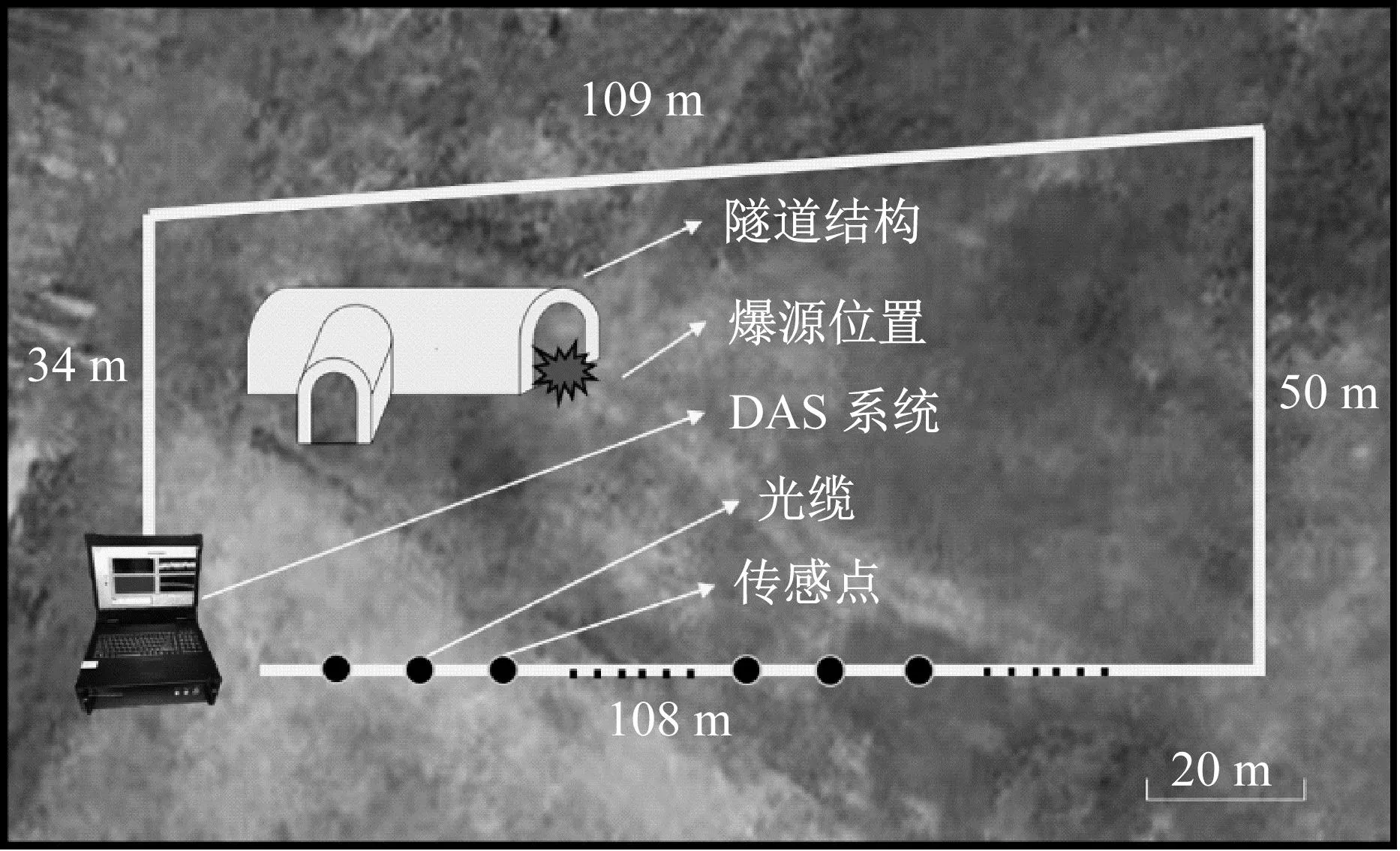
图3 测试系统整体示意图

DAS系统采集的震源时空数据可以组成矩阵。假设有L个传感节点,传感节点个数由DAS系统的空间分辨率和光纤长度决定,DAS系统采集时间序列长度为N=fs×t;其中t为时间,t=1 s;fs为采样率,fs=20 kHz。由此可得N行L列的DAS信号矩阵

(9)

光缆响应图即为原始数据X所绘制瀑布图,其中横轴代表光缆的位置信息,单位为m。纵轴代表时间信息,单位为s。光缆响应图的颜色代表信号的强度,颜色越深,代表该该位置该时刻的光相位变化越明显。其中某一位置的信号波形如图4所示。光缆响应图如图5所示。

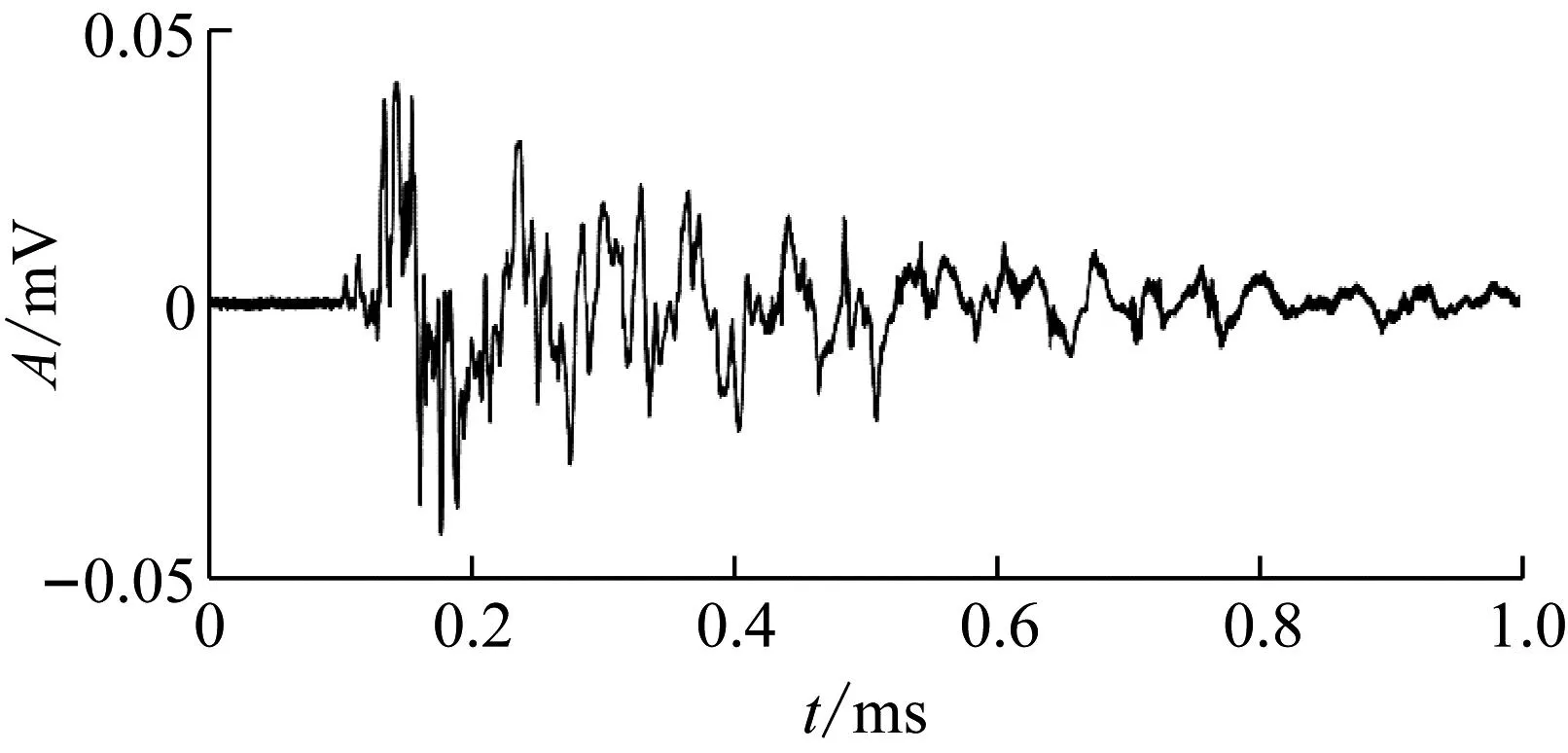
图4 爆破振动信号

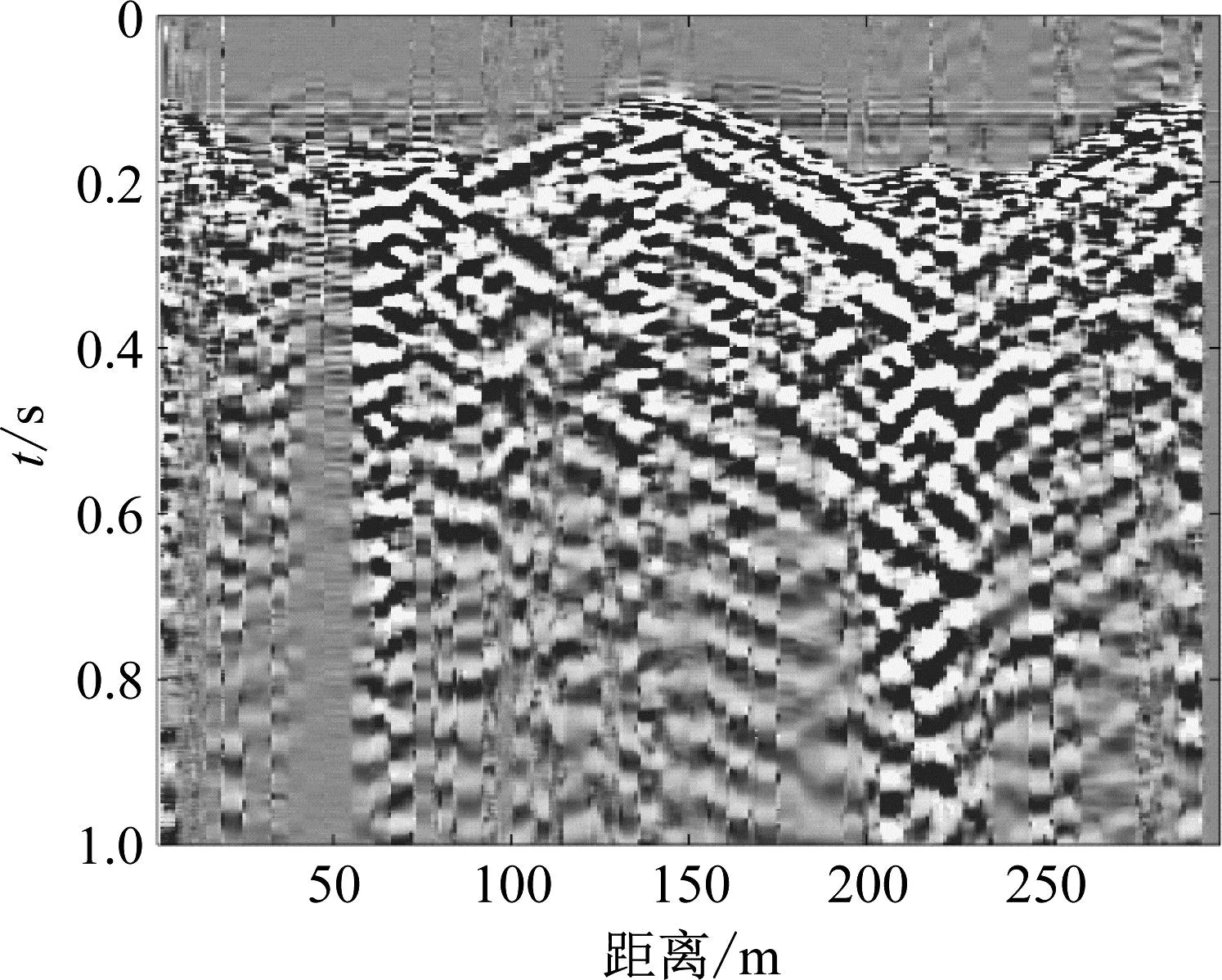
图5 光缆响应图

在对采集到的爆炸信号进行去噪时,首先对一个信号进行CEEMD分解,得到各阶IMF,并绘制其频谱图,结果如图6所示,我们可以看到通过测量信号的CEEMD分解获得的各阶IMF分量及其频谱。可以看出,一阶和二阶IMF包含频率约3 000 Hz的设备共振噪声、环境噪声和有用信息。如果直接丢弃一阶和二阶IMF分量,信号中的有用信息将丢失,信号将失真。因此,为了获得真实信号,有必要在尽可能抑制噪声分量的同时,将有用信息保留在高阶IMF分量中。

在信号通过CEEMD方法分解得到各阶IMF后,我们使用MPE方法来判断各阶IMF的类型。IMF1～IMF2的MPE值大于0.6,这被视为噪声分量,需要使用改进的WTD进行去噪;IMF3～IMF11的MPE值小于0.6,将其视为信号分量,并在去噪后用噪声分量重构。

为了说明改进WTD对高频分量中噪声分量的抑制效果,将CEEMD分解得到的IMF1分量与经过改进小波阈值处理后的IMF1分量进行了比较,绘制了它们的波形和频谱图,如图7所示。

如图7所示,经过改进的小波阈值去噪后,时域波形的噪声分量显著减少,频谱IMF1的噪声分量的幅度从0.248降低到0.147,表明IMF1经过此方法处理后确实可以抑制噪声分量。然而,信号的有用成分也存在一定程度的降低。

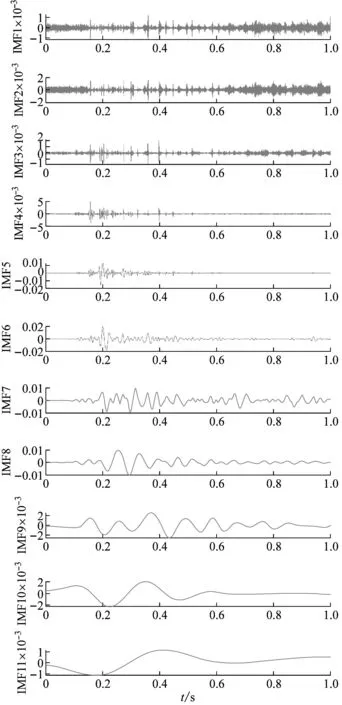
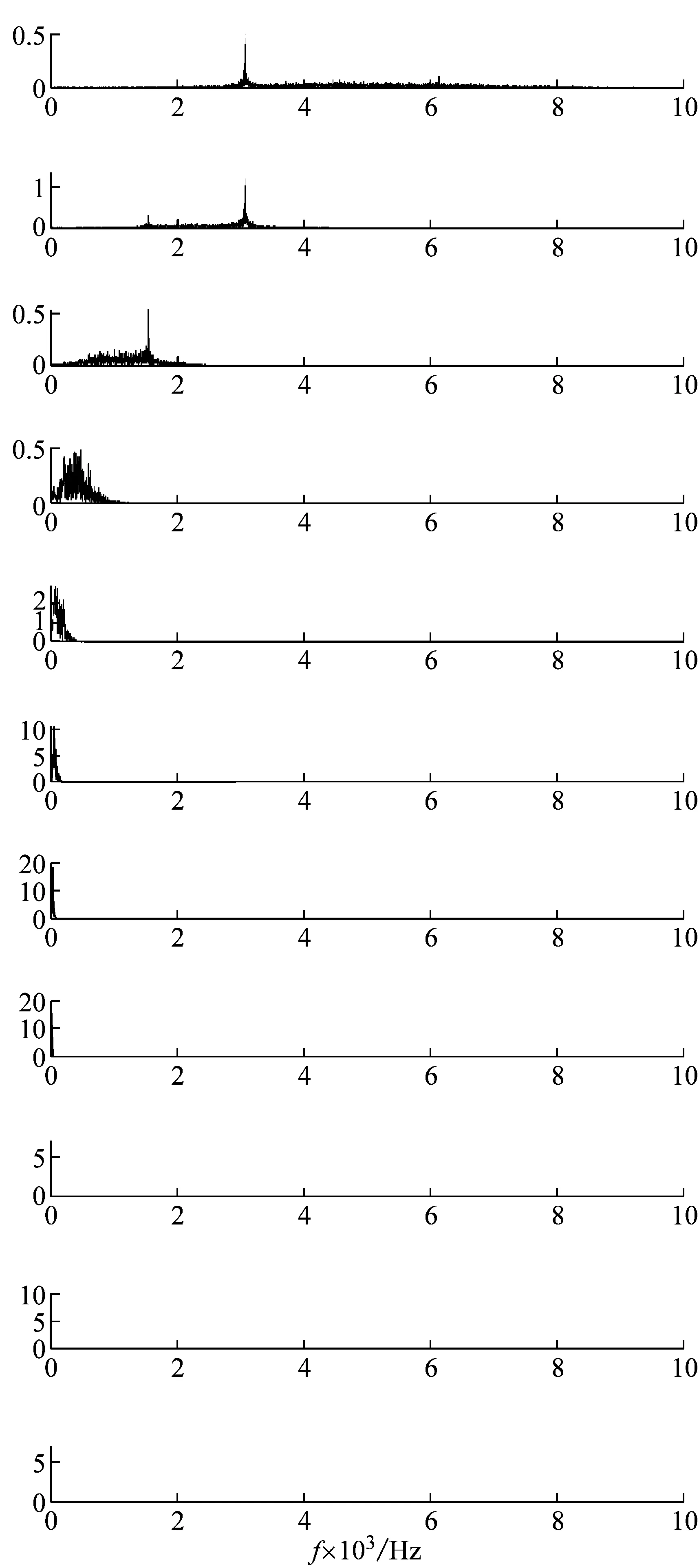
图6 CEEMD分解结果及其对应的谱

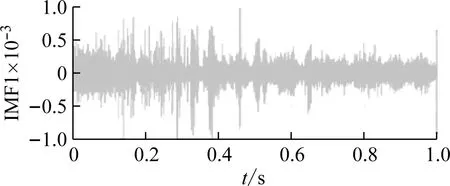
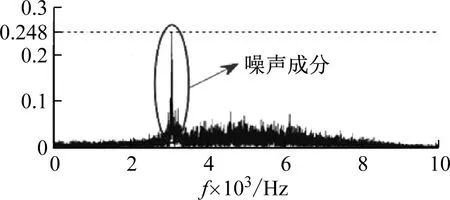
(a) CEEMD分解得到IMF1

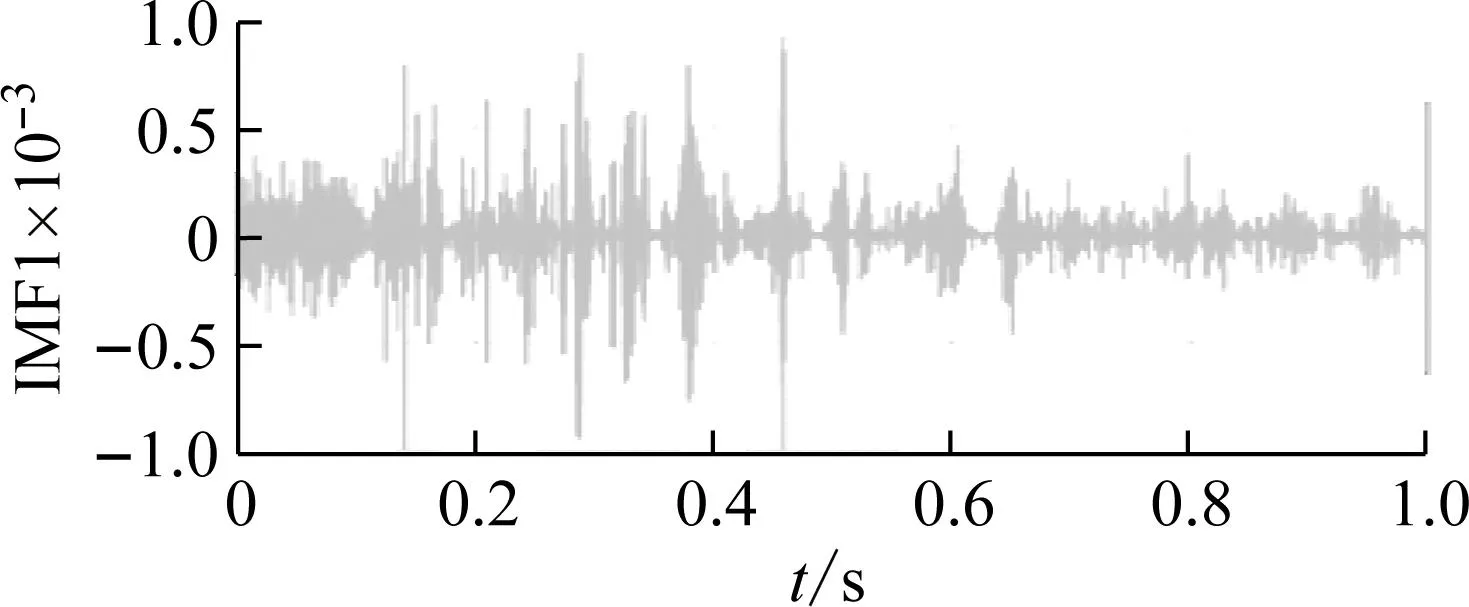
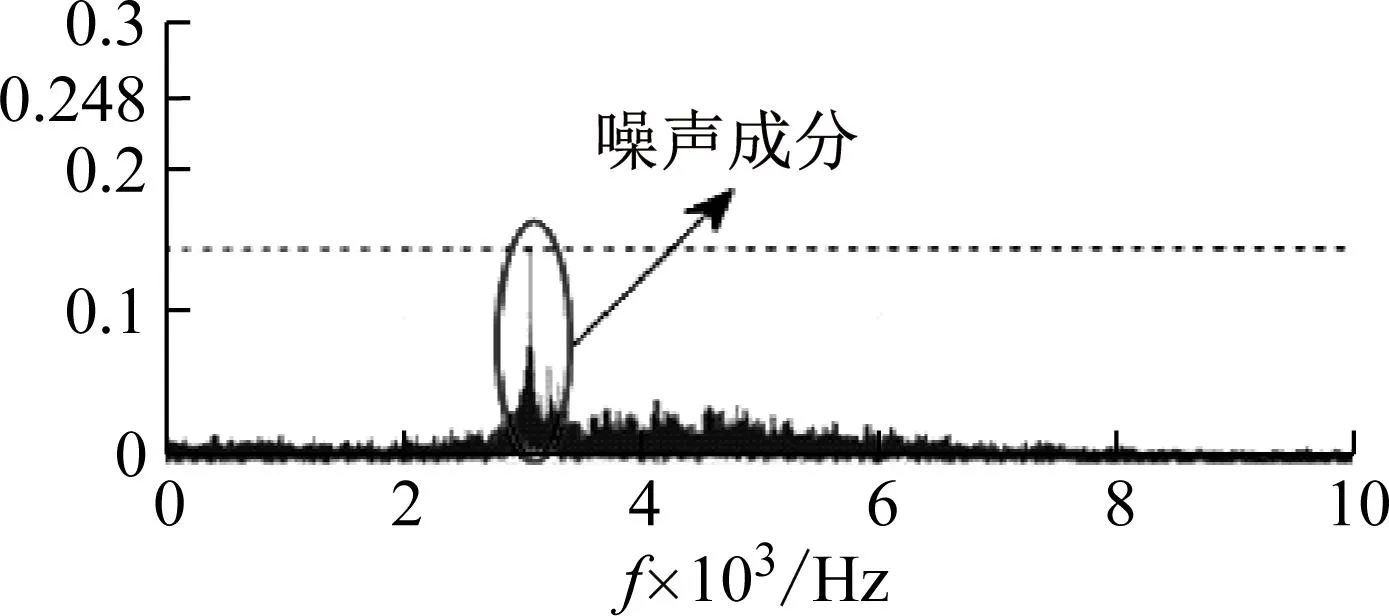
(b) 改进小波阈值处理得到的IMF1

为了分析该去噪算法中有效成分的损失程度。我们将信噪比为25 dB的高斯白噪声添加到采集的信号中,并分别通过EEMD-MPE、CEEMD-MPE、CEEMD-MPE-WTD和CEEMD-MPE-IMPROVED WTD算法进行去噪。每个信号的波形图和AOK时频分析图如图8所示。X是主频能量,Y是主频。

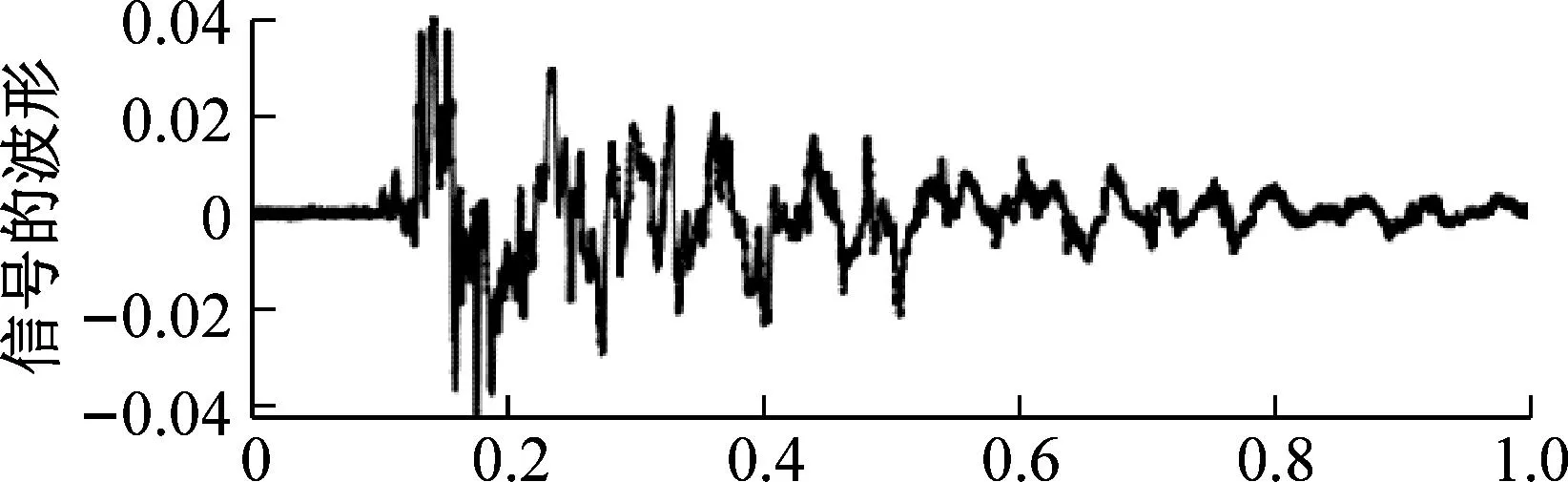
(a) 原始信号

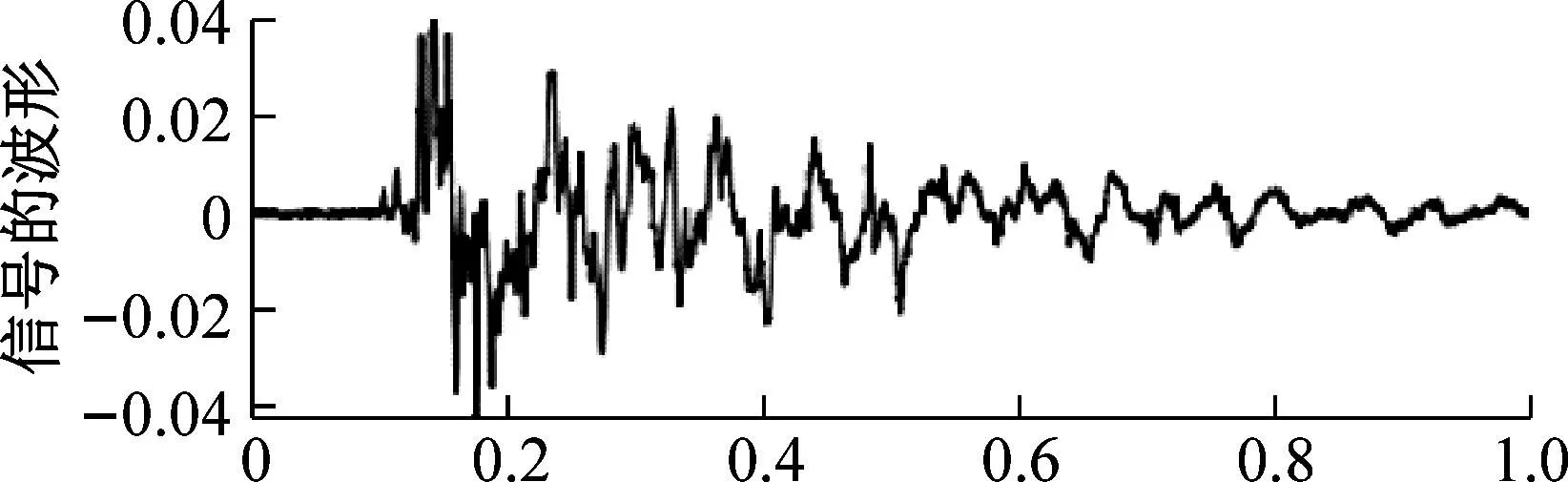
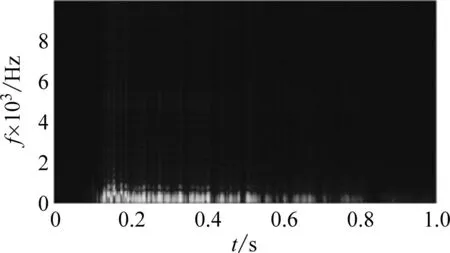
(b) EEMD-MPE 方法

(c) CEEMD-MPE 方法

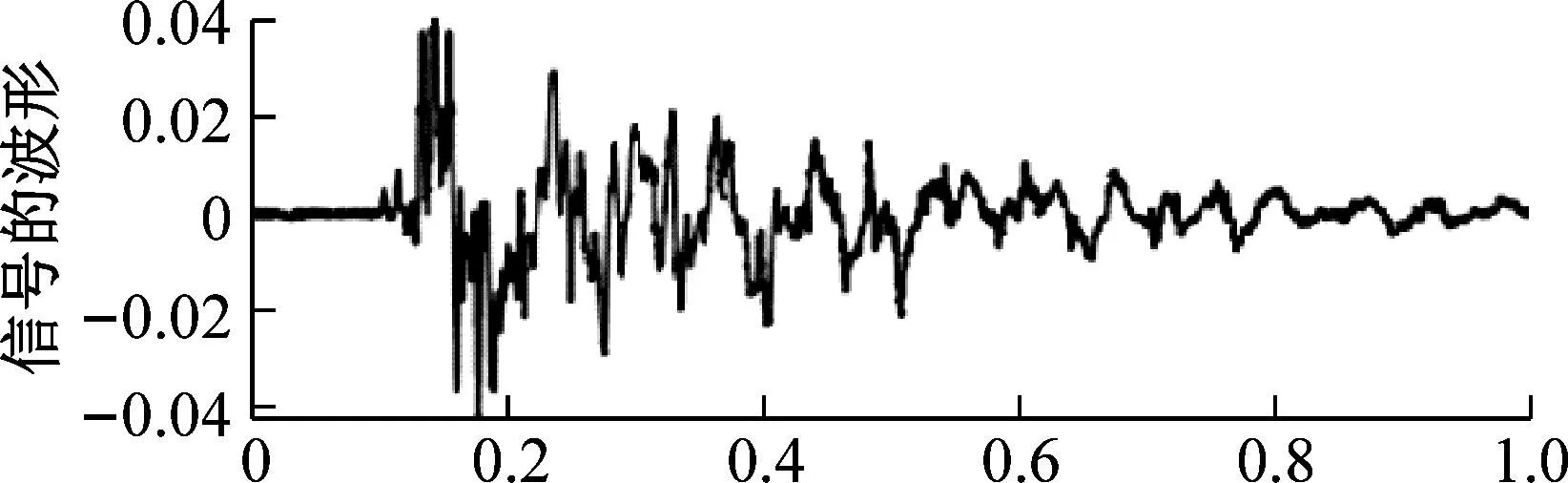
(d) CEEMD-MPE-WTD 方法

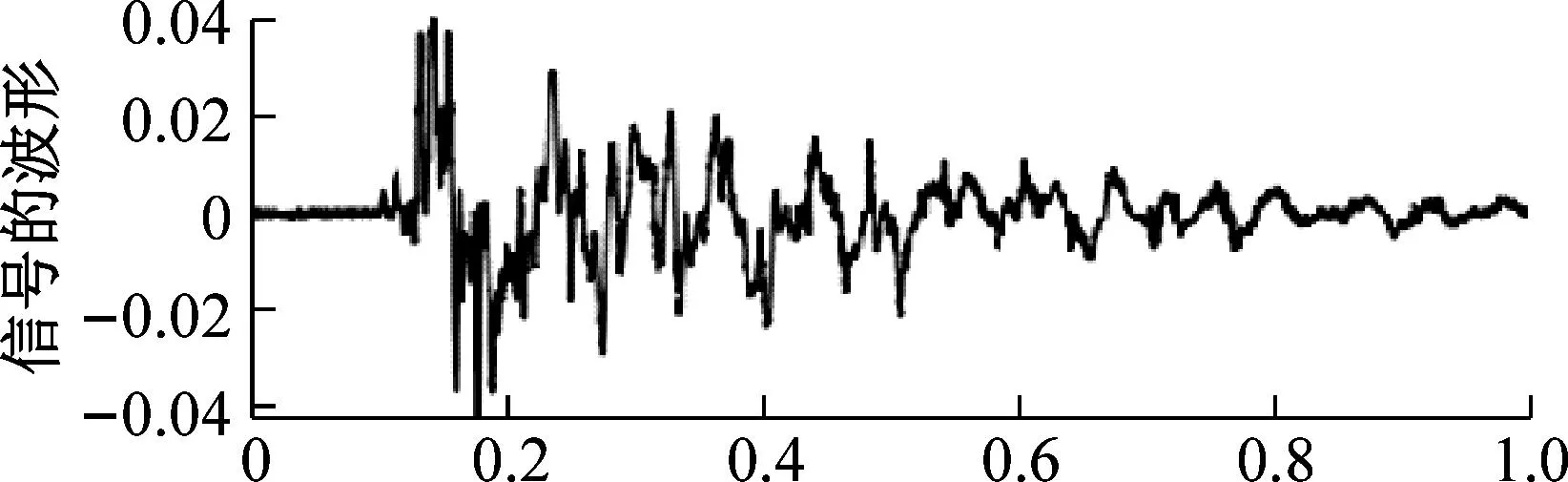
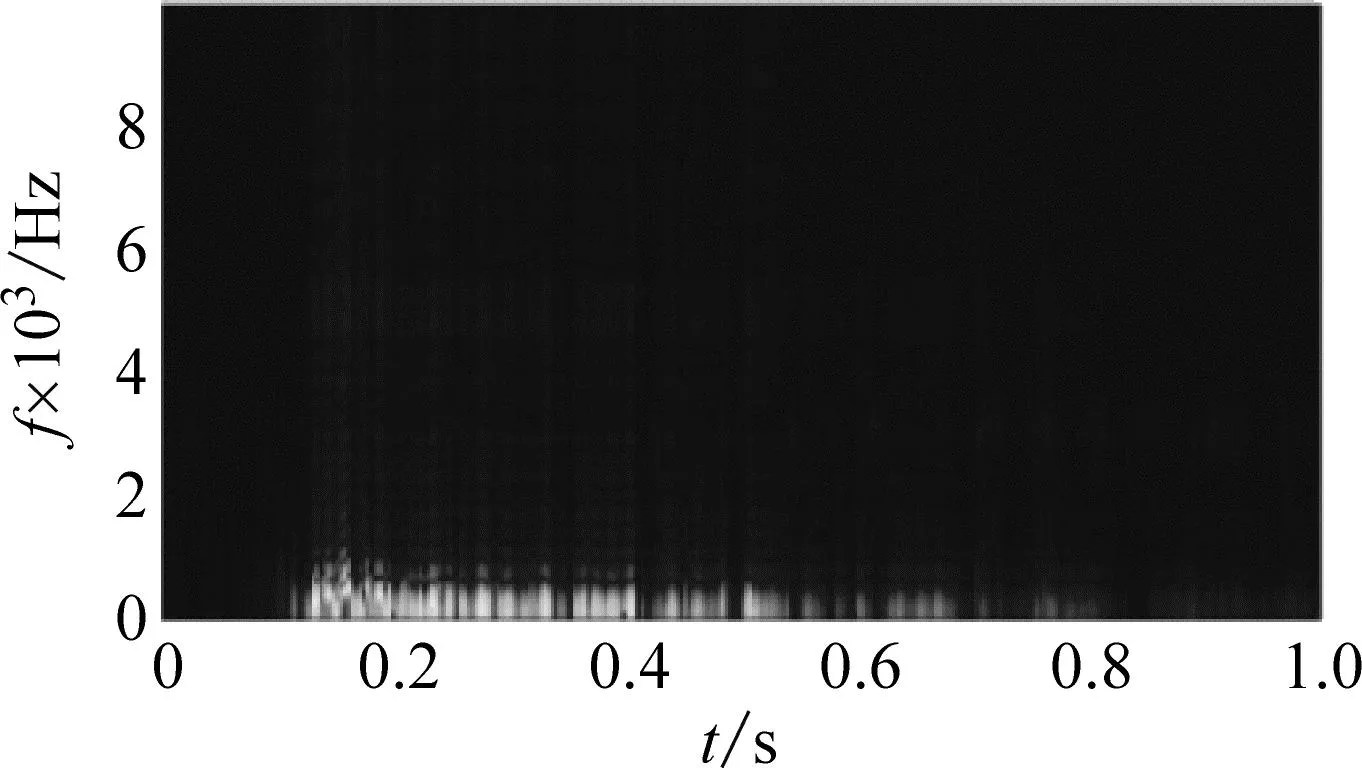
(e) CEEMD-MPE-IMPROVED WTD方法

图8显示了原始信号和通过各种方法去噪的信号的波形图和频谱图。信号的采样时间为1 s。从图8(a)中的频谱图可以看出,原始信号的主频率能量为64.760 4,并且在3 053 Hz的频率处存在峰值能量为3.84的噪声分量。

从信号波形可以看出,CEEMD-MPE方法由于直接丢弃高频IMF分量,3 053 Hz频率处的噪声分量消失,信号波形最平滑。似乎CEEMD-MPE方法后的信号去噪效果最好。但将原始信号的主频能量与通过各种方法去噪的信号的主频能量进行比较时,如表2所示。本文提出方法的主频能量仅减少了0.000 2,其他方法获得的主频能量损失ΔX=0.000 5～0.053 8,与本文提出方法相比能量损耗相差很多倍。且使用本文提出的去噪方法,3 053 Hz处信号噪声分量的能量从3.84降低到1.53。由此可以判断出,CEEMD-MPE-IMPROVED WTD算法相比于其他算法,不仅能很好地抑制信号中的噪声,而且在很大程度上保留了信号的有效成分。

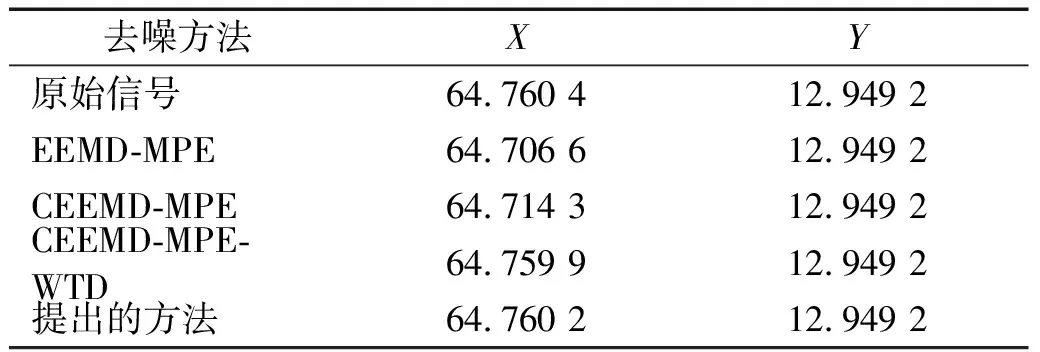
表2 各方法的信号主频能量X和主频Y的结果比较

为了进一步证明CEEMD-MPE-IMPROVED WTD算法的优越性,用上述各种方法对信号进行去噪处理,并计算信号的SNR和RMSE。

表3为EEMD-MPE、CEEMD-MPE、CEEMD-MPE-WTD和CEEMD-MPE-IMPROVED WTD算法的噪声抑制结果指标。CEEMD-MPE-IMPROVED WTD算法相比于其他方法信噪比明显提高,均方根误差显著降低。证明了噪声抑制方法的合理性和有效性。

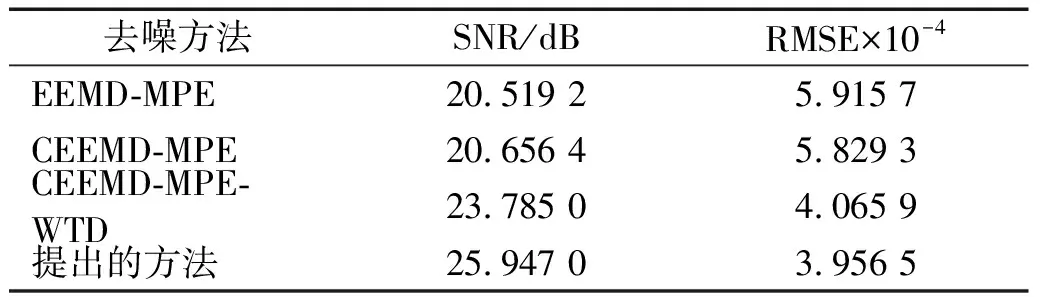
表3 四种方法的噪声抑制结果比较

为了进一步验证该方法的适用性,我们随机选择了采集的40个爆炸信号,添加25 dB的高斯白噪声,采用该方法应用于这些数据的去噪,求取SNR和RMSE并作图。

图9显示了采用四种不同方法对随机选择的40个振动信号噪声抑制后的SNR值。从图9可以看出,CEEMD-MPE-IMPROVED WTD算法获得的SNR值明显高于其他算法。图10显示了采用四种不同方法对随机选择的40个振动信号噪声抑制后的RMSE值,CEEMD-MPE-IMPROVED WTD算法得到的RMSE值最低,证明了本文提出算法的优势。

图9 四种方法的信噪比值的折线图

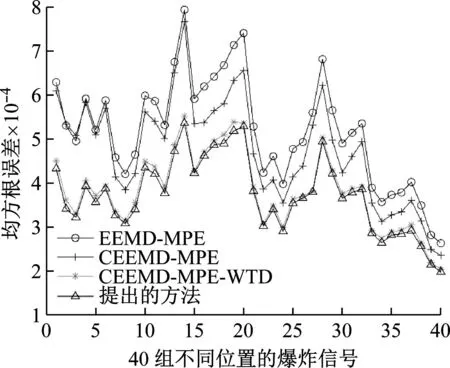
图10 四种方法的均方根误差值的折线图

为了验证本文提出的去噪方法在震源定位中的作用,分别利用去噪前后的数据进行震源定位前的信号到时提取。已知DAS系统和光缆起始通道在(0,0)坐标处,真实震源位置为(60,25)。

采用Geiger定位方法,首选确定一个目标函数,利用接收点到估计震源和到真实震源的走时差最小确定,并采用优化算法使目标函数值最小[22]。

目标函数如下所示

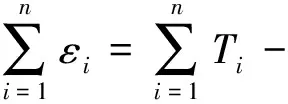
(10)

式中：Ti为光缆第i个传感点接收到振动信号的时刻,即信号到达时间,利用赤池信息准则(Akaike information criterion, AIC)算法求得;t0为炸药爆炸时刻;v为振动波在地下的传播速度;(xi,yi,zi)为光缆第i个传感点的坐标;(x,y,z)为假定震源位置;n为光缆上传感点的个数,且n=300。

由于现场试验的场地并非完全水平,存在约为1 m的垂直高度差。但是现场测试时,测试场地长度约为100 m,宽度约为50 m,由于高度引起的误差可忽略。所以本稿件中目标函数可简化为

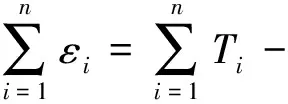
(11)

利用遗传算法优化得到使误差值ε最小的假定震源坐标(x0,y0),认为遗传算法优化得到的震源坐标(x0,y0)即为真实震源位置。分别利用去噪前后信号进行10次定位,得到光缆的实际响应图与定位结果图。

如图11所示为原始信号的到时提取结果以及震源定位结果图。 图11(a)中每个通道上的点代表算法捕捉的每个信号的起始时间。已知震源真实坐标为(60,25),由于噪声成分的干扰使得地震波初至时间判断存在较大误差,据此计算得到的震源位置与真实震源位置差距较大,定位结果如图11(b)所示。

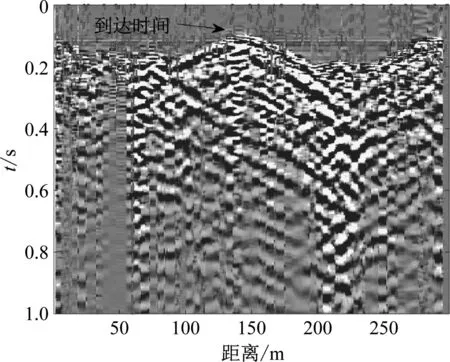
(a) 原始信号的光缆响应图

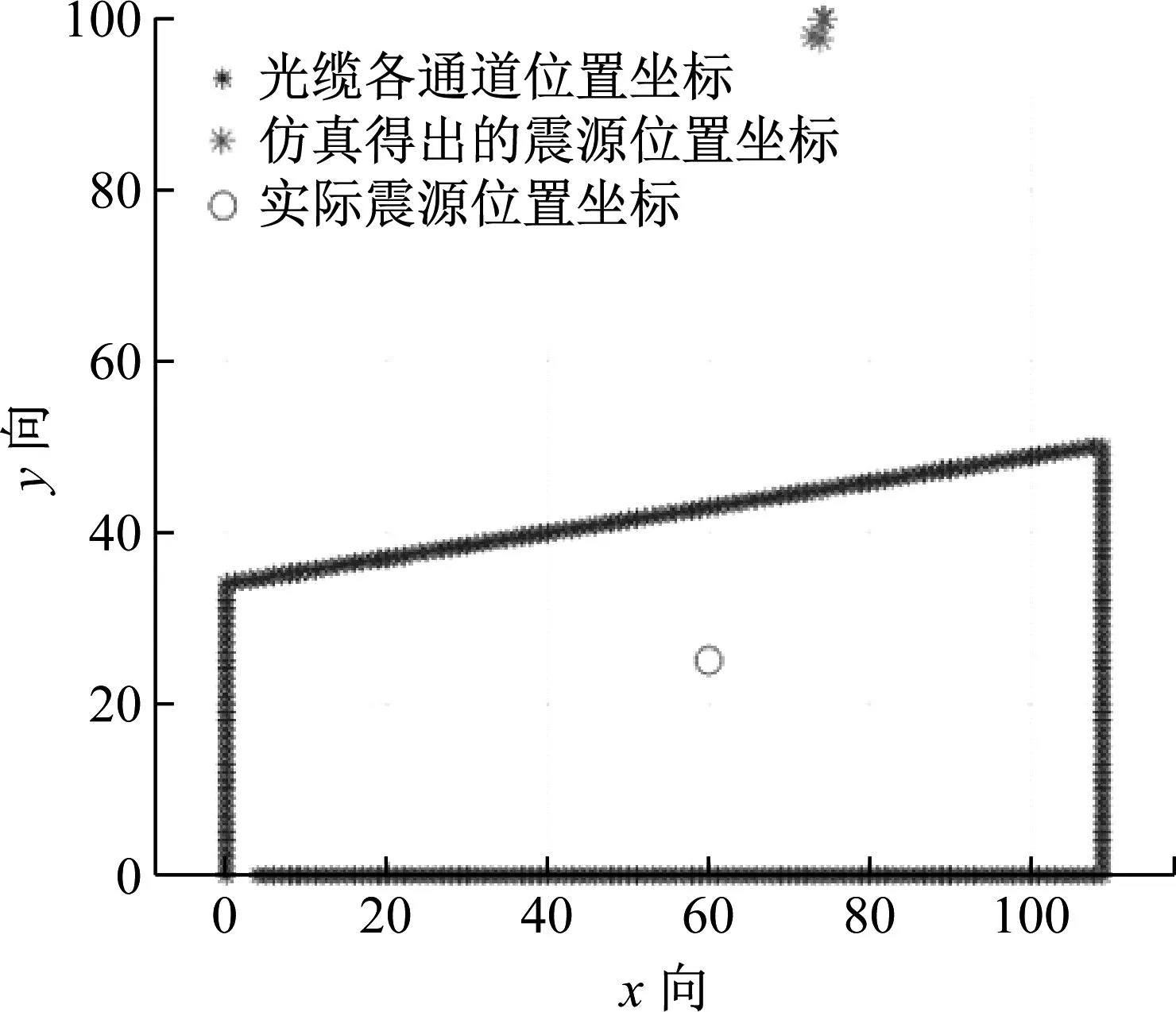
(b) 原始信号的定位结果图

利用去噪后的信号重复定位过程,如图12所示,到时提取的时间能较为准确的反映地震波到达的起始时间,通过去噪后得到的到时计算的震源位置为(64,27),与震源真实位置(60,25)误差为5 m左右。

(a) 去噪后信号的光缆响应图

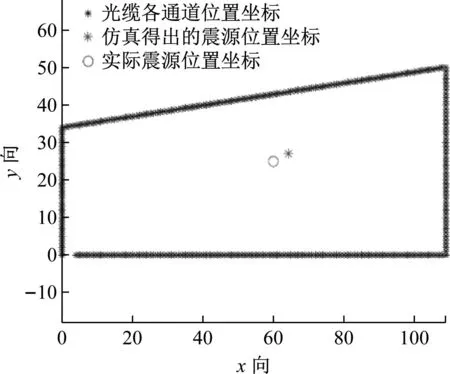
(b) 去噪后信号的定位结果图

为了进一步确认论文提出方法优越性,分别采用原始数据、EEMD-MPE、CEEMD-MPE、CEEMD-MPE-WTD以及本文提出算法去噪后,利用相同的定位算法求出定位结果以及定位误差,并绘制表格如表4所示。

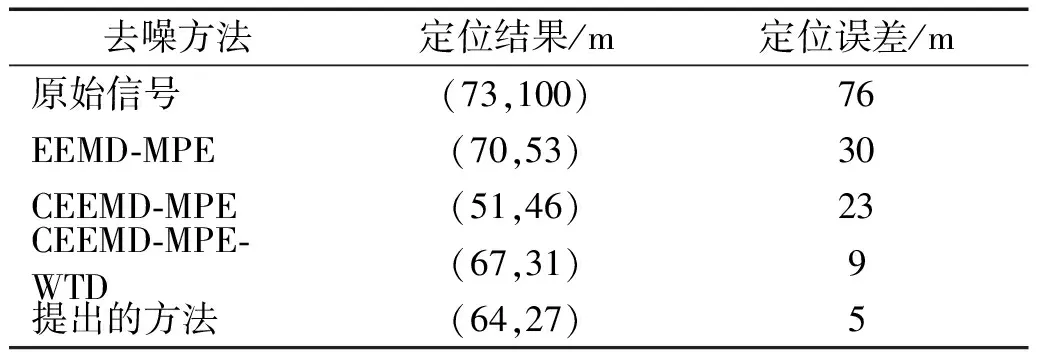
表4 不同算法的定位结果对比

根据定位结果可以得出结论,该去噪算法对爆炸振动信号有较好的去噪效果,可用于震源定位前对信号的预处理。

4 结 论

本文提出了一种基于互补集成经验模态分解(CEEMD)、多尺度置换熵(MPE)和改进小波阈值去噪(WTD)的融合降噪方法对爆炸振动信号进行降噪处理。结论如下：

(1) CEEMD,MPE,以及改进WTD的融合算法在处理隧道的爆破振动信号时效果较好,可有效地去除隧道爆破振动信号的高频噪声成分。

(2) 基于AOK时频分析技术,分析CEEMD-MPE-IMPROVED WTD算法得到的信号波形及主频能量可知,该算法在有效去除噪声成分的同时,由于保留了高频IMF分量,信号的主成分几乎没有损失。为后续分析爆源位置及炸药威力奠定了基础。

(3) 采用EEMD-MPE、CEEMD-MPE、CEEMD-MPE-WTD和CEEMD-MPE-IMPROVED WTD算法分别处理爆炸振动信号时,CEEMD-MPE-IMPROVED WTD算法处理后的信号的去噪效果最优。对随机40个信号进行重复试验,得出相同结论。验证了该算法的有效性和适用性,适合用于隧道爆炸振动信号的去噪处理。

(4) 将CEEMD-MPE-IMPROVED WTD算法处理后的信号用于震源定位应用中,定位误差不超过5 m,远优于原始信号定位结果,说明该方法适合用于爆炸信号定位前的信号预处理过程。