基于CEL法的破损边界附近气泡动力学特性研究
张 啸, 崔 杰, 李明远, 秦孜凯
(江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)
现代战争中,船舶在受到攻击破损后仍具备一定的抗沉性和破舱稳性,在战场上仍具有作战能力,当其受到二次打击时,可丧失战斗能力。Cui等[1-2]基于控制变量法,利用高速摄影技术和电火花气泡试验装置研究了背空气面的水下爆炸问题,发现一定的距离参数和破口参数,气泡呈现中部凹陷并产生对射流的特殊气泡运动特征。贺铭等[3]通过电火花试验验证了欧拉有限元法解决双层结构附近水下爆炸问题的有效性,总结了不同破口参数、不同起爆位置和不同壳间水位条件下的耦和作用规律,发现了破口参数小于0.5时,内舱室会出现二次涌流现象。Huang等[4]采用了5点最小二乘方法来保证破口处自由液面的光滑和稳定的运动,讨论了气泡到破口的距离、破口的大小、破口的初始深度以及重力的变化对气泡运动特性的影响。张之凡等[5]基于耦合欧拉-拉格朗日(coupled Eulerian-Lagrangian, CEL)法讨论了不完整直角结构近自由面附近气泡的动态特性,发现了在结构与自由面的共同作用下气泡出现射流偏折、水冢一侧凹陷和气泡破碎等现象。盛振新等[6]通过小当量水下爆炸试验对轰爆产物冲击带破口双层板结构进行研究,总结了炸药量、破口半径和舱室宽度对气泡运动和内板壁压的影响规律。
在数值模拟方面,边界元法、有限体积法、有限元法、CEL法、光滑粒子流体动力学法(smoothed particle hydrodynamics, SPH)等方法百家争鸣。王莹等[7]基于任意拉格朗日-欧拉法建立了爆破破冰数值模型,与试验结果吻合较好。刘云龙等[8]基于欧拉有限元方法和声学有限元场分离方法,自主编程实现了近、中、远场下的水下爆炸对结构的响应。王平平等[9]基于SPH法实现了水下爆炸气泡冲击波、脉动、与结构相互作用的数值仿真。姜忠涛等[10]基于CEL法讨论了近场水下爆炸射流在和对船体外板的冲击过程,总结了射流的载荷压力特性、速度分布及结构剪应力分布特性。目前,计算机技术在水下爆炸气泡上的应用已趋于成熟,但由于破舱结构附近交界面复杂,呈现大变形、多介质等情况,计算精度和计算时间很难保证。在试验方面,开展实船试验可以获得很好的研究效果,但是实船试验的成本过于昂贵。目前主要通过电火花试验,结合高速摄影技术进行研究,但电火花试验由于气泡尺度较小,其相似性还无法满足。目前对于破损舱室遭受二次爆炸的研究有限,且主要局限于简单的边界条件,如平板、双层板、圆柱体。破损壁面附近的气泡为气-液-固三相耦合,气泡射流冲击下结构的变形和损伤十分复杂。
针对以上问题,本文将破舱壁面简化为具有圆形破口的弹性壁面,基于CEL法建立了水下爆炸数值模型,并结合模型试验验证了数值方法。研究了气泡射流、气泡体积、脉动周期,以及气泡对壁面冲击损伤的影响,探明了不同破口参数下的气泡的脉动规律和射流穿透破口、撕裂等特征规律。为水下高能武器的研发和舰船的抗冲击提供技术支撑。
1 CEL法
在气泡动力学问题的研究中,与传统的拉格朗日方法和欧拉方法相比,CEL法结合了拉格朗日网格与欧拉网格的优点,数值模拟中拉格朗日单元的节点随物质点同步移动,而欧拉单元的节点在空间中固定不动;拉格朗日单元可以在欧拉网格内变形和运动,并且与含有材料的欧拉单元发生耦合,流体网格对结构网格施加压力,结构网格则限制流体材料的流动。可以有效地解决水下爆炸问题中有关大变形和材料破坏等诸多问题。
在数值模拟计算过程中,将结构划分为拉格朗日区域,流体划分为欧拉区域,在两种区域内分别采用欧拉有限元方法和拉格朗日有限元方法分别求解。欧拉有限元方法和拉格朗日有限元方法所使用的控制方程为流体力学中的质量守恒、动量守恒和能量守恒方程,如式(1)~(3)所示。两者之间本质区别在于:欧拉方法是对计算域的离散,而拉格朗日方法是对物质的离散。
(1)
(2)
(3)
式中:fj为单位质量的张力;e为单位质量的内能;σij为结构应力张量;qi为热通量;ρ为参考结构密度。
1.1 状态方程
在数值模拟中,材料的各项属性通常使用状态方程来描述,本文中所使用到的材料有炸药(PETN)、水、Q235碳素钢。其中,炸药采用JWL状态方程,水的状态方程采用线性Us-Up方程进行描述,整个模型采用体积分数法对气泡进行材料划分和定义。
1.1.1 炸药
本文采用的炸药为PETN,炸药的状态方程用JWL方程描述
(4)
式中:η=ρ/ρo,A、B、R1、R2、ω为炸药的各个常数;ρo为炸药密度;E为炸药能量密度;ρ为水密度,取1 024 kg/m3,如表1所示。

表1 PETN炸药的状态参数
1.1.2 水
本文采用的不可压缩黏性流体为水,其状态方程用线性Us-Up方程描述
(5)
式中:Co为流体中的声速;Γo为Gruneisen常数;ρo为流体的密度;S为声速和冲击波的传播速度之间的线性系数;Em为流体单位质量的内能。水状态参数如表2所示。此外,水的比热为4 130 kJ/(kg·℃);动力黏性系数η为0.001 Pa·s。

表2 水的状态参数
1.1.3 破损壁面
破损壁面为弹性钢板,各参数取值如表3所示。

表3 破损壁面参数取值
1.2 CEL法有效性验证
本文基于ABAQUS软件,建立了水下爆炸CEL数值模型,其中,欧拉域尺寸为12 m×7 m×12 m;钢板大小为厚度0.02 m,长0.8 m的正方形板。炸药放置在水下1 m,大于三倍气泡半径,因此忽略自由液面对气泡的影响,欧拉域仅包含水、炸药、钢板三种材料。正方形钢板垂直于破口方向的边被刚性固定,欧拉域的边界上设置边界条件无反射以模拟无限水域,设置无流入、速度为0,以模拟无穷远处边界条件。为了验证本文建立的数值方法正确性,与水下爆炸模型试验[11]进行了对比。
图1为破口参数Rh=0.25,距离参数γw=0.7下水下爆炸试验与数值模拟气泡运动特性对比图,上方一组视图(a)为水下爆炸试验,下方一组试图(b)为数值模拟结果。其中,气泡脉动时间标注在每帧图片的左上方,单位为ms。观察发现,数值模拟结果与水下爆炸试验在各个阶段保持较好的一致性。本文将基于与试验相同的距离参数研究破口对气泡动力学行为的影响。

(a) 模型试验

(b) 数值模拟
试验气泡最大等效半径为0.267 m,第一周期为45.7 ms,数值模拟计算的气泡最大等效半径为0.262 m,误差为4.81%,周期为43.5 ms,误差为1.87%。气泡表面顶点位移对比图,如图2所示。由图2可知,数值计算结果与模型试验吻合度较高,本文建立的数值方法具有较好的精度。

图2 气泡表面顶点位移对比图
2 破口参数对气泡脉动、射流以及壁面损伤研究
2.1 数值模型
实际海战中,影响气泡运动的因素诸多,为了使研究具有普遍性,本文将破口简化为圆形破口,研究破口参数Rh对其运动及损伤影响。
图3为水下爆炸数值模拟中各参数定义,Rh为破口半径;Dw为气泡中心点到破口中心点距离,Df为气泡中心点与自由液面距离,无量纲过程如式(6)所示
γw=D/Rmax
(6)
式中:D为有量纲距离;Rmax为气泡最大体积时刻的等效半径。
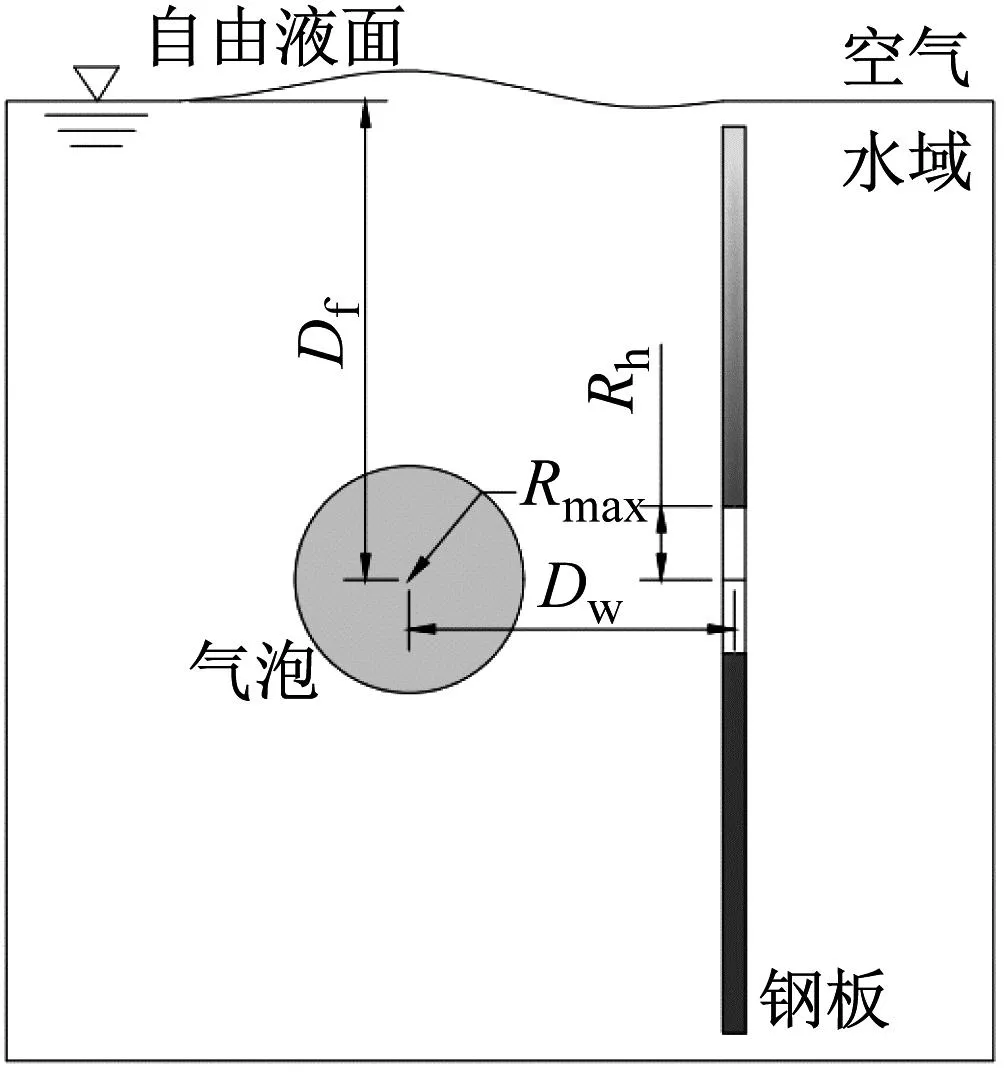
图3 试验示意图
2.2 气泡动态特性
水下爆炸气泡在不同破口参数下会呈现不同的脉动特性,为了研究破口参数对于气泡的射流、运动特性、气泡体积、周期等因素的影响,本文设置了14组工况,破口半径(无量纲)依次为0、0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.40、0.50、0.60、0.70、0.90、1.10。
2.2.1 小型破口下(Rh≤0.10)气泡脉动特性
图4为三种小破口参数下的气泡脉动特性,分别为完整壁面工况(a)Rh=0、工况(b)Rh=0.05、工况(c)Rh=0.10。为方便分析,将气泡运动特征形态采用数字帧的形式标记在图片上方(如1~7),时间标注在每张图片的左上方,单位为ms。为方便观察射流,对部气泡形态进行透视处理。

(a) Rh=0

(b) Rh=0.05

(c) Rh=0.10
第1~3帧为气泡的膨胀阶段,在小型破口参数下各工况脉动形态相似,观察体积最大时刻(第3帧),发现了从右向左的射流。这一现象的出现,是由于破口周围的气泡,在缺少壁面阻拦的情况下受到水流的冲击,此时气泡内的压力最小,远低于破口右侧流场域压力,故射流方向由右向左。破口参数Rh=0.05这一工况尤为特殊,主要表现在该射流细小,依靠气泡左侧朝向壁面收缩方能穿透气泡左表面。该现象出现的原因是破口较小,受到的冲击力有限。第4~6帧为气泡的收缩阶段,第5帧均出现了从左向右的射流,该射流是由于壁面的阻挡在气泡左侧形成高压区,同时受重力的影响,形成斜射流。为了方便分析,定义由右向左的射流为射流1(第4帧),由左向右的为射流2(第5帧)。在射流2和射流1的共同作用下,会在气泡左侧“撕裂”出部分气泡,如图4(c)破口参数Rh=0.10第6帧所示。
2.2.2 中型破口下(Rh=0.15~0.50)气泡脉动特性
图5为中型破口下(Rh=0.15~0.50)气泡脉动特性,破口参数Rh依次为0.15、0.20、0.25、0.30、0.35、0.40、0.50,上述破口参数下破口的存在对壁面Bjerknes力产生了削弱作用,但壁面对气泡仍存在一定的吸引力。第1~4帧为气泡的膨胀阶段,第2帧气泡近壁面端向破口内产生“凸进”现象。“凸进”是指在破损壁面的影响下,当气泡内气体压力发生变化时,气泡脉动过程向壁面方向挤压,相对于完整壁面,其破口位置处对气泡脉动过程限制较小,使得近破口位置处气泡向破口方向运动,甚至穿过破口结构,呈现独特的尖嘴状。研究发现,当破口尺寸较小时,破口近似于完整壁面,对气泡运动的影响很小,尖嘴状形态不明显;反之当破口参数越大,气泡右表面产生的“凸进”越明显,即涌入破口的气泡体积越大。气泡“凸进”在穿过破口后,“凸进”内压力得到释放,依靠惯性继续向右运动,破损壁面阻碍气泡主体运动,在第3帧出现了“撕裂”的现象。在较小破口参数工况中,气泡“凸进”还未穿透破口,在较大破口参数工况中,“凸进”较为圆润,较难产生“撕裂”,因此“撕裂”现象仅存在于破口参数Rh=0.20~0.40的工况中。破口参数越大,“撕裂”发生的时间越晚。气泡右表面在撕裂完成后开始收缩,收缩主要集中于破口附近的气泡局部区域,第4帧形成了从右向左的射流1。第5~6帧为气泡的收缩阶段,第5帧观察到从左向右的射流2,对比不同破口参数下的两种射流发现,射流1的半径略小于破口半径。第一周期末,射流2会再次贯穿射流1导致的环形气泡,将气泡再次“撕裂”。第7帧为气泡第二周期的脉动情况,在破口参数较大工况中,气泡体积相对较小,这是因为较大破口工况“撕裂”部分气泡会依靠惯性穿过破口脱离主体向右运动,使得气泡二次膨胀体积减小。
2.2.3 大型破口下(Rh=0.70~1.10)的气泡脉动特性
图6为大型破口下(Rh=0.70~1.10)气泡脉动特性,破口参数Rh依次为0.70、0.90、1.10,大型破口工况由于破口参数较大,壁面对于气泡产生的Bjerknes力相对较弱。第1~5帧为气泡的第一周期,在破口参数超过0.7后,气泡周围充满流体,破口难以限制壁面右侧的流体形成集中载荷冲击气泡产生射流1。破口参数Rh=0.90的工况(b)34.8 ms产生了向左的射流,该射流无法冲击气泡左表面,在气泡坍塌最小时形成环形气泡。在Rh=1.1的工况(c)中,第一周期没有观察到射流1的存在,第一周期末期形成了与自由场工况类似的斜向右上方的射流2。

(a) Rh=0.15

(b) Rh=0.20

(c) Rh=0.25

(d) Rh=0.30

(e) Rh=0.35

(f) Rh=0.40

(g) Rh=0.50

(a) Rh=0.70

(b) Rh=0.90

(c) Rh=1.10
2.3 水流冲击气泡产生的射流现象
在目前的水下爆炸气泡试验中,由于气泡内部的结构较难观察到,仅对于射流2进行了描述[11],然而研究发现射流1仍然会对气泡的形态和破损壁面产生影响。本节总结了射流1在不同破口参数下的形态特征,如图7所示,其中,破口参数标注在每个工况的左上方,时间标注在每个工况的左下方,单位为ms。

图7 不同工况射流现象
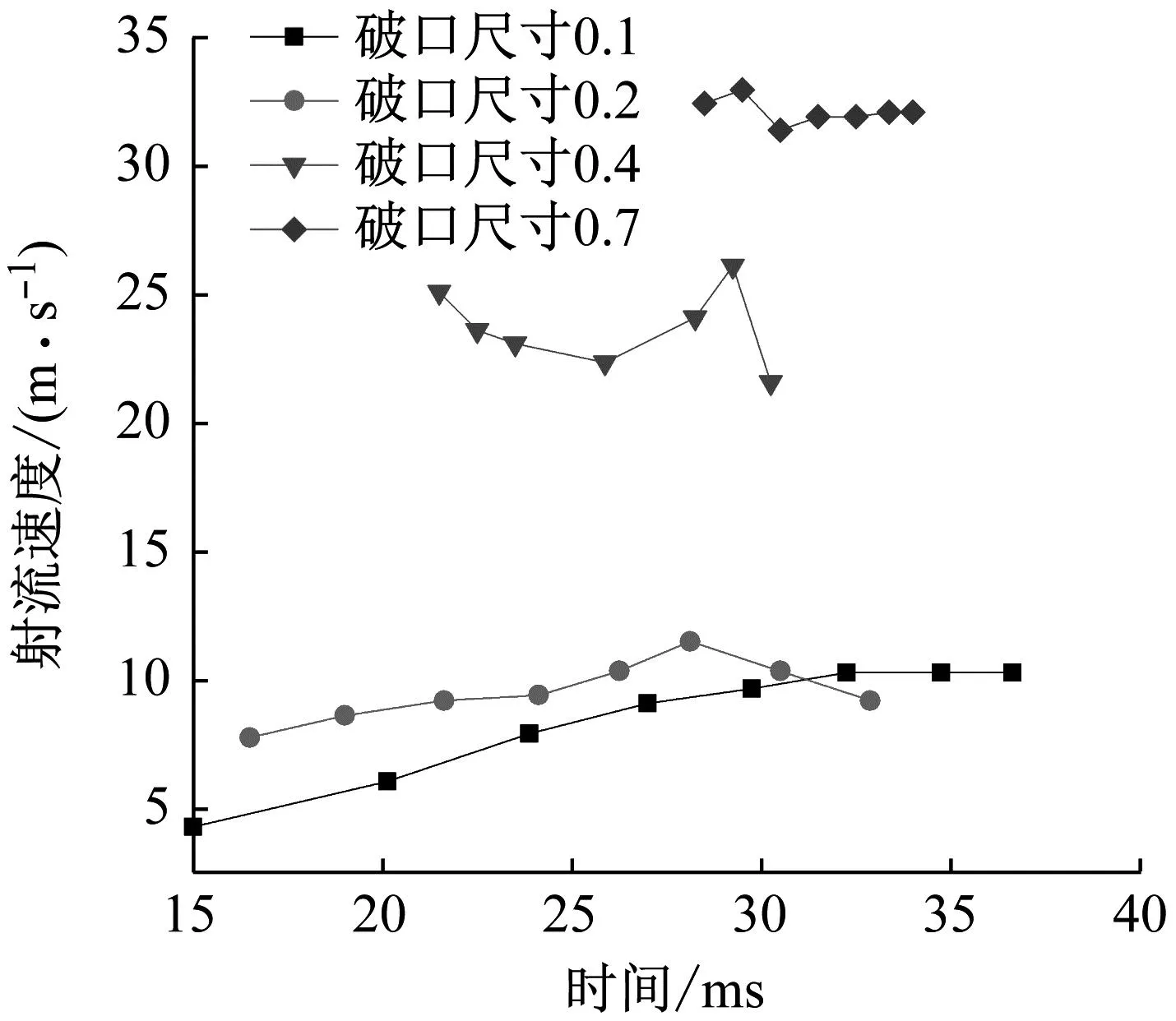
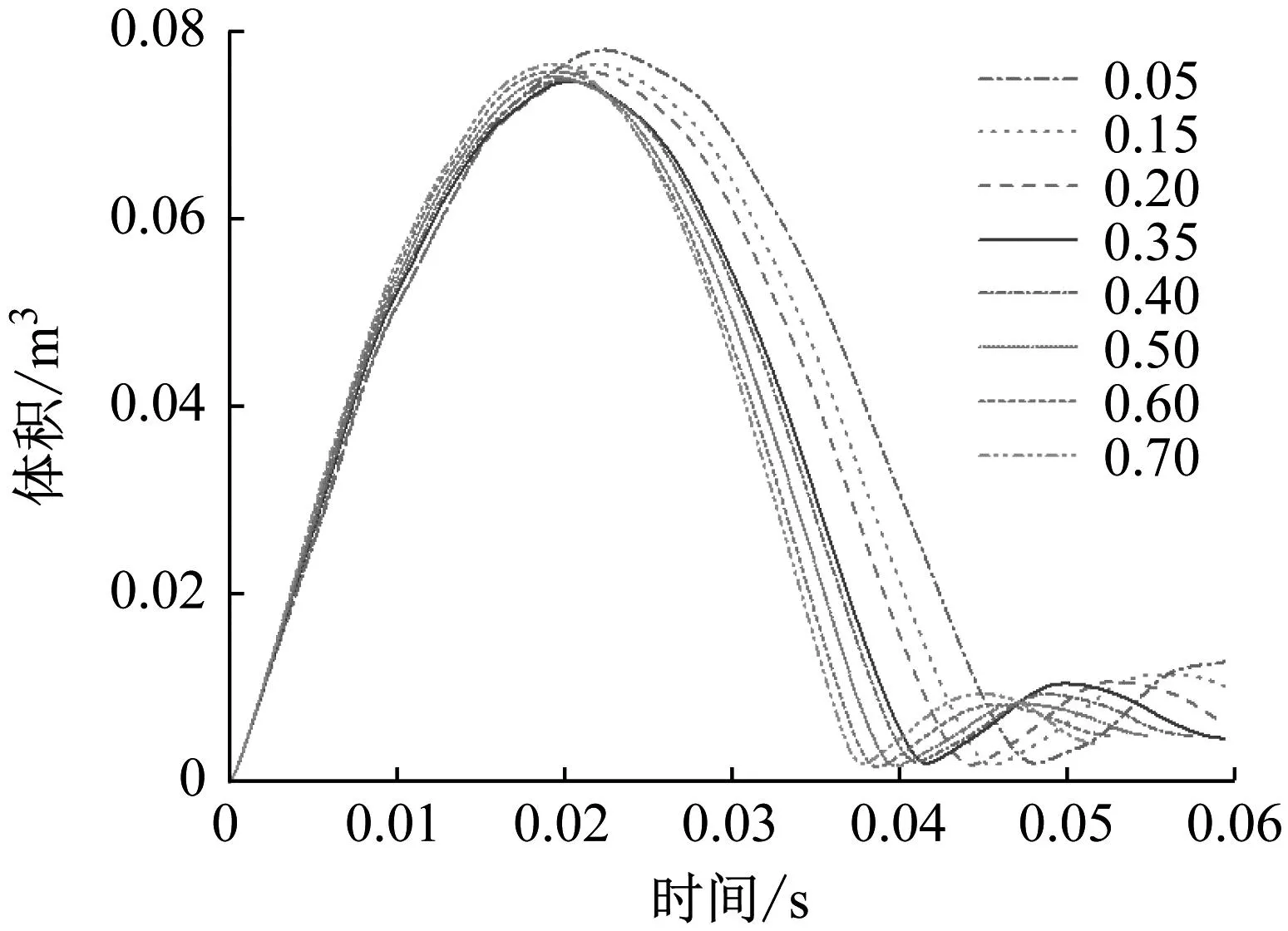
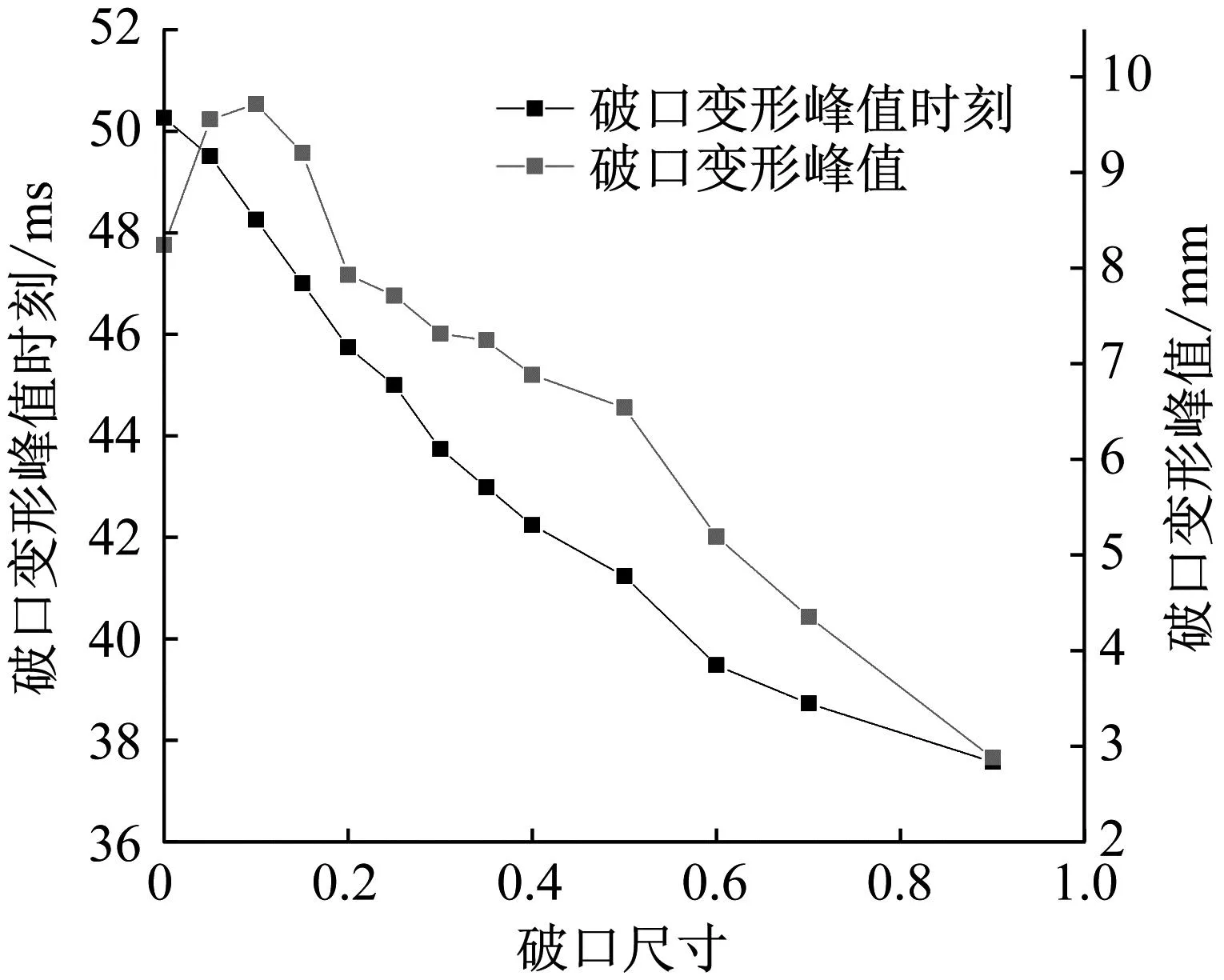
当破口参数0 图8和图9描述了不同破口参数下的射流速度,图8描述了破口影响下右侧水流冲击气泡形成的从右向左的射流1和在第一周期末期气泡左侧高压而形成的从左向右的射流2在不同破口参数下的射流速度,其中针剂型射流顶端“撕裂”导致针头状射流并不能代表射流的真实速度,选取针头末端为监测点进行测量。射流1速度一般在6~12 m/s,破口参数越大,气泡受影响的区域越大,射流1速度越快。射流2的速度一般在40~62 m/s,因此,气泡左侧高压所导致的射流2仍然是壁面造成损伤的主要原因。此外,射流1的速度和作用区间对于射流2存在削弱作用,在破口参数Rh>0.5的工况中,射流2的方向转化为由下向上甚至消失。图9描述了不同破口参数下,射流1顶端速度的时间历程曲线。射流1顶端“撕裂”形成的针头状射流速度显著高于破损壁面右侧流体冲击气泡形成的射流主体,使射流1变得复杂,最大速度一般出现在即将贯穿气泡时刻。 图8 不同破口参数下的射流速度对比图 图9 不同破口参数下的射流1顶端速度时历曲线 为了研究破口参数对于气泡动态特性的影响、分别给出气泡体积、第一周期、第二周期体积峰值、气泡周期随时间变化曲线,具体如图10、图11和图12所示。 从图10和图11中可以看出,气泡体积峰值在破口参数的影响下,整体呈现在大型破口和小型破口工况体积峰值大,中型破口工况体积峰值小的特点。这一特点在第一周期尤其明显,最小体积出现在破口参数Rh=0.35的工况中,究其原因是右侧流体冲击气泡形成的射流使右表面提前收缩,削弱了气泡后期膨胀到最大体积,减少了气泡体积峰值。 图10 不同破口参数下气泡体积时历曲线 图12 不同破口参数下气泡体积极值发生时间 国内外学者对比了多组试验,发现了壁面作用下的气泡脉动周期更长[12]。从图12中观察到:破口参数越大,气泡周期越短,且周期变短的趋势减弱。这说明破口会削弱壁面的影响,从而增大破口参数会缩短气泡脉动周期。 图13描述了不同破口参数下的破口边缘处变形峰值和发生的时间。从图13可以发现:破口参数较小时,含有破口壁面变形较大,加剧壁面损伤;破口参数较大时,壁面变形值较小,壁面的最大变形出现在破口参数Rh=0.1的工况中。此外,破口参数增加,会滞后破损壁面最大位移到来的时间。 图13 不同破口参数下破口边缘变形峰值和时间 本文基于CEL法建立了破损壁面附近水下爆炸模型,将数值结果与水下爆炸试验进行对比,验证了数值方法的有效性。对不同破口参数下的破损壁面附近气泡进行数值计算,结论总结如下: (1) 受含有破口壁面的影响,破口附近气泡运动朝向破口甚至穿过破口呈现尖嘴状的 “凸进”现象;当破口尺寸较小时,对气泡运动的影响很小,尖嘴状形态不明显;反之当破口尺寸较大时,含有破口壁面对气泡膨胀限制较弱, “凸进”现象通常出现在破口Rh=0.10~0.90的工况中。 (2) 气泡受到破口右侧水流冲击而产生的从右向左的射流,射流出现在Rh=0.05~1.10的工况中,射流宽度随破口参数增大而增大,略小于破口半径,按照其形状可总结成四种射流现象,分别为直线型、灯塔型、针剂型、沙堆型。 (3) 破口参数对气泡脉动和射流影响较大,气泡体积峰值随着破口参数的增加先增大后减小;破口参数较小时,含有破口壁面变形较大,加剧壁面损伤;气泡射流2的速度大于射流1的速度。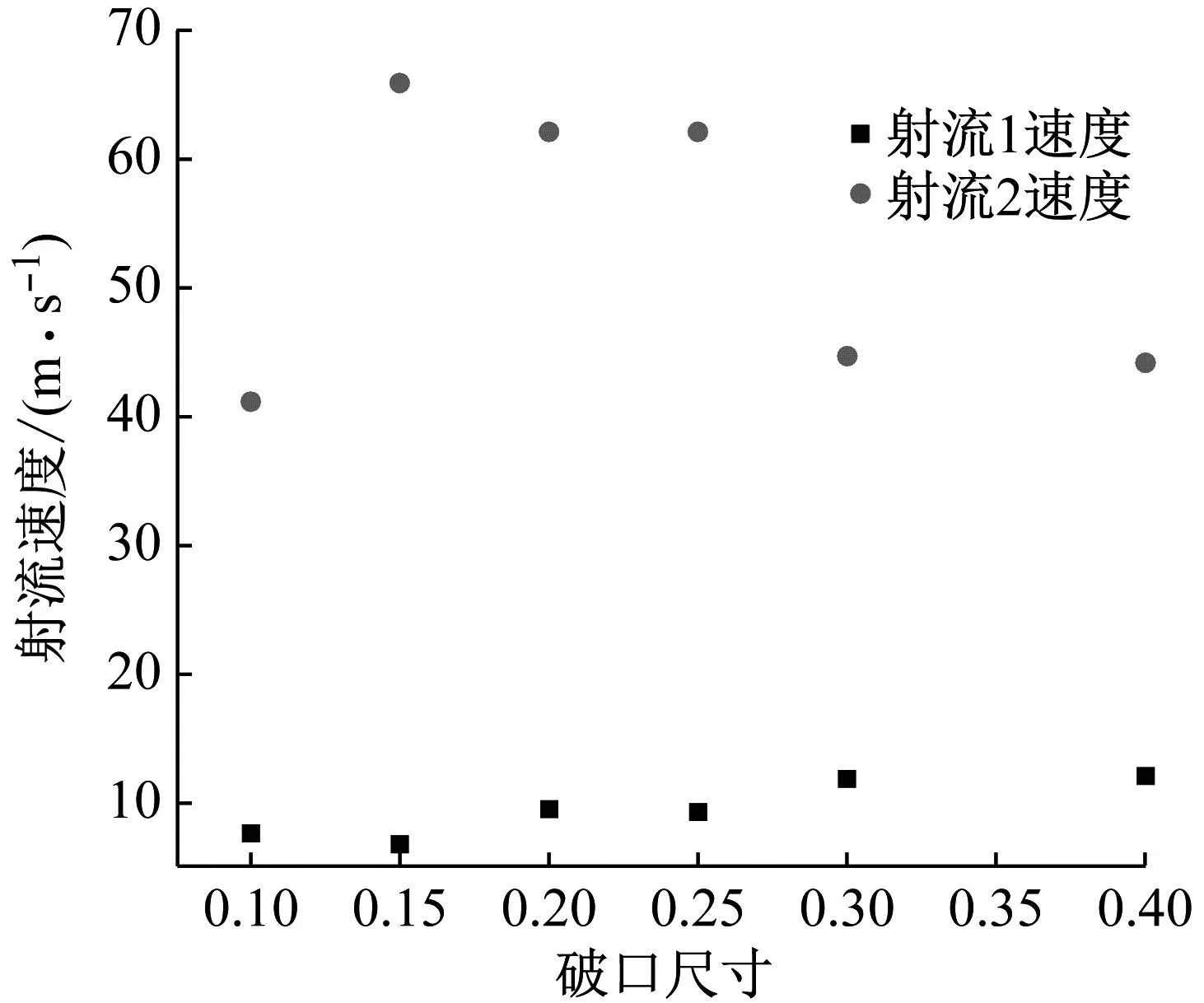
2.4 破口参数Rh对气泡和壁面损伤的影响

3 结 论

