亦说立体几何中涉及线面所成角问题

周文国

(江苏省张家港中等专业学校)

立体几何中涉及线、面所成角问题,主要有异面直线所成角问题、线面所成角问题、二面角的平面角问题等,若能掌握通性通法,则能灵活求解这类问题.

1 异面直线所成角

异面直线所成角问题是立体几何中的常见题型,其求解的方法是通过建立异面直线所成的平面角,然后视具体的问题采用不同的方法.

1.1 用平移法求解

例1 如图1所示,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,求异面直线EF与A1D所成角的大小.

图1

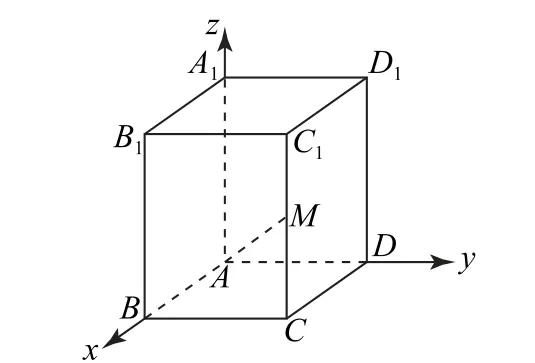
图2

分析 结合正方体的特点,可知EF//A1B,结合异面直线所成角的定义将问题转化为共面直线A1B和A1D所成角.

解 在正方体ABCDA1B1C1D1中,E,F分别是C1D1,CC1的中点,所以EF//D1C,又D1C//A1B,因此EF与A1D所成角即为直线A1B和A1D所成角.

在正方体ABCD-A1B1C1D1中,A1B＝A1D＝BD＝2AB,△A1BD为正三角形,则∠BA1D＝60°,因此异面直线EF与A1D所成角的大小为60°.

上述问题采用了求异面直线问题常用的平移法,通过平移或寻找平行直线,依托构造三角形,将异面直线所成角放在三角形中解决.

1.2 用空间向量法求解

例2 在正四棱柱ABCD-A1B1C1D1中,AA1＝2AB＝2BC＝2,点M是棱CC1的中点,求异面直线AM与BC所成角的余弦值.

分析 以A为坐标原点,建立空间直角坐标系,利用向量法确定异面直线AM与BC所成角的余弦值.

通过构建空间直角坐标系,求出异面直线的向量坐标,通常设直线l,m对应的方向向量分别是a和b,则两条直线所成角θ的余弦值cosθ＝,从而确定异面直线所成角.

1.3 用向量法求解

例3 如图3 所示,已知平行六面体ABCDA1B1C1D1的底面是菱形,且∠C1CB＝ ∠C1CD＝∠BCD＝60°,CD＝CC1＝2,求异面直线CA1与DC1所成角.

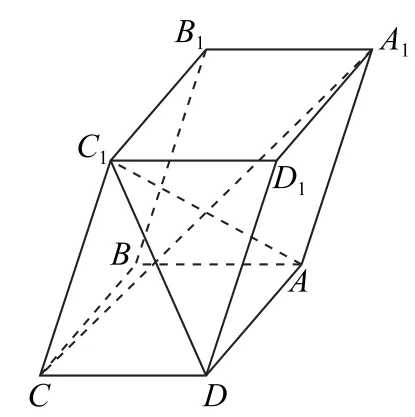
图3

分析 可以求出两条直线CA1与DC1的方向向量,再利用向量夹角的余弦公式求解.

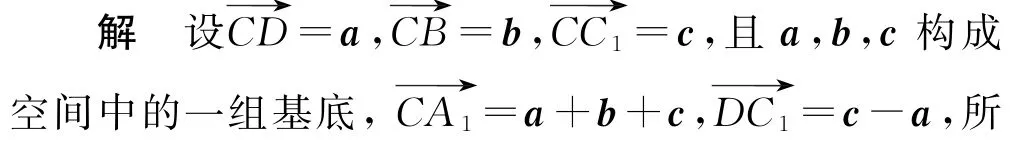
本题结合向量运算,确定两异面直线所在向量之间的位置关系,从而求出异面直线所成角的大小.

2 线面所成角问题

要求出直线和平面所成角,其关键是找到该直线在对应平面上的射影,即该直线和它的射影所成角是线面所成角.

2.1 用定义法确定

例4 (2023年全国甲卷理18)如图4所示,在三棱柱ABC-A1B1C1中,已知AA1＝2,A1C⊥底面ABC,∠ACB＝90°,点A1到平面BCC1B1的距离为1.

图4

(1)求证:AC＝A1C;

(2)若直线AA1和BB1的距离为2,求AB1与平面BCC1B1所成角的正弦值.

分析 本题的第(2)问是线面所成角问题,可结合定义找出直线AB1在平面BCC1B1上的射影,且在直角三角形中确定所成角的正弦值.

解 (1)如图5 所示,取CC1的中点O,连接A1O,因为A1C⊥底面ABC,且AC⊂底面ABC,所以A1C⊥AC,则A1C⊥A1C1,故又A1C⊥底面ABC,且BC⊂底面ABC,所以A1C⊥BC,因为∠ACB＝90°,所以AC⊥BC.因为A1C∩AC＝C,所以BC⊥平面A1C1CA,因为BC⊂平面BCC1B1,所以平面BCC1B1⊥平面A1C1CA,因为点A1到平面BCC1B1的距离为1,所以点A1到CC1的距离为1,则A1O⊥CC1,因此AC＝A1C.

图5

(2)过A作AM//A1O交C1C的延长线于M,连接MB1,取BB1的中点N,连接ON,所以四边形BCON为平行四边形,则ON⊥平面A1C1CA,且A1O∩ON＝O,故CC1⊥平面A1ON.

因为A1N⊂平面A1ON,所以CC1⊥A1N,则AA1⊥A1N,所以A1N为直线AA1与BB1的距离,则A1N＝2,所以ON＝3.

找到直线在对应平面上的射影,则该直线和射影所成的锐角或直角即为线面所成角,这是常用的确定线面所成角的方法.

2.2 用空间向量法求解

例5 (2022年全国甲卷理18)如图6所示,在四棱锥P-ABCD中,PD⊥底面ABCD,CD//AB,AD＝DC＝CB＝1,AB＝2,DP＝3.

图6

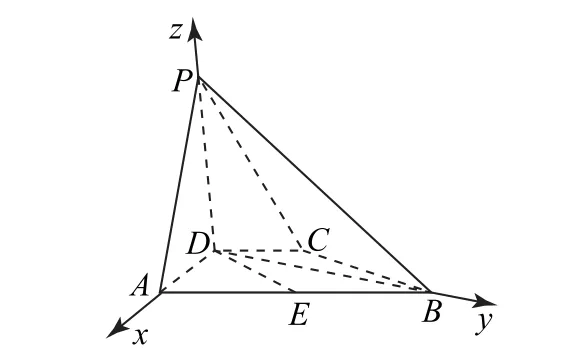
图7

(1)证明:BD⊥PA;

(2)求PD与平面PAB所成角的正弦值.

分析 可知PD⊥BD,取AB的中点E,证明四边形BCDE为平行四边形,再根据长度关系可得到BD⊥AD.通过建立空间直角坐标系,求出各点的坐标,再求出平面PAB的法向量,结合向量的夹角公式使问题获解.

解 (1)因 为PD⊥平 面ABCD,BD⊂平 面ABCD,所以PD⊥BD,取AB的中点E,连接DE,因 为AD＝DC＝CB＝1,AB＝2.又AD＝1,所以,则△ABD为直角三角形,且AB为斜边,故BD⊥AD.

又PD∩AD＝D,PD⊂平面PAD,AD⊂平面PAD,所以BD⊥平面PAD.因为PA⊂平面PAD,所以BD⊥PA.

设平面PAB的法向量为n＝(x,y,z),则

3 二面角的平面角

确定二面角的平面角方法比较多,但一般是根据所求两个平面是否有公共棱进行分类,如果是有棱,则常常通过找点或者是连线和平移的方法来确定二面角;若是无棱,则需要构造图形才能确定二面角的平面角.

3.1 用法向量求解

例6 (2023年新高考Ⅱ卷20)如图8所示,在三 棱 锥A-BCD中,DA＝DB＝DC,BD⊥CD,∠ADB＝∠ADC＝60°,E为BC的中点.

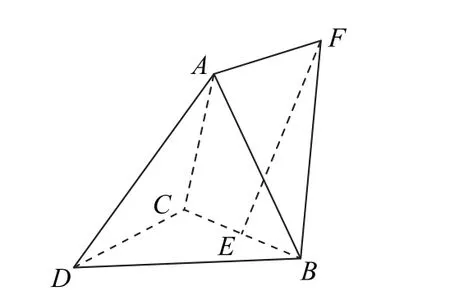
图8

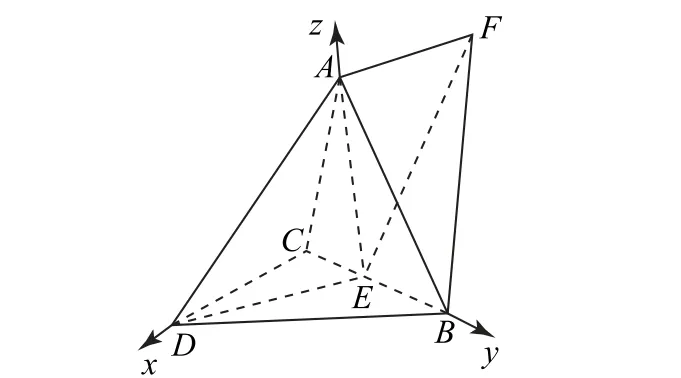
图9

(1)证明:BC⊥DA;

(2)点F满足,求二面角D-AB-F的正弦值.

分析 对于第(1)问,可得DE⊥BC,AE⊥BC,并结合线面垂直的判定定理证明;对于第(2)问,可得AE⊥平面BCD,再依次求出两个平面的法向量,利用向量的夹角公式求解.

解 (1)连接AE,DE,因为DB＝DC,E为BC的中点,所以DE⊥BC,又DA＝DB＝DC,∠ADB＝∠ADC＝60°,所以△ACD与△ABD均为等边三角形,则AC＝AB,故AE⊥BC,AE∩DE＝E,则BC⊥平面ADE,因为AD⊂平面ADE,所以BC⊥DA.

利用向量法求二面角的平面角,关键是要确定对应两个平面的法向量,再通过代数法求解.

3.2 用三垂线定理求解

例7 (2023年上海卷17)如图10所示,已知直四 棱 柱ABCD-A1B1C1D1,AB⊥AD,AB//CD,AB＝2,AD＝3,CD＝4.

图10

(1)证明:直线A1B//平面DCC1D1;

(2)若四棱柱的体积为36,求二面角A1-BD-A的大小.

分析 对于第(1)问可先证明平面A1ABB1//平面DCC1D1,再根据面面平行的性质证明;对于第(2)问,可先求出A1A＝4,再利用三垂线定理作出所求二面角的平面角,然后求解.

解 (1)结合题意可知AB//CD,AA1//DD1,且AB∩AA1＝A,所以平面A1ABB1//平面DCC1D1,又A1B⊂平面A1ABB1,所以直线A1B//平面DCC1D1.

(2)设AA1＝h,则根据题意得到该四棱柱的体积为,所以h＝4,又AA1⊥ 平 面ABCD,所以在底面ABCD内 过A作AE⊥BD(如 图11),垂足为E,因此A1E在底面ABCD内的射影为AE,再根据三垂线定理得到BD⊥A1E,∠A1EA为二面角A1-BD-A的平面角.

图11

在Rt△ABD中,AB＝2,AD＝3,所 以BD＝,则

而AA1＝h＝4,所以

故二面角A1-BD-A的大小为

用三垂线定理求出二面角的平面角,这是确定二面角平面角的常用方法,即利用三垂线定理证明两垂足的连线与棱垂直,就可找到二面角的平面角.

(完)