一道高考题的多维度视角与备考建议——以2023年北京卷第16题为例

杜 璞

(新疆维吾尔自治区石河子市东方学校)

立体几何是高中数学的重要组成部分,对于培养学生的空间想象能力和解决实际问题的能力具有重要意义.然而,立体几何的概念抽象、逻辑推理复杂、计算烦琐,很多学生在学习过程中感到困惑,解题时常常无从下手.因此,笔者结合2023 年北京卷第16题,研究立体几何的多维度视角与备考策略.

1 题目分析

题目 (2023年北京卷16)如图1所示,在三棱锥P-ABC中,PA⊥平 面ABC,PA＝AB＝BC＝1,PC＝3.

图1

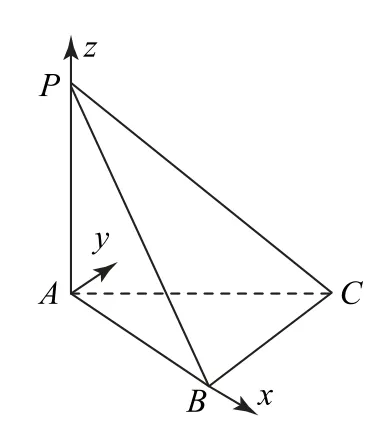
图2

(1) 求 证:BC⊥ 平面PAB;

(2)求二面角A-PC-B的大小.

分析 本题以“鳖臑”(由四个直角三角形组成的四面体称为“鳖臑”)为背景,考查立体几何的基础知识,促进了新高考与新课程、新课标与新教材的协调联动.问题设计深入浅出,设问层层递进,形式灵活.第(1)问求解过程略,本文重点探究第(2)问.

2 多维度解答视角

2.1 空间向量法

向量法是指分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐二面角还是钝二面角.第(2)问结合第(1)问中的结论,建立空间直角坐标系,分别求得平面PAC与平面PBC的法向量,再利用空间向量夹角余弦的坐标表示即可得解.

解法1 由(1)可知BC⊥平面PAB,又AB⊂平面PAB,则BC⊥AB,以A为原点,AB为x轴,过A且与BC平行的直线为y轴,AP为z轴,建立空间直

设平面PAC的法向量为m＝(x1,y1,z1),则

2.2 定义法(平面角)

在二面角的棱上任取一点(通常都是取特殊点,如中点、端点),过该点在两个半平面内分别作二面角棱的垂线,两垂线所成的角就是二面角的平面角.

解法2 如图3所示,过点B作BE⊥AC于E,连接PE,可 得BE⊥平 面PAC,BE⊥PC.在平面PAC中,过点E作EF⊥PC于F,连 接BF,由BE∩EF＝E,可得PC⊥平面BEF,则∠BFE即为二面角A-PC-B的平面角.

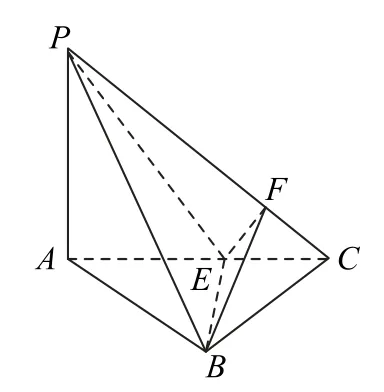
图3

图4

2.3 射影面积法(cosθ＝)

若涉及二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形的面积,则可以利用射影面积公式求出二面角的大小.本题通过确定点E(如图5)为点B在平面PAC内的投影,进而求出△PCE的面积与△BCP的面积,然后利用公式求得结果.

图5

解法4 如图5所示,过点B作BE⊥AC于E,连接PE.因为PA⊥平 面ABC,且PA⊂平 面PAC,所以平面PAC⊥平面ABC.又平面PAC∩平面ABC＝AC,BE⊂平面ABC,所以BE⊥平面PAC,则点E为点B在平面PAC内的投影,故,△PCE的面积为,△BCP的面积为

3 备考建议

针对上述多维度视角解答,本文提出以下几点备考建议.

1)加强基础知识的学习

立体几何是一门研究三维空间中形状和体积的学科,它涉及许多平面几何的相关知识和立体图形的基本性质.为了更好地理解和解决立体几何问题,我们需要深入掌握这些基础知识.

2)注重练习和总结

通过练习来熟悉各种类型的题目是至关重要的.这不仅可以帮助学生巩固所学知识,还可以让学生在面对不同问题时更加游刃有余.然而,仅仅依靠练习是不够的,在完成每一道题目后,学生还需要学会总结.这意味着要仔细分析自己在解题过程中遇到的问题和困难,找出其中的规律和不足.通过总结学生可以不断优化自己的解题思路,提高解题的效率和质量.

3)培养空间想象能力

在求解立体几何问题的过程中,空间想象能力的重要性不言而喻.这种能力不仅能够帮助学生更好地理解和分析立体几何问题,还能够提高学生在实际生活中解决空间相关问题的能力.为了锻炼和提高空间想象能力,学生可以采用多种方法和途径.首先,画图是一种非常有效的方法,通过绘制立体几何图形的草图,学生可以更直观地了解各个部分之间的关系和位置,从而更好地理解立体几何问题.此外,绘图还可以帮助学生发现问题中的规律和特点,为解决问题提供线索.除了画图之外,建模也是一种培养空间想象能力的好方法.通过构建立体模型,可以将抽象的几何概念具象化,更加清晰地看到各个部分之间的联系和作用.建模不仅可以帮助我们更好地理解立体几何问题,还可以培养我们的观察能力和动手能力.

本文通过一道高考题的多维度解答视角,揭示了立体几何在高考中的考查重点和难点,为考生提供了有针对性的备考建议.希望本文的研究能对广大师生有所帮助.

(完)