从表征到深层理解 从思维到方法建构——多视角破解几何体体积问题

林永强 巨小鹏

(1.甘肃省天水市第一中学 2.四川师范大学实验外国语学校)

本文对2021年全国乙卷文科第18题进行了多角度分析,并以此为契机对近几年常考的几何体体积问题进行了例析,从公式法、等体积法、分割法、补形法和向量法等几个方面进行归纳总结,旨在提升学生数学学科素养.

1 试题引入

题目 (2021年全国乙卷文18)如图1所示,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.

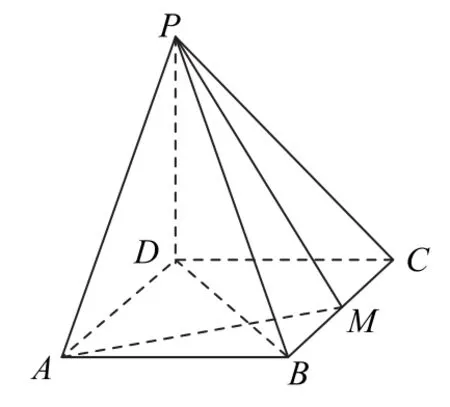
图1

(1)证明:平面PAM⊥平面PBD;

(2)若PD＝DC＝1,求四棱锥P-ABCD的体积.

2 解法探析

第(1)问要求证明平面PAM⊥平面PBD,比较简单,本文着重分析第(2)问.

方法2 (平面直角坐标系视角)由(1)可知AM⊥DB,所以kAM•kBD＝－1.建 立 如 图2 所 示的平面直角坐标系,设BC＝2a(a＞0).因为DC＝1,所以A(0,0),B(1,0),D(0,2a),M(1,a),从而

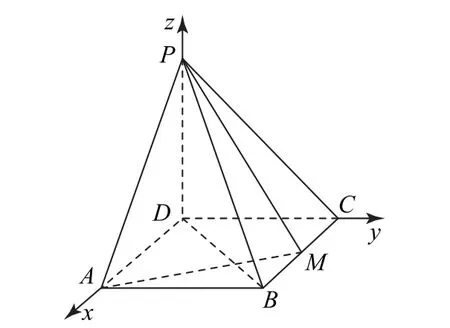
图3

BC＝2.下同方法1.

求解本题的关键是求出矩形ABCD的边长BC,方法1利用相似三角形求出矩形ABCD的边长BC,从而求得该四棱锥的体积;方法2建立平面直角坐标系,利用直线垂直的条件得到矩形ABCD的边长BC,从而求得该四棱锥的体积;方法3直接利用空间直角坐标系和空间向量垂直的坐标运算求得矩形ABCD的边长BC;方法4利用空间向量转化求得矩形的边长BC,所有解法中方法3最为简捷,可见空间向量法在解决立体几何问题中的优越性;方法5直接利用四点向量定理结论得出BC的长度,此定理在解决线线角、线面角和二面角问题都有其优越性,但需要有足够的知识储备.

3 求体积问题方法归纳与剖析

例1 在三棱锥P-ABC中,PA＝a,AB＝AC＝2a,,求三棱锥P-ABC的体积.

方法1 (体积公式视角)如图4所示,由题意可知P在平面ABC上的投影在∠BAC的角平分线AD上,记其为O,即OP为三棱锥P-ABC的高,在平面ABC内,过O作OE⊥AB于E,则AB⊥PE,即所以

图4

图5

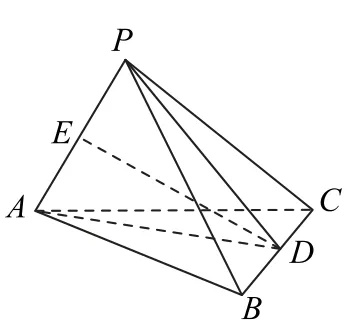
图6

本题考查三棱锥的几何特征和体积,考查了问题分析求解能力.以往高考直接考查公式的试题居多,比如2021年全国甲卷第11题,全国Ⅱ卷第5题,2020年海南卷第13题,2018年全国Ⅰ卷第18题,天津卷文科第11题,2017年全国Ⅰ卷文科第18题,新高考Ⅱ卷文科第18题等.

方法2 (等体积视角)在△PAB中,根据余弦定理可 得PB＝ 3a,则,同理,可得,所以AP⊥平面PBC,则

若直接求体积不好求,则可以转变角度利用等体积法求解.等体积法常用于解决点到平面的距离问题,是文科卷中常考查的方法.

通过分析题中几何体的特征,方法3将三棱锥P-AMN分割成以a为棱长的正四面体,根据底面面积之比得出体积.方法4根据三棱锥几何特征,将三棱锥平分,进而利用分割思想解决问题.

方法5 (补成正四面体视角)延长AP到Q使得AQ＝2a,连接QB,QC,则三棱锥Q-ABC是以2a为棱长的正四面体,所以Q到平面ABC的距离是P到平面ABC的距离的2倍,则

方法5相当于对方法3的一种优化处理,计算更加简单.割补同属于一种思想,分割是向内视角,补全是向外视角,但是大多数时候学生首先想到的是分割处理,向外的补全视角不易想到,为了强化此种意识,应将割补分为两类进行归纳总结.

例2 (2018年江苏卷10)如图7所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为_________.

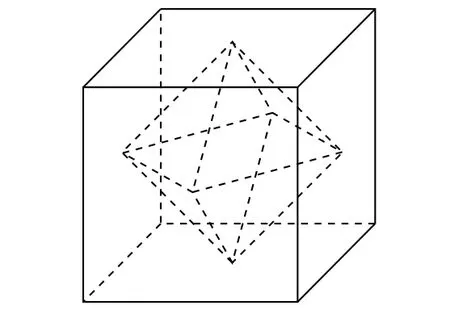
图7

由图可知该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于2,所以所求多面体的体积为

解决此类问题的关键是准确理解几何体的结构特征,可以判断所求几何体可以分割为两个全等的四棱锥,因此考虑采用割补法求解.

例3 (2019 年全国Ⅰ卷理12)已知三棱锥P-ABC的四个顶点在球O的球面上,PA＝PB＝PC,△ABC是边长为2 的正三角形,E,F分别是PA,AB的 中 点,∠CEF＝90°,则 球O的 体 积 为( ).

方法1 如图8所示,因 为PA＝PB＝PC,△ABC是 边 长为2 的正三角形,所以P-ABC为 正 三 棱 锥,则PB⊥AC.又E,F分别为PA,AB的中点,所以EF//PB,故EF⊥AC,而EF⊥CE,CE∩AC＝C,所以EF⊥平面PAC,PB⊥平面PAC,则∠APB＝90°,因此PA＝PB＝PC＝2,结合勾股定理易知PA,PB,PC两两相互垂直,故P-ABC为正方体一部分,,故,所以选D.

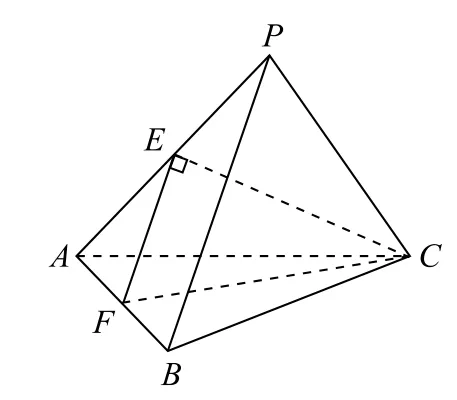
图8

方法2 如图9所示,设PA＝PB＝PC＝2x,因为E,F分别为PA,AB的中点,所以EF//PB,且

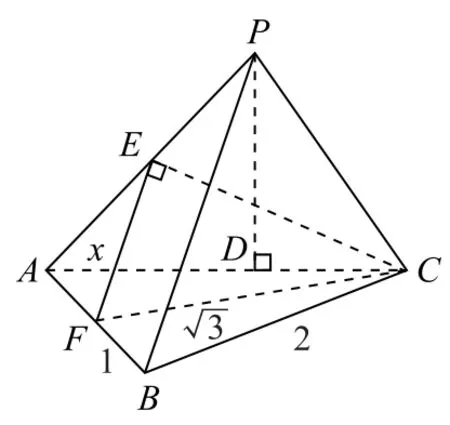
图9

本题考查学生的空间想象力,可通过线面垂直定理得到三棱两两相互垂直的关系,进而利用补全法解决问题.求体积问题并非只考查一种方法,有可能综合考查公式法、等体积法以及割补法,需要综合分析问题.常见的补全法有将正六边形放在正方形中,将三棱柱补成平行六面体,三棱锥补成四棱锥、三棱柱或平行六面体,将圆锥放在圆柱中,从而利用整体和全局意识解决问题.

当然解决此类问题的方法远不止于此,还有平移法、相似比法、祖暅原理法和积分法等.建构主义认为,学生学习从简单阶段出发,通过逐步渗透,创造出复杂规则或高级规则,目的是解决一个或一类实际问题,然后进入结构化阶段,将离散的图式变得连续起来,最后进入迁移阶段,达到更为抽象的思维水平,呈现出丰富性、特殊性和发展性的特点.通过认知分析,找到合适的方法,甚至对比分析在不同的方法,进而形成解决此类问题的解题思维体系.

(完)