从2023年新高考Ⅰ卷立体几何解答题谈备考建议

胡 坤

(江苏省外国语学校)

高考题对学生复习备考具有重要意义.2023年新高考Ⅰ卷第18题对立体几何的考查难度有所下降,但多数考生在本题的得分却并不高.笔者收集了一些考生的作答情况,探究其使用的方法并分析错误原因,提出了一些备考建议.

1 原题重现

题目 (2023年新高考Ⅰ卷18)如图1所示,在正四棱柱ABCD-A1B1C1D1中,AB＝2,AA1＝4.点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2＝1,BB2＝DD2＝2,CC2＝3.

图1

(1)证明:B2C2//A2D2;

(2)点P在棱BB1上,当二面角P-A2C2-D2为150°时,求B2P.

分析 自2021 年起,新高考Ⅰ卷便没有文理之别.往年立体几何解答题一般以棱柱和棱锥为载体分步设问,第(1)问常以平行、垂直的证明为主;第(2)问主要考查线线角、线面角和二面角的计算,两问合为一证一算,今年依旧是这样的形式.2023新高考Ⅰ卷立体几何题共22分,分为1道多选题、1道填空题、1道解答题,分数占比约为14.7%.

2 解析及常见错解

2.1 第(1)问的五种证法

证法1 构建平行四边形,利用平行的传递性证明.为了排除动点P的干扰,这里隐去点P.如图2 所示,作A2N//AB交BB1于 点N,D2M//CD交CC1于 点M,则A2ND2M,四边形A2NMD2是平行四边形,故

图2

又B2NC2M,四边形B2NMC2是平行四边形,故

由①②知B2C2//A2D2.

同类解法还有3种,可把辅助线MN转移至其他位置(如图3),形成了由A2B2C2D2和MN建构的三个平行四边形,以其中两个证明另外一个.

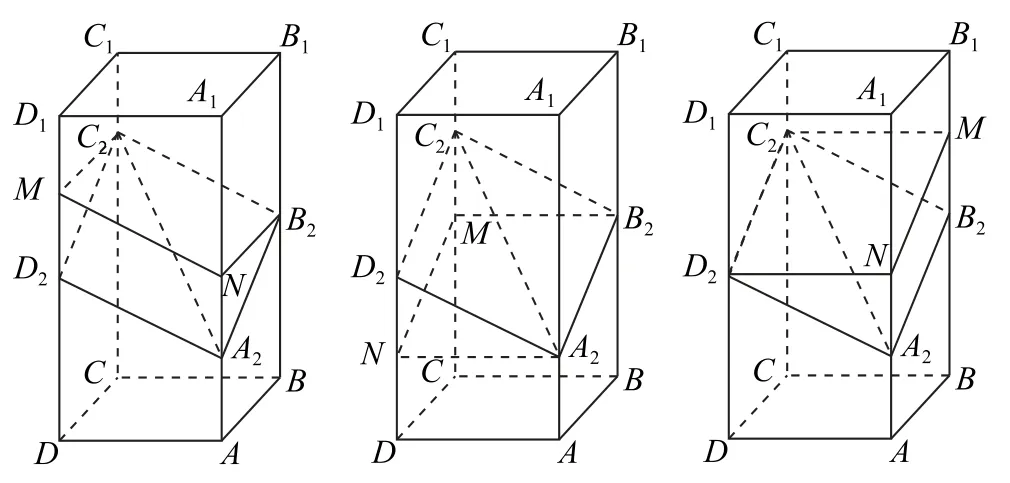
图3

证法2 同样是构建平行四边形,利用平行的传递性来证,只是添加辅助线不同.如图4所示,可分别作AN//A2D2,BM//B2C2,易得四边形ABMN是平行四边形,故AN//BM,又AN//A2D2,BM//B2C2,故B2C2//A2D2.

图4

类似地,还可以在上方添加辅助线,如图5所示,证法一致.

图5

图6

还有其他的建系方式,原理是一致的.其他建系方式只要将上述关键点的横、纵、竖坐标进行轮换即可,这里不再赘述.

证法4 四点共面,结合面面平行性质定理证明.如图7 所示,建立空间直角坐标系,则B2(0,2,2),D2(2,0,2),故B2D2的中点坐标为(1,1,2).同理,可得A2(2,2,1),C2(0,0,3),则A2C2的中点坐标为(1,1,2),故B2D2和A2C2的中点是同一个点,记为O(1,1,2).

图7

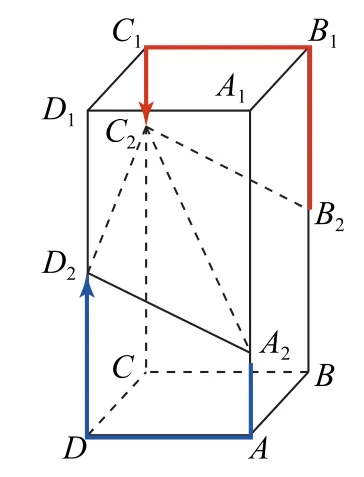
图8

该方法十分简便,充分利用平面向量的性质,需要学生对空间中的平面向量有一定的把握.另外,由于图已表明B2C2和A2D2不在同一条直线上,故可由向量相等直接得出平行.

2.2 第(1)问常见错解

采用全等来证明是最常见的错误.如图9所示,作几条辅助线构建两组全等的直角三 角 形,△B2C2M≌△A2D2N,△C2D2H≌△B2A2R,由对应边相等得四边形A2B2C2D2为平行四边形(也是边长为5的菱形),则B2C2//A2D2.该方法的错误在于忽视了要证四点共面,四点不共面,两组对边分别相等,不一定是平行四边形,可以用空间四边形(二面角)作反例.

图9

部分学生想到用面面平行性质定理证明,但同样忽视了要证四点共面.“坐标法”有用左手系的,虽不恰当,但运算正确原则上不扣分.

书写方面,向量不加箭头、向量坐标不加等号这类错误较为常见.此外,添加新的辅助线,字母尽可能避免出现很多下标,本题已有A1B1C1D1和A2B2C2D2,若再写A3B3C3D3,则容易出现书写纰漏,采用MN这样的字母可以很好地规避.

2.3 第(2)问的解法

2.4 第(2)问常见错解

建系方式不同,点P的坐标设法不一,常见的点P的坐标设法主要有P(0,2,t),P(0,2,4t),P(0,2,2＋t),P(0,2,2＋2t)等,其中4t和2＋2t是采用向量共线设点方式得到的,2＋t是设B2P＝t得到的.

题中已将点P标在B2上方,这使得部分学生将结果中的t＝1舍去,但这并不能全算学生错误,也反映了题目具有争议.

二面角为150°使得最终结果为1,调查发现,很多学生的解题过程有错误,但结果都为1,甚至有做不出来,猜结果为1的,看似答案正确,实际上不得分.本题若将150°改为135°,那么最终结果为3,不容易猜出答案,但值得注意的是,3虽更有区分度,但也会使得计算变得更复杂,不侧重知识点的考查,值得讨论.

若|cos150°|＝|cos‹m,n›|中不加绝对值符号,则结果为,随后再平方处理,这种错误实质上是对法向量所成角与二面角的大小关系为相等或互补没有把握.

还有一些常见错误,由于建系不当、引入分数坐标、法向量不化简等,导致t解不出来,这些错误既花费了大量时间,又不得分,得不偿失.

3 从高考题谈备考建议

1)注重方法,优化运算.

第(2)问要建系,不妨在第(1)问就建系做,用向量相等证平行,最直截了当.因此,要注重选择解题方法,停一停再动笔,多想一些,慢算一些,“磨刀不误砍柴工”.运算方面,争取一笔到底,不走回头路.例如,若将点P的竖坐标设为2＋2t,后面法向量求解容易出错;法向量尽可能取整数,使得代入运算变得简单.目前,学生对含有分数、根号、负号的运算有些畏惧,建议总结与练习.

2)合理分布书写空间,得分点要写在醒目的位置,图也是答案的一部分.

书写要讲究“美观”,养成良好的习惯,条件不能漏,字迹要工整,字母书写注意下标.当含有较多下标字母的时候,尽量用不含下标的字母规避.作答前,要预先规划书写区域,采用“上下＋左右”结构,得分点写在醒目位置.另外,图也是答案的一部分,由于答题卡上的图没有辅助线痕迹,导致扣分的情况已屡见不鲜,建议先在试卷上画草图,确认无误后再转移到答题卡上.

3)过程不跳步、详略得当.

中档题拿不到满分,常见的问题就是过程详略不当,“想得快、写得乱”是多数学生的通病.例如,求法向量,答题卡上写“易得平面A2C2D2的一个法向量为m＝(1,1,2)”;再比如,对于余弦绝对值的式子,不少同学省略运算细节,直接得出结果,或猜出结果(两解猜其一),省略计算过程,都属于解题不规范.平时复习备考要重视步骤分、过程分.

4)回归教材、研究真题.

新高考没有热门和冷门知识点一说,不能过度依赖模拟卷的出题套路,四点共面和性质结合突出了今年高考对基础知识的考查.建议考前复习回归教材,夯实基础,以真题为蓝本.章建跃曾表明,新教材的题目注重对知识的“识记”与“理解”,在一定程度上提高了推理题的比例,注重培养学生推理论证的能力,新高考更加注重考查学生的逻辑推理能力.

5)适当用好教育大数据平台.

科技的发展使得一些优质的模拟题和真题卷都能在一些平台上获取.借助大数据平台,可快速筛选出适合自己的题目加以训练,通过一题多解、一题多变的方式达成“横向对比找差距、纵向选题强化训练”的目标.

4 小结

立体几何是高考的重要内容,它对培养学生空间想象能力、数学抽象能力和逻辑推理能力起到了关键作用.学生从平面几何过渡到空间立体几何面临着诸多困难,高考题的研究无疑是发现问题和解决问题一种有效途径.著名教育家杜威说过“教学即生长”,立体几何学习不是格式化、模式化的被动接受,而是以发现问题、改正错误的方式启发学生自主成长.

(完)