探究立体几何最值问题的常用求解策略

桓 坤

(江苏省沛县中学)

以立体几何图形为载体,考查有关最小值或最大值问题,能够较好地考查学生的综合运用能力,进一步提高空间想象能力、逻辑推理论证能力以及运算求解能力,同时能够拓宽学生的解题思维,积累解题经验.

1 考虑侧面展开图,巧解有关最小值问题

求解立体几何表面上两点间的最短距离或立体几何表面上几条线段长度之和的最小值时,往往需要先画出该几何体的侧面展开图,这样有利于将立体几何问题转化为平面几何问题,从而从平面几何的角度去探求最小值,进而顺利解决目标问题.

例1 在长方体ABCD-A1B1C1D1中,AB＝1,AD＝AA1＝2,点E是棱AA1上的一个动点,设平面BED1与棱CC1交于点F,则四边形BED1F周长的最小值为( ).

为了便于分析,先画出长方体ABCDA1B1C1D1,如图1所示,再画出其侧面展开图,如图2所示.由图易知,当BD1∩AA1＝E,BD1∩CC1＝F时,截面四边形BED1F的周长取得最小值.

图1

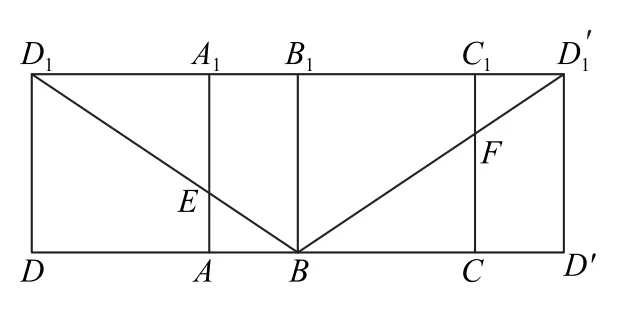
图2

求解的关键是考虑几何体的侧面展开图,将立体几何问题转化为平面几何问题,从而有利于具体分析最小值,然后借助有关平面几何知识加以求解计算.

2 利用不等式的性质,巧解有关最值问题

求解有关几何体体积的最值或有关空间角的某个三角函数值的最值时,往往需要借助图形进行适当分析,再灵活运用重要不等式a2＋b2≥2ab(其中a,b∈R,当且仅当a＝b时,等号成立)或基本不等式(其中a≥0,b≥0,当且仅当a＝b时,等号成立)巧妙求解目标最值问题.

例2 如图3 所示,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,点Q在平面PAD与平面PBC的交线上,且已知PD＝AD＝1,则直线PB与平面QCD所成角的正弦值的最大值为_________.

图3

设平面PAD与平面PBC的交线为直线l,先证明直线l⊥平面PCD.

由四边形ABCD为正方形,得AD//BC,又因为AD⊄平面PBC,BC⊂平面PBC,所以根据线面平行的判定定理可得AD//平面PBC.

于是,结合AD⊂平面PAD,且平面PAD与平面PBC的交线为直线l,根据线面平行的性质定理可得AD//l.由于四边形ABCD是正方形,则AD⊥CD,由PD⊥底 面ABCD,得PD⊥AD,又PD∩CD＝D,所以根据线面垂直的判定定理,可得AD⊥平面PCD.因此,直线l⊥平面PCD.

如图4所示,建立空间直角坐标系D-xyz,可得点P(0,0,1),B(1,1,0),C(0,1,0),D(0,0,0).因为直线l⊥平面PCD,且点Q∈l,所以可设点Q(m,0,1),其中m＞0,则

图4

题目设计比较新颖(没有具体给出两面的交线),需要先探究图形特征(两面的交线垂直平面PCD),再利用空间向量法,求解线面所成角的正弦值的代数式,最后在适当变形的基础上,活用基本不等式的变形式a＋b≥2ab顺利求解问题.

3 利用函数的单调性,巧解最值问题

求解有关简单几何体体积的最值时,往往需要在“设元”分析的基础上,先获得该几何体体积的函数表达式,再通过构造函数,借助导数分析函数的单调性,进而利用函数的单调性顺利求解目标最值问题.该求解策略充分体现了“数形结合思想”“等价转化思想”以及“函数与方程思想”在解题中的综合运用,有利于较好地培养学生的综合素养.

例3 在三棱锥P-ABC中,已知平面PBC⊥平面ABC,且∠ACB＝90°,BC＝PC＝2,若AC＝PB,则三棱锥P-ABC的体积的最大值为________.

如图5 所示,为了便于分析、求解,先画出对应的三棱锥.设PB＝AC＝x,则易知0＜x＜4.因为∠ACB＝90°,即AC⊥BC,又 平 面PBC⊥平 面ABC,AC⊂平面ABC,且平面PBC∩平面ABC＝BC,所以根据面面垂直的性质定理,可得AC⊥平面PBC.于是,有.在△PBC中,由余弦定理得

图5

所以

从而,可知

于是,根据式①②可以解得VP-ABC的最大值为

本题具有一定的综合性,需要先根据“等积法”和解三角形知识获得三棱锥P-ABC体积的函数表达式,再灵活运用构造函数的思想巧妙求解目标最大值.△PBC面积的求解,还可以运用等腰三角形“三线合一”的性质简捷获解,易知PB边上的高为,所以

总之,关注立体几何中有关最值问题的常用求解策略,可帮助我们熟知常见题型、常用解题方法,有利于较好地提升学生在直观想象、数学抽象、逻辑推理以及数学运算等方面的核心素养.

(完)