立体几何因正方体而精彩

王红妮

(山东省荣成市第二中学)

正方体是特殊的空间几何体,有丰富多彩的性质,是高考考查学生空间想象能力的重要考点,既可以作为命题点直接考查,也可以作为解题的载体,即构造正方体,将其他线、面、角或几何体置于其中,从而借助正方体直观解决问题.

1 正方体是处理线、面、角关系的载体

正方体的六个面均为正方形,又称正六面体,线面的平行、垂直或夹角等特殊关系在正方体中都有直接的体现,因此在判断线、面的位置或角的大小时,可将题目中所涉及的几何量置于正方体中,从而直观展示这些关系.

例1 已知直线a和平面α,β,α∩β＝m,a⊄α,a⊄β,a在α,β内的射影分别为直线b和c,则b,c的位置关系是( ).

A.相交或平行 B.相交或异面

C.平行或异面 D.相交、平行或异面

将题目条件中所给的线、面置于正方体中,如图1 所示.令平面ADD1A1为α,平面ABCD为β,则AD＝m.当B1C1＝a时,b//c;当A1B＝a时,b∩c＝A;当D1B＝a时,b,c异面,故选D.

图1

2 正方体的性质是高考命题的常考考点

如图2所示,在正方体ABCD-A1B1C1D1中有如下性质.

图2

1)A1C⊥平面AB1D1,A1C与平面AB1D1的交点为A1C的三等分点,平面AB1D1与正方体的12条棱所成的角均相等;

2)在侧面或底面正方形,如在正方形ABCD中(如图3),E,F分别为棱AB,BC上的点,且AE＝BF,则DE⊥AF.

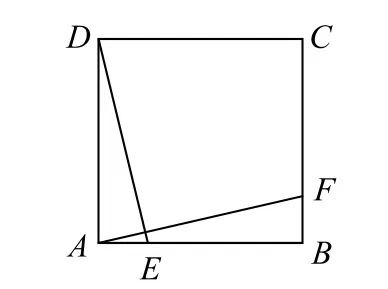
图3

这些性质的证明较为容易,此处略.当然类似的性质还有很多,不再一一列举,解题中如果能够灵活应用这些性质,则可使问题顺利获解.

例2 如图4 所示,在棱长为1 的正方体ABCDA1B1C1D1中,若 点E是 棱AB的 中 点,点M是 底 面ABCD内的动点,且满足A1M⊥C1E,则线段AM的最小值为( ).

图4

本题条件中给出A1M⊥C1E,其中M为动点,A1M为动线,C1E为定线.欲求AM的最小值,要先确定点M的轨迹.

定线C1E与动线A1M垂直,则动线A1M在与C1E垂直的平面内,进而构造该平面.如图5 所示,设BC的中点为P,连接A1D,PD,CE,C1B.

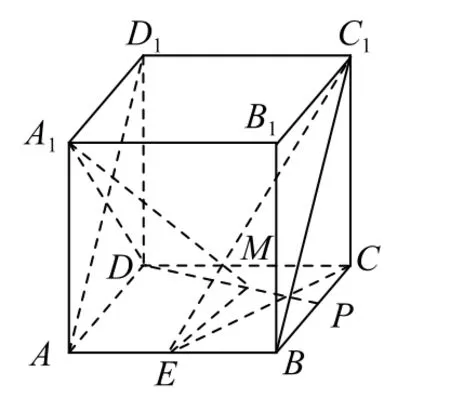
图5

由性质2)可知DP⊥CE,又CC1⊥DP,CC1∩CE＝C,所以DP⊥平面C1CE,所以DP⊥C1E.因为A1D⊥平面AD1C1B,C1E⊂平 面AD1C1B,所 以A1D⊥C1E.而A1D∩DP＝D,所以C1E⊥平面A1DP,因为A1M⊂平面A1DP,又M在底面ABCD内,所以M为线段DP上的点.当AM⊥DP时,AM取得最小值.再利用平面几何知识易求得此时,故选B.

例3 已知正方体ABCD-A1B1C1D1的棱长为2,平面α与正方体的所有棱所成的角均相等,则平面α截正方体所得截面面积的最大值为( ).

平面α与正方体的所有棱所成的角均相等,由性质1)可知平面α//平面A1BC1(如图6),据此构造平面α截正方体的截面.如图7所示,在D1C1上任取一点E,在平面A1B1C1D1内过点E作EF//A1C1交A1D1于点F;再过点F在平面ADD1A1内作FG//BC1交AA1于点G,采用同样的方法得到六边形EFGHIJ即为平面α截正方体所得截面的一种情况.

图6

图7

将正方体的侧面ADD1A1与A1B1C1D1展开置于同一平面内,如图8所示,根据正方体的对称性可知E,F,G三点共线,且EF＋FG＝A1C1,进而可得六边形EFGHIJ的周长为定值,故当EFGHIJ为正六边形时面积最大,此时正六边形的边长为2,故面积为3 3,选C.

图8

3 正方体是某些特殊几何体的母体

某些特殊几何体可以看成是由正方体切割得到的,如正四面体是由正方体去掉四个三棱锥得到的,因此在处理正四面体相关问题时,可将其还原到正方体中.

例4 已知棱长为2的正四面体P-ABC的顶点A,B分别在空间直角坐标系O-xyz中的x轴,y轴上移动,则|OP|的取值范围是( ).

将正四面体PABC置于正方体中,如 图9 所 示,因 为∠AOB＝90°,所以点O到AB中点的距离为1.由球的定义可知点O在以AB为直径的球上,则|OP|即为球面上一点O与球外一点P的距离.由已知得球心为AB的中点,其到点P的距离为3,所以|OP|max＝3＋1,|OP|min＝3－1,所以|OP|的取值范围是[3－1,3＋1],故选A.

图9

例5 连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角α(0°＜α＜360°),使该几何体与自身重合,那么称这条直线为该几何体的旋转轴.如图10 所示,八面体的每一个面都是正三角形,并且四个顶点M,N,P,Q在同一平面内,则这个八面体的旋转轴共有( ).

图10

A.7条 B.9条 C.13条 D.14条

由题目条件可知该几何体为正八面体.如图11 所示,取正方体ABCD-A1B1C1D1各面的中心构造正八面体,结合正方体的性质可知相对的两个顶点的连线,即MP,NQ,EF所在的直线为旋转轴,共3条.

图11

连接棱的中点,即ME与PF,NE与QF,PE与MF,QE与NF,MQ与NP,MN与PQ中点的连线所在直线均为旋转轴,共6条.

连接各面的中心,即平面MNE与平面PQF,平面NPE与平面MQF,平面PQE与平面MNF,平面MQE与平面NPF中心的连线所在直线均为旋转轴,共4条.

综上,该几何体的旋转轴共有13条,故选C.

高考试卷中立体几何试题中所涉及的几何体,许多与正方体有关,我们除了要熟练正方体的相关性质外,还要有意识地以正方体为依托,建立其他线、面或角的大小,从而利用正方体的直观性解题.

(完)