强基计划数学备考系列讲座(21)——立体几何中的几何计算

王慧兴(正高级教师 特级教师)

(清华大学附属中学)

立体几何中的几何计算包括距离、角、体积以及与球面关联的几何计算.在面向高考的常态教学中,常以向量坐标法为重点,为实现教学与考查的全面性,高校强基校考命题更注重考查几何体的几何性质、基于逻辑推理的几何分析能力与计算能力.支撑几何计算的基本图形是三角形,在求距离或求角时,基本路径都是通过寻求一个与求解目标相关联的三角形来完成计算.

1 求几何体中的距离

1.1 内容提要

空间距离的类型共有6种,如表1所示.求空间距离时应选择合适的位置并作出对应的线段,将问题转化为求两点间的线段长,最终在一个三角形中由勾股定理或余弦定理完成计算.

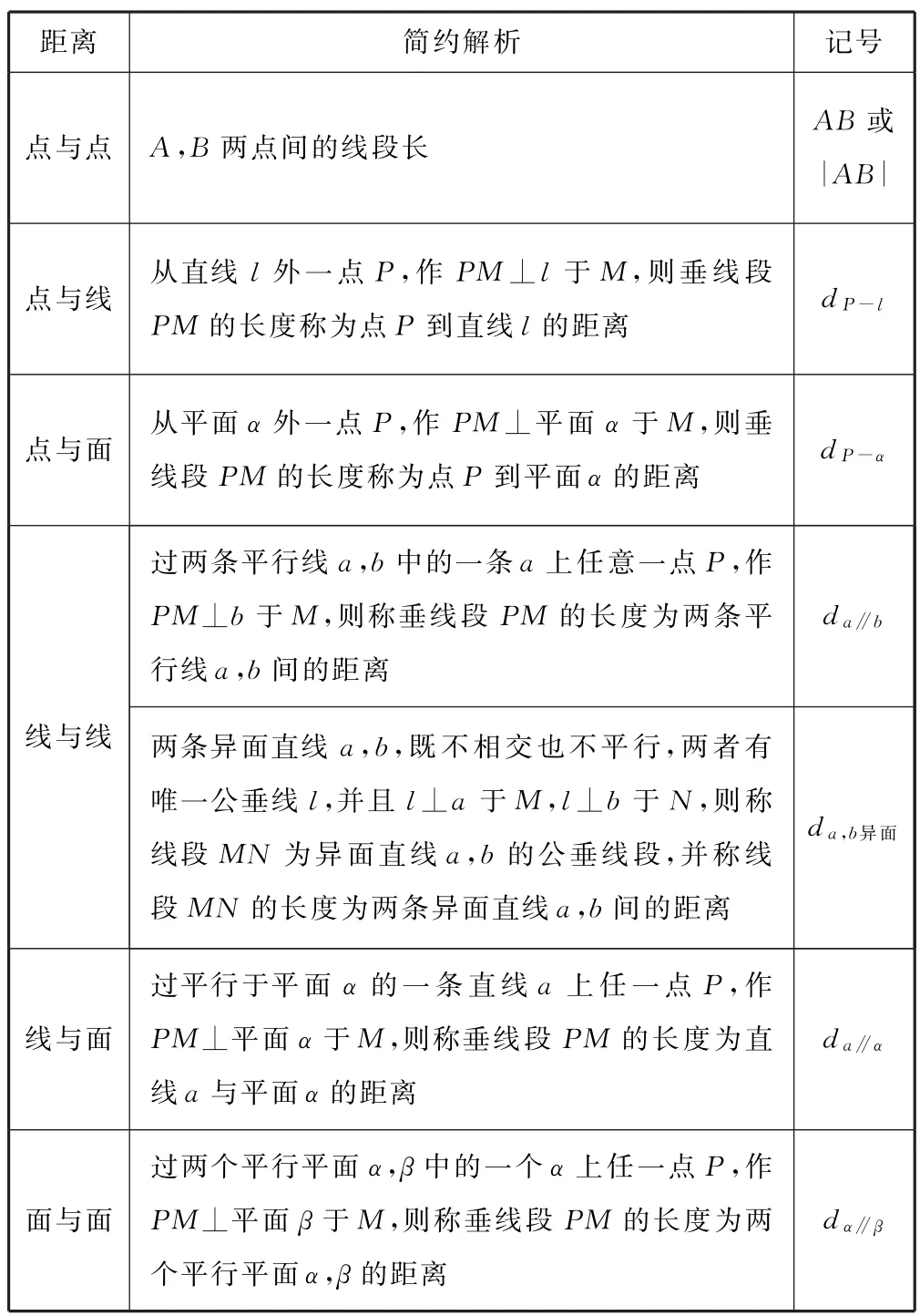
表1

1.2 典例精析

例1 (清华大学)在四棱锥P-ABCD中,已知∠APB＝∠APD＝∠PBC＝∠PDC＝90°,PA＝PB＝PD＝BC＝CD＝2,则四棱锥P-ABCD的高为( ).

如图1所示,因为∠APB＝90°,PA＝PB＝2,所以AB＝2 2.同理,PC＝2 2,AD＝2 2.由得AC垂直平分线段BD,且垂足M是线段BD的中点.

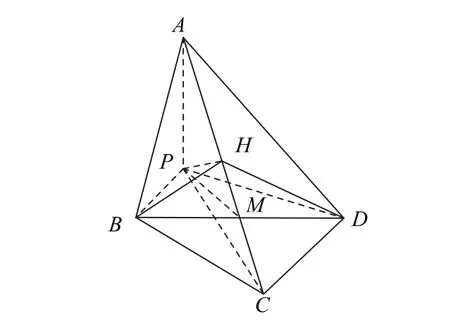
图1

因为∠APB＝90°＝∠APD,所以AP⊥平面PBD,从而AP⊥BD,故BD⊥平 面PAC,则 平 面PAC⊥平面ABCD.作PH⊥平面ABCD于H,则点H在交线AC上.又AP⊥PM,所以点H在线段AM上.记∠PCA＝α,由PB＝PD＝2＝CB＝CD,M是线段BD的中点,可得MP＝MC,则∠CPM＝α,故∠AMP＝2α.在Rt△PAM与等腰△MPC中,有

再由Rt△PAH,得

故选A.

分析图形几何性质,合理安排垂足位置,增强空间图形的直观性,便于几何计算,扎实的空间想象能力和平面几何分析能力是基础.

例2 (北京大学)在△ABC中,AC＝1,BC＝3,AB＝2,M为线段AB的中点,把△BCM沿CM折起,使得三棱锥B′-ACM的体积为,则A,B′两点之间的距离可以是( ).

先作出图2～5,依次体现原图到最后折叠图形.其中图2与图3分别是原图及其直观图,图4 与图5 是折叠后的两种图形,分别对应二面角B′-CM-A为钝二面角、锐二面角两种情形.

图2

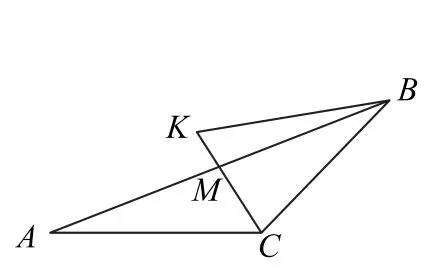
图3

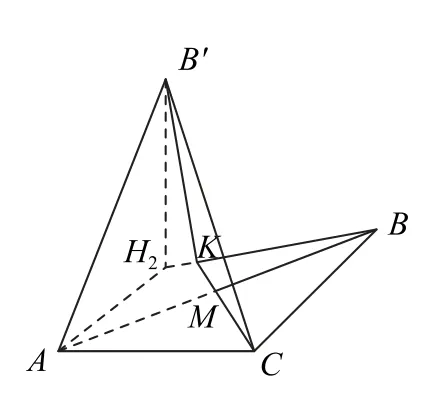
图5

因为△ACM的面积,所以三棱锥B′-ACM的高为

情形1 二面角B′-CM-A为钝二面角,如图4所

在图4中,由△ABH1,应用余弦定理,得

再在图4中,由Rt△AH1B′,应用勾股定理,得

情形2 二面角B′-CM-A为锐二面角,如图5所示,作B′H2⊥平面ACM于H2,则垂足H2位于线段BK延长线上.以下计算参考情形1,得AB′＝2.

综上,选BC.

折叠问题中的几何作图,需分析清楚折叠过程中的垂直关系、位置关系与不变性,弄清折叠前后图形的关联,从而合理地利用折叠前的平面图形理解折叠后的空间图形,并完成相关计算.

2 求几何体中的角

2.1 内容提要

空间角包括如下5种类型,如表2所示.

表2

求空间角需要合理作出角,其中“合理”是为了作直观的图形,将问题转化到一个平面上,最后应用余弦定理或锐角三角形函数求一个三角形的内角问题.

2.2 典例精析

例3 (清华大学)四面体D-ABC顶点处三个角∠BDC,∠CDA,∠ADB的 大 小 分 别 是arctan2,则二面角B-AD-C的大小为_________.

如图6所示,在棱DA上取一定点O,在平面DAB与平面DAC上分别过点O作AD的垂线,交DB,DC于M,N,则∠MON就是二面角B-AD-C的平面角.

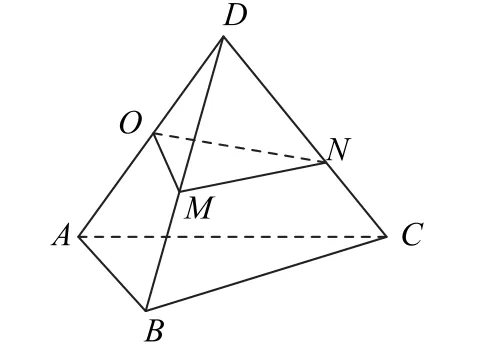
图6

记OD＝a,在Rt△DOM中,∠DOM＝90°,∠MDO＝arctan2,因此

同理,在Rt△DON中,ON＝3a,DN＝2a.

在Rt△MDN中,由勾股定理,得

在△MON中,由余弦定理,得

所求二面角的平面角大小θ的余弦值可以用三射线定理直接写出:

例4 (北京大学)在三棱锥P-ABC中,∠BAC＝90°,PA⊥平面ABC,如果PA＝AB＋AC,求∠APB＋∠APC＋∠CPB.

如图7所示,在平面APB上作AM⊥PB于M,连接CM.因为PA⊥平面ABC,∠BAC＝90°,所以平面PAB⊥平面ABC,且交线为AB.再由AC⊥AB,可得AC⊥平面PAB,从而PB⊥AC,故PB⊥平面AMC,CM⊥PB,所以

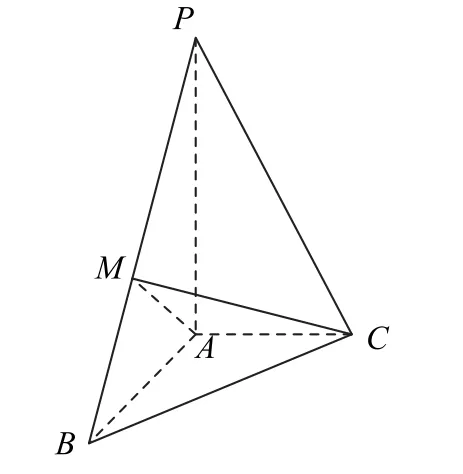
图7

另一方面,有

由①②,可得

再由PA＝AB＋AC＞AB和AC,可 知∠APB＋∠APC＜45°＋45°＝90°,从而

即

本题解析思路基于熟知的三余弦公式:

例5 (清华大学)已知正三棱柱ABC-A1B1C1的9条棱长都相等,在棱AB上有一点P满足平面PB1C1、平面PA1C1与平面A1B1C1所成角分别为α,β.

(2)求tan(α＋β)的最小值.

如图8所示,在平面A1ABB1上,作PM⊥A1B1于M,则PM⊥平面A1B1C1.

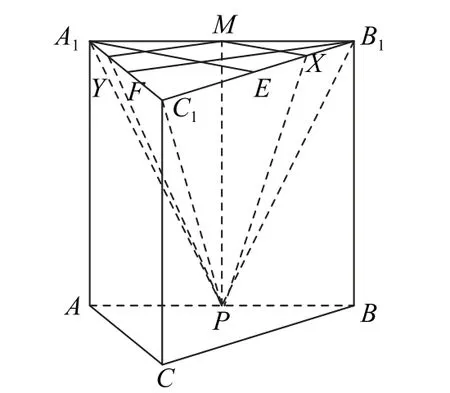
图8

分别取线段B1C1,A1C1的中点E,F,则A1E⊥B1C1,B1F⊥A1C1.再分别取线段B1E,A1F的中点X,Y,则MX//A1E,MY//B1F,所以MX⊥B1C1,MY⊥A1C1,故二面角P-B1C1-A1的平面角为∠PXM＝α,二 面 角P-A1C1-B1的 平 面 角 为∠PYM＝β.

因为正三棱柱ABC-A1B1C1的9 条棱长都相等,所以可设其长为1.(1)记AP＝x∈(0,1),则BP＝1－x,A1M＝x;,所以MY＝.在Rt△PMY中,有

通过推理转化,把求几何最值归结为探究一个代数最值,应注重对目标式子调结构,寻求应用均值不等式快捷确定最值的结构.

3 求几何体的面积与体积

3.1 内容提要

几何体中的面积计算主要包括侧面积、全面积与截面面积;体积的算法比较灵活,包括著名的“等积变换”.梳理柱体、锥体与球体的体积公式,如表3所示.

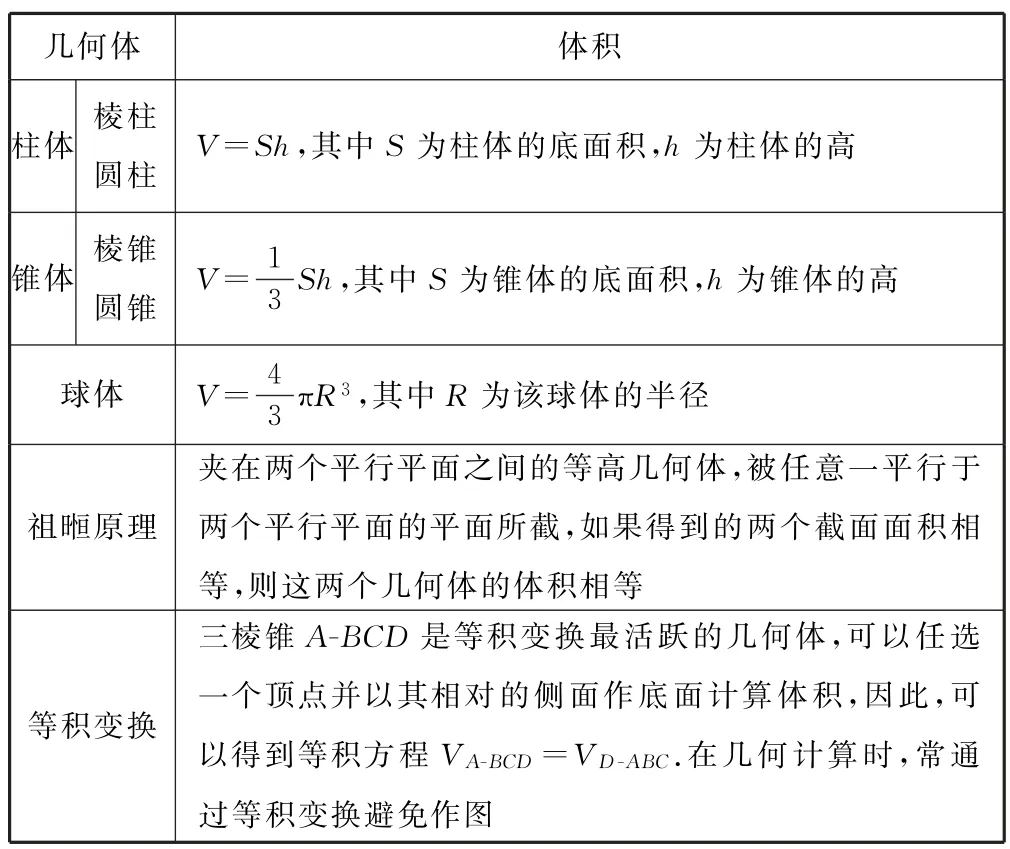
表3

表4

探求几何体的体积时要合理选择体积公式,并在题设几何情境中寻求公式所需几何量的计算路径,其中作出几何体的高及计算其长度往往是解题难点.

3.2 典例精析

例6 (北京大学)在三棱锥D-ABC中,AC＝BC＝AD＝BD＝1,则三棱锥D-ABC的体积V的最大值为( ).

如 图9 所 示,线 段AB,CD的中点分别记作E,F,分别作长度为h的向量,使线段CD,A′B′互 相 平 分,则 四 边 形A′DB′C是平行四边形.因为

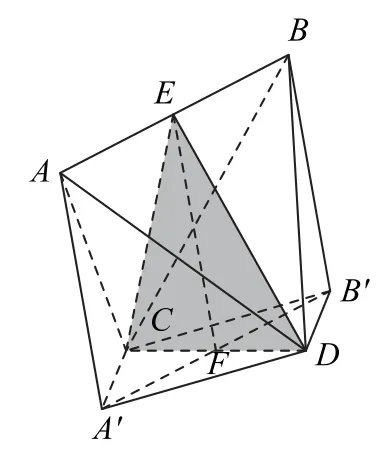
图9

所以△CAB≌△DAB,从 而EC＝ED,并且ED⊥AB,EC⊥AB,则AB⊥平面ECD,故AB⊥CD.再由A′B′//AB,得A′B′⊥CD,平行四边形A′DB′C是菱形.记(AB,CD,AA′)＝(2x,2y,h),则.由EC＝ED,FC＝FD,可得EF⊥CD,结合EF⊥A′B′,且CD∩A′B′＝F,得EF⊥平面A′DB′C,进而AA′⊥平面A′DB′C,∠AA′D＝90°,故

例7 (北京大学)在圆锥MO中,M是顶点,O是底面圆心,点A在底面圆周上,点B在底面圆内,MA＝6,∠ABO＝90°,OH⊥MB于H,C为母线AB的中点.当四面体O-CHM的体积最大时,线段BH的长度是( ).

如图10 所示,引入OM＝x,OB＝y,AB＝z,由OM⊥平面OAB,∠ABO＝90°,可得x2＋y2＋z2＝OM2＋OB2＋AB2＝MA2＝36.因 为AB⊥OB,AB⊥OM,所以AB⊥平面OBM,故OH⊥AB.

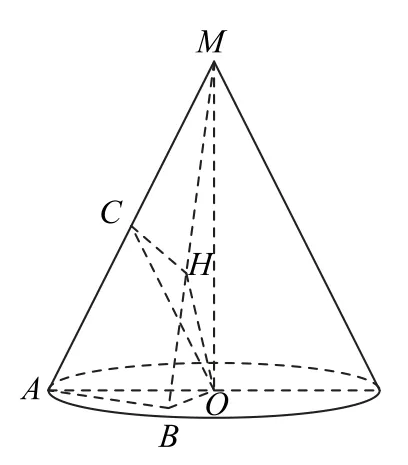
图10

等号成立的条件是

故选D.

得到条件x2＋y2＋z2＝36(x＞0,y＞0,z＞0),也可进行球变换:

将原问题转化为三角函数求最值问题.

4 球与球面关联的几何计算

4.1 内容提要

4.2 典例精析

例8 球O的直径SC＝4,A,B为球面上两点,满足AB＝3,并且∠ASC＝∠BSC＝30°,则四面体S-ABC的体积V＝________.

如图11所示,取弦AB的中点M,连接MC,MS.由题设可知CS是球O的直径,则∠CAS＝90°＝∠CBS,又∠ASC＝30°＝∠BSC,从而CA＝CB＝2,SA＝SB＝2 3,所 以AB⊥MC,AB⊥MS,故AB⊥平面CMS.在△CMS中,有

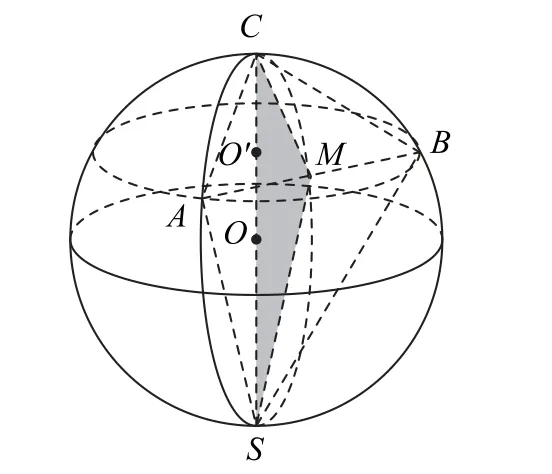
图11

由余弦定理,得

所以

例9 (中国科技大学)将地球视作半径为R的球体,则分别位于东经120°北纬60°和西经120°南纬60°的A,B两地之间的球面距离是_________.

“球面距离”是指过球面上两点的大圆上的劣弧AB的长度L,因此,应先计算球心角∠AOB的弧度数,为此要先求出线段AB的长度.

由题设可知A,B两点的地理坐标分别是A(120°,60°),B(－120°,－60°).如图12 所示,取点A′(－120°,60°),B′(120°,－60°),则60°北纬线就是图中过A,A′的小圆O1,60°南纬线就是图中过B,B′的小圆O2,东经120°经线就是过A,B′的大圆O,西经120°经线就是过A′B的大圆O.

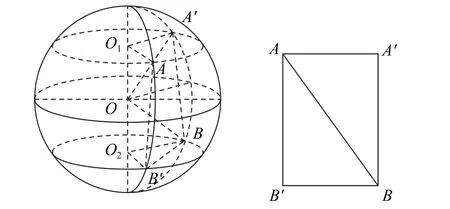
图12

5 探求空间轨迹

空间曲线是满足某种运动条件的动点的运动轨迹,命题立意通常包括判断曲线的类型.

例10 (北京大学)用一个平面α,截一高为h且底面圆的半径为r的圆柱面,得到一椭圆曲线,并且椭圆与圆柱的底面恰有一个公共点,则沿柱面展开的交线形状为________.

如图13所示,在截口线上任取一点P,作PM⊥圆O′所在平面于M,则M在底面圆周上.记平面α与圆O′所在平面的交线为l,则l与底面圆O′相切于点O.在底面圆O′所在平面上作MN⊥l于N,则Rt△PMN∽Rt△A′AO,所以

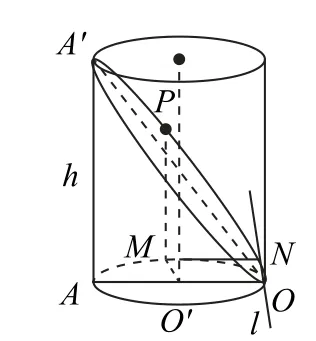
图13

记∠OO′M＝θ∈[0,2π],圆O′的半径为r,则沿逆时针方向弧OM的长度为x＝rθ.

另一方面,记PM＝y,AA′＝h,AO＝2r,则MN＝r－rcosθ,代入①,得

因此,把截面交线铺展在平面上所得曲线即为点P(x,y)的轨迹,其参数方程为

消去参数θ,得,故交线形状为一段余弦曲线.

6 基于三视图构建直观图计算求解

三视图是检测学生空间想象能力,培育学生情境转化能力,锻炼和发展学生几何分析、几何推理和几何计算能力的最佳题材.

例11 (清华大学)已知一个四棱锥的三视图如图14所示,则该四棱锥的四个侧面中,直角三角形的个数是________.

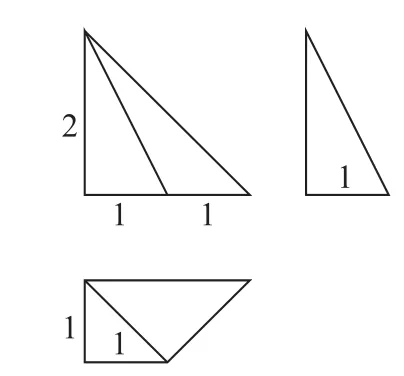
图14

如图15所示,在棱长为2的正方体ABCDA′B′C′D′中,取棱AD的中点E,底面中心O,则三视图表示的几何体在图15 中即为四棱锥D′-OCDE.

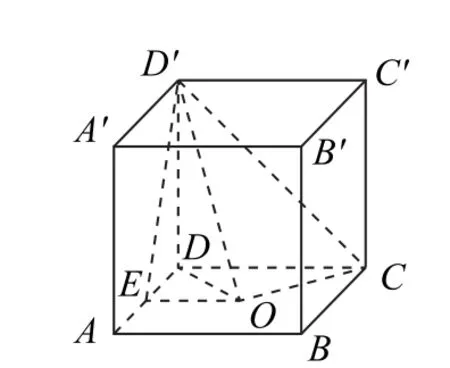
图15

由DD′⊥平面ABCD,可知∠D′DC＝90°＝∠D′DE,则△D′DC与△D′DE都是直角三角形.再由OE⊥AD,OE⊥DD′,可得△D′EO是直角三角形.

因为∠COD＝90°,所以OC⊥OD,且DD′⊥OC,所以OC⊥平面ODD′,故∠COD′＝90°,则△OCD′是直角三角形.

综上,题设四棱锥的四个侧面都是直角三角形,故直角三角形的个数是4.

通常可先在一个正方体中构建出三视图表现的几何体,再计算路径.

7 求解新概念问题

基于几何情境抽象,提出新概念,检测理解能力、空间想象能力以及应用概念进行几何推理与计算的能力.

例12 (清华大学)对于三维空间中任意给定的空间四边形ABCD,四条线段AB,BC,CD,DA顺次首尾相连,定义顶点A的内角为射线AB和射线AD所成角,其补角称为顶点A的外角,其他顶点的定义相同.若空间四边形ABCD的外角和为X,则( ).

A.X＝2π

B.X≥2π

C.X≤2π

D.X相对于2π的大小关系不确定,三种可能性都存在

记空间四边形ABCD各顶点的所有内角和为Y.一方面,按题设定义,得

另一方面,如图16 所示,由∠ABC≤ ∠ABD＋ ∠CBD,∠ADC≤∠ADB＋∠CDB,得

图16

由①和②,得X≥2π,故选B.

例13 (北京大学)设定点A,B,C,D是以点O为中心的正四面体的顶点,用σ表示空间内以直线OA为轴,满足条件σ(B)＝C的旋转;用τ表示空间内关于平面OCD的镜面反射;设l为过棱AB中点与棱CD中点的直线,用ω表示空间内以l为轴,作180°的旋转变换.定义σ∗τ为一个复合变换:σ∗τ(P)＝σ(τ(P)),即先作变换τ,再作变换σ,则ω可表示为( ).

A.σ∗τ∗σ∗τ∗σB.σ∗τ∗σ∗τ∗σ∗τ

C.τ∗σ∗τ∗σ∗τD.σ∗τ∗σ∗σ∗τ∗σ

如图17所示,直线l分别过棱AB,CD的中点M,N,由MC＝MD以及NA＝NB,可知直线l是异面直线AB,CD的公垂线,并且垂直平分线段AB,CD,所以ω(A,B,C,D)＝(B,A,D,C).

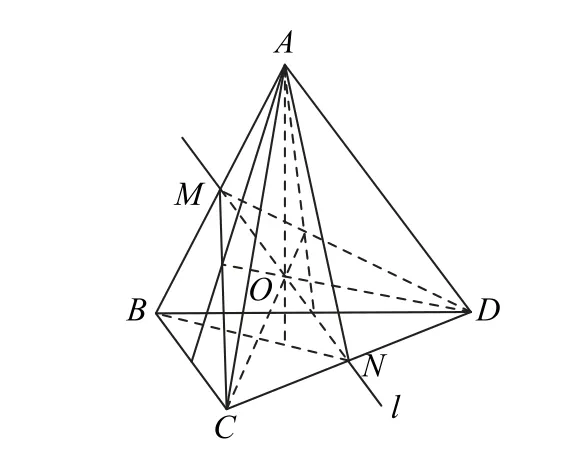
图17

因为平面OCD就是平面MCD,所以τ(A,B,C,D)＝(B,A,C,D).再根据变换σ的定义,得σ(A,B,C,D)＝(A,C,D,B).因为

所以选项A,B,C都不正确,因此D 是正确选项.

事实上,有

综上,选D.

(完)