如何利用等体积法求点线面的距离

温德俊

(四川省威远县竞力学校)

等体积法是空间几何中常用的一种求距离的方法,它可以求出点与线、点与面、线与面之间的距离.当我们遇到与点线面有关的距离问题时,可以考虑将一个空间几何图形换个方向投影,然后通过体积的不同表示方法求出相应的距离.等体积法较为简单,不需要对图形进行复杂的分割和计算,但是在转化方面稍有难度.

1 求定点到面的距离

例1 如图1 所示,正方体ABCD-A1B1C1D1的棱长为2,E是棱CC1的中点,则点C1到平面EBD的距离为( ).

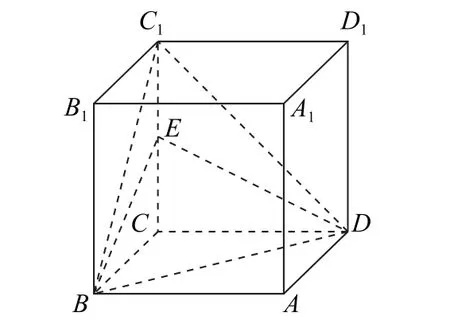
图1

因为正方体ABCD-A1B1C1D1的棱长为2,E是棱CC1的中点,所以

设点C1到平面EBD的距离为h,则VC1-EBD＝VB-C1ED,所以

该题为基础题,类似于平面几何三角形中的利用等面积法求高,体积等于底面积乘高,在高不好求的情况下,可尝试将该三棱锥换个底面,然后通过等体积法进行求解.

2 求动点到面的距离

例2 如图2所示,在三棱锥P-ABC中,PA＝PB＝PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,且CE⊥EF,若M为三棱锥PABC外接球上的动点,则点M到平面ABC距离的最大值为_________.

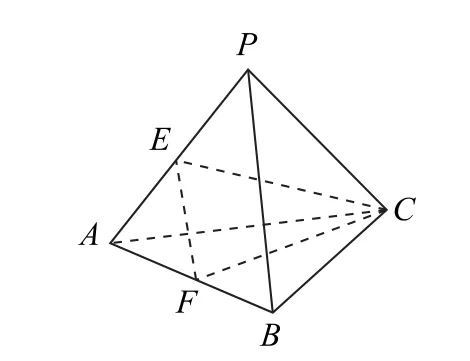
图2

可以先证得PB⊥平面PAC,再求得PA＝PB＝PC＝2,从而可知P-ABC为正方体的一部分(如图3),正方体的体对角线即为球的直径,从而使问题获解.

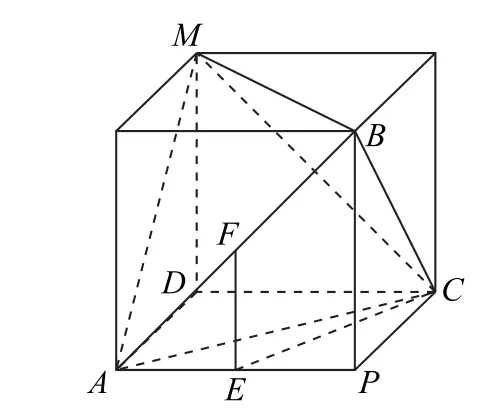
图3

因为PA＝PB＝PC,△ABC是边长为2的等边三角形,故P-ABC为正三棱锥,PB⊥AC.又E,F分别为PA,AB的中点,故EF//PB,所以EF⊥AC,又EF⊥CE,CE∩AC＝C,因此EF⊥平面PAC,PB⊥平面PAC,则∠APB＝90°,所以

又M为三棱锥P-ABC外接球上的动点,所以当M位于正方体的顶点(如图3)时,点M到平面ABC的距离最大,设最大距离为h,则三棱锥M-ABC的体积为

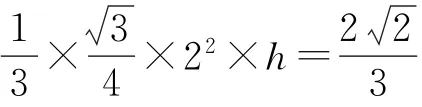
该题难点在于P-ABC外接球的构建需要较强的空间想象力.在外接球的构建过程中,正方体(或长方体)这类的特殊几何体可以作为中介,可先将三棱锥置于正方体(或长方体)内,如此,便可在正方体(或长方体)的空间内进行求解,将来无论是利用体积公式,还是建立空间直角坐标系,都将更加容易.

3 求直线到面的距离

例3 如 图4 所 示,AD//BC且AD＝2BC,AD⊥CD,EG//AD且EG＝AD,CD//FG且CD＝2FG,DG⊥平面ABCD,DA＝DC＝DG＝2.

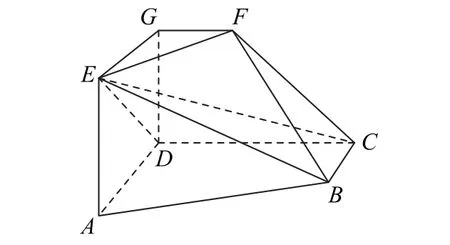
图4

(1)求平面EBC与平面EFG的夹角;

(2)求直线AD到平面EBC的距离.

本题可通过建立空间直角坐标系求解第(1)问,第(2)问可以利用等体积法进行求解.

(1)因为AD⊥CD,DG⊥平面ABCD,故以D为 坐标原 点,DA,DC,DG分 别 为x轴、y轴、z轴 建立空间直角坐标系,如图5所示.

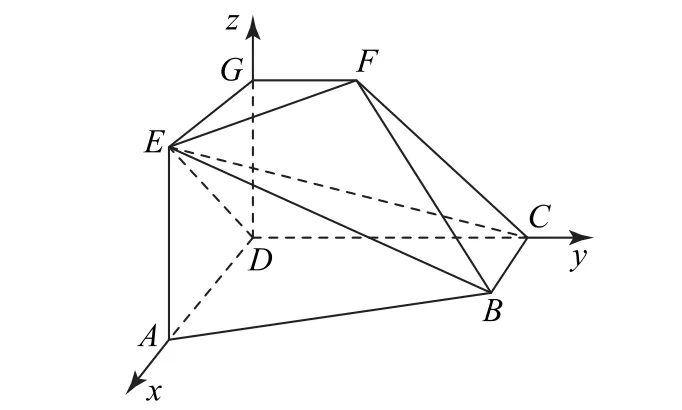
图5

由题可知D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),易知平面EFG的一个法向量为,设平面EBC的一个法向量为

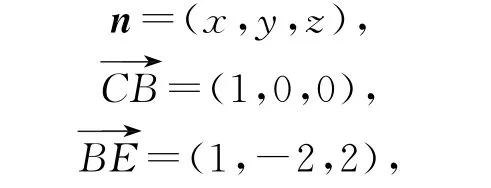
所以平面EBC与平面EFG的夹角为45°.

(2)因为AD//BC,BC⊂平面BCE,则AD//平面BCE,所以直线AD到平面EBC的距离与点D到平面EBC的距离相等.

如图6所示,连接CG,BD,由(1)可知AD⊥平面CDGF,所以AD⊥CG.

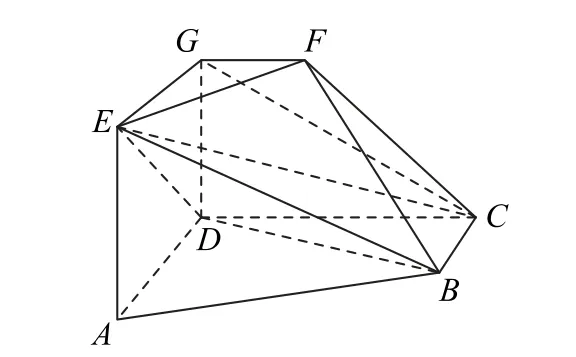
图6

又BC//AD,所以BC⊥CG,设点D到平面EBC的距离为h,则

又VD-BCE＝VE-BCD,所以,解得h＝2,所以直线AD到平面EBC的距离为2.

本题既考查了向量计算,又考查了等体积转化的方法.尤其在第(2)问中,既可以直接建立空间直角坐标系进行向量计算,又可以通过巧妙的等体积法进行体积公式的转化和表示.求直线到平面的距离,隐含着直线与平面平行的条件,因此实际上是考查直线上的点到平面的距离,通过等体积转化可以巧妙求解.

(完)