化归与转化思想在立体几何问题中的应用

李洪伟

(山东省青岛西海岸新区第二高级中学)

化归与转化思想是高中数学中的重要思想方法,对学生数学学习有着重要的意义.立体几何是高中数学的重要内容,要求学生具备较强的直观想象、数学运算以及逻辑推理能力,同时立体几何也是高考数学中的重要考点.本文分析化归与转化思想在高中立体几何问题中的应用策略.

1 化陌生为熟悉,简化空间图形解题

在高中数学立体几何问题中,一些题目对于学生来说较为陌生,此时可以利用化归与转化思想将陌生问题转化成熟悉问题,再借助学生熟悉的解题方式对问题进行全面分析,提高学生学习效果与解题效率.

例1 在一个直径为10的球体中有一个圆台,圆台上底面的半径是4,下底面的半径是5,求圆台的体积.

如图1 所示,设圆球的球心为O,圆台上底面的圆心为O1,圆台经过OO1的截面是梯形ABCD,延长AD,BC与OO1,相交于点S,则△SAB为等腰三角形,O是AB的中点.根据题目条件,可以得出CO1＝4,BO＝5.因为△SO1C∽△SOB,所 以.连接OC,在Rt△OO1C中,由勾股定理可得OO1＝3,所以,解得SO1＝12,SO＝15,所以圆台体积

此题考查圆台与球的切接问题,先求出底面与球的关系,之后利用几何关系将圆台体积转化成大圆锥与小圆锥的体积差,进而完成问题的解答.

2 化三维为二维,借助平面图形解题

高中数学立体几何问题对学生空间想象能力要求比较高,在实际的解题中,教师可以引导学生将立体问题平面化处理,帮助学生分析立体问题,有效解答立体几何问题.

例2 如图2所示,ABCDA1B1C1D1是 长 方 体,AB＝AD＝1,AA1＝2,M是棱DD1上任意一点,当A1M＋MC取最小值时,证明:B1M⊥平面MAC.

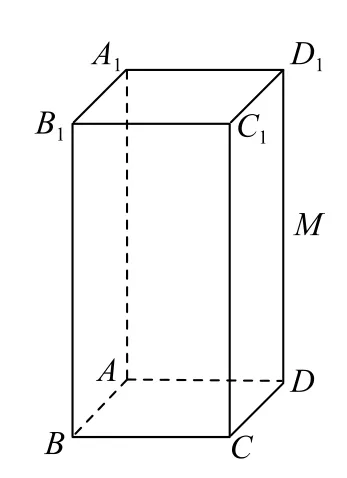
图2

如图3 所示,将侧面CDD1C1围 绕DD1旋转90°,使得其与侧面ADD1A1在同一平面,当A1,M,C′三点共线时,A1M＋MC的值最小.因为AB＝AD＝1,AA1＝2,所以M是DD1的中点.因为C1M＝MC＝2,C1C＝2,利用勾股定理可以得出C1C2＝C1M2＋MC2,则∠C1MC＝90°,所以C1M⊥CM.因为B1C1⊥平面CDD1C1,所以B1C1⊥CM,因为B1C1∩C1M＝C1,所以CM⊥平面B1C1M,则CM⊥B1M,同理可证B1M⊥AM,又AM∩CM＝M,所以B1M⊥平面MAC.

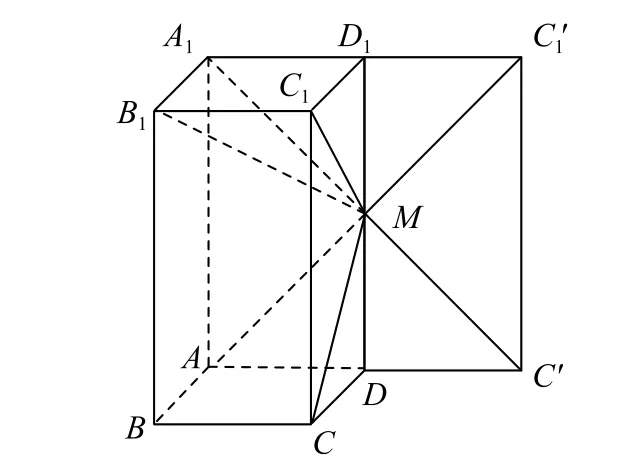
图3

在立体几何问题中,空间位置关系可以通过平面图形处理,如异面直线形成的角、二面角以及线面角等可以进行相应的转化,解题时需明确平面图形关系,通过转化完成问题的解答.

3 化几何为代数,利用向量知识解题

数形转化思想是高中数学的重要思想方法,在解答代数问题时,常常会将数转化成形,利用图形解答问题.在立体几何解题中,借助化归与转化思想将几何问题转化成代数问题,通过计算解答几何问题.

例3 如图4 所示,在长方体ABCD-A1B1C1D1中,底 面ABCD为正方形,在棱AA1上有一个点E,且BE⊥EC1.

图4

(1) 证 明:BE⊥ 平面EB1C1;

(2)若AE＝A1E,求二面角B-EC-C1的正弦值.

(1)因为ABCD-A1B1C1D1是长方体,所以C1B1⊥平 面ABB1A1.因 为BE在 平 面ABB1A1上,所 以BE⊥B1C1.又BE⊥EC1,EC1∩B1C1＝C1,所以BE⊥平面EB1C1.

(2)以B点 为 原 点,分 别 为x轴、y轴、z轴,建立空间直角坐标系,如图5所示.设AB＝a,BB1＝2b,则B(0,0,0),C(a,0,0),C1(a,0,2b),E(0,a,b).

图5

在空间几何问题中,若线线角、线面角以及二面角难以直接求解时,可以通过构建空间直角坐标系,将几何问题转化成代数问题.

4 化无形为有形,借助模型解答问题

在高中数学中,有很多复杂、抽象的问题.面对这样的问题,如果学生无法有效提炼信息,则难以找到解题思路,此时可以通过化归与转化思想将无形转化成有形,借助模型分析和解答问题.

例4 如图6所示,在三棱锥P-ABC中,AP⊥平 面ABC,∠ACB＝90°,AC＝BC＝1,AP＝3,则三棱锥P-ABC外接球的体积为____.

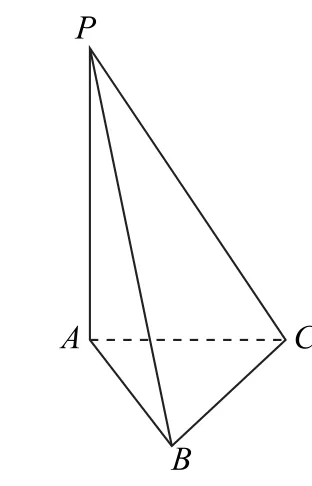
图6

方法2 如图7 所示,根据题意,对三棱锥进行补形,补成一个长为1、宽为1、高为3的长方体,则三棱锥的外接球与长方体的外接球是同一个球.设外接球的半径是R,所以所以,从而该三棱锥外接球的体积为

图7

此题是求解三棱锥外接球体积的典型例题,方法1是常规解法,通过分析几何图形特征,确定外接球的球心,进而求解出外接球的半径,完成体积求解.方法2是利用补形法,将无形转化成有形,通过对几何图形的结构特点进行分析,将三棱锥补形得到长方体,根据长方体的结构特点,求解外接球半径,简化解题过程,提高立体几何解题效率.

(完)