空间几何体最值问题解题策略探究

梁琪雅

(福建省厦门双十中学)

空间几何体最值问题是高中数学的常考问题,该类问题情境复杂多变,解题方法灵活多样.求解问题时需具体问题具体分析,采用针对性策略,寻找切入点.实践表明,解答空间几何体最值问题常用方法主要有基本不等式法、空间向量法、二次函数法、导数法等,本文举例分析.

1 基本不等式法

基本不等式法是求解空间几何体最值问题的常用方法.运用该方法解题的关键在于灵活运用题干中的已知条件,合理设出相关参数,构建相关参数之间的关系.在构建参数之间的关系时注重灵活运用几何知识(如勾股定理、三角形相似等)探寻未知参数.

例1 在三棱锥P-ABC中,点P在底面上的射影O为△ABC的垂心,如图1 所示,其中AO的延长线交BC于点D.S△ABC•S△OBC＝S2△PBC,若△PAB,△PBC,△PAC的面积之和的最大值为8,则三棱锥P-ABC外接球的体积为________.

由题意可知PO⊥BC,而AD⊥BC,PO∩AD＝O,则BC⊥平面PAD,则BC⊥PD,BC⊥AP.由S△ABC•S△OBC＝S2△PBC,可得

整理得AD•OD＝PD2,即,而∠ODP＝∠PDA,则△ODP∽△PDA,∠POD＝∠APD＝90°,所以AP⊥PD.又BC∩PD＝D,故AP⊥平面PBC,则AP⊥PB,AP⊥PC.同理,得BP⊥PC,即PA,PB,PC两两垂直.设PA,PB,PC的长分别为a,b,c,则

2 空间向量法

空间向量是研究空间几何体的重要工具,尤其用于解决动点问题,可能会获得事半功倍的效果.运用向量法解答空间几何体最值问题应建立能够便于运算的空间直角坐标系.同时,运用题干中线段的等量关系,借助坐标运算确定动点轨迹,而后运用立体几何知识,通过转换分析问题的视角,迅速找到解题的切入点.

例2 已知正方体ABCD-A1B1C1D1的底面ABCD内存在一动点P,且满足|PA|＝2|PB|.设PD1 和平面ABCD 所成角为α,则α 的最大值为_________.

动点问题应首先想到运用空间向量法分析.以点B为原点,分别以BC,BA,BB1所在直线 为x轴、y轴、z轴 建立空间直角坐标系,如图2所示.设正方体的棱长为2,点P(x,y,z),则A(0,2,0),D(2,2,0),由|PA|＝2|PB|,得

图2

3 二次函数法

二次函数是学生非常熟悉的函数.求解空间几何体最值问题有时运用二次函数可获得良好效果.当然构建二次函数应建立在对空间几何体点、线、面空间位置的准确判断与把握上,因此,应灵活应用线线平行、线面平行、面面平行以及垂直判定定理.

例3 如图3所示,正方体ABCD-A1B1C1D1的棱长为2,点P1,P2分别在线段AB,BD1(不含端点)上运动,且P1P2//平面A1ADD1, 则 四 面 体P1P2AB1 的体积的最大值为_____.

图3

4 导数法

求解空间几何体最值问题有时构建的函数较为特殊,为顺利解答需运用导数知识判断特殊函数的单调性求出其最值.构建函数时要注重运用空间几何体基础知识,基于空间几何体面积、体积公式构建函数.为更好地突破问题,深化学生的认识与理解,实践中可借助多媒体技术多视角展示空间几何体,更好地把握空间几何体之间的关系,在头脑中留下深刻的印象.

例4 如图4所示,四棱锥P-ABCD的底面是边长为2 的正方形,PA⊥底面ABCD,且PA＝2.若在该四棱锥中挖掉一个体积最大的圆柱,则该圆柱体的体积为_________.

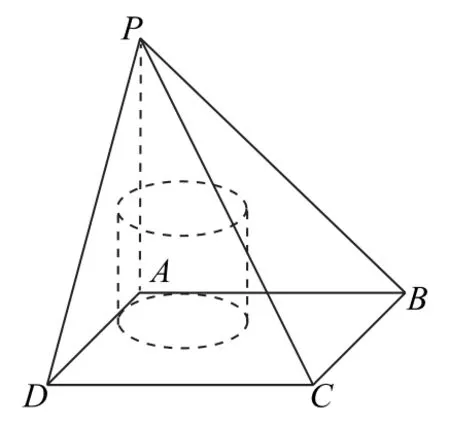
图4

综上,解决空间几何体最值问题时应具备灵活的思维,掌握通法通解,同时,应把握不同解题方法的特点以及适用题型,多进行训练与反思,及时发现与弥补解题中的不足,实现解题能力的进一步提升,从而在以后解题时把握关键点,迅速找到解题切入点,避免走弯路.

链接练习

1.已知三棱锥P-ABC中,PA⊥平面ABC,AB＝2,△ABC和△PAB的外接圆圆心分别为O1,O2,若该三棱锥外接球的表面积 为16π,设O1A＝a,O2A＝b,则a＋b的 最 大 值为_________.

2.在正方体ABCD-A1B1C1D1中,|AB|＝3,点E为线段AB上靠近点A的三等分点,在△A1BD内有一动点P(包括边界),则|PA|＋|PE|的最小值为_________.

3.已知四棱锥P-ABCD内接于半径为1的球,则该正四棱锥体积最大时,高为_________.

4.在正方体ABCD-A1B1C1D1中,侧面ADD1A1上存在一动点P,且PB1⊥A1C,则直线PB1和直线AB所成角的正弦值的最小值为_________.

链接练习参考答案

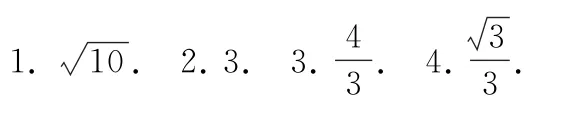
(完)