源于教材 凸显素养——一道立体几何模拟试题的命制与思考

刘 臻 喻瑞明

(1.江西省南昌市第二中学 2.江西省南昌市第一中学)

笔者多次参与了模拟试题的命制工作,对试题的命制有一些思考,现以一道立体几何模拟试题为例,探析考查学生数学学科核心素养试题的命题思路.试题命制灵感源于教材,却高于教材,极具创新性,凸显数学学科核心素养.本文将试题的命制与思考过程整理成文,与各位读者分享.

1 试题呈现

引例 如图1 所示,在直三棱柱ABC-A1B1C1中,AB＝AC＝2,AA1＝1,AB⊥AC,点E,E1分别是棱BC,B1C1的中点,点G在棱A1B1上,且GB1＝2,截 面AA1E1E内 的 动 点P满 足GB⊥PE1,则PE＋PB1的最小值是( ).

分析 这是一道以三棱柱为背景的立体几何题,在考查立体几何核心知识的同时,凸显探究意识,考查学生的逻辑推理、直观想象等数学核心素养.

2 命题立意

命题时既要立足教材,又要适度提高,既要注重基础知识的应用,又要有一定的创新性,指向数学核心素养的考查.立体几何试题考查的核心是借助几何直观,将空间几何问题转化为平面几何问题,把握图形之间的关系,揭示数学问题的本质,对提升学生的直观想象、数学抽象与逻辑推理等数学核心素养大有帮助.因此,以简单、熟悉的几何体为背景,以动态问题为载体,考查立体几何问题的平面化思想.

3 命制历程

3.1 基于教材,初次尝试

例1 (北师大版数学必修第二册第115页的例2)图2是古希腊数学家特埃特图斯(Theaeteus,约前417—前369)用来构造无理数2,3,5,…的图形.试计算图中线段BD的长度及∠DAB的大小(长度精确到0.1,角度精确到1°).

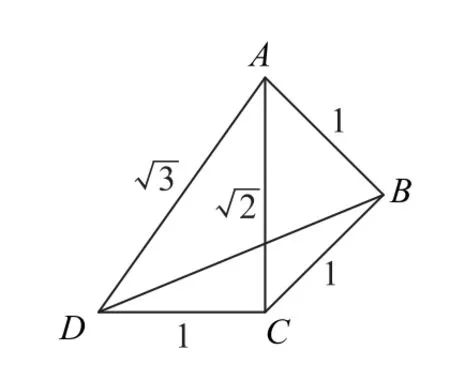
图2

这是一道可以运用余弦定理求解的平面几何问题,我们将△ABC沿着AC折叠,就可以将平面几何问题转化为立体几何问题,于是将例1改编为例2.

例2 如图3所示,在三棱锥A-BCD中,AB＝AC＝CD＝1,AB⊥AC,DC⊥CB,点P在线段BC上运动,则BP＋PD的 最 小 值为_________.

图3

考虑到上述问题比较常见,立体几何模型过于直接,因此尝试将三棱锥隐藏到三棱柱中,如图4所示.

图4

3.2 线面关系,动态探究

若把注意力放在几何体中的线面关系,则结合线面的平行关系可将例2改编为例3,结合线面的垂直关系可将例2改编为例4.

例3 如图5所示,在直三棱柱ABE-CFD中,AB⊥AE,AB＝AE＝BF＝1,G,H分别为BE,DF的中点,点P在四边形ABFC内运动,若HP//平面ADG,则AP＋PD的最小值为________.

图5

例4 如图6 所示,在直三棱柱ABE-CFD中,AB⊥AE,AB＝AE＝BF＝1,点P在四边形ABFC内 运 动,若PF⊥DB,则BP＋PE的最小值为_________.

图6

例3和例4是可行的,不见波澜、中规中矩,但稍作思考总感觉例2和例3略显平庸,“味道”不够,那么该怎么改呢?

3.3 隐藏探究,降维变换

例3和例4的创新度稍微欠缺,如果能在几何体中增加一些探究就可谓更上一层楼了.此时笔者突发闪念,若能将立体几何模型的“探索”元素进一步隐藏,那就可谓是锦上添花了.

例5 如图7所示,在三棱柱ABC-A1B1C1中,AB＝BC＝AA1＝1,AB⊥BC,D,E分别为A1B1,A1C1的中点,点P在三棱柱ABC-A1B1C1内,若AD⊥EP,则A1P＋PC的最小值为_________.

图7

在本题的基础上,增设棱的长度和相应的角度,依托线面垂直进行探究,这样就渗透了空间问题平面化的思想,既体现了化归与转化思想的考查,也增加了命题的新颖性,吸引、激发考生解题的兴致,于是确定了最后的定稿.

4 试题解析

解 如图8 所示,过点G作GM//BC交A1C1于点M,交A1E1于点H,连接MC,EH,因为BC⊥平面AA1E1E,截面AA1E1E内的动点P满足GB⊥PE1,所以EH⊥PE1.

图8

如图9所示,经计算可知四边形EE1HN为正方形,则点P在线段E1N上(E1除外).如图10所示,进一步探究PE＋B1P的最小值,只需将△ENE1沿着E1N折叠,使得△ENE1与平面B1E1N在同一个平面.如图11所示,连接B1E交NE1于点P,点P即为满足题意的点,此时,经计算可知PE＋PB1的最小值为5,故选C.

图9

在解答立体几何问题时,要先从几何体的结构特征出发,增强对几何体“形”的判断和识别能力,即“形定而后动”,再结合已掌握的解题思想进行深入分析,把化归与转化及数形结合的思想运用得淋漓尽致.

5 命题思考

命题实践是一项具有创新意义的活动,不仅能加强数学教学的针对性,科学合理地检测学生学习的状况和水平,更是能促进教师专业发展的有效路径.

教师应潜心钻研教材,充分挖掘教材中习题和例题的潜在功能,基于教材进行原创试题命制,有利于拓展学生的数学思维.在教学与评价中,要关注学生对具体内容的掌握,更要关注学生数学学科核心素养水平的表现.因此,数学题的命制既要基于基础知识,尊重教材,又要突破、创新,凸显数学学科核心素养.

(完)