对一道高考试题的再探究
安徽省泗县第二中学 于先锋 (邮编:234300)
2008年安徽省高考数学试题理科第22题为:
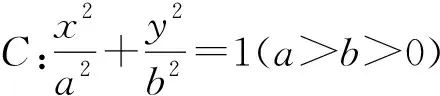
(Ⅰ)求椭圆C的方程;

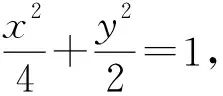
探究一若椭圆退化为圆,则点Q是否在某定直线上?
不失一般性,设点P(a,b)在圆C外,圆C的方程为:x2+y2=r2.
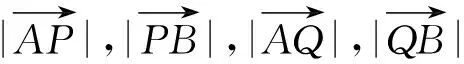

图1


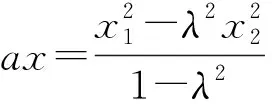
①
②
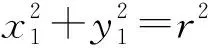
③
④
①+②并结合③,④,可得直线ax+by=r2,这是我们非常熟悉的一条直线,即过点P(a,b)向圆C所作切线得两个切点的连线(切点弦所在的直线).


探究二当点P(a,b)在椭圆C:Ax2+By2=C(A>0,B>0)外时,相应的结论是否还成立.
利用探究一的方法可得点Q在定直线Aax+Bby=C上,下面证明此直线就是过点P向椭圆C作切线的两个切点的连线.
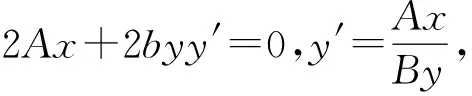

图2
⑤
又点M在椭圆上,即Ax32+By32=C
⑥
由⑤、⑥得Aax3+Bby3=C
⑦
同理,由过点N的切线为Aax4+Bby4=C
⑧
由⑦、⑧得,过两切点M、N的直线是Aax+Bby=C,证毕.

对于方程Ax2+By2=C(C≠0),若AB<0,则它表示的曲线是双曲线,因此上述结论对双曲线也成立,那么该结论对抛物线是不是成立呢?
探究三设点P(a,b)与抛物线C:y2=2px(p>0),点P在y轴左侧,那么相应的结论是否还成立
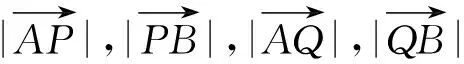
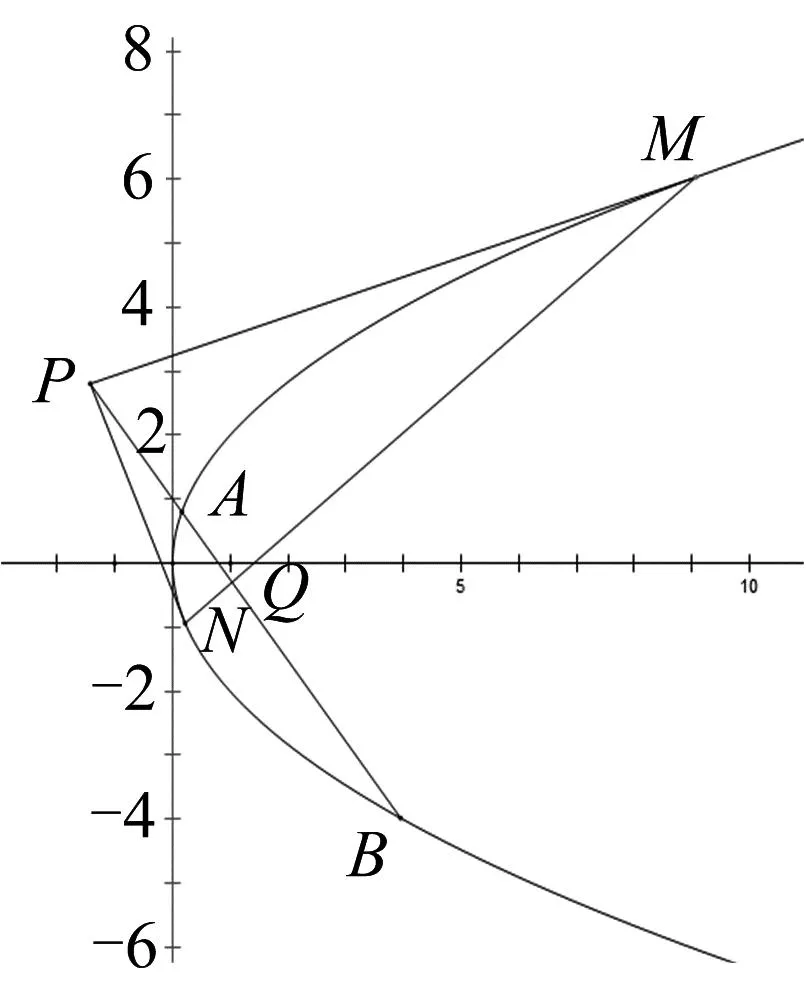
图3

⑨
⑩
据A(x1,y1),B(x2,y2)在抛物线C上,并将⑨、⑩分别代入C的方程y2=2px(p>0),整理可得(b+λy)2=2p(a+λx)(1+λ)
(b-λy)2=2p(a-λx)(1-λ)
因为λ≠0,所以by=p(x+a),即点Q总在直线by=p(x+a)上.可以证明此直线是过点P向抛物线C所作切线的两个切点的连线.
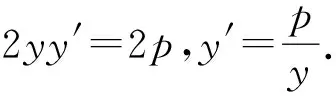

又点M抛物线C上,所以y32=2px3
同理,由过点N的切线为by4=p(a+x4)


在上述定理中,若点P在线段AB上,点Q在线段AB延长线上,其它条件不变,点Q还在一条定直线上吗?若是,它又是怎样的一条直线?下面以椭圆为例进行探究.
设点P(a,b)在椭圆C:Ax2+By2=C(A>0,B>0,C≠0)内.利用探究一的方法,同理可得点Q在定直线Aax+Bby=C上.
下面探究直线Aax+Bby=C的位置.
如图4,以点P为中点作圆锥曲线C的弦MN,过M、N作圆锥曲线C的切线交于点E,过点E作弦MN的平行线EF,下面证明平行线EF的方程是Aax+Bby=C.
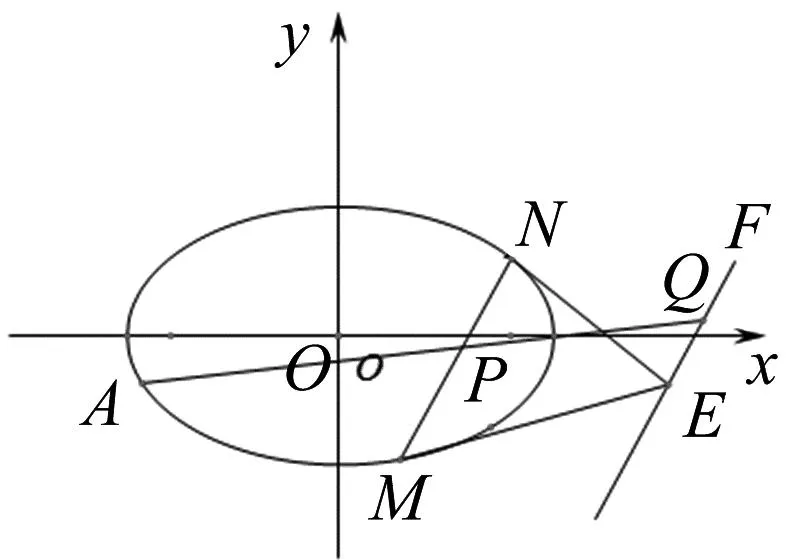
图4
设A、B、E的坐标分别为(x1,y1)、(x2,y2)、(p,q),
由A、B都在椭圆上可以得到:
当x1≠x2时,由得
又因为P是MN的中点,所以x1+x2=2a,y1+y2=2b
过M、N作椭圆C的切线交于点E,也可以认为过点E向C作切线,切点为M、N,则直线MN的方程可以用点P的坐标表示为:Apx+Bqy=C
当x1=x2时,点P在x轴上(不在坐标原点),则直线EF的方程Aax=C也满足Aax+Bby=C,对于圆、双曲线、抛物线,也可以用上述方法证明.


探究四当点P(a,b)是椭圆C:Ax2+By2=C(A>0,B>0)外一点时,定理1的逆定理是否成立?
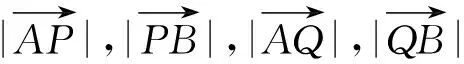

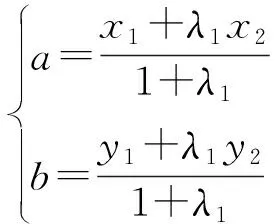
由前面知过切点M、N的直线l的方程是Aax+Bby=C
点Q在直线l上,其坐标满足方程,将代入得:
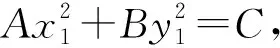

当A=B时,Ax2+By2=C(A>0,B>0,C>0)表示圆.
当AB<0时,Ax2+By2=C(C>0)表示表示双曲线.
因此,上述结论对圆、双曲线也成立.
可以用相同的方法推导上述结论对抛物线也是成立的,请读者自行完成.

以上通过类比的思想和方法,主要探究了圆锥曲线中的定直线问题、比例问题,这些都值得回味和深思.

