等边三角形旋转下的两个优美恒等式及延申
安徽省寿县第一中学 梁昌金 (邮编:232200)
1 两个优美恒等式
问题1如图1,将等边三角形△ABC任意旋转一个方向后得△DEF,AB与DE,DF交于点G,H,BC与DF,EF交于点M,N,CA与EF,DE交于点K,L,则
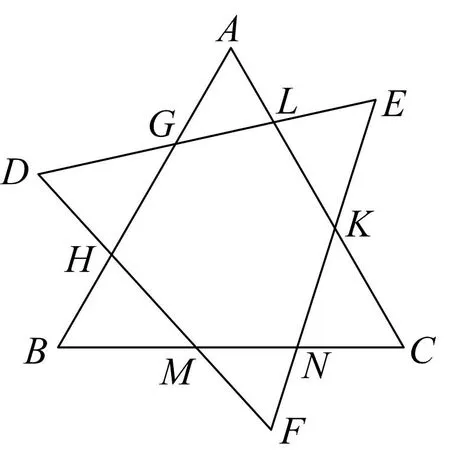
图1
(1)GL2+HM2+NK2=KL2+GH2+MN2;
(2)GL+HM+NK=KL+GH+MN.
证明(1)由条件△ABC≌△DEF,
又S△ABC-S六边形GHMNKL=S△AGL+S△BMH+S△CNK,
S△DEF-S六边形GMLKIH=S△DGH+S△FMN+S△EKL,
所以S△AGL+S△BMH+S△CNK=S△DGH+S△FMN+S△EKL.
易知△AGL∽△DGH∽△BMH∽△FMN∽△CKN∽△EKL,
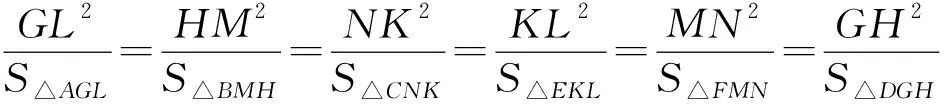
①
所以
从而GL2+HM2+NK2=KL2+GH2+MN2.
(2)设GL+HM+NK=x,KL+GH+MN=y,AB=DE=a.
因为△EKL∽△AGL,
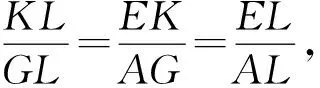
因为△FMN∽△AGL,
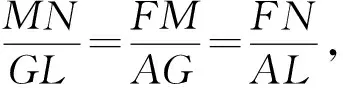
因为△DGH∽△AGL,
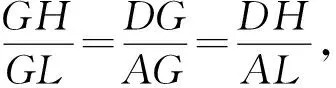

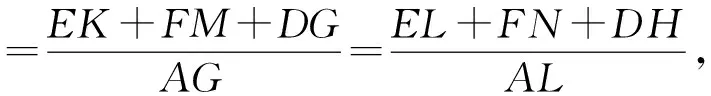
②
由△EKL∽△CKN,△FMN∽△CKN,△DGH∽△CKN,同理得
③
由△EKL∽△BMH,△FMN∽△BMH,△DGH∽△BMH,同理得
④
由②③④得
所以x(3a-x)=y(3a-y),则(x-y)(x+y-3a)=0,
又x=GL+HM+NK<(AG+AL)+(BM+BH)+(CK+CN),所以
x+y<(AG+GH+BH)+(BM+MN+CN)+(CK+KL+AL)=3a,
所以x=y,即GL+HM+NK=KL+GH+MN.
2 两个推论
条件同问题1,得到:
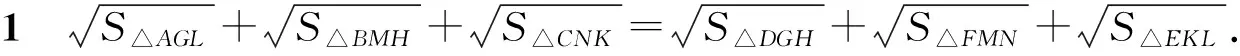
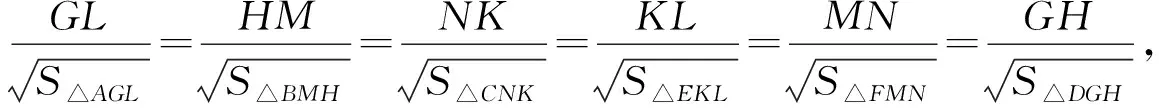
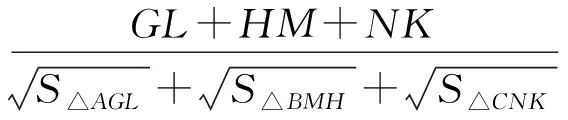
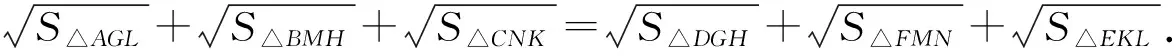
推论2GL·HM+HM·NK+NK·GL=KL·MN+MN·GH+GH·KL.
简证由问题1,知GL2+HM2+NK2=KL2+MN2+GH2,GL+HM+NK=KL+MN+GH.
则(GL+HM+NK)2-(GL2+HM2+NK2)=(KL+MN+GH)2-(KL2+MN2+GH2),
整理即得GL·HM+HM·NK+NK·GL=KL·MN+MN·GH+GH·KL.
3 “褪去”特征,由等到不等
等边三角形、全等是△ABC,△DEF的特征,“褪去”这个特征,笔者得到下面优美不等式.
问题2如图2,已知I是△ABC的内心,AI,BI,CI分别交△ABC外接圆于点F,E,D,AB与DE,DF交于点G,H,BC与DF,EF交于点M,N,CA与EF,DE交于点K,L.

图2
求证HG+LK+NM≥GL+KN+MH.
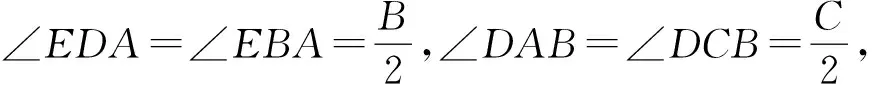

因此△AGL是等腰三角形,AI垂直平分GL,设AI和GL交于点P.
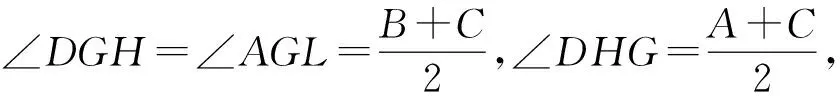
由△DQG∽△APG,得
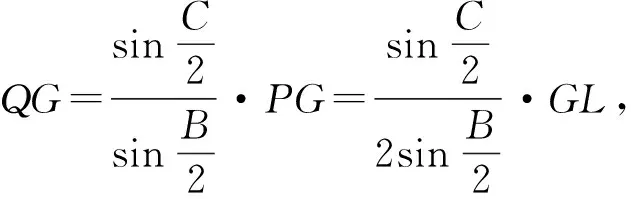
所以HG=QG+QH
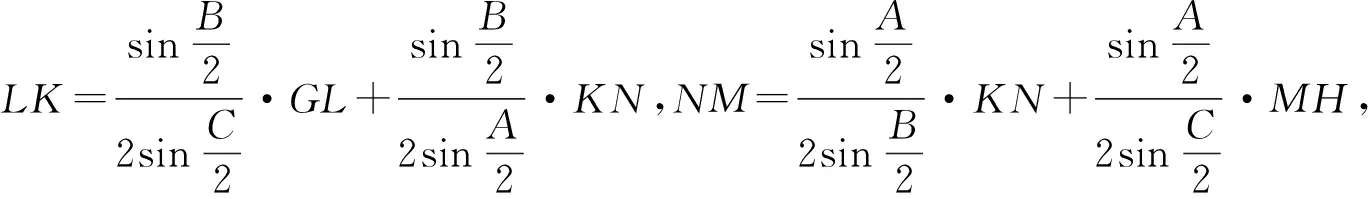
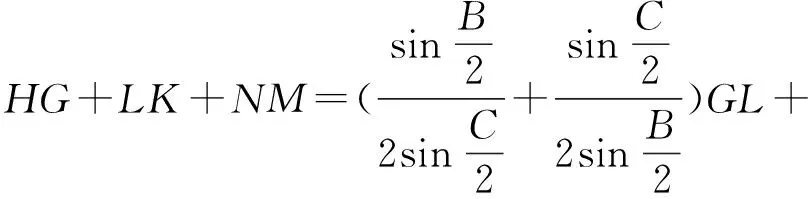
通过研讨发现△DEF对比△ABC是一种递增的三角形序列(面积增加、周长增加),这是否是问题2结论的本质?对于三角形重心、垂心、外心按相同的方式生成的△DEF是否有类似于问题2的结论,留给有兴趣的读者继续研讨.

