基于UbD理论的高中数学逆向教学设计——以“随机事件与概率”单元为例

吉林师范大学数学与计算机学院(四平校区) 杨艳秋 (邮编:136000)

吉林师范大学数学与计算机学院(长春校区) 王跃涵 (邮编:130000)

1 引言

UbD(Understanding by Design)理论是美国教育学家Grant Wiggins和Jay McTighe在20世纪90年代提出的一种追求理解的教学设计模式,意为“理解为导向的教学设计”主张教学应该始于教育的最终目标[1]. 目前我国对于UbD理论的研究也日渐丰富,其中吴华和隋红梅基于UbD理论的逆向教学设计框架对初中概率初步进行研究[2]. 李保勤和陈雪梅将STEM课程和UbD理论进行融合,构造了指向素养和理解的教学设计LS-UbD模型,并对概率论中帕斯卡和费马的骰子实验进行案例研究[3]. 无论是吴华和隋红梅,还是李保勤和陈雪梅,都对概率相关内容进行了逆向教学设计的案例研究,足以见得概率模块在教学中的重要性.但目前为止还未有专家针对高中概率模块进行逆向教学设计的案例研究,而高中概率的教学有助于培养学生辩证思维,其中“随机事件与概率”作为概率模块的开篇单元为后续几何概型、事件的相互独立性以及概率与频率的学习奠定基础.基于UbD理论中的大概念、基本问题、理解六侧面、WHERETO元素对人教版高中数学课标教材(A版)必修第二册“10.1随机事件与概率”单元进行逆向教学设计案例研究.

2 UbD理论概述与逆向教学设计

2.1 大概念

大概念(big ideas)也被称为核心概念是学科的核心,具有内在的可迁移特性,将离散的主题和技能联结起来[4]. 与学科知识要掌握更加具体的知识相较,大概念的知识范围更广它与单元相结合突破了主题的界限,激发了学习者的探索欲望并帮助学生对知识进行联系形成相关的知识脉络,但大概念不是一味的大和抽象,过于抽象的概念不利于学生的理解,因此教育者在教学过程中,应该根据所学习的内容切合实际的选择大概念. 其中UbD理论中将大概念作为预期教学目标设定的核心,也是基本问题提出的前提,例如在“随机事件与概率”这一单元中,从知识和技能出发,思考“随机事件与概率”当中所蕴含的数学思想再进一步凝结成“概率意义与运算”这一大概念.

2.2 基本问题

以问题为基础的教学能够促进学生发现知识之间的联系,促进思维的发展,让学生在问题中学到知识,又能够灵活运用、迁移知识. 基于问题的教学已经成为教学改革后的一条新路径,作为培养学生的高阶思维和学科核心素养的重要方法. 基本问题实际上就是包含了核心大概念的学科核心知识,也是在学习核心知识时必须要解决的问题. 它使得学生能够参与到各种各样的高阶思维中以增强学习能力[5],同时能够为后续的学习奠定基础. 基本问题的特征就是通过提出令人深思的、值得探讨的问题,促进高阶思维的发展从而提高学生的学习能力. 如图1,UbD理论将基本问题作为设定预期目标的核心框架,通过一系列基本问题来筛选出值得深度思考的问题.

2.3 理解六侧面

在信息高速发展的今天,计算机和人工智能已经取代了大部分识记性工作,因此能够拥有对于核心问题的完美的理解力正是我们社会所需要的、创新性人才所追寻的,也就是说理解是信息时代学习的核心价值,也是能够有效学习的核心条件[6]. 与其他学科相比数学更加抽象注重逻辑,那么在数学学科的教学设计中更应该注重学生是否真正理解、是否能够将知识进行迁移并能够应用到实际的问题中去,进而促进学生的学科核心素养落实,那么如何评估“理解”呢?如何确定学生真实的理解程度呢?UbD理论将理解分为六个维度,并将其作为评估学生理解程度的依据包括:能解释、能阐明、能应用、能洞察、能神入、能自知[5],并可将这六个维度分为三个层次,分别为:叙述(能解释、能阐明)、运用(能应用、能洞察)、发展(能神入、能自知),如表1.

表1 理解六侧面的含义

2.4 WHERETO元素

为了教育者能够设计出有助于学习者理解核心知识、对问题深入思考、灵活运用和迁移知识,从而促进学习者高阶思维发展的教学设计. 教育学家Grant Wiggins和Jay McTighe等人归纳出了教学设计的七要素,即WHERETO元素,帮助教育者将预期目标、确定的评估证据贯通在具体教学中[7]. 每个元素的意义如表2.

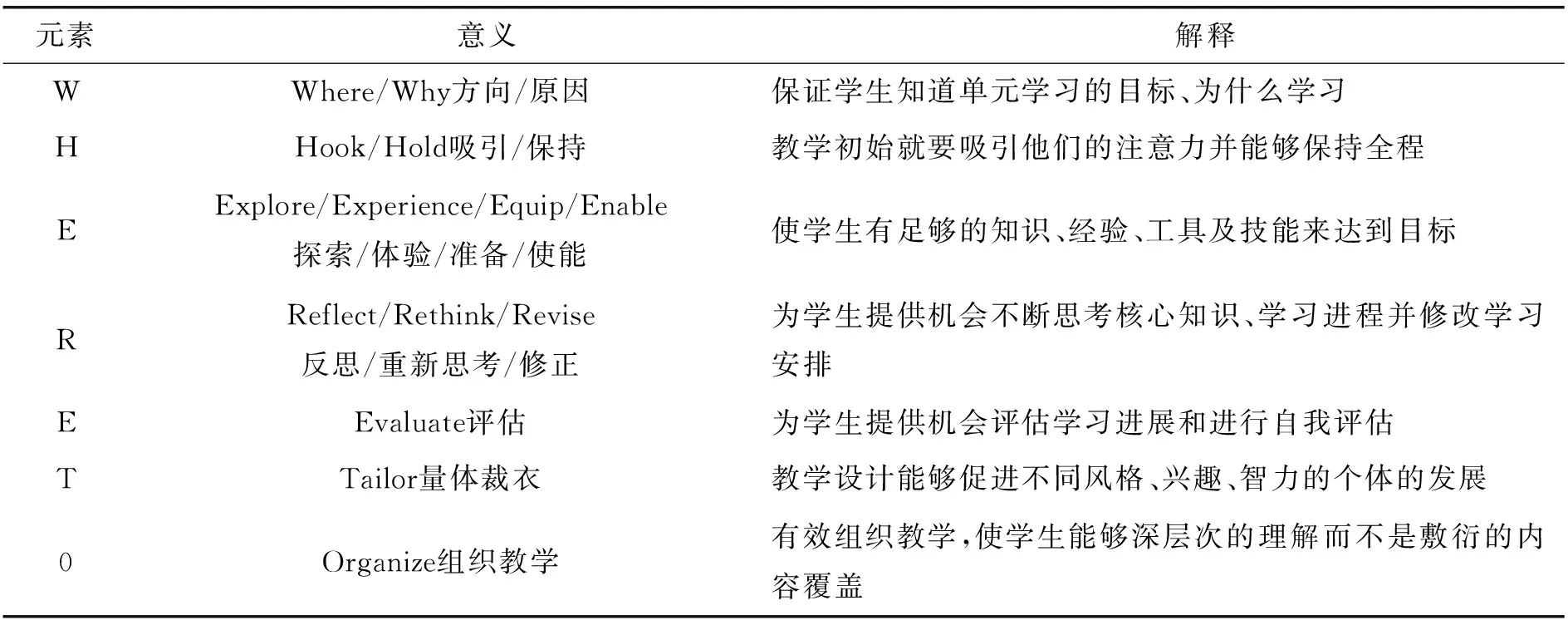
表2 WHERETO元素及其意义

2.5 UbD理论与逆向教学设计的联系

逆向教学设计包括三个阶段:确定预期目标—确定评估证据—进行教学设计. 第一阶段:确定预期目标,这一阶段教育者需要根据《普通高中数学课程标准(2017年版2020年修订)》、学情、教材围绕基本问题筛查出本节课需要理解的核心任务,明确教学重点,要知道学生在本节课应该理解什么、学生将会知道什么、学生在这节课的学习后能做到什么?第二阶段:确定评估证据,这一阶段教育者应该明确用什么来证明学生真正理解了学习的内容,收集学生达成目标的评估证据. UbD理论运用理解六侧面来评估学生理解的层次,只能够对核心知识进行解释、转述,说明学生处于理解的浅层次阶段也就是理解六侧面的叙述层次,能够对核心内容完全理解处于理解六侧面的应用层次,而有的学习者能够运用各种高阶思维进行思考已经达到发展的层次. 第三阶段:进行教学设计,在这一阶段要根据预期的教学目标和确定的评估证据来设计教学框架,并思考用什么方法、如何进行教学活动来达到预期的理解.UbD理论借助WHERETO元素对教学设计进行优化,后续的学习计划将以WHERETO中的元素设计具体的教学活动,并将第一阶段中的基本问题和第二阶段的评估证据进行梳理,使其能够得到实践,前两个阶段的理论为最终教学设计中WHERETO元素渗透入整个教学过程提供了理论基础. 最后,大概念是整个逆向教学设计的核心,它贯穿于三个阶段之中并与基本问题、理解六侧面、WHERETO四者处于一个不断循环交织的过程,如图2.

图2 UbD理论下逆向教学设计的基本流程

3 UbD理论下“随机事件与概率”的教学设计

根据UbD理论的概述和基本步骤的分析,UbD理论比传统教学更可以加强学生对于核心知识的理解. 下面根据UbD理论中阶段1——确定预期结果,阶段2——确定评估证据,阶段3——进行教学设计的框架设计顺序对“随机事件与概率”单元的逆向教学设计进行探索.

3.1 阶段1——确定预期目标

“随机事件与概率”这一单元内容从“随机事件”展开,包含随机事件的可能性大小的认识,事件的关系和运算,概率的基本性质等部分内容,基于《数学课程标准》中相关内容可将本单元教学的大概念确定为“概率意义与运算”. 利用基本问题筛选流程思考下面问题:为什么学习“随机事件与概率”这一单元,该单元的研究价值是什么,想让学生在这一单元学到什么,达到什么样的理解程度[8]. 教学中期望学生能够阐述为什么要学习“随机事件与概率”,能够达到“概率意义的理解”,能够“计算随机事件的概率并解决实际问题”. 基于以上分析将《数学课程标准》中确定的教学目标以及需要掌握的知能,并结合基本问题与预期的理解构成了确定预期目标的设计框架,如表3.

表3 阶段1——确定预期目标

3.2 阶段2——确定评估证据

在这一阶段需要教育者找到足够的评估证据来考查学生理解的程度,基于理解六侧面确定和评估“随机事件与概率”的理解证据评价如下:

(1)能够解释“随机事件与概率”单元中相关概念的含义——能理解、能阐明;

(2)能求解实际问题中古典概型的概率,并能够根据具体题目灵活运用概率运算法则——能应用、能洞察;

(3)能理解问题核心思想找到隐含条件,能够在足够多的练习和解决问题的过程中清楚自己的不足并能够进行修正——能神入、能自知.

在对“随机事件与概率”单元进行教学评价时不能只注重终结性评价,需要形成性评价来发现教学中出现的问题并及时调整. 评估中的依据可以来自于课堂的观察与问答、随堂测验、单元测试、自我评价:

(1)观察与问答——通过课堂上学生的表现以及提问来考查学生对概念的理解;

(2)随堂测验——学完一小节的内容后对学生进行测试,考查学生对于该部分知识的应用与迁移情况;

(3)单元测验——考查学生对本单元核心知识的理解程度;

(4)自我评价——在单元结束时,评估课后作业以及练习题的完成情况;反思在随机事件相关概念、事件之间关系上的理解不足;反思在运用古典概型公式和概率运算法则进行计算时的思路.

3.3 阶段3——进行教学设计

教师在教学设计当中以“概率的意义和运算”为核心,将基本问题、确定评估证据以及相关的零碎的知识点进行链接,使学生在本单元的学习中能够对“概率的意义和运算”形成完整的知识结构. 针对教与学的顺序并结合WHERETO元素列出本单元的学习和教学活动,如表4.

表4 阶段3——“随机事件与概率”的逆向教学设计

在这一阶段,教育者要明确本单元要达到的预期结果以及如何高效的安排教学过程. 那么本阶段主要设计思路如下:通过回顾初中概率知识引入本单元的内容,明确本单元要学什么,以及为什么学?;通过师生探讨和学生对于问题的思考让学生形成知识逻辑结构;让学生寻找生活中相关的实例形成问题,探索解决问题的方法,并形成解决问题的一般思路,培养学生的批判性思维和学科核心素养的发展.

4 结论启示

基于 UbD 理论的逆向教学设计是实际可操作的,并不只是停留在理论.它以终为始先确定预期目标再结合预期的评估证据来进行教学设计,解决了传统教学中学生对于大概念的理解浅薄的问题,而大概念与学科核心素养有潜在的联系,因此概念的理解促进了学科核心素养的落实.大概念、基本问题、理解六侧面、 WHERETO 元素为逆向教学设计提供了坚固的理论基础,使其可以在实际教学中稳扎稳打的实行.UbD理论下的逆向教学设计始终围绕着大概念进行,这样的教学设计可以更加明确课堂的核心任务,使学生更加清晰掌握学习的方向.