大概念视域下的章节起始课研究——以《数列的概念与简单表示》为例

江苏省溧水高级中学 李宽珍 (邮编:211200)

1 问题的提出

章节起始课,是指每一章教学内容的第一节课.大概念视域下的章节起始课要基于数学的逻辑系统思考,需要整体设计.大概念教学注重概念产生的情境,更注重学生已有的数学认知.因此,基于大概念下的数学教学,一方面,教师要对整个知识体系、整章知识结构了如指掌,进而才能对新概念做好“解构”,即对知识进行选择和重组,使之更贴合学生已有的认知水平;另一方面,借助利于概念所依托的情境,引导学生经历知识的形成,从而更好的渗透数学思想,真正完成学生个体对知识体系的构建.

下面以苏教版选择性必修一第四章第1课时“数列的概念与简单表示”的为例,具体阐述如何在大概念下设计和实施教学.

2 学情分析

数列是苏教版选择性必修一第四章的内容,涉及的知识点有数列的定义,数列的项,通项公式及数列的表示,数列的分类等概念.本章是学生在学习了集合、函数、三角函数等知识后的内容,学生对新知识的研究已有一定的方法和“研究套路”.因此,本课通过大量的情境让学生获得概念的初体验,抽象出数列的概念;根据学生在前面学习函数时积累的知识结构,在问题的引导下,能尝试去观察、分析、猜想和证明.通过类比,得到研究数列的知识体系,让学生勾勒出研究新事物的一般框架.在新知识的形成过程中帮助学生最终相对独立地去完成数列的建构活动,培养了学生的数学核心素养——数学抽象,直观想象,逻辑思维.

3 教学过程

活动一创设情境场 明示课题

情境1古希腊数学家毕达哥拉斯研究过的数学问题,他们提出的一组数:1,3,6,10,… 这些数可以用三角形点阵表示,故称其为三角形数.

(1)1,3, 6,10,…

情境2“一尺之棰,日取其半,万世不竭”,剩余棰长问题:

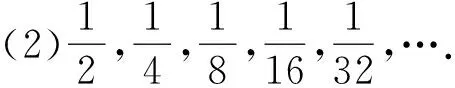
情境3剧场座位数问题:

(3)20,22,24,26,…,78.

情境4我国从1984年后参加的8次奥运会获得的金牌数:

(4)15,5,16,16,28,32,51,38.

问题1通过以上情境,我们可以得到哪些数组?

生1:根据以上情境,我们可以得到如下几列数:

(1)三角形数依次为:1,3, 6,10,…

(3)座位数依次为:20,22,24,26,28,…,78

(4)金牌数依次为:15,5,16,16,28,32,51,38.

问题2以上情境中有什么共同特点?又各有什么特点?

生2:以上情境都是数,按照一定的顺序排列.

设计意图根据几个情境,创设一定的情境场,引导学生体验引入数列概念的“必要性”.情境1和2是传统的数学史引入案例,先通过展示古希腊毕达哥拉斯学派的数学家的三角形数和《九章算术》中的例子,使得数学课也有了文史色彩．情境3和4来自实际生活中的案例,这两类案例意在告诉学生数列问题不仅是一个历史悠久的问题,而且是身边常见的现象.这些例子其实也是数学建模的典型案例,对学生今后数学建模思想的形成会起到不可忽视的作用.四个实际问题,说明数列模型在现实生活中大量存在,告诉我们学习数列的必要性,同时四个实例也涉及到了本章要学习的等差数列、等比数列核心的知识,使得研究的数列问题已经有了一定的思维高度．

活动二师生互动,建构新知

师:说的很好!我们把这种按一定次序排列的一列数叫做数列. 你能举出一些数列吗?

(学生举例)

师:再看下面两组案例:

(1)①场地上堆放了一批钢管, 从上往下数有4,5,6,7,8,9,10;

②场地上堆放了一批钢管, 从下往上数有10,9,8,7,6,5,4.

这两个数列是不是同一个数列呢?为什么?

生3:不是同一个数列,因为顺序不一样.

师:恩,很好!再看下面的数列呢?

(2)某人2022年1～12月的工资,按月顺序排列为:4800,4800,4800,…,4800 .这一列数是数列吗? 与其他数列有何不同?

生4:也是数列,这个数列中的每个数都相同.

师:很好!你能用不同的标准给下列数列分类吗?

(1)1,3, 6,10,…

(2)20,22,24,26,28,…,78

(4)15,5,16,16,28,32,51,38.

(5)15,5,16,16,28,32,51,38,…

(6)5000,5000,5000,…,5000

(7)4,5,6,7,8

生5:可以通过项数和项两个标准来进行分类,若根据数列项数的多少,可分为有穷数列和无穷数列.根据项的大小来看,又可分为递增数列、递减数列、常数列和摆动数列.

师:你能用不同的标准对问题情境中引入的数列进行分类吗?

(学生按照刚才的标准对情境中的数列进行分类.)

师:数列中的每一个数叫做这个数列的项.各项依次叫做这个数列的第n项,数列的一般形式可以写成:a1,a2,a3,…,an,…,或简记为{an}.

活动三类比迁移,渗透方法

问题3数列中的每一项与其序号之间是怎样的关系?

生6:数列的项和序号是一一对应的,也就是说对于每一个正整数n,都有惟一的数an与之对应.

问题4这个概念是否似曾相识?你能从函数的角度解释数列吗?

生7:和函数的定义类似,对于定义域中的每一个自变量x,都有唯一的y与之对应.

师:那数列的自变量是什么?定义域是什么?函数值和值域又是什么?

生8:类比函数,数列可以看成定义域为孤立整点的函数,此函数的值域即为数列.

师:我们是按照什么样的思路研究函数的?

生9:是按照函数的背景——函数的概念——函数的性质——特殊函数——函数应用的顺序研究的.

师:数列是一种特殊的函数,你觉得数列的研究路径是什么?

生10:可以类比数列,按照数列的现实背景——数列的概念——数列的性质——特殊数列——数列应用这样的过程研究数列.

活动四巩固概念,反馈矫正

师:既然大家知道可以类比函数来研究数列,现在给出数列:

(1)1,3,6, 10,…

(2)20,22,24,26,28,…,78

(3)2,4,8,16,32,64,128,…

问题5你能用一个式子表示数列吗?你认为数列可以用哪些方法表示?为什么?

生11:可以用第n项an与n之间的关系来表示.

师:很好!这就是数列的通项公式.即第n项an与n之间的关系,可以表示成an=f(n).类比函数,数列也有三种常用表示方法:(1)列表法;(2)通项公式法;(3)图象法.

设计意图类比函数的研究方法得到数列的研究过程,渗透数学中类比的数学思想.通过类比促使学生更好的认识数学的整体性,将所学的数学知识、方法结构化、系统化,串成一个完整的体系．在运用、研究某个概念时,其本质上是重启、唤醒概念所属的知识体系．因此,教学概念时,应以本概念的系统结构为基础,从学生已有的知识体系出发,引导学生感知新旧概念的关联,探究概念建构的内涵与外延,从而新概念逐步融入到学生已有概念网络体系中去．

活动五质疑答辩,运用新知

师:运用新知识解决下列问题:

例1已知数列{an} 的通项公式,写出数列的前5项,并作出它的图象.

例2写出数列的一个通项公式,使它的前4项分别是下列各数:

设计意图通过例1的教学让学生先写前几项,再画图象,再次体验函数的研究方法.通过动手操作体会数列是特殊的函数．通过例2写通项公式,再次体验求函数解析式的思想.通过例题的教学,渗透函数的思想,数形结合思想和类比的思想等.

活动六归纳整理,整体认识

师:通过本节课的学习你有什么收获?

生12:从知识上看,学习了数列的概念、分类方法、数列的表示,数列的本质和研究思路等.

从数学思想方法上看,有数形结合、分类讨论、类比思想等数学思想方法.

设计意图引导学生在新课结束后复盘反思,加深对新概念的整体认识,进一步深化对新概念所在的知识体系的理解和掌握.通过课堂小结,梳理学习的知识,提炼研究问题的方法,在引导学生加深对数列概念理解的同时,进而领会获得数学概念的基本方法,让学生不仅很好的“学会”,而且做到“会学”.

4 教学反思

作为大概念背景下的章节起始课,本节课在教学中以大量生活案例作为情境,让学生体验数列概念的背景,不断地类比函数的概念及研究过程.整节课是在学生与已有知识的不断对比中层层深化,整个教学过程一气呵成,自然流畅. 借助教师创设的教学情境场,结合学生已有的知识结构,抓住数学本质,将自身知识融会贯通、迁移应用,渗透知识的理解性学习和体系化构建,发展数学思维,最终提升数学综合素养,获得深度学习.

4.1 大概念教学更加注重概念产生的情境——大概念的“源”

新课标指出,学习是基于情境的.因此,创建有意义的“情境场”,可以建构学生已有的概念体系,有效链接学生内在的知识、技能和经验.而数学教学的情境创设,可以是生活中具体事例、文学史料,也可以基于学生已有的知识结构创设问题情境,用问题串联新旧知识.

本文研究的数列教材中是以剧场座位、彗星出现的年份、“一尺之棰”的剩余部分、各年枝干数、奥运金牌数等六个生活或史料中的案例作为情境引入数列概念,得到数列概念后又以堆放的钢管数和工资为例辨析概念.本案例中的情境基于函数大概念,从学生已有的知识机构探究,类比函数提出的新问题,使学生产生了认知冲突,从而激发学生对数列的继续研究.

基于大概念设计形成的情境,不拘泥于生活中的具体情景,可以从问题出发,结合具体的教学内容,再根据教学内容的大概念单元内的知识点以及各知识点之间的结构,从点到面,从特殊到一般,让学生的思维在认知冲突中走向升华,这也是大概念教学设计的核心.

4.2 大概念教学更加注重学生的知识结构 ——大概念的“质”

学生的知识结构指的是学生的最近发展区,即学生已有的知识结构和思维方式.新概念的学习是在学生已有的知识结构上,新旧知识相互渗透重组的过程,因此,基于大概念下的问题设计和探究都要从学生已有的认知水平和经验出发,引导学生经历观察和分析、猜测和验证,积极、主动地参与课堂教学,不断在活动中积累认知经验,从而在新的情境中进行知识迁移,理解并掌握新概念,提高思维层次,提升数学素养.

本课教学中,学生在学习数列前,已学习了函数及其研究方法的知识体系,因此,在设计数列的教学过程中,引导学生类比函数,基于函数这个大概念,从按照数列的现实背景——数列的概念(定义、表示)——数列的性质——特殊数列——数列应用等方面去研究数列.

总之,要给学生一碗水,教师必须要有一桶水.授课前,教师必须要熟知学生的认知、理解课堂生成、读懂学生“困惑”,才能更好地理解“学”与“教”的关系,这样的课堂才会碰撞出更多精彩的知识生成,使教学更有实效,学生真正做到想学、爱学.