立体几何教学中的降维与升维策略

西藏山南市第二高级中学 刘冬喜 周宗杰 (邮编:856000)

数学中,维是指一个问题中元素的自由度,即该元素的坐标数,如数轴上点的维数是1,平面内点和直线的维数是2,在空间中点和平面的维数是3等等.降维则是通过一些数学方法,将高维的数学问题降为低维的数学问题,从而使问题简化,达到解决问题的目的.

降维,作为一种数学方法,意指如:一般问题的特殊值解法,多元减为少元,立体几何问题转化为平面几何问题等等.降维方法是处理数学问题的一种行之有效的方法,但在教学中还不仅要介绍降维方法,更要进一步对知识与知识结构之间的关系进行更深的提炼、概括和总结,使学生获得更深入的认识,从而上升到意识领域,形成一种解题思想——降维思想,即将一个维度较高的数学问题转化为较低的数学问题,通过简化问题结果,缩小问题视角,减少变化因素,探求解决问题的方法的思想.这对培养学生的核心素养能起积极的作用.

立体几何中的四条判定定理从条件到结论体现了升维思想,而四条性质定理从条件到结论体现为降维思想.降维思想是立体几何的主体思想,通常通过射影法、平移法、旋转法、对称变换等方法将空间三维问题降为平面的二维问题.

例1空间中从同一点出发的三条射线,每两条所成角的平分线与第三条射线确定一平面,如此所得三个平面必相交于同一直线.

分析假如我们能作一个适当的平面分别交三条射线和三条角平分线于A、B、C、L、M、N,如图1,三平面OLC、OBN、OAM都过O,要证它们相交于一直线,只需找另一公共点,为此我们降一维联想到平面几何中三角形三条中线交于一点,这样只要在三射线上各取OA=OB=OC,则过A、B、C作平面ABC,L、M、N分别是AB、BC、AC的中点,便可证得所欲证的结论.

图1

证明作OA=OB=OC.因为OL,OM,ON分别是角平分线,所以L、M、N分别是AB、BC、AC的中点,所以三角形的三条中线AM、BN、CL交于一点G.则OG就是面OLC、面OBN、面OAM的交线.

平面几何研究的是平面图形及其数量关系,立体几何则是研究空间立体及其数量关系.由平面几何到立体几何是由二维空间进入到三维空间,它们之间有着紧密的联系,注意研究它们之间的联系,弄清它们之间的区别,在立体几何问题中注意降一维联想平面几何问题的解法,从平面几何问题中得到启发,再升一维探求立体几何问题的解法,常常使复杂的立体几何问题解题思路探求过程得到简化.因此,在教学过程中,加强平面几何和立体几何之间的横向联想,对培养学生的逻辑思维能力是有益处的;对拓展学生的知识境界,由二维到三维以至今后对n维空间的探索也是大有裨益的.

分析降一维联想平面几何问题(梅涅劳斯定理):空间四边形→三角形截面→截线.

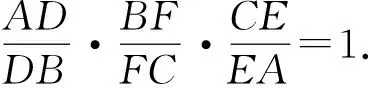
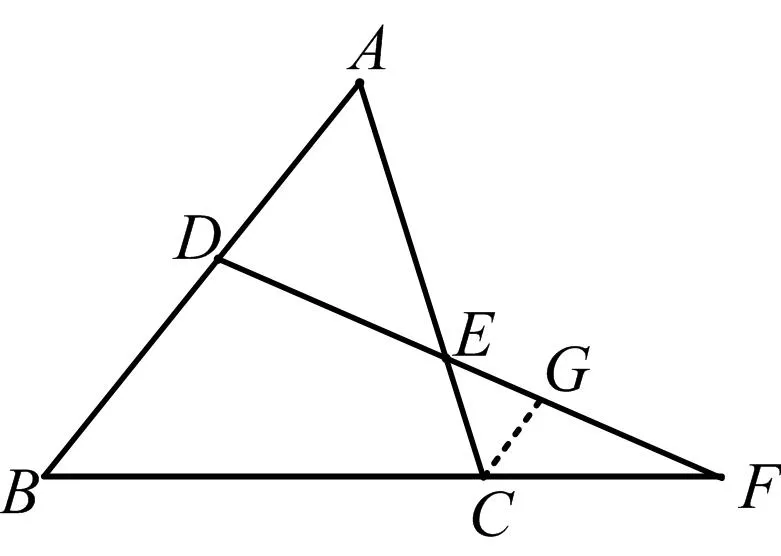
图2

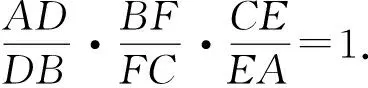
从上面的证明思路启发,平面中作平行线构造比例线段,空间里可以作平行平面构造比例线段.从而升维证明立体几何问题.

证明如图3,当平面α∥BC时,显然BC∥DE∥D′E′,

图3

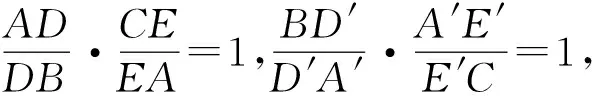
如图4,当平面α不平行BC时,不妨设点B到α的距离较近,则过点B作平面BFF′∥α,分别交AC、A′C于F、F′.

图4

所以,DE∥BF,D′E′∥BF′,FF′∥EE′,

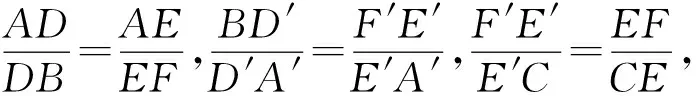
再如平面几何中证含有线段平方的等式时常用勾股定理和射影定理.在立体几何中类似问题则可以考虑在各种不同的直角三角形中构思相应的等式.

分析降维联想平面几何问题:三棱锥→三角形;锥高→形高.

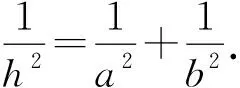
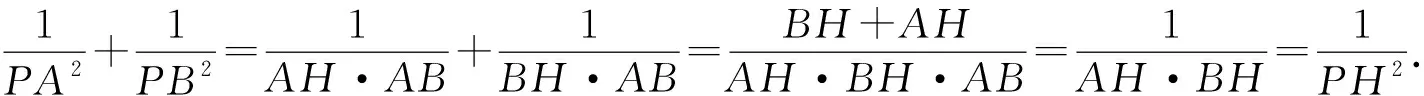
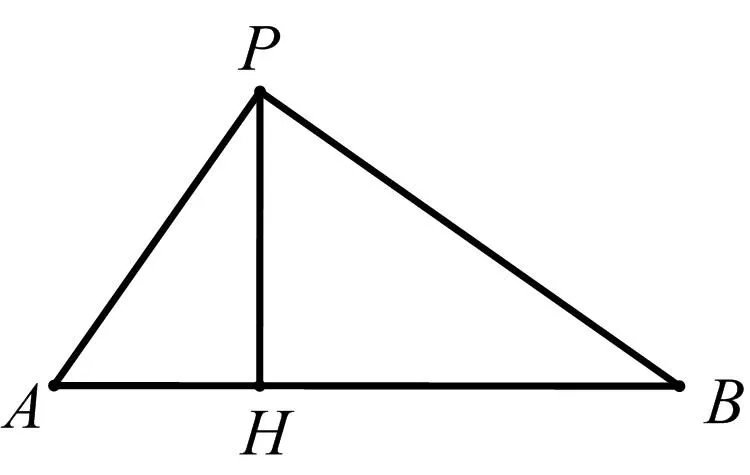
图5

由以上问题得到启发:在三棱锥P-ABC中,作Rt△PBC的弦高PD,则PH必为Rt△PAD的弦高,两次使用射影定理获解.

升维联想立体几何问题:

证明如图6,过P作PD⊥BC,垂足为D,易证PH⊥△ABC.

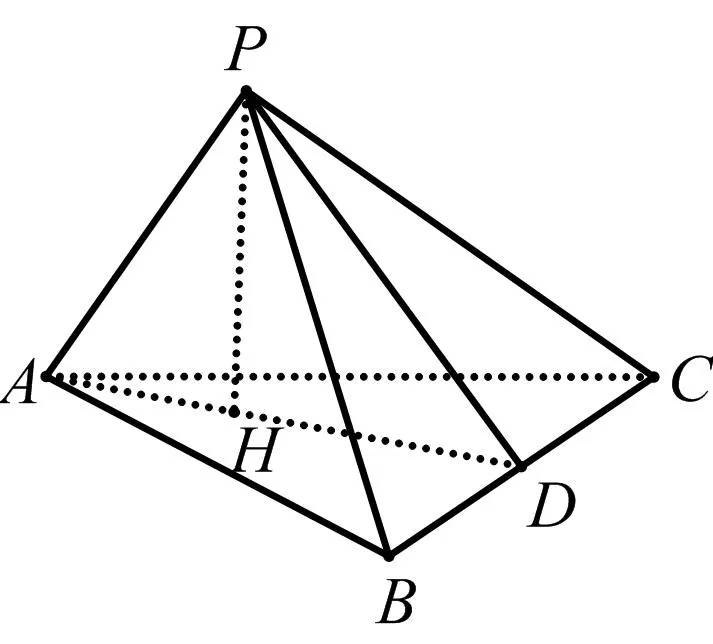
图6

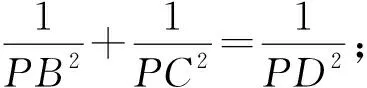
平面几何中,“等边三角形中任一点到三边的距离之和为定值”,立体几何中,“正四面体中任一点到四个面的距离之和为定值”.证法上,前者用面积,后者用体积,类似的问题亦可仿证,如例四.

例4已知在正四面体ABCD的底面BCD的外侧有一点P,点P到底面的距离是h,点P到三个侧面的距离分别h1,h2,h3为.求证:h1+h2+h3-h为定值.

降维联想平面几何问题:正四面体→正三角形;锥高→形高.

平面几何问题:在正三角形ABC的底边BC外侧有一点P,P到BC的距离为h,P到另两边的距离分别为h1+h2,求证:h1+h2-h为定值.

证明如图7,设△ABC的边长为a,高为H,连接PA、PB、PC.

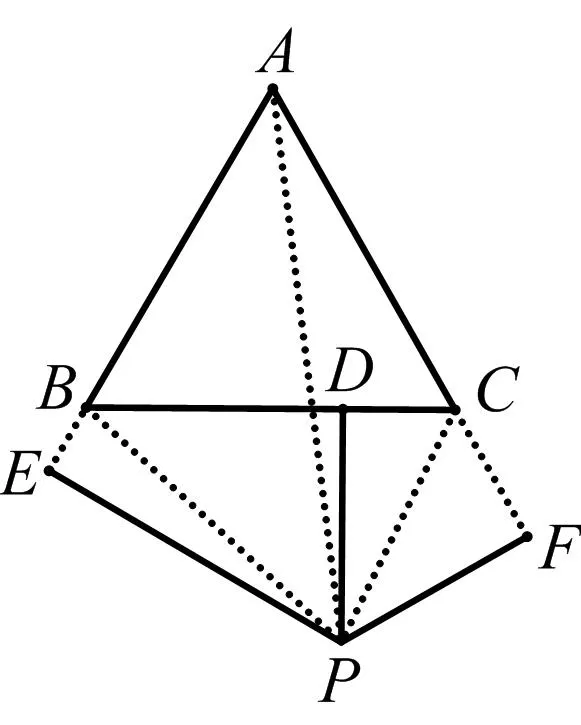
图7

所以S△PAB+S△PAC-S△PBC=S△ABC,

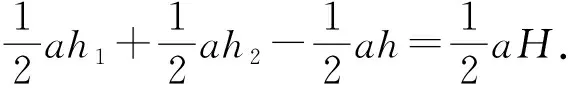
即h1+h2-h=H为定值.

由以上问题得到启发:有关距离(高)的问题,常常联系三角形面积,立体几何中联想到三棱锥的体积.

升维联想立体几何问题:

证明如图8,设正四面体每个面的面积为S,体高为H,连PA,PB,PC,PD.因为

图8

VP-ABC+VP-ACD+VP-ABD-VP-BCD=VA-BCD,

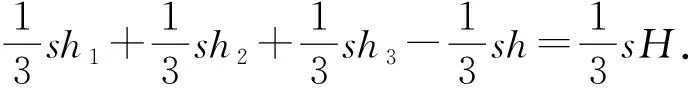
即h1+h2+h3-h=H为定值.

平面几何中,求三角形的面积用不同边作底可导出新的等式,立体几何中,用不同的面作底来求锥体体积也可导出新的等式,帮助解题,如例五.

例5已知长方体的三条棱AB=4,AA1=3,AD=6,求面对角线BB′与体对角线AC′的距离.

降维联想平面几何问题:长方体→长方形,异面直线间的距离→点到直线的距离.

平面几何问题已知矩形两邻边长分别是AB=3,AD=4,求点A到对角线BD的距离AE的长.

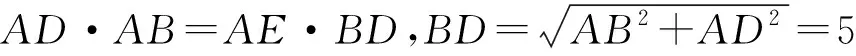
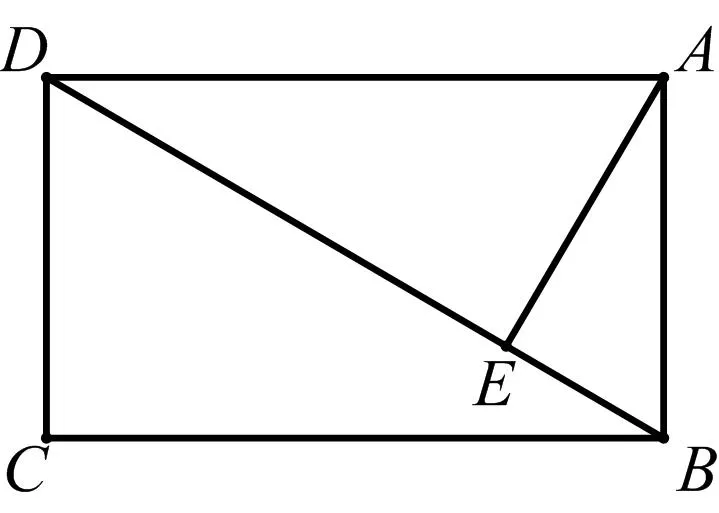
图9

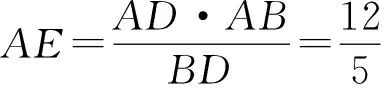
启发求三角形的面积可用不同的边作底边,求三棱锥的体积可以用不同的面作底面.

升维联想立体几何问题:

解如图10,将矩形AA′D′D向上延升一倍到NADM的位置,

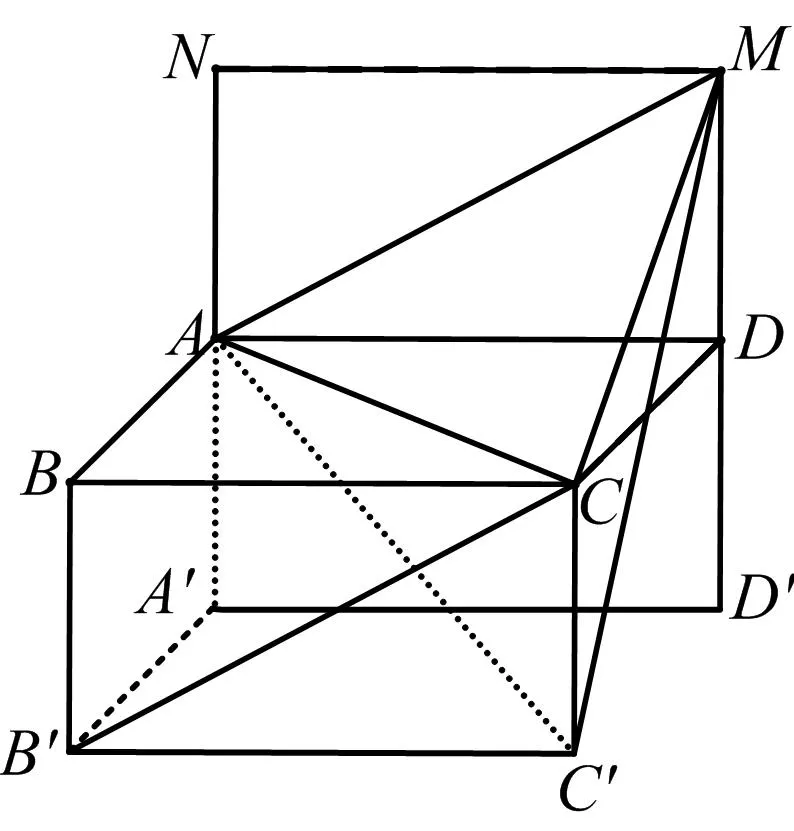
图10

因为B′C∥A′D∥AM,

所以B′C∥平面AC′M,

因此,C到平面AC′M的距离即BB′与AC′的距离.

所以,VM-ACC′=12.

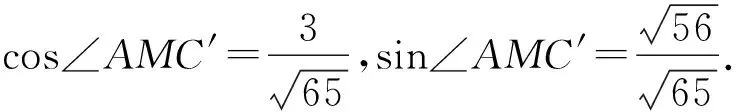
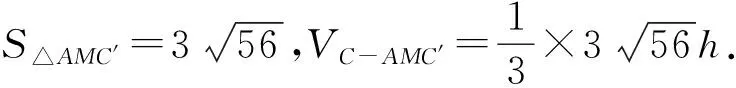
以上仅仅从几个侧面陈列了对立体几何题降维联想平面几何题,再升维寻找立体几何题解法的模式,其实,类似的问题还很多,诸如"对称问题在平面几何中的应用",是找关于直线的对称点来解题,在立体几何中则可找关于平面的对称点来解题;平面几何中关于圆的问题在立体几何中有不少题目可在球的问题中找到踪迹;平面几何的作图思路很多不乏为立体几何作图的先导,只要我们认真联想,反复对比,那么平面几何与立体几何的解题方法就可以相辅相成,相得益彰.