聚焦关键信息 联想基本图形 组织生成路径——2023年北京市中考数学第27题赏析

安徽省合肥市第四十八中学 陶兴高 丁永愿 (邮编:230002)

著名数学教育家波利亚说:“一个专心认真备课的教师能够拿出一个有意义的但不复杂的题目去帮助学生挖掘问题的各个方面,通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域[1].”解题是数学中必不可少的学习活动,具有巩固基础知识、培养思想方法、发展核心素养的功能．锻炼解题的能力固然要以做题为主,但不能仅仅停留在低层次的数学操作层面,教师在解题研究时,要关注解题思路的形成过程,积累数学活动经验．下面我们以北京市中考数学压轴题为例,阐述具体的探究过程．

1 原题呈现

(2023·北京)在△ABC中,∠B=∠C=α(0°<α<45°),AM⊥BC于点M,D是线段MC上的动点(不与点M,C重合),将线段DM绕点D顺时针旋转2α得到线段DE．

(1)如图1,当点E在线段AC上时,求证:D是MC的中点;

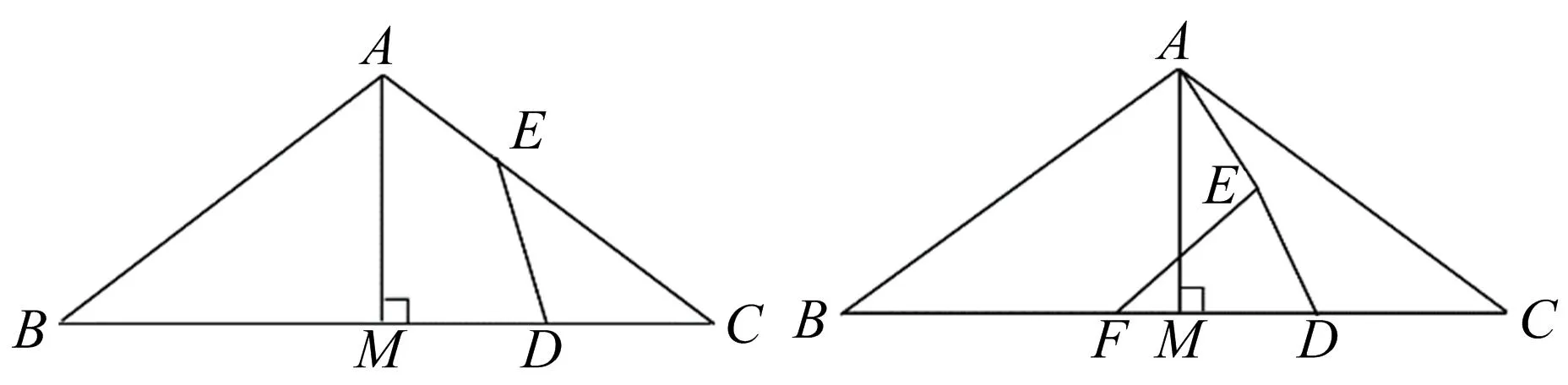
图1 图2

(2)如图2,若在线段BM上存在点F(不与点B,M重合)满足DF=DC,连接AE,EF,直接写出∠AEF的大小,并证明．

这是一道优秀的几何压轴题,题干简洁,问题明确,具有低起点、多视角、高目标的特点,以提高解决问题能力为目标,能够容纳不同思维习惯的学生,该问题内容简明,是以等腰三角形为背景的综合问题,考查了等腰三角形的图形与性质,旋转的性质,三角形的中位线、全等三角形的判定与性质等知识,兼顾考查了几何直观,演绎推理的能力,作出辅助线是解决该问题的关键．

2 试题分析

正确解答问题的基础是准确、全面地理解题目中所给的信息,如:题目中显现的条件是什么?隐含的条件是什么?与题目中信息相关联的知识有哪些?类似题目的解题经验有哪些?

第(1)较为简单,本文主要探究第(2)问,从条件出发:因为∠B=∠C=α(0°<α<45°),AM⊥BC于点M,可得M是BC的中点,又D是CF的中点,显然这是线段上的双中点结构,易得BF=2MD=2ED．该问题证明到此不能继续,需要构造辅助线,辅助线的构造需要根据问题中的关键信息进行联想,条件中的关键信息有中点,2倍角．中点的联想有倍长中线、中位线、斜边中线、三线合一等;2倍角的联想有等腰三角形、角平分线等．从结论出发:由图形可猜测∠AEF=90°,证明垂直的思路有三线合一、斜边中线逆定理、直径所对圆周角、相似(全等)三角形对应角相等、勾股定理的逆定理、反8字型导角(如图3)等．将条件的联想与证明垂直的思路结合构图,可形成不同的解题思路．

图3

3 解法赏析

思路一构造中位线

法1如图4,延长FE到H使FE=EH,连接CH、AH、AF．

因为DE是△FCH的中位线,则DE∥CH,CH=2DE,所以∠FDE=∠FCH=2α,得∠B=∠ACH=∠ACB=α,BF=CH,得△ABF≌△ACH(SAS),AF=AH,由等腰三角形三线合一得AE⊥FH．

法2如图5,连接AF,取AF中点I,连接ID、IE、IM.

图5

因为DI是△FCA的中位线,所以ID∥AC,∠IDM=∠C=∠EDI=α,易证△MDI≌△EDI(SAS),所以IM=IE,又在Rt△AMF中IM=IF=IA,所以IE=IF=IA=IM,所以A、E、M、F四点共圆,由直径所对得圆周角为直径得∠AEF=90°.

思路二倍长中线

法4如图6,延长ED至点G,使得ED=GD,连接ME、CG、MG.

图6

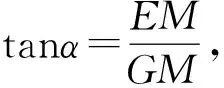
思路三构造角平分线

图7

思路四构造等腰三角形

法6如图8,过E作AC的平行线交BC于点G,连接ME．

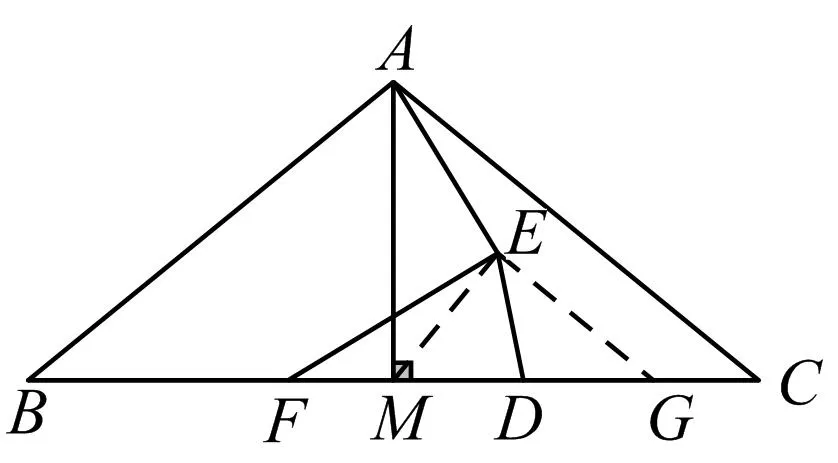
图8

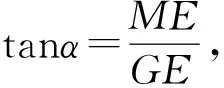
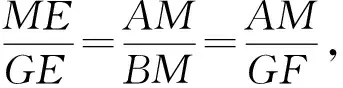
法7如图9,过D作BC的垂线交AC于点G,连接FG、FA．

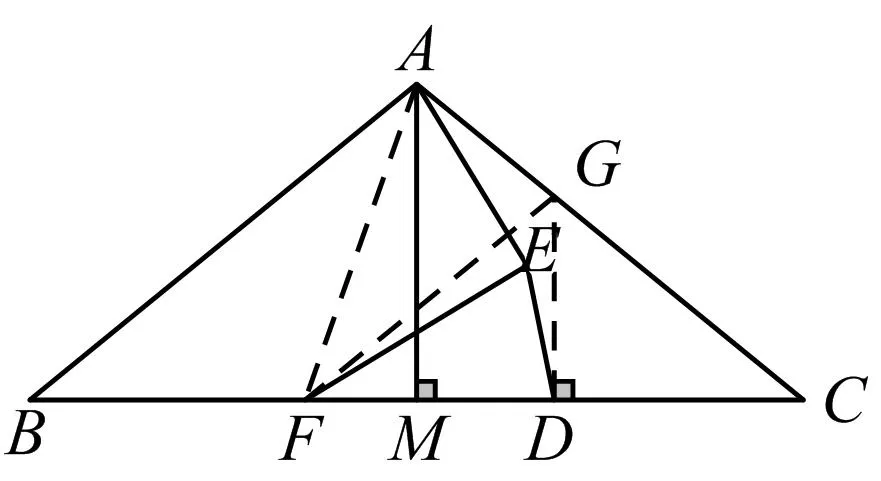
图9

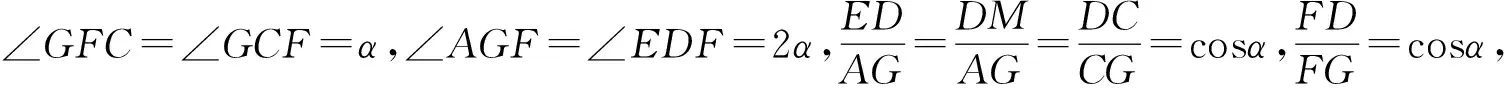
所以△EFD∽△AFG,由“手拉手”相似三角形一拖二的性质得△AFE∽△GFD,所以∠AEF=∠GDF=90°．

思路五创新思路

法8如图10,延长DE交AC于点G,过E作BC的平行线交AC于点H,连接EM.

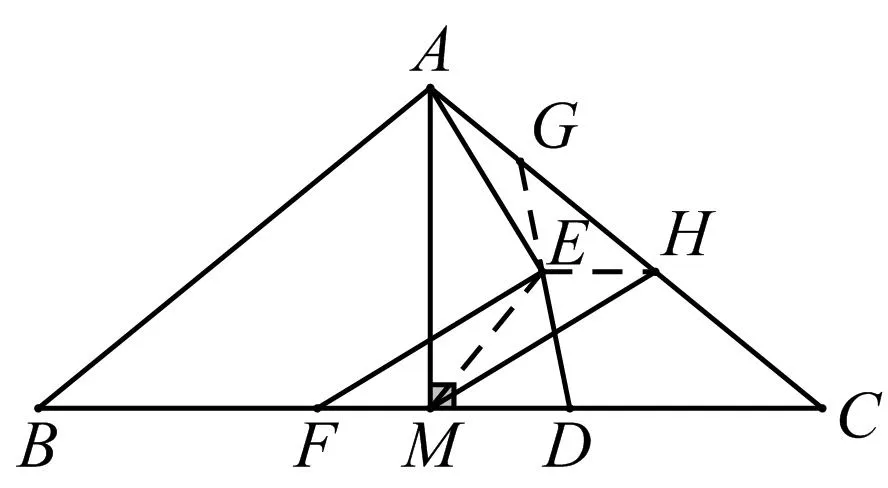
图10

因为ME⊥AH,EH⊥AM,所以点E是△AMH的垂心,所以AE⊥MH.又CD=DG,EH=EG,所以FM=FD-MD=DG-DE=EG=EH,所以四边形FMEH是平行四边形,故EF∥MH,AE⊥FE．该法十分简洁,主要运用等腰三角形和平行四边形解决,脱离了繁琐的相似(全等)三角形证明．此外,还可以解析法和向量法进行解决,不过这两种方法涉及到高中知识,明显超纲,可供学有余力的学生自行研究．

4 问题变式

在问题解决之后,如果能及时地引导学生对结论进行深层次的探究概括、变式拓展,可以培养学生主动探索知识的欲望,提高学生提出问题,分析问题的能力．

变式思路一由静到动

将问题(2)的条件“若在线段BM上存在点F满足DF=DC”改为“若在直线BM上存在点F满足DF=DC”,其余条件不变,结论是否依然成立?

变式思路二由正到反

增加第(3)问:如图2,点F在线段BM上(不与点B,M重合),连接AE,EF,若AE⊥EF,求证D是CF的中点．

5 解题反思

解题反思是解题活动的延续,是学会怎样解题、积累解题经验和培养思维深刻性与批判性的良好途径．通过对解题活动、特别是已有的成功实践的深入分析、总结反思,对今后的解题可起到一定的启发和指导作用．

5.1 积累基本图形,奠定构图基础

基本图形没有明确的概念,可以看成是解决问题中常用到的图形结构,为提高问题解决的效率,在日常教学中对于基本图形要有意识地积累和理解．一方面由于基本图形是常规图形的延申,如倍长中线模型来源于平行四边形,2倍角模型来源于等腰三角形和角平分线,因此基本图形的产生不应该是机械的记忆,而是要在探究常规图形性质时,有意识地进行图形变化,性质拓展,让学生体会基本图形的生成过程;另一方面应将基本图形赋予不同的几何背景,培养学生对基本图形的提炼和应用的能力,让学生体会基本图形的应用价值、应用条件及应用方法,增强学生的模型意识和几何直观．

5.2 注重一题多解,完善认知结构

在《义务教育数学课程标准(2022年版)》中指出[2],通过合适的主题整合教学内容,帮助学生学会用整体的、联系的、发展的眼光看问题,形成科学的思维习惯,发展核心素养．但该问题的参考答案仅仅用八年级数学知识进行解决,并未完全体现该问题蕴藏的知识方法,略显曲高和寡,多数情况下不同的几何构型可以找到不同的解题思路,以达到更广更全的知识复习及方法训练．在该问题中,题干可以挖掘出不同的关键信息;同一关键信息有不同的联想,如由中点可以联想中位线、倍长中线、斜边中线等;同一联想有不同的作图视角,如法1和法2同为构造中位线,但有着有不同的构图作法;同样的构图有着不同的证明思路,如法2用全等而法3用相似,殊途同归.从找关键信息,到联想构图,再到明确思路,每个环节都可以尝试发散,充分地揭示题目中的信息,丰富完善学生的认知结构,增强学生对新问题敢于联想分析,敢于创新,从而提高学生解决问题的能力．

5.3 渗透思想方法,提高核心素养

解题研究是让学生形成自己的数学思想和方法,学会用数学得眼光看待事物,学会用数学的思维解决问题[3]．在探究该问题时,由条件信息联想构图,体现了数形结合的思想;在问题分析的过程中,体现综合分析的方法;从图1到图2再到变式图,其实就是点F位置不断变化的过程,若将第(1)问改为连接EM写出∠AEF的大小,则整个题目的探究会显得更加流畅,这一过程渗透了特殊到一般的数学思想．在研究问题的过程中要注重积累解题经验,总结解题规律,感悟数学思想,帮助学生从知识学习走向思维学习．