基于层次分析法的学生组织满意度评价指标体系构建及实证研究

吕 琳，张晓玲

（1.复旦大学附属金山医院，上海 201508；2.上海市公共卫生临床中心，上海 201508）

高等学校学生组织是高校组织管理和人才培养的重要载体之一。目前，我国高校学生组织大致包括以下几种主要形式：班级组织、共青团组织、学生会组织、社团组织及其他的非正式组织[1]。学生组织是校园文化建设的重要推动者，其建设和优化不仅有利于学生自我管理、自我教育，还能提高学生的组织能力和整体素质，实现学生的全面发展[2-4]。当前，多数高校学生组织在运行过程中存在一些问题，具体表现为学生组织的思想引领力、覆盖力不足；学生组织的凝聚力、号召力弱，缺乏模范带头作用；学生组织的自主运营能力、自我革新能力不足；学生组织为学生服务的质量不高等[5]。产生上述问题的原因之一为，高校或院系未能形成针对学生组织认可度较高的完善的评价指标体系，导致学生组织成员之间交流协作效率低下，其内部成员的工作满意度不高，最终影响了学生管理工作成效。层次分析法（Analytic Hierarchy Process，AHP），是将复杂问题逐步分解成若干梯阶层次，使其简单化、层次化、系统化[6-7]。该方法通过定性与定量相结合处理各种决策因素，将人的主观判断用数量形式表达和处理，从而确定评价指标权重，并进一步构建出判断矩阵[6-8]。近年来其在社会经济研究的多个领域应用广泛，也被应用到满意度研究。本研究基于AHP 构建了针对学生组织满意度的评价指标体系。基于院系角度，通过评价指标体系的实证结果分析，可以探究影响学生组织满意度的薄弱环节，制订相应改进举措后进行重点突破，从而形成学生组织建设优化的良性循环。基于学生角度，评价指标体系的反馈结果可为学生管理工作发挥激励和正面导向作用。

1 资料来源与方法

1.1 调查对象

以上海市某高校两家三级附属医院的在读研究生为调查对象，采用线上问卷调查的方式对3 个不同学生组织进行满意度测评。

1.2 研究方法

首先，运用层次分析法进行模糊量化分析，确定学生组织满意度评价指标体系模型的目标层、一级指标和二级指标。其次，运用专家评分法对不同层次的各项指标进行重要性判断，并对指标权重进行科学赋权。最后，根据构建好的评价指标体系制作调查问卷，在上述调查对象中进行测评。

1.3 统计学分析

采用Excel 整理数据，采用Graphpad Prism 进行统计分析。运用方差分析检验不同学生组织满意度在各指标分值和满意度综合评价值上的差异。

2 结果

2.1 构建评价指标体系模型

对学生组织满意度影响因素进行多维度分析，运用AHP进行模糊量化分析，将评价指标体系确定为目标层A、包含4个指标的一级指标层B 和包含12 个指标的二级指标层C （见表1）。

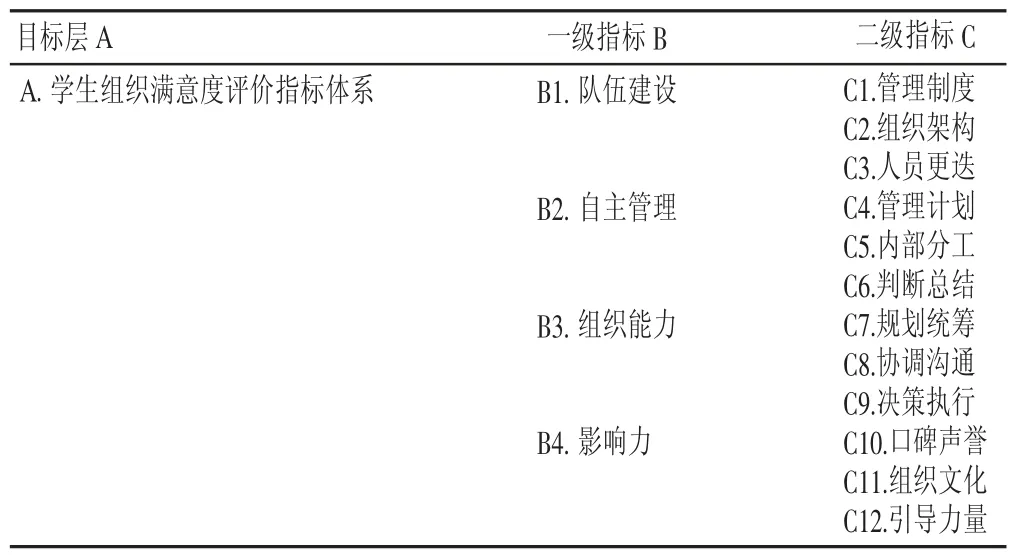
表1 学生组织满意度评价指标体系Table 1 Evaluation index system for student organization satisfaction

2.2 评价指标重要性判断和权重确定

根据指标评分说明（见表2）对各指标进行重要性判断。采用专家评分法，依据指标间的重要性进行两两对比，得出一级指标评分值（见表3）。其次，采用算术平均法，得出一级指标层判断矩阵（见表4）。进一步采用上述方法，计算二级指标的评分值和二级指标层判断矩阵。

表2 指标评分说明Table 2 Indicator scoring explanation

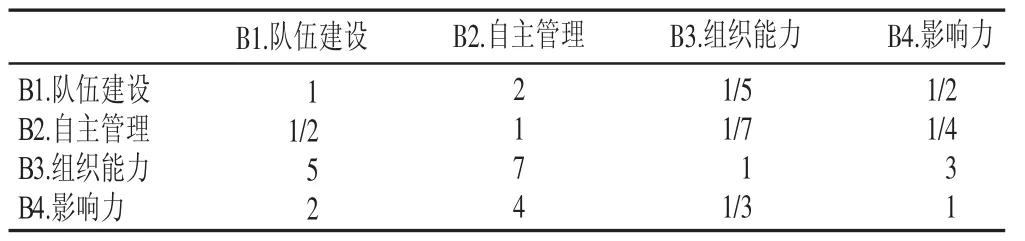
表3 一级指标层各指标的重要性Table 3 Importance of each indicator in the first level indicator layer

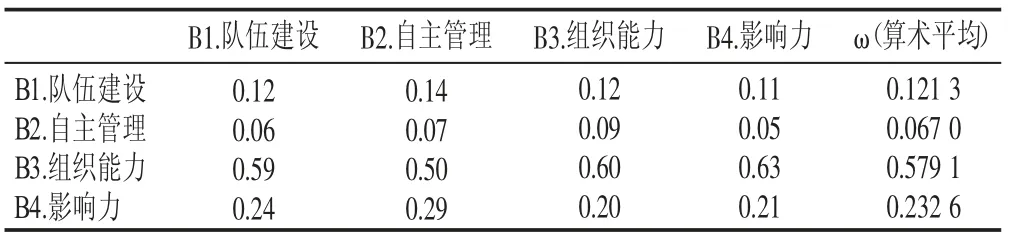
表4 一级指标层判断矩阵Table 4 First level indicator layer judgment matrix

2.3 一致性检验

为检验一级指标层判断矩阵的一致性，计算一级指标层判断矩阵的各指标权重特征向量Wi 和特征向量的最大值λmax。经过归一化处理得到特征向量W=（ω1，ω2，ω3，…，ωn）和一致性指标CI 值。存在判断值CR = CI/RI，当CR＜0.1 时，认为判断矩阵的一致性程度可被接受。平均随机一致性指标RI 由判断矩阵阶数所决定，不同阶数对应的RI 值见表5。由于一级指标层判断矩阵的阶数为4，RI 值取0.89。经过计算，特征向量的最大值λmax=1.001 771，CI =（λ-n）/（n-1）=-0.999 409 646，CR =-1.123＜0.01，因此上述一级指标层判断矩阵均符合一致性检验。

表5 平均随机一致性指标RI 值Table 5 Average random consistency index RI values

同理，采用上述方法，计算二级指标层判断矩阵的各指标权重特征向量Wi 和特征向量的最大值λmax，检验二级指标B1～B4 各层判断矩阵的一致性。B1 到B4 的λmax分别为：1.008 858 259、1.002 863 486、1.001 085 7 和1.000 863 867，CR 均＜0.01，因此上述二级指标层判断矩阵均符合一致性检验。根据上述研究结果，可确定学生组织满意度评价指标体系一级、二级指标的权重，对二级指标的评价内容进一步细化，从而建立学生组织满意度评价指标体系模型（见表6）。

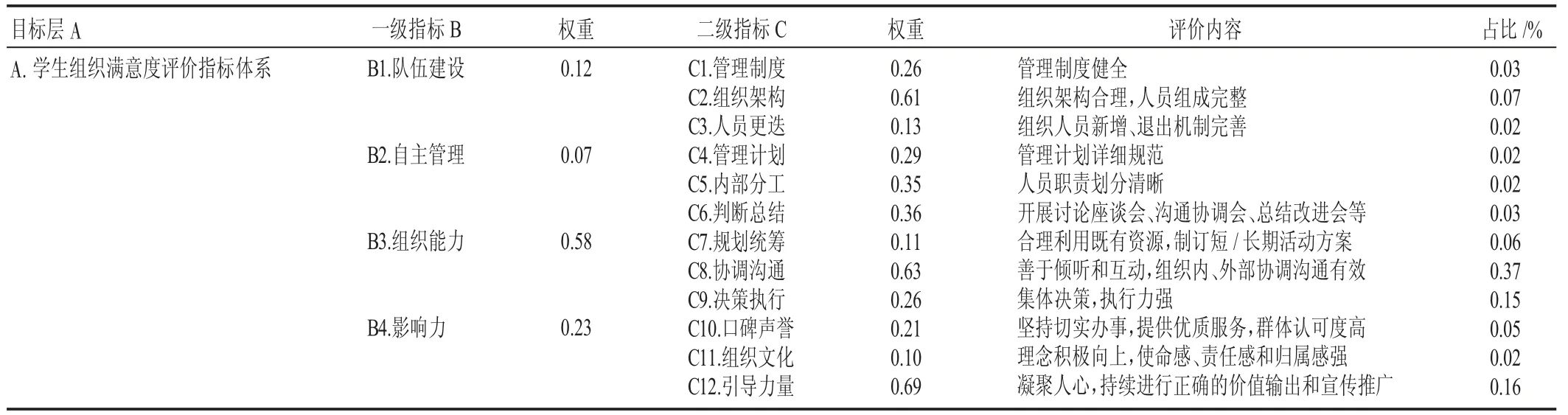
表6 学生组织满意度评价指标体系模型Table 6 Model of student organization satisfaction evaluation index system

2.4 评价指标体系的实证

采用案例验证，对所构建的评价指标体系的可操作性进行验证。2023 年4 月，选择上海某高校的两家三级附属医院，对其医学研究生发放问卷，分别对两家医院的学生党支部、学生团支部和研究生会进行满意度测评。回收问卷，对整理后的数据进行算术平均处理，得出每个指标的分值。计算公式为：N=N1+N2+N3+N4。N1～N4 为4 个一级指标分值，N 为学生组织满意度综合评价值。N1～N4 的计算公式为：Ni=Wi∑WijNij，其中Wi为W1～W4 4 个一级指标的权重，Wij为一级指标下对应的二级指标的权重，Nij为一级指标下对应的二级指标的得分。本研究共回收问卷70 份，其中参与学生党支部满意度调查24 人，参与学生团支部满意度调查20 人，参与研究生会满意度调查26人，问卷有效率100%。统计结果显示，某三级乙等医院的学生党支部满意度最高，综合评价值高达97.56，且各指标分值波动小。某三级甲等医院的学生团支部、研究生会的综合评价值分别为91.55 和87.59，在B3 指标的调查分值上波动较大（标准差分别为6.18 和6.80）。此外，不同学生组织在各指标分值和满意度的综合评价值上差异具有统计学意义（P<0.05），见表7。

3 讨论

3.1 组织能力是影响学生组织满意度的主要因素

在本研究构建的学生组织满意度评价指标体系模型中，B3组织能力的权重为0.58，在4 个一级指标中占比最高，其中C8协调沟通最突出。该重要性判断的结果提示：组织能力是影响学生组织满意度的主要因素，而沟通协调是其重要组成部分。以往研究表明：组织领导力是组织能力的主要体现，强有力的组织领导能够在内部整合、资源协调、执行管理、政策影响力、利益相关者关系的协调等方面发挥积极影响[9]。学生骨干是学生组织活动的主体，学生组织应充分发挥学生骨干的模范带头作用。著名管理学家巴纳德认为，沟通是一个组织的成员联系在一起，以实现共同目标的手段。也有学者认为，沟通是人们通过语言和非语言方式进行的双向互动过程，在彼此了解与理解的基础上，相互融合、认同，进而共赴愿景。协调是管理者为确保组织目标的实现，运用各种方法，协商、调整组织系统内部各部门之间、人员之间、组织系统与其外部环境之间的关系，使之分工协作、互相配合、和谐有序地完成组织目标的行为[10]。由此可见，可通过共同制订组织目标，提高学生参与度，促进团结协作，达成共识，提高学生组织工作开展效率[11]。

3.2 不同学生组织的满意度测评结果存在差异

满意度评价的实证结果表明：某三级乙等医院的学生党支部综合评价值最高，且各指标分值的标准差较小，提示调查对象对学生党支部的满意度高且较一致，该组织能较好地满足学生群体的服务需求。某三级甲等医院的学生团支部、研究生会的综合评价值相对偏低，尤其在B3 指标的调查分值上波动较大，提示组织能力是影响该两个组织满意度的薄弱环节。此外，不同学生组织在各指标分值和满意度的综合评价值上差异具有统计学意义（P<0.05），表明学生党支部在各方面的表现优于学生团组织和研究生会，可将其作为借鉴对象，对另外两个学生组织进行优化。

4 结语

本文从学生组织满意度的角度出发，运用AHP 构建了学生组织满意度评价指标体系模型，并对上海某高校两家三级附属医院的3 个学生组织进行了调查，获得了实证研究结果，证明该评价指标体系真实有效。对于任一给定的学生组织，均可以通过该评价指标体系调查一定数量的样本，计算出满意度的各级指标分值和综合评价值，从而针对性地持续改善与提升影响满意度的薄弱环节，因此，本研究结果对学生组织的建设优化能起到较好的指导作用。