基于深度神经网络的含运动边界非定常流场预测方法研究

韩仁坤，杜焦喜，刘子扬，李立，陈刚

1.西安交通大学 机械结构强度与振动国家重点实验室，陕西 西安 710049

2.西安交通大学 先进飞行器服役环境与控制陕西省重点实验室，陕西 西安 710049

3.航空工业计算技术研究所，陕西 西安 710049

飞行器气动弹性问题是研究飞行器结构与气动力相互耦合关系，是一种典型的流固耦合问题。工程实践中常使用计算流体力学（CFD）和计算结构动力学（CSD）耦合的策略模拟获得飞行器气动弹性响应过程。但是CFD/CSD 耦合计算耗时严重，特别是在需要反复迭代修改的飞行器初步设计阶段，模拟耗时是让人难以接受的。气弹问题模拟中主要耗时过程是CFD求解流场演化的过程，因此许多研究者尝试使用数据驱动的方法模拟流场系统，实现流场的快速预测[1]，从而减少整个耦合过程的模拟耗时，如模态法、系统辨识法等。目前，针对非线性较强的流固耦合问题，仍缺乏结构运动影响下的高精度流场快速预测模型。

近年来，迅速发展的深度神经网络技术依赖于其强大的非线性学习能力，以及深度特征捕捉能力，在流场建模问题中已经取得了诸多成功应用[2-4]。深度神经网络在流体力学中的应用主要可分为三种方式：第一种是学习流体力学控制方程中某些参数变化规律，基于高精度数据校正控制方程，以提高方程在其他问题求解中的精度，如湍流模型中雷诺应力项的学习[5-6]；第二种是学习流动工况与流场之间的演化关系，给定流动工况神经网络即可预测出此刻流场状态，快速实现流场高精度重构[7-8]；第三种是学习流动工况与宏观气动力之间的映射关系，已知流动工况和几何外形可快速预测流场中结构受力情况[9-10]。

流场重构类方法因能快速给出当前流场状态而备受关注。基于深度神经网络的定常流场重构[7]通过构建翼型几何形状和流动工况至空间点处的流场信息之间的映射模型，实现了对不同翼型绕流场的快速预测。非定常流场时空演化特征建模，主要是通过流场降阶结合深度神经网络预测低维时间演化过程实现，降阶方式包括本征正交分解（POD）降阶[11]和神经网络降阶[12]。通过求解流场在低维空间上的时空演化过程，可极大缩短非定常流场时间推进模拟的耗时。

现阶段，使用深度神经网络对非定常流场进行建模研究，主要集中在固定边界绕流问题上。对于含运动边界非定常流场的建模，流场演化不仅受流场自身特性影响，还受结构运动的影响，这增大了建模难度。多采用响应预测类方法，直接预测运动边界的受力情况[13]。但此方法无法获得系统内部状态演化情况，不能应用于流动控制。Han Renkun等[14]通过对长短时记忆（LSTM）神经单元内部结构的修改成功将运动边界位置信息引入神经网络中，实现了含运动边界的非定常流场深度学习建模。本文以此为基础，进一步改进边界运动信息引入方式，优化数据结构，从而提高模型预测精度，获得流场中运动物体更准确的受力情况。

1 方法

1.1 神经网络结构

含运动边界的非定常流场建模的关键是如何将边界运动信息引入神经网络中，使其能够同时学习到前一时刻流场的影响和边界运动的影响。本文仍采用卷积和LSTM相结合的方式构建非定常流场预测模型，如图1 所示。整个预测模型中卷积层是为了捕捉流场深层结构特征，并降低流场维度，LSTM 层则用于根据前一时刻流场特征预测下一时刻流场特征。

图1 神经网络框架Fig.1 Neural network framework

图2 中展示的是长短时记忆神经网络中一个神经元的结构，每个神经元都包含三个门控机制（遗忘门、记忆门和输出门），使数据有选择地输出，从而避免了梯度消失。（1）遗忘门ft：对上一个节点传进来的输入进行选择性忘记；（2）记忆门it：对上一个节点传进来的输入进行选择性添加至单元状态ct；（3）输出门ot：结合当前神经元状态决定上一个节点传进来的输入中哪些将会被当成当前神经元的输出。每层长短时记忆神经网络由一个或多个神经元组成，前一个神经元输出的神经元状态ct-1和隐藏状态ht-1将作为下一个神经元的输入，以实现时间维度上的连续预测。

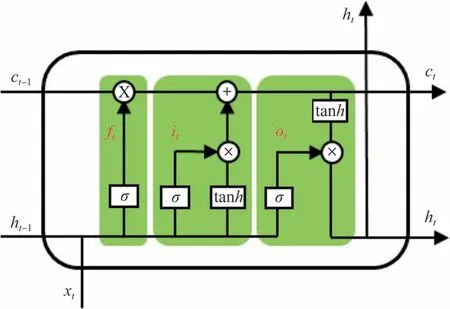
图2 长短时记忆神经网络神经元Fig.2 Long short term memory neuron

本文建模的目的是基于前一个时刻的流场和结构运动信息预测下一时刻的流场状态。因此，将前一个时刻的流场状态作为LSTM层神经元的时间序列输入xt，预测时刻的流场状态作为LSTM 层的输出。为将结构运动引入神经网络中，本文使用结构运动速度作为LSTM层第一个神经元的单元状态c0，结构运动幅值作为第一个神经元的隐藏状态h0。这样保证了下一时刻的流场是在上一时刻流场信息和结构运动信息共同作用下的预测结果，使神经网络能够学习到两种数据对流场演化的影响。整个神经网络层布置及卷积核等超参数的设置见表1。输出尺寸中第一位为批次大小，中间两位为二维特征图像尺寸，最后一位为特征通道数。

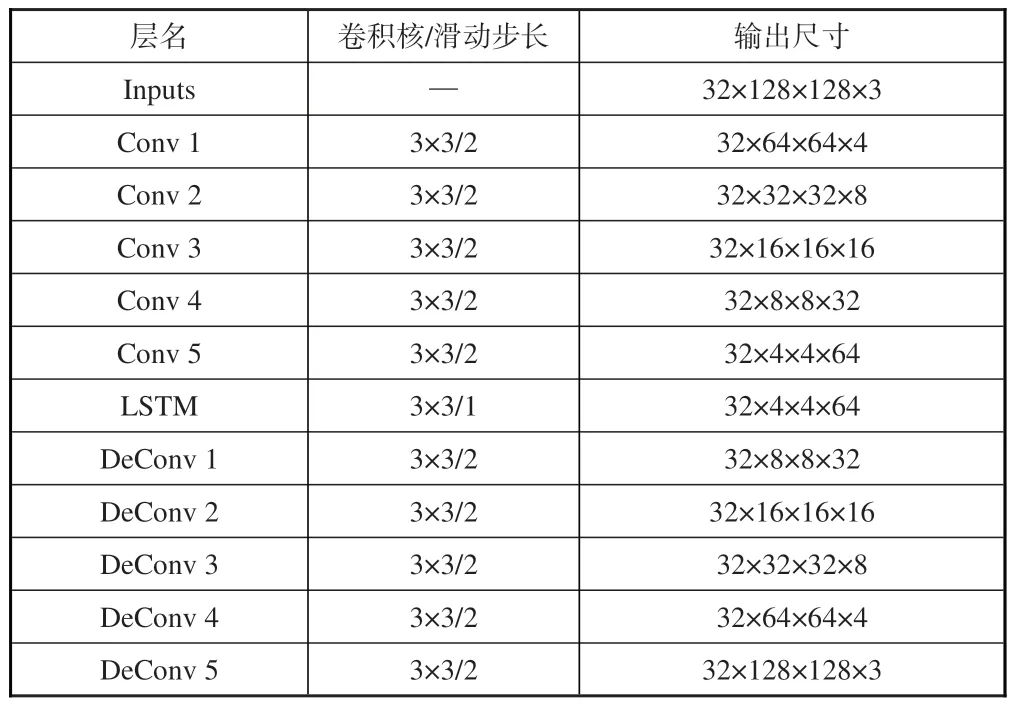
表1 神经网络结构参数Table 1 Neural network structural parameters

1.2 数据准备

本文拟采用神经网络对二维强迫振动下圆柱周围非定常流场演化过程进行建模。通过求解如式（1）所示的无量纲化的二维不可压流体控制方程，得到流场演化过程所有时刻的空间场数据。基于组内开发程序，采用有限体积方法求解方程，空间离散格式为二阶Van Leer格式，时间推进方式为LU-SGS隐式方法。流场区域及圆柱振动形式如图3 所示。圆柱直径为1D，圆柱距入口及上下边界距离均为15D、距出口为30D。圆柱采用单自由度正弦振动，改变振幅和频率获得多组工况下的流动数据

图3 流场求解域示意图Fig.3 Schematic diagram of flow solution domain

流场求解采用结构化网格，并且在结构边界周围采用O 形网格，如图4 所示。分别使用了网格量为12752 个、23544个和45944个的三套网格进行测试，结果表明中型网格量求解升阻力与最密网格求解结果误差在1%以内，达到收敛状态，并在此网格上对比了时间步长的影响，时间步长设置为0.001 可兼顾精度和效率。升阻力系数与试验结果的误差在4%以内，验证了仿真结果的可靠性。

图4 流场求解结构化网格Fig.4 Structured mesh for flow field simulation

基于结构化网格求解得到的流场数据为点数据格式，本文所采用的卷积神经网络所需要的数据格式为类似图像的二维像素数据，因此需要对模拟数据进行预处理，得到适应于神经网络的数据结构。本文采用将物面附近O形结构化网格沿径向展开的预处理方式，将O 形分布数据展开至正交分布的数据，保留了原始CFD数据点之间的相对位置关系，避免了Han Renkun等[14]在工作中使用投影法将CFD数据投影至均匀分布的笛卡儿网格点上而导致的弯曲物面表达能力不足、物面预测结果出现锯齿现象。

1.3 神经网络的训练

神经网络的训练过程是一个参数寻优的过程，将损失函数作为优化目标，通过数据前向传播和误差反向传播不断优化神经网络中的权重参数，以达到最优的预测效果。本文使用华为公司推出的新一代深度学习框架MindSpore构建神经网络模型，并利用其自动微分算法训练神经网络。损失函数采用的是如式（2）所示的均方根误差RMSE，采用Adam算法根据预测损失值逐步优化模型。

其中，ψt i和ψto,i分别为第i个数据点的预测值和真实值；N为数据点个数。

2 结果及讨论

本文以二维均匀来流中正弦强迫振动圆柱非定常流场绕流为例，展示本文所提出的神经网络框架对含运动边界非定常流场演化的学习能力及预测精度。通过改变圆柱振动形式获得不同工况下的流场数据供神经网络学习，振动频率与圆柱不动时流场频率一致，在振动幅值维度选择振幅比为0.25、0.30、0.35、0.40和0.45，一共获得5组不同工况下的流场数据。以前4 组数据作为训练数据集；以外插工况振幅比为0.45 时的数据作为测试集，以检测训练完成的神经网络模型的预测精度及泛化能力。振幅比为0.45时的升力系数与振幅比为0.4 时差距超过5%，且与训练数据中的升力系数区间的距离超过区间大小的40%，因此使用此状态的预测结果足以展示神经网络模型的泛化能力。

图5 所示为基于4 组训练数据训练完成的神经网络在振幅比为0.45 的工况下的流场单步预测结果，预测流场均方根误差RMSE值小于0.01。流场中误差较大的区域主要存在于尾缘距物面较远位置，而在物面附近区域预测精度较高。这是由于较远区域内流场变化较为平缓，物面附近区域流场变化较为剧烈，因此物面附近预测结果是决定损失函数值大小的主要因素，网络参数主要用于提高对物面附近区域的预测精度，而对远场区域变化不敏感。而物面附近区域流场状态是工程设计中最关心的，因此本文所采用的方法具有一定的优势。图6中展示的是此刻表面压力预测值与真实值的对比，可以看出，预测值光顺且较为准确，这进一步验证了流场的预测精度。

图5 单步流场预测结果Fig.5 Single step flow field prediction results

图6 单步预测圆柱表面压力结果Fig.6 Surface pressure of single step prediction

在非定常流场持续预测过程中，采用循环预测的策略，将当前时刻流场预测结果作为下一时刻预测的输入数据。图7展示的是神经网络模型在仅给定初始流场条件及结构强迫振动形式的情况下，预测的一个振动周期内流场演化过程。预测流场分布形态符合物理规律，且光滑无锯齿。图8展示了多个周期内预测流场与真实流场之间的RMSE误差，误差值均小于0.02，且没有持续增长的现象。这证明神经网络模型掌握了非定常流场演化规律，对局部预测误差不敏感，预测过程中误差累计现象不明显。

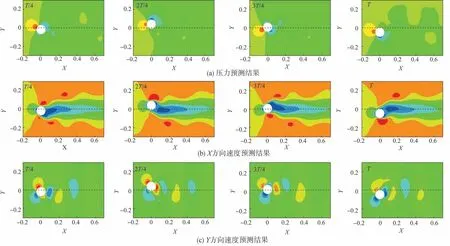
图7 一个振动周期内流场预测结果Fig.7 Prediction results of flow field within a vibration cycle

图8 整个振动过程中预测流场的RMSE误差Fig.8 RMSE error prediction results during the vibration process

通过积分每一时间步预测流场中物面压力可获得结构所受的升阻力。从图9中可以看出，预测结果与真实值幅值和频率均吻合较好，证明了本文提出的边界运动信息引入方式是有效的。且升阻力积分结果没有出现文献[14]中提到的不规则锯齿现象，证明了基于网格展开的数据结构比投影法具有更准确的物面压力分布表达能力。

图9 整个振动过程中圆柱所受升力预测结果Fig.9 Prediction results of the lift force on the cylinder during the vibration process

3 结束语

本文改进了一种基于神经网络模型的含运动边界的非定常流场预测模型，通过优化运动边界引入形式和实用新型数据结构，模型预测精度和泛化性能得到了进一步提升。以单自由度正弦振动圆柱绕流为例，神经网络模型学习不同振动频率和振幅下的非定常流场演化过程，可在学习参数范围外完成对非定常流场演化过程的预测，结果表明神经网络模型具有较高的预测精度和较好的泛化性能。

下一阶段将围绕飞行器气弹设计进一步开展研究，探索二维翼型和三维机翼的流固耦合建模方法。如要实现流固耦合响应的准确预测，还需进一步提高流场预测精度，尤其是物面表面压力。另外，更有效的运动边界引入形式决定着流固耦合模型的参数泛化能力。因此，仍需要从精度和泛化性两个方面改进和完善神经网络模型。