航空发动机燃油管路概率疲劳极限测试方法

刘伟，韩天宇，吕朋蓁，郭闯

1.西北工业大学，陕西 西安 710129

2.中国航发四川燃气涡轮研究院，四川 成都 610599

航空发动机燃油管路系统是燃油输送的通道，由于长时间处于内压和外部振动的工作环境中，管路结构易发生不同程度的疲劳损坏，成为航空发动机的主要故障源。疲劳极限是结构抗疲劳的应力阈值，精准确定各类燃油管路的疲劳极限是发动机结构疲劳强度设计的重要依据。因此，研究燃油管路的疲劳极限测试方法具有重要意义。

疲劳失效是影响飞机和发动机金属结构安全性和使用寿命的主要因素。崔德刚等[1]指出贯穿全飞行器生命周期的5 个任务，才能够为飞机结构疲劳和完整性提供多道保障。刘斌超等[2]分析了飞机金属结构疲劳问题的特点，总结了疲劳分析方法的三种思路。林建鸿等[3]总结了相关的适航规章在不断吸取疲劳破坏事故经验教训的过程中逐步完善的演变经验，其中包括以安全寿命为理念的疲劳设计分析。潘陆原等[4]对飞机高压管路系统动态特性的研究方法及其关键技术进行了论述，耦合振动产生的交变载荷是管路疲劳失效的重要诱因。

在疲劳的试验研究方面，国内外许多机构和学者对材料级疲劳极限试验方法进行了研究，形成了相关的试验测试标准[5-6]，并在此基础上研制了多种疲劳试验控制设备[7-9]，对管路这类非标试验件提出了不同的疲劳的试验方法。常龙生[10]针对飞机液压管路的疲劳试验方法进行了论述，对试验参数、试验方法、试验数据处理等方面提出了参考性的建议。程小勇[11]利用振动台，采用共振测试的方法对液压管路进行了疲劳试验。吴云峰等[12]对管路焊缝结构进行了疲劳试验，并通过扫描电镜、金相分析等对其失效模式进行了分析。张凌云等[13]探究了平衡铅块对航空导管旋转弯曲疲劳试验的影响。韦东豪等[14]以气路部件整体作为疲劳试验对象，引入一种气路静电监测技术对航空发动机状态进行了在线监测。Bai Xin 等[15]在蒙特卡罗模拟的基础上，提出了一种在大散射数据下，测量和估计概率疲劳极限的新方法。Mahmud等[16]提出了一种新的基于控制图概念的疲劳寿命概率评估方法，对考虑散射和不确定因素的疲劳寿命结果的概率解释具有实用价值。

目前，航空发动机燃油管路的材料、管径、工作压力等与飞机其他管路有所差异，疲劳极限试验技术和相关参考数据仍然匮乏。本文研究了管路旋转弯曲疲劳试验方法，获得了航空发动机典型燃油管路结构在空管状态和充压状态下的疲劳极限和S-N曲线，并建立了燃油管路概率疲劳极限测定与评估的方法，为航发燃油管路应力严苛值设计提供参考。

1 管路旋转弯曲疲劳试验

1.1 发动机燃油管路试验件

试验件选取某型发动机燃油导管的一段典型结构，它由导管、接口（焊接锥口）以及外套螺母组成，如图1 所示。直管外径为25.4mm，壁厚为0.78mm，根据航空工业标准HB 6442—1990[17]，该管径对应的试验件管长l为305mm，材料为ANSI 321不锈钢，材料参数见表1。其中，接口与直管采用氩弧焊焊接，焊缝宽度约为3mm，每件的焊缝应经过射线探伤检查合格。

表1 燃油导管材料参数Table 1 Material parameters of fuel tube

图1 燃油导管试验件示意图Fig.1 Schematic diagram of fuel tube specimen

1.2 旋转弯曲疲劳应变监测方法

旋转弯曲疲劳试验原理是将管路一端固定，另一端连接在偏心转盘上，试验前，首先在偏心转盘端施加某一初始挠度，这样即可在另一个固定端产生弯曲应力。驱动偏心转盘转动后，即在管路试验件固定端截面处产生360°循环的弯曲交变应力。

上述原理的实施可以在旋转弯曲疲劳试验机上进行，如图2所示。将试验件两端通过外套螺母安装在试验机座上，用力矩扳手以HB 6586—1992[18]规定的最小拧紧力矩进行拧紧。试验机配有压力油源系统，管路试验件两端分别连接固定端和偏心转盘后，就形成了密封的油路，该设备可实施不同直径管路在0～4000r/min、0～60MPa范围内某一恒定转速和压力下的持续试验，试验件疲劳破坏时可自动卸压停机保护。本试验设置油路的压力至燃油系统的工作压力均为13.5MPa，模拟实际燃油管路充压状态。

图2 导管旋转弯曲疲劳试验机Fig.2 Rotating bending fatigue machine of tubes

当试验机旋转后由于偏心转盘惯性作用，管路上的弯曲应力并不等于初始挠度下的静态应力，因此管路的应力水平应以实测值为准。为了监控偏心旋转在管路上产生的实际应力，在固定端一侧管路表面（靠近焊缝约5mm处）上沿着导管的轴向粘贴三路单向应变片，粘贴方案如图3 所示。其中，一路连接试验机控制器里的应变仪，用于监测试验件疲劳循环次数。另外两路应变连接至DEWEsoft动态应变采集仪，用于监测试验件在旋转弯曲疲劳过程中的实时应变：ε1代表管路上表面轴向应变，ε2代表管路侧面轴向应变，两者沿着管界面相互垂直。这两路应变还可以避免导管的轴向安装应力。试验前，先手动旋转一圈调整两路应变接近一致，避免安装应力。

图3 应变片粘贴截面图和管路应变片粘贴位置Fig.3 Strain gauges on the cross-section and their pasting positions

1.3 非对称应力分析与修正

根据旋转弯曲加载试验原理，导管的固定端一侧外表面处的最大轴向应力是拉伸应力（由内压引起）和弯曲应力的叠加。对于空管而言，由内压引起的拉伸应力为零，只需考虑由偏移量引起的弯曲应力，理想情况下管道外表面为幅值大小相同的对称应力。对于空管，当εmax=-εmin时，应力比R=- 1，为对称循环载荷，实测应变结果如图4（a）所示。但是，对于充压导管，其内部恒定压力给导管轴向带来的拉伸应力，导致试验应力为非对称循环载荷，实测应变结果如图4（b）所示。

图4 管路弯曲疲劳过程中实测的应变—时间曲线Fig.4 Measured strain-time curve during tube bending fatigue process

针对充压导管出现的非对称循环载荷，取应变峰值的平均值作为试验应变值，并且充压试验应力需要进行应力修正，进而得到充压试验平均应力水平。试验中在应力幅给定的情况下，平均应力与应力比R有如下关系。

式中，Sm为平均应力；Sa为应力幅。

不同应力比R下的结构疲劳极限σr是不同的，工程上一般采用统应力比R=- 1（对称循环）下的S-N曲线表示结构疲劳应力—寿命关系，因此需要对非对称载荷下的循环应力进行应力修正。目前，常用的应力修正经验模型有Gerber公式[17]

式中，S-1为应力比R=-1 时的等效应力；St为静载下的拉伸破坏强度。

1.4 升降法测疲劳极限

升降法主要用于测定材料在指定循环周次下的疲劳极限，它以单点试验法为基础。如图5所示，单点试验法假定试样在指定循环基数N0下，疲劳极限σr位于发生相反试验结果（破坏与越出）的应力水平σi和σi+1之间。图5中，“破坏”表示试样在该应力水平下，未经历N0次循环即发生断裂；“越出”表示试样在该应力水平下，经历了N0次循环且未发生破坏。σi表示第i级应力水平，σi+1表示第i+1 级应力水平。

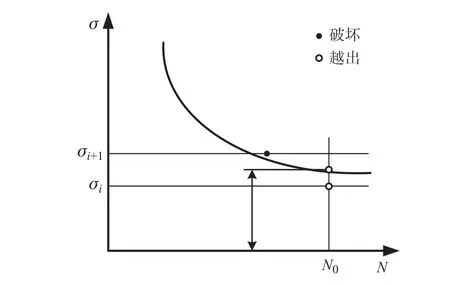
图5 升降法中的单点试验示意图Fig.5 Single point test in the up-down method

若两个应力水平之间差值很小（如小于σi的5%），可以近似取σi和σi+1的平均值作为近似疲劳极限。

当重复进行上述操作时，就会得到一系列“破坏”“越出”试验数据，进而求得一组具有同一目标循环基数下的疲劳极限值σri。升降法即以此为依据进行试验，最终利用统计分析方法对σri进行数据处理，即得到待求解的目标疲劳极限σr。

本次燃油管路旋转弯曲疲劳试验升降法的具体流程如图6所示，指定循环基数N0=1×107次。首先进行预试验，选择一个较高的初始应力水平σ0，并测试获得初始应力水平下的疲劳寿命。后一件试验应力水平视前一件试验结果（破坏还是越出）而定，若某一试验件在某应力水平σi的作用下未达到循环基数N0，就发生破坏，则下一次进行的试验件需要在更低的应力水平σi+1=σi-Δ下进行试验；反之，则应提高应力水平σi+1=σi+Δ。如此反复，当试验件达到规定件数要求时（有效数据达到15件），停止试验。

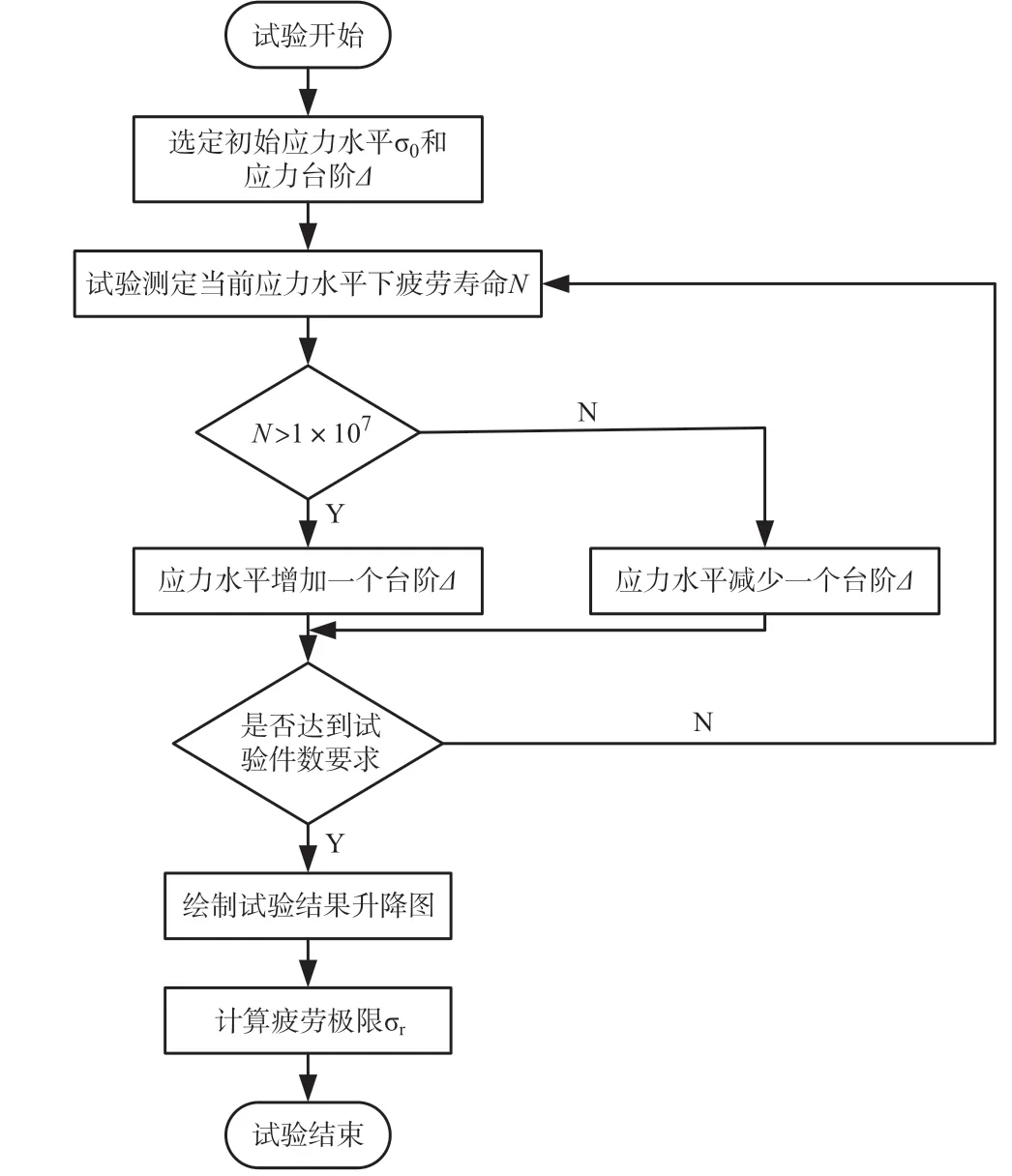
图6 旋转弯曲疲劳试验升降法流程Fig.6 Flow chart of the up-down method for rotational bending fatigue test

试验前采用应变片法对试验机进行调零，即控制管路外套螺母拧紧前后，试验机旋转头座旋转一周，应变采集系统微应变读数接近且在零值左右，以保证试验件两端无应力安装及同轴度。在试验控制软件中设置工作转速为2000r/min（33.33Hz），试验过程中，每隔1 × 106次记录一次应变数据，检查应变是否正常。当试验件发生疲劳断裂或达到规定试验次数时，停止试验，并记录试验件断裂次数。

2 疲劳寿命试验结果与分析

2.1 疲劳破坏位置

空管进行旋转弯曲疲劳试验完成后发现，其疲劳失效形式（破坏）为截面的整体断裂，如图7（a）所示，断裂位置均沿着试验件固定端处的焊缝周向，裂纹源为外表面。越出试验件经过107次循环而未发生断裂，并且试验结束后，检查试验件外观无明显变化，探伤固定端也无微裂纹，如图7（b）所示。

图7 疲劳试验后的空管试样Fig.7 Empty tube specimen after fatigue test

管内充压状态（13.5MPa）下疲劳试验件未越出时，不会直接发生截面整体断裂，而是在固定端焊缝位置处出现泄漏现象，如图8（a）所示。试验机自动停机检查后，发现管路焊缝的周向局部有贯穿裂纹。越出试验件经过107次循环而未发生泄漏或疲劳破坏，并且试验结束后，检查试验件外观无明显变化，探伤固定端焊缝无微裂纹，如图8（b）所示。

图8 疲劳试验后的充液导管试样Fig.8 Pressurized tube specimen after fatigue test

2.2 升降图

空管旋转弯曲疲劳试验以172MPa 应力水平为初始应力，应力台阶Δσ为8MPa，升降法疲劳试验结果见表2。

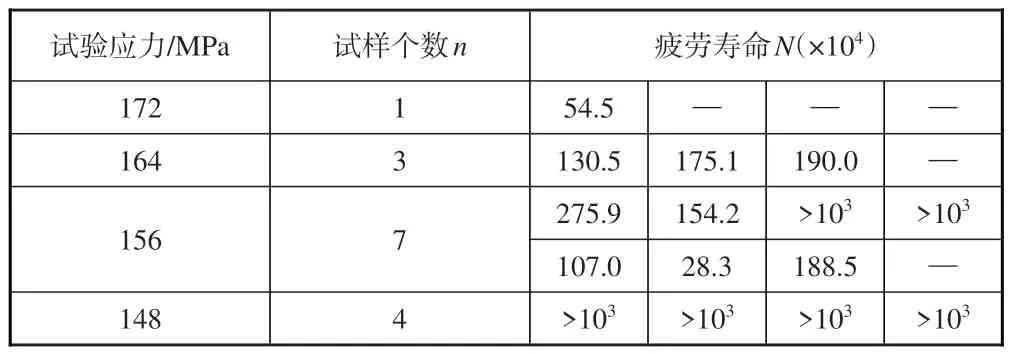
表2 空管旋转弯曲疲劳寿命试验结果Table 2 Fatigue life results of the empty tube rotating bending test

按照上述试验结果，为了避免初始应力选取较大对试验结果造成影响，根据升降图，以试验件第一次在相邻应力水平出现相反试验结果开始将数据进行配对[19]，为了将所有试验数据配对，需要继续补做试验，绘制得到空管旋转弯曲疲劳试验升降图如图9 所示。图9 中，实圈点表示“破坏”，代表试样发生断裂，疲劳寿命小于1×107次；空圈点表示“越出”，代表试样经过指定循环未发生破坏，疲劳寿命大于1×107次。

图9 空管旋转弯曲疲劳试验闭合式升降图Fig.9 Up and down diagram for the empty tubes rotating bending fatigue test

在图9 中，试验件3～16 以及试验件2 共15 个试验数据为有效数据。将有效数据进行配对，共7对，列于表3中，表中σri表示σi和σi+1的算数平均数。

表3 空管升降图中的应力水平配对Table 3 Matching of stress levels in the empty tube rotation bending fatigue test

采用相同方法处理充压（13.5MPa）管路的旋转弯曲疲劳试验数据，由于充油管路受到非对称循环载荷，为了统一试验结果便于后续进行对比研究，需要对试验应力进行修正。本文采用Gerber 公式对试验应力进行修正，见式（2），对应的疲劳寿命试验结果列于表4。

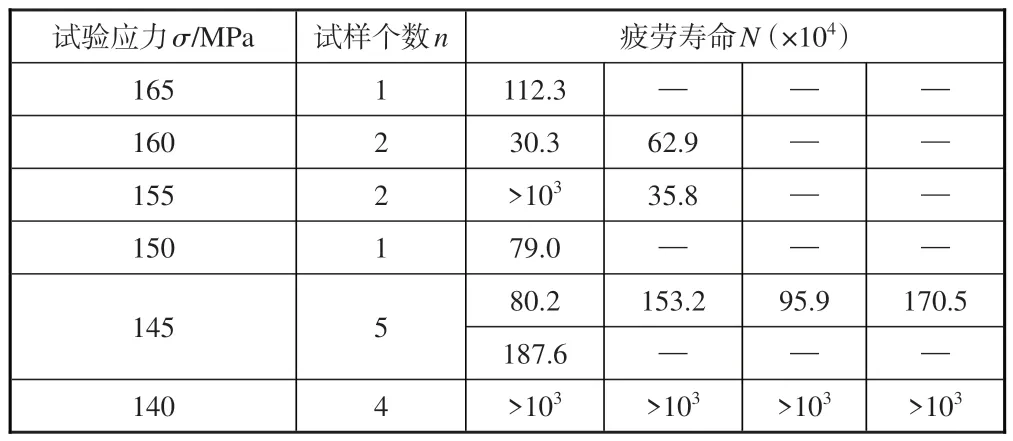
表4 充压管路旋转弯曲疲劳试验升降法试验结果Table 4 Fatigue life results of tube rotating bending test

根据上述试验结果，绘制得到充压管路旋转弯曲疲劳试验升降图，如图10所示。试验件2～15以及试验件2共14个试验数据为有效数据。将有效数据进行配对，共7对，列于表5中，表中σri表示σi和σi+1的算数平均数。

表5 充压管升降图应力水平配对Table 5 Matching of stress levels in the pressurized tuberotation bending fatigue test

图10 充压管路旋转弯曲疲劳试验升降图Fig.10 Up and down diagram for the pressurized tubes

2.3 幂函数型S-N曲线

燃油管路的S-N曲线，在工程的疲劳寿命预估中具有重要的作用。由于上述升降图数据在部分应力水平下的样本点不足，本文在升降法试验的基础上继续补充试验。补充试验的应力水平分为三组，空管补充试验的寿命结果见表6。

表6 空管旋转弯曲疲劳试验补充试验结果Table 6 Supplementary test results of the empty tuberotating bending fatigue

将升降法测得的疲劳极限数据点和成组试验法测得的有限疲劳寿命数据点合并在一起，然后进行航空发动机燃油管路S-N曲线的拟合，工程常用幂函数型经验公式作为S-N曲线的描述

SαN=C（4）

式中，α与C均为材料常数。对式（4）两边同时取对数可得

lgN=-α⋅lgS+ lgC（5）

根据所有空管的旋转弯曲疲劳寿命试验数据，并结合式（5）可以拟合得到空管的S-N曲线表达式为

lgS=- 2.29lgN+ 2.19 （6）

将式（6）参数代入式（4）画出的幂函数S-N曲线和试验结果如图11 所示。其中，α与C两个参数的相关系数均为0.94，拟合效果良好。

图11 空管的S-N曲线Fig.11 S-N curve of the empty tube

同理，为了得到充压导管的S-N曲线，按照上述方法，继续补做三个应力水平下的充压导管旋转弯曲疲劳试验，补充试验结果见表7。进而拟合得到充压燃油导管（13.5MPa）的S-N曲线为

表7 充压管旋转弯曲疲劳试验补做试验结果Table 7 Supplementary test results of the pressurizedtube rotating bending fatigue

lgS=- 1.43lgN+ 2.15 （7）

将式（7）参数代入式（4）画出充压燃油导管的幂函数S-N曲线和试验结果如图12所示。其中，α与C两个参数的相关系数分别为0.81 和0.86（略低），这是由于充压导管的每一级应力水平上的成组法试验的试验件数较少，且疲劳寿命分散性大。式（7）的拟合效果仍然满足工程应用要求。

图12 充压(13.5MPa)管的S-N曲线Fig.12 S-N curve of the pressurized tube (13.5MPa)

3 概率疲劳极限分析

3.1 概率疲劳极限分析方法

疲劳试验寿命受多种随机因素的影响，其同一种应力水平的寿命结果往往会有一定的分散性。因此，对寿命结果进行统计分析就显得尤为重要。概率疲劳极限是指在指定疲劳寿命下，疲劳强度的概率估计值[16]。传统方法的疲劳极限实际为“在指定循环基数N0下，试样的中值（50%的存活率）疲劳强度估计量”[19]。

正态分布在工程实践中应用广泛，在小子样升降法中，假设疲劳极限遵循正态分布，则其频率函数可以写为

式中，σr为个体（试样）疲劳极限；μ为母体中值疲劳极限；s为母体疲劳极限标准差。

根据极大似然估计原理，当应力σri服从正态分布时，可以取子样平均值作为母体中值的估计量，μ和s表达式分别为

式中，n为有效数据个数；m为配对应力水平个数；σi为第i级应力；vi为第i级应力水平下有效数据个数；np为配对总数；σri为σi和σi+1的算数平均数；ni为对应应力水平下对子个数。

将试样在任意应力水平σi下，越出107次循环的概率记为P（存活概率），置信度表示待测值以一定概率落于真实值的程度。在小子样升降法中，假设疲劳强度服从正态分布，则在任意存活概率P下的疲劳极限σP、某一置信度γ下的单侧疲劳极限取值σγ以及联合考虑P与γ的单侧疲劳极限取值σP-γ可以按照下列公式计算[20]。

式中，ZP为标准正态分布在存活概率为P时的百分位值；t1-γ(k-1)为显著水平为1-γ、自由度为k-1 时的t分布函数值。

依据上述公式，对升降法疲劳试验数据进行处理，即可得到给定存活概率和置信度下的疲劳极限，进而可以求得试样在指定疲劳寿命基数N0下的概率疲劳极限。

3.2 空管概率疲劳极限

根据空管疲劳极限试验数据，可以求得空管状态下管路疲劳极限均值和标准差。标准差是用来表示数据分散性的参数。但标准差只与数据偏离平均值的大小有关，而与每个个体的数值大小无关，因此，需要引入变异系数Cν用以表示个体数据偏离平均值的程度，即

当σr，s，n满足式（17）条件时，以子样疲劳极限来代替母体疲劳极限，有γ的置信度，并且相对误差不超过±δ。δ一般取5%。在给定相对误差δ与置信度γ的情况下，可以得到对应子样中最少观测个数n，也可通过查找置信度γ、误差限度δ与最少有效试样个数[19]。结合上述分析，将升降法测得的疲劳极限数据点和成组试验法测得的有限疲劳寿命数据点合并在一起代入式（9）和式（10），可以得到空管的中值疲劳极限σr= 154.3MPa，标准差为3.9MPa。

由于本文将升降法试验数据进行了配对，即相当于人为减小了数据的分散性，根据成对数据估算出的疲劳极限，与原样本母体（无配对）标准差的无偏估计会存在一定的误差[21]。表8 分别讨论了采用配对和无配对两种处理方法时，计算出存活率为50%时疲劳极限标准差估计，供工程参考。

表8 配对处理对的疲劳极限估计的影响Table 8 The effect of pairing treatment on fatiguelimit estimation

上述结果为中值疲劳极限，即存活概率为50%，该概率不能保证结构在使用过程中充分安全。因此，需要在考虑存活概率与置信度基础上，进行结构的概率疲劳极限分析。根据式（13）可以求得典型存活概率P和置信度γ下的概率疲劳极限σP-γ估计值，以评判不同应力状态下管路应力严苛程度，见表9。表中第4列为t分布函数的数值，由显著度1-γ和自由度确定，为配对数减1（本文的疲劳数据配对数为7）。

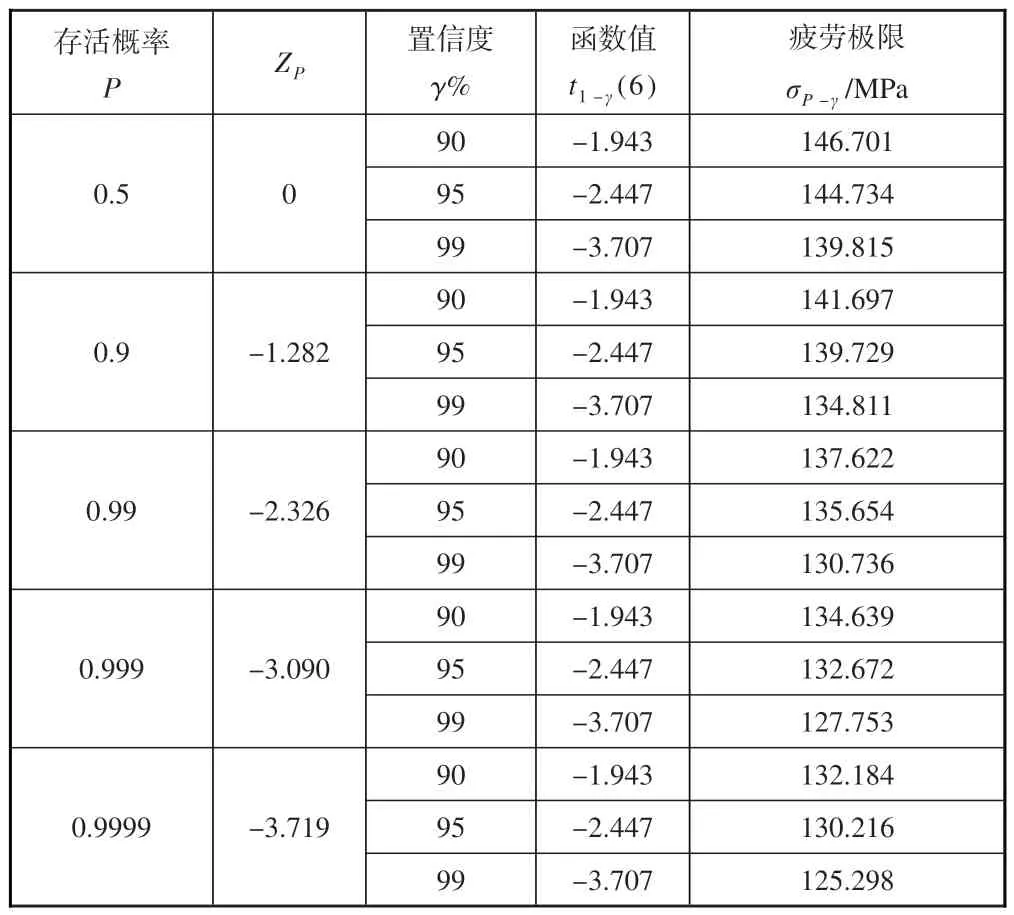
表9 空管典型概率下的疲劳极限值Table 9 Fatigue limit stress under typical probability of empty tube

3.3 充压管概率疲劳极限

同理，根据充压管路疲劳极限试验数据，对充压管路进行概率疲劳极限分析。充压（13.5MPa）状态下，由于循环应力非对称，基于应力修正方法以及式（9）和式（10）得到中值疲劳极限为147.5MPa，标准差为7.07MPa。求得典型存活概率P和置信度γ下的概率疲劳极限σP-γ，见表10。

表10 充压管路典型概率疲劳极限值Table 10 Fatigue limit stress under typical probability of pressurized tube

4 结论

本文开展了航空发动机燃油管路在空管和充压两种状态下的旋转弯曲疲劳试验研究，得到如下结论：

（1）改进了导管旋转弯曲疲劳试验方法，采用两路应变方法，监测了偏心旋转过程中由惯性引起的动态应力，同时还避免了安装应力，基于Gerber 模型对内压导致的非对称循环载荷进行了应力修正。

（2）采用升降法完成直径为25.4mm、壁厚为0.78mm、ANSI 321 材料的燃油管路结构旋转弯曲疲劳极限试验测定。结果表明，空管时，燃油导管的中值疲劳极限（50%的存活概率）为154.3MPa；充压（13.5MPa）状态下，由于循环应力非对称，基于应力修正方法得到中值疲劳极限为147.5MPa。

（3）获得了两种工况下管路疲劳失效形式的差异。空管为截面完全断裂破坏，充压管为泄漏破坏，破坏位置均在固定端的焊缝处。结合已有试验数据，继续补做高应力水平的疲劳寿命试验，基于幂函数模型分别获得了燃油管路在空管和充压两种状态下的S-N曲线。

（4）采用统计方法对管路结构旋转弯曲疲劳极限进行了概率计算以及可靠性评估，计算得到的管路结构给定存活率和置信度下概率疲劳极限值σP-γ，可以作为不同可靠度设计要求下的管路应力严苛值参考。