基于CNLS-MMD的孪生混合网络四旋翼飞行器故障诊断方法

张雅婷，杨蒲，孟宪锋，陆宁云，文琛万

1.南京航空航天大学，江苏 南京 210016

2.航空工业西安飞行自动控制研究所，陕西 西安 710065

四旋翼飞行器是一种能实现垂直起降的非共轴式多旋翼飞行器[1]，具有结构简单、成本低和操作简便等优点，广泛应用于军事、民用生产和消防等不同领域。由于受工作环境恶劣及部分零部件结构损伤的影响，四旋翼飞行器不可避免地会出现各种故障，对人们的生产生活造成巨大的经济损失。 因此，研究四旋翼飞行器的故障诊断方法，对保证四旋翼飞行器的安全性和可靠性具有重要意义。

四旋翼飞行器通常采用对其中某零件进行仿真破坏的方法来获取其结构损伤性的故障数据，但在实际操作中，由于四旋翼飞行器飞行环境复杂多变、飞行器结构损伤性失效数据尺寸较小等，采集到的有效数据样本非常有限。当下以信号处理与深度学习为核心的主流故障诊断方法大多依赖于完整的故障样本进行故障诊断，在小样本情形下，往往难以获得充足的训练数据来构建有效的深度学习模型[2]，以往性能良好的故障诊断算法也会出现诊断准确率低、泛化能力差等问题。如何在少量样本条件下提高故障诊断精度，改善模型泛化能力，降低过拟合，可以归结为小样本学习问题[3]。在小样本条件下进行故障诊断是当今研究热点之一。其中，元学习中基于度量学习的孪生网络在小样本问题中表现出一定的优越性[4]，现已取得不少研究成果。朱瑞金等[5]提出了一种基于卷积孪生网络的故障诊断方法，在小样本条件下实现变压器的故障分类，但没有明确解决多工况数据诊断问题。徐卓飞等[6]针对在小样本和强噪声条件下对滚动轴承进行故障诊断的问题，提出了一种基于孪生网络的诊断模型。高浩寒等[7]针对深度神经网络在小样本条件下准确率低的问题，提出了基于孪生神经网络的小样本故障诊断方法，建立了孪生子网络提取低维特征，利用距离度量得到特征的相似度作为分类依据。以上文献的研究方法虽在特征提取与故障诊断准确率两个方面取得了较好的效果，但也存在明显的不足：在特征提取方法上存在局限性，并不能充分挖掘时序数据的相关性；故障数据单一化，方法泛化能力较差。

结合上述研究，针对四旋翼飞行器结构损伤性故障复杂工况多样、有效故障数据有限等问题，本文建立了一种基于CNLS-MMD 孪生混合网络四旋翼飞行器故障诊断模型，采用卷积神经网络和长短时记忆网络构建混合模型对小样本数据进行特征提取，SHNN 模型扩充数据样本。通过最大均值差异来度量数据样本对的差异，计算不同样本对的特征距离实现样本分类。最终实现在小样本、多工况条件下对四旋翼飞行器结构损伤性故障的诊断。

1 CNLS-MMD孪生混合网络模型

1.1 孪生神经网络

孪生神经网络（SNN）[8]是一种衡量特征相似度的小样本学习方法。SNN的网络结构主要由两个网络结构完全相同的子网络和一个相似度计算模块组成，如图1 所示。从训练集中随机抽取两个样本数据分别输入子网络，当两个样本为同类样本时标签为1，反之则为0。经过两个权值共享子网络的相关特征提取之后，由相似度模块计算样本数据之间的相似度距离，当其距离越近，二者数据的相似度越高。最终SNN 通过对比损失函数评价两个样本的相似程度，通过同一特征空间下样本数据的相似度判断样本是否为同一类别，实现对SNN模型的训练。

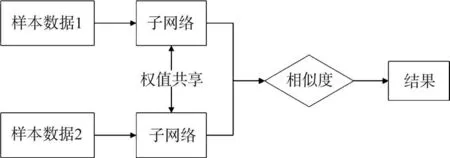
图1 孪生神经网络结构图Fig.1 Structure diagram of SNN

在SNN 训练阶段，为了减小相同样本之间的损失值，增大不同样本之间的损失值，采用对比损失函数来优化模型的训练目标，如式（1）所示

式中，ε为孪生网络的共享参数；ai和aj为输入数据样本对；b为两个样本对判别是否为同类的结果，b= 1 表示二者为同类，b= 0 表示二者为不同类；K表示模型训练阶段的batch size；m为样本之间距离的最大值。在计算损失值时，当只计算不相似样本距离在0～m范围的样本对，若样本相似距离超过m时，表示样本间的损失值很低，被视为0。反之，只考虑相似样本对时，当相似距离较大时，需要增加损失函数值，实现对模型内部参数的优化，提高模型性能。

利用 SNN不直接学习数据的特征，而是通过数据之间的相似性来解决分类问题的特点，降低了SNN模型对数据数量的要求。同时，通过把原本的训练样本转换为样本对的过程在一定程度上起到了扩充样本数量的作用，增强了样本数据。

1.2 卷积神经网络

卷积神经网络（CNN）[9]因拥有强大的特征自主提取的能力，广泛应用于图像识别和故障诊断等领域。

卷积层由多个卷积核构成，主要作用是提取信号的特征。若卷积神经网络的层数为n，那么卷积层的运算公式如下

式中，ynm表示网络的输出；Xnm表示第m个卷积核；xnm是偏置值；Nj为输入数据的集合；f(∙) 为自主选择的激活函数。

池化层的主要作用是对提取出的特征进行采样来降低纬度，减少计算量，加快训练速度。

全连接层的主要作用是将池化层中展开的一维矢量输入，将前一层和该层的神经单元相连，从而获取全局信息[10]。

1.3 LSTM网络

长短时记忆网络（LSTM）是一种被改进的循环神经网络（RNN），其主要作用是改善RNN中出现的梯度消失和梯度爆炸问题[11]。相比于RNN，LSTM 网络结构多增加三个控制门和一个记忆门。在LSTM 单元中，门控机制主要分为输入门、遗忘门和输出门[12]。

LSTM 单元对信息的选择主要通过门控机制中的sigmoid函数和逐点乘法运算来实现，其计算过程主要如式（3）～式（7）所示。

输入门It的主要作用是决定t时刻输入值xt在上一时刻隐藏层输出Ht-1中保存的比例，其计算公式如下

式中，wxi为输入层到输入门的权重矩阵；whi为隐藏层到输入门的权重矩阵；bi为输入门的偏置；σ为sigmoid 激活函数。

遗忘门Ft的作用是处理上一刻的输入信息，选择哪些数据需要被丢弃，具体计算公式如下

式中，wxf为输入层到遗忘门的权重矩阵；whf为隐藏层到遗忘门的权重矩阵；bf为遗忘门的偏置；σ为sigmoid 激活函数。

输出门Ot的主要作用是与记忆单元Ct一起共同决定LSTM 单元的输出Ht。其中，记忆单元Ct由上一刻的记忆单元Ct-1和经历sigmoid函数、tanh函数共同处理的输入量xt计算可得，具体计算公式如下

式中，o和c为输出门和记忆单元；w和b为网络的权重矩阵和偏置；σ为sigmoid 激活函数；tanh 表示非线性激活函数；⊙表示向量的点乘。

1.4 最大均值差异

最大均值差异（MMD）最早提出时是用于双样本检测问题，用于判断两个分布是否相同[13]。MMD将两组分布数据集X和Y采用相同的映射函数f(∙)到同一样本空间中，计算不同分布在映射后的平均值差异。若数据集X和Y的大小为m和n，则MMD的表达式为

式中，f(∙) 为高斯核函数；H表示样本映射到同一样本空间再生希尔伯特空间（RKHS）。当MMD的值越小，则两个分布越相似，两个样本属于同一类别的概率越大，反之，MMD的值越大，两个样本属于同一类别的概率越小。

1.5 孪生混合网络模型搭建

本文提出了基于CNLS-MMD 的孪生混合网络（SHNN）四旋翼飞行器故障诊断模型结构，如图2所示。模型由上下两个子网络和一个相似度计算模块三部分组成，在每个子网络中包含着一个1D-CNN模型和一个LSTM模型，并均连接一个全连接层。其中，1D-CNN模型主要由4个卷积层和4个池化层构成，按照式（2）自适应提取数据特征，且n取值为4，LSTM 网络由128 个神经元构成，按照式（3）～式（7），结合数据上下文信息进一步提取特征，结合二者共同完成SHNN 整体对输入样本数据的特征编码，提高了数据利用率。然后对经过网络模型编码后的特征矢量按照式（8）计算样本对的MMD，通过MMD 来衡量两个矢量间的相似度，实现输入数据样本标签的分类预测。

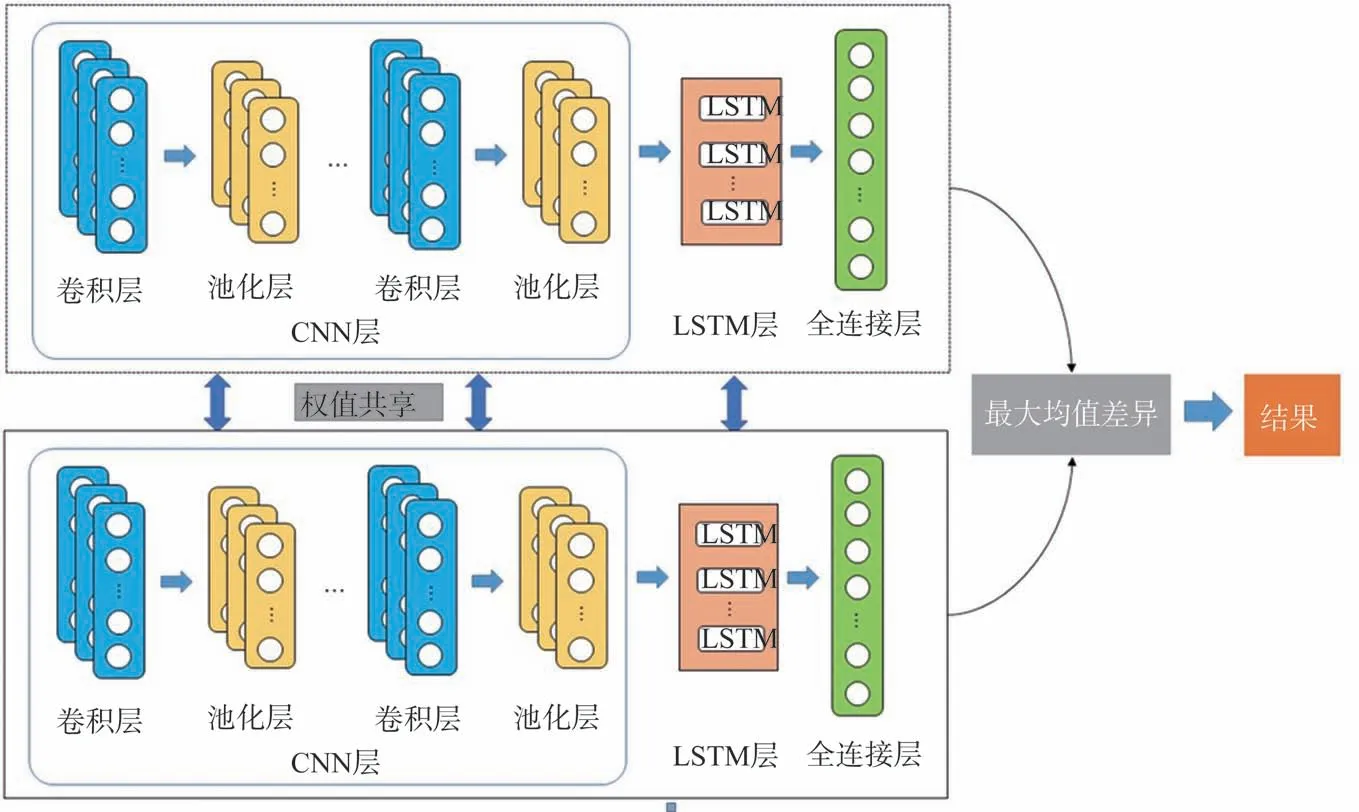
图2 SHNN模型结构图Fig.2 Structure diagram of SHNN model

1.6 故障诊断流程

基于CNLS-MMD的孪生混合网络四旋翼飞行器故障诊断流程由图3所示，具体操作流程如下。

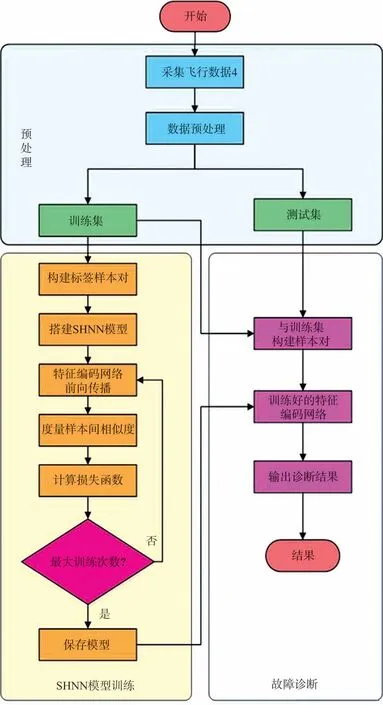
图3 模型故障诊断流程Fig.3 Model fault diagnosis flowchart

（1） 实验室开展了四旋翼飞行器飞行试验，采集了不同运行状态和不同失效情况下的飞行数据，将数据归一化和标准化后构造了模型训练集及测试集合。

（2）构建SHNN 模型（见图2），对模型中参数进行初始化。在训练数据集中每随机抽取两个故障样本构成一个样本对输入SHNN模型，训练SHNN模型中特征编码网络，输入输出标记形式为Dtrain={(ai,bi)}Ntraini=1，其中xi∈XT是模型的训练集输入数据；bi∈[0,1]为输入数据对应的标签。然后，按照式（1）计算比较损失函数值，通过迭代最小化孪生网络的损失函数值反向更新模型参数。当迭代次数为给定最大轮次时保存模型参数。

2 试验

2.1 数据集

本文采集的数据集为QBall-X4 四旋翼飞行器在实验室环境下采集的飞行数据。QBall-X4四旋翼飞行器如图4所示。四旋翼飞行器4 个电机分别产生F1、F2、F3和F4共4个升力，飞行器4个旋翼编号与电机编号顺序相同。

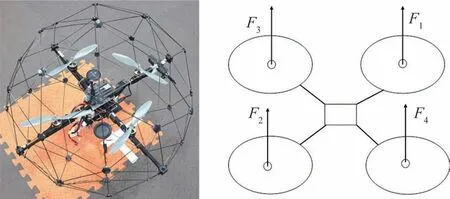
图4 四旋翼飞行器及其简图Fig.4 Quadrotor aircraft and its schematic diagram

试验以25Hz 频率采集了三种不同旋翼状态的飞行数据，分别是无故障、旋翼桨叶损伤故障和旋翼桨叶裂纹故障，其中旋翼裂纹故障有三个级别，依次是轻微、中等和严重；旋翼损伤故障从轻微到严重有4 个故障级别。四旋翼飞行器8种不同故障损伤如图5所示。

图5 四旋翼飞行器不同故障损伤图Fig.5 Damage diagram of different faults of quadrotor aircraft

在故障发生后，四旋翼飞行器的姿态角会发生较大幅度的摆动。四旋翼飞行器的3 号桨叶发生轻微断裂损伤时，发生故障时的四旋翼飞行器姿态角输出和无故障时的姿态角输出如图6所示。由图6（a）和图6（b）可得，相比于无故障的姿态角数据，发生故障后的无人机姿态角数据出现了明显的噪声，但通过肉眼很难对故障进行判别。本文将对采集的多旋翼无人机飞行数据进行分析处理，并建立相应的诊断模型以完成四旋翼飞行器结构损伤性故障诊断。

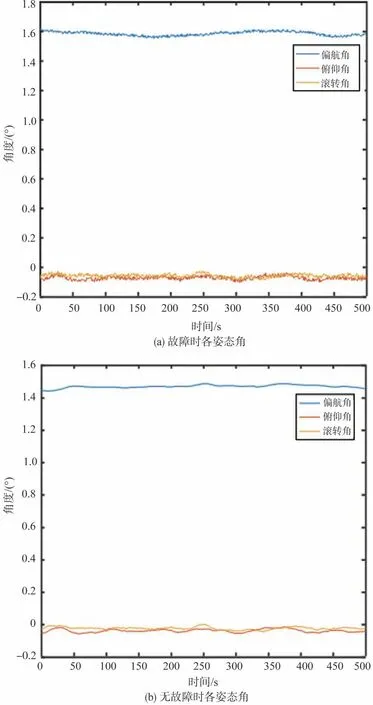
图6 四旋翼飞行器各姿态角输出Fig.6 Each attitude angle output of quadrotor aircraft

对飞行数据进行预处理，随机选取部分数据建立不同工况条件下的试验训练集和测试集。其中，训练集是分别在无负载条件下选择每种单一故障样本数为10、30、60、100和500 个的不同数据集。测试数据集由样本数均为500 个的三个不同工况的数据集组成。数据集具体划分见表1。

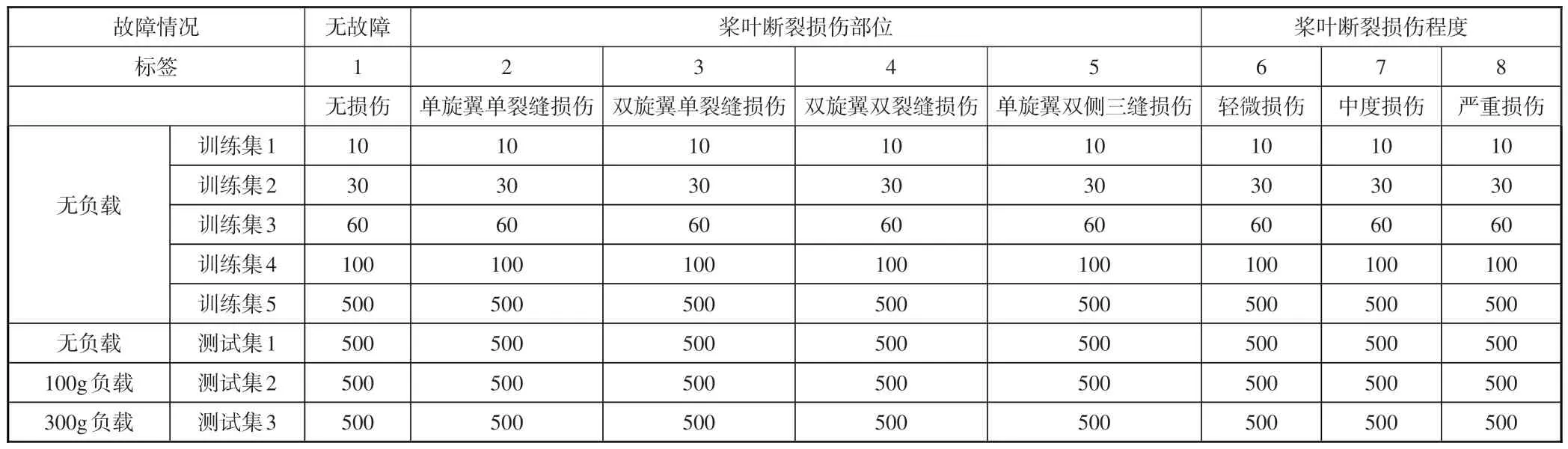
表1 数据集具体划分Table 1 Data set specific division

2.2 模型参数设置

本文在Ubuntu 18.04 操作系统下，采用Pytorch 搭建试验模型，SHNN模型中的CNLS网络主要由一个4层网络结构的一维卷积神经网络和128 个LSTM 单元组成。SHNN模型在训练时采用Adam 算法来进行参数优化，学习率设置为0.0015，最大迭代轮次为100 次。输入样本的尺寸为35 × 10，其中10 表示输入单时序的输入尺寸，35 表示处输入的总时序总数。模型的输出为长度为64 的一维矢量。SHNN模型的主要网络结构参数见表2。

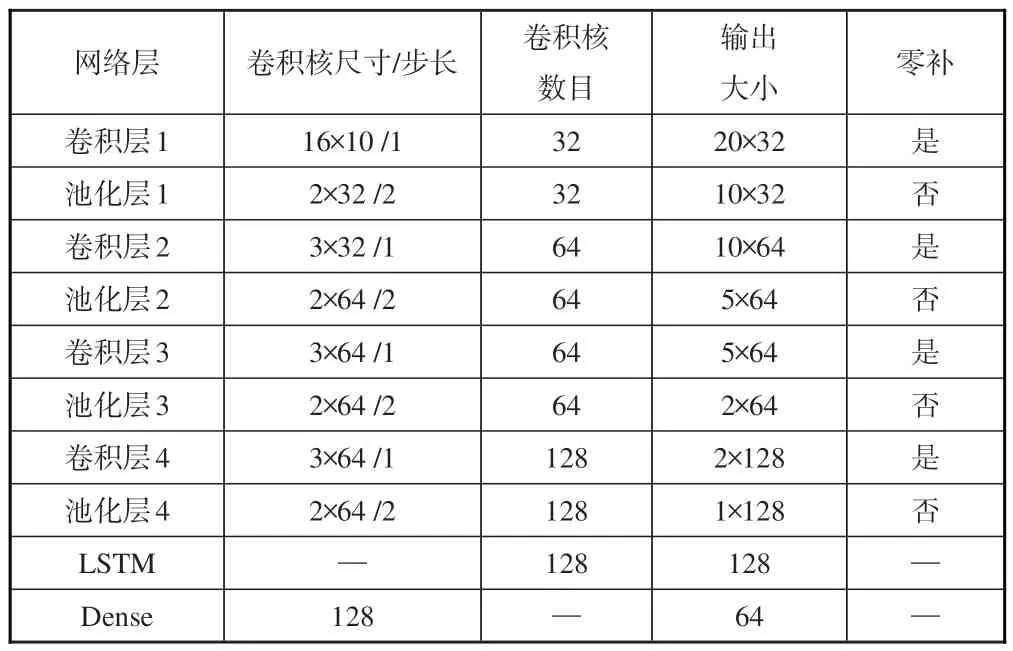
表2 SHNN模型主要网络结构Table 2 Main network structure of SHNN model

2.3 试验结果与分析

本文选取表1 中的无负载条件下5 个训练集作为模型的训练数据，选取无负载条件下的测试集1来验证模型的性能。SHNN模型的训练集准确率曲线和测试准确率曲线如图7所示。可以看出，SHNN 模型在不同训练集的准确率迅速达到了98%左右并趋于平稳，这表明了SHNN 模型在小样本的条件下可以依赖自身网络结构从样本中学习到有效信息。

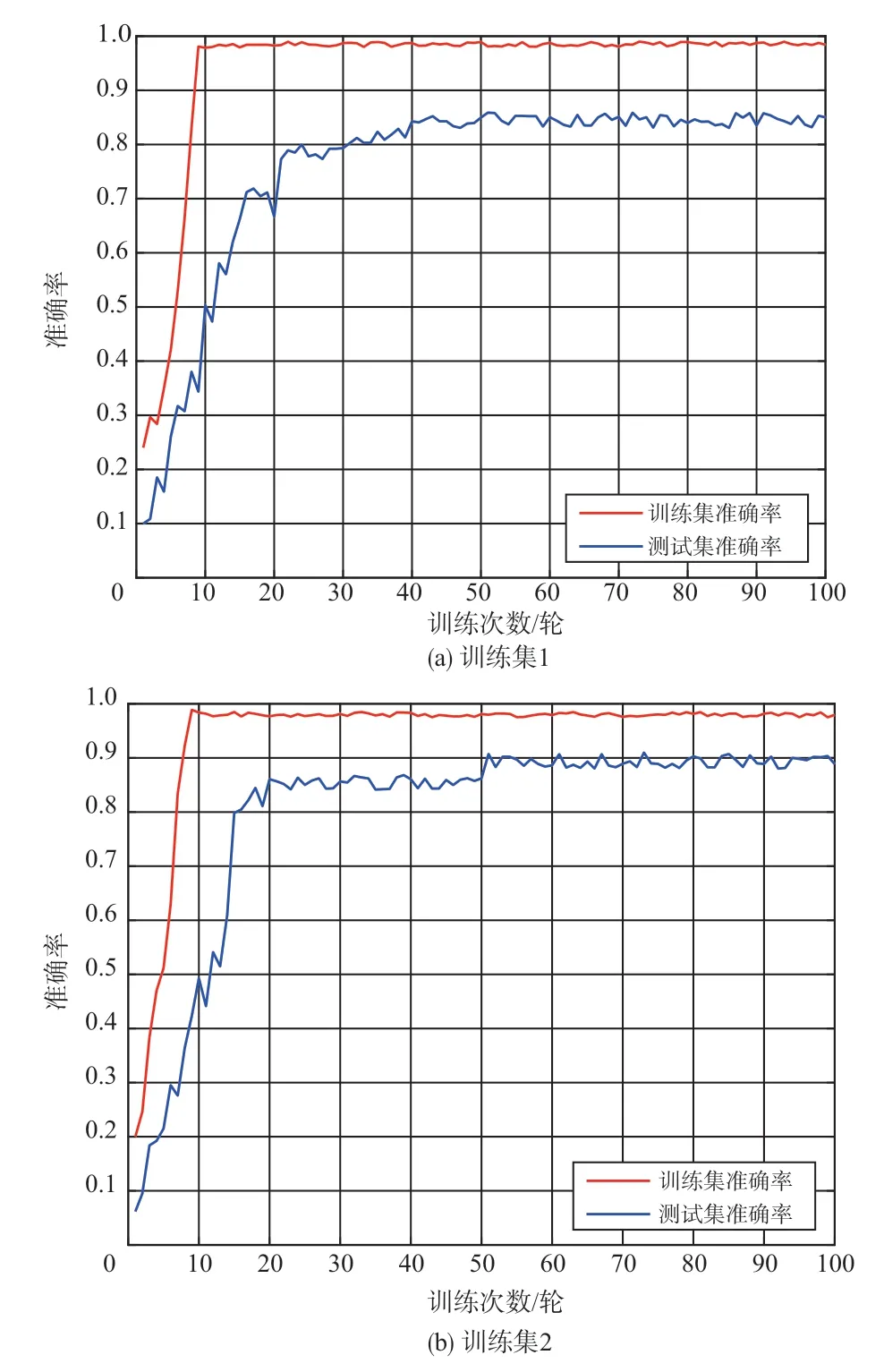
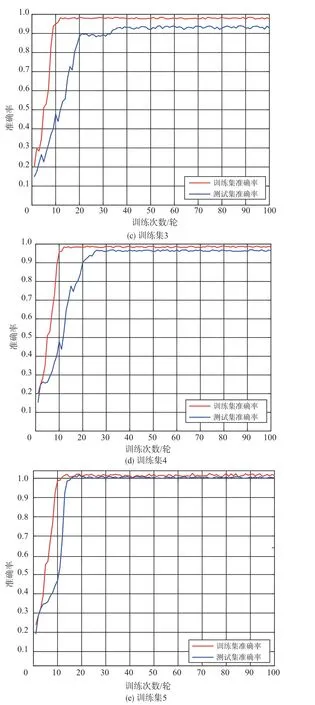
图7 不同训练样本数的训练集和测试集准确率曲线图Fig.7 Accuracy curves diagram of training set and test set under different training samples

由图7（a）中可知，SHNN 模型在测试样本规格为10个的条件下，测试集的准确率稳定在84%左右，远低于训练集的准确率，此时模型产生了较强的过拟合；在图7（b）中，样本规格增加到30个，SHNN模型在测试数据上的诊断准确率超过了90%，与图7（a）相比，模型过拟合问题得到了明显改善；在图7（c）和图7（d）中，随着训练集的规模不断增大，模型在测试集的准确率分别达到了 93%和 97%。直到图7（e），模型的训练集准确率和测试集准确率基本相同，实现了对四旋翼飞行器的故障诊断。总体而言，当样本数量不断增加时，SHNN模型的泛化能力逐渐提高，模型训练过程也更加平稳。

SHNN模型采用不同规模的训练集得到的模型在测试集1的诊断准确率如图8所示。可以看出，样本数量的增加对模型训练集准确率的提高效果显著，而且模型诊断准确率随样本数增加而逐渐提高。

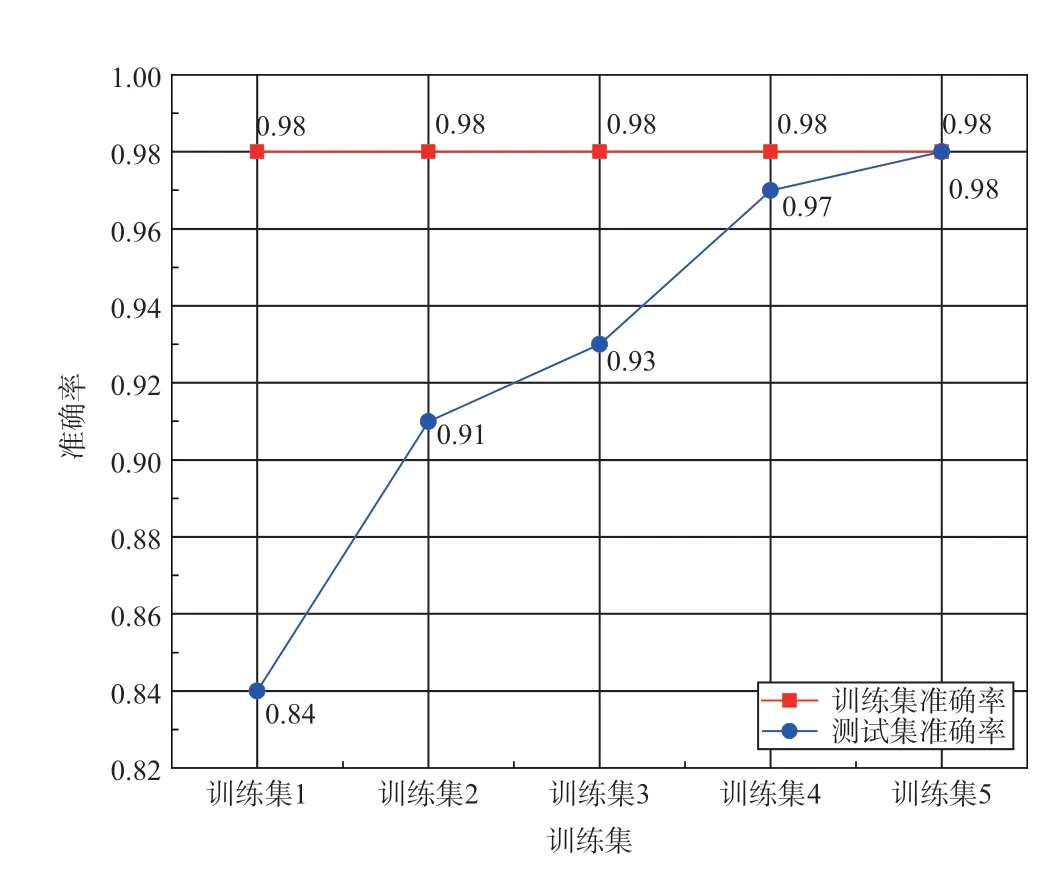
图8 SHNN在不同训练集下的训练集和测试集1的准确率Fig.8 SHNN’s accuracy of training set and test set 1 under different training sets

为了分析本文提出的SHNN中特征提取网络对故障模型故障诊断性能的影响，对比三种不同的特征提取方法：只使用1D-CNN 进行特征提取、只利用LSTM 进行特征提取和采用本文提出的CNLS网络进行特征提取。在不同的样本数的训练集下测试了各个特征提取方法的诊断准确率，结果见表3。

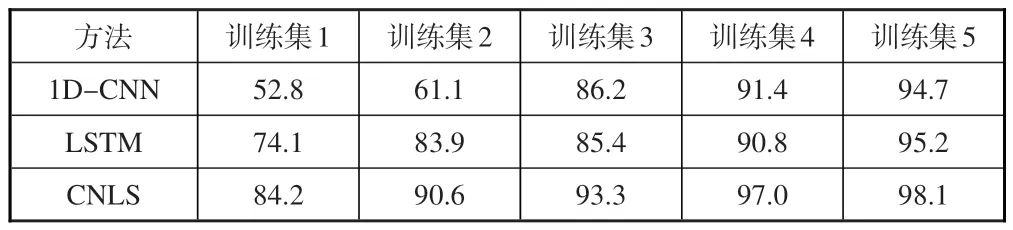
表3 不同特征提取方法的故障诊断准确率（单位：%）Table 3 Fault diagnostic accuracy of different featureextraction methods（Unit：%）

分析结果可得，每类样本数据量只有 10 个时，采用CNLS为特征提取网络的模型诊断准确率可达到84.2%，高于LSTM模型的诊断准确率（10.1%），而采用1D-CNN模型的诊断准确率只有52.8%。可以看出，在模型中的训练样本数特别少的情况下，1D-CNN 的特征提取能力最差。不同训练模型的诊断准确率均随着样本数量的增加而升高，但是在不同规模的训练样本条件下，本文提出的CNLS 网络作为模型的特征提取网络时，模型的准确率在不同样本规模的数据集下均达到84%以上，诊断准确率明显优于1D-CNN 和LSTM。这说明了本文所提CNLS 网络在数据特征提取上的优越性。

为了验证本文提出的模型中相似度度量方法对模型诊断的性能，在本文提出的孪生网络框架下，依次采用欧氏距离、余弦距离和 MMD 来度量样本对之间的差异。三种不同相似度度量方法分别在不同的数据样本规格下对模型诊断准确率进行验证，结果见表4。

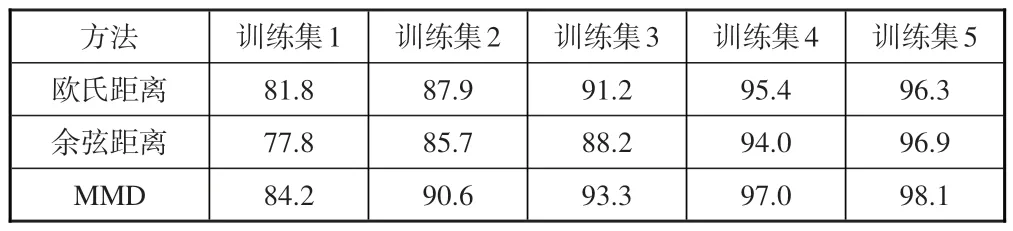
表4 不同相似度度量方法的故障诊断准确率（单位：%）Table 4 Fault diagnosis accuracy of different similaritymeasurement methods（Unit：%）

当样本量为10 个时，采用MMD 度量方式的模型诊断准确率为84.2%，远高于采用欧氏距离和余弦距离度量方式模型的诊断准确率。随着训练样本数量的增加，采用三种度量方式的模型的诊断准确率均有所上升。当采用训练集5进行训练时，采用MMD度量方式的模型诊断准确率为98.1%，同时比欧氏距离高出1.8%，比余弦距离高出1.2%。从整体来看，在不同规模的训练集下，采用MMD度量方式的模型诊断性能均优于其他两种相似度度量方法。

为了进一步验证SHNN模型在小样本条件下对飞行器故障诊断的性能，选择了不同子模型组合的孪生网络模型和原型网络作为对比方法。孪生网络使用1D-CNN作为模型的特征提取网络，以欧氏距离度量样本对之间的相似度。原型网络[14]是小样本学习方法之一，通过将训练数据集划分为支持集和查询集，计算待测样本与类原型之间的距离来完成最近邻分类。

三种方法采用不同样本规格训练集进行训练，分别使用相同工况的测试集1和两种不同工况的测试集2、测试集3进行验证分析与测试，诊断结果如图9～图11所示。由图9可得，在相同工况条件下，样本数量对识别准确率有明显的影响，随着样本数量的增加，不同模型的诊断准确率越高。但本文提出的SHNN 方法在5 种不同规格的训练集下，诊断准确率明显高于另两种方法，尤其是当训练样本数量设置为30个时，SHNN模型诊断准确率为90.6%，远高于孪生网络的69.2%和原型网络的71.3%。由图10 和图11 可得，飞行器负载变化越大，其故障诊断的准确率越低。面对不同样本数量的训练集，孪生网络和原型网络的诊断性能均较差，如当训练样本数量设置为10 个时，二者在两种工况下的诊断准确率均低于47%；当训练样本数量设置为500个时，二者在两种工况下的诊断准确率均低于73%。然而，本文所提出的SHNN模型在训练样本数量设置为10个时，两种工况下的诊断准确率分别为70.3%和66%；当训练样本数量设置为500个时，SHNN模型在两种工况下的诊断准确率分别为84.1%和89.1%，其诊断性能明显优于孪生网络和原型网络方法。

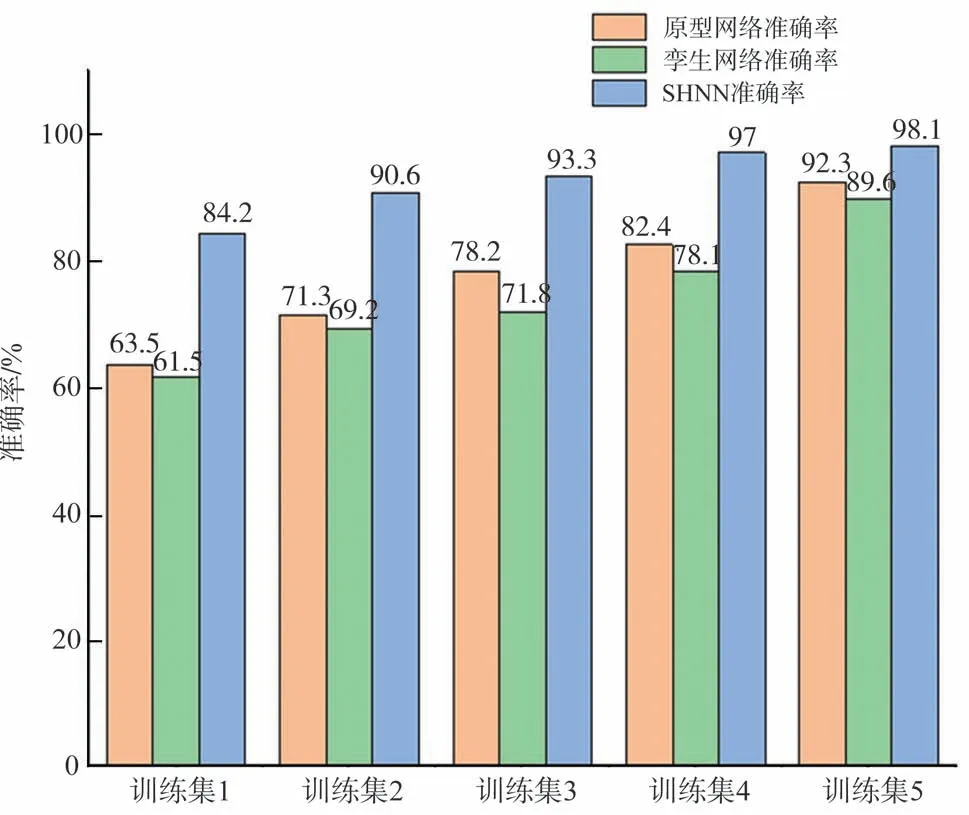
图9 各类故障诊断方法在测试集1诊断准确率Fig.9 Diagnostic accuracy of various fault diagnosis methods in test set 1

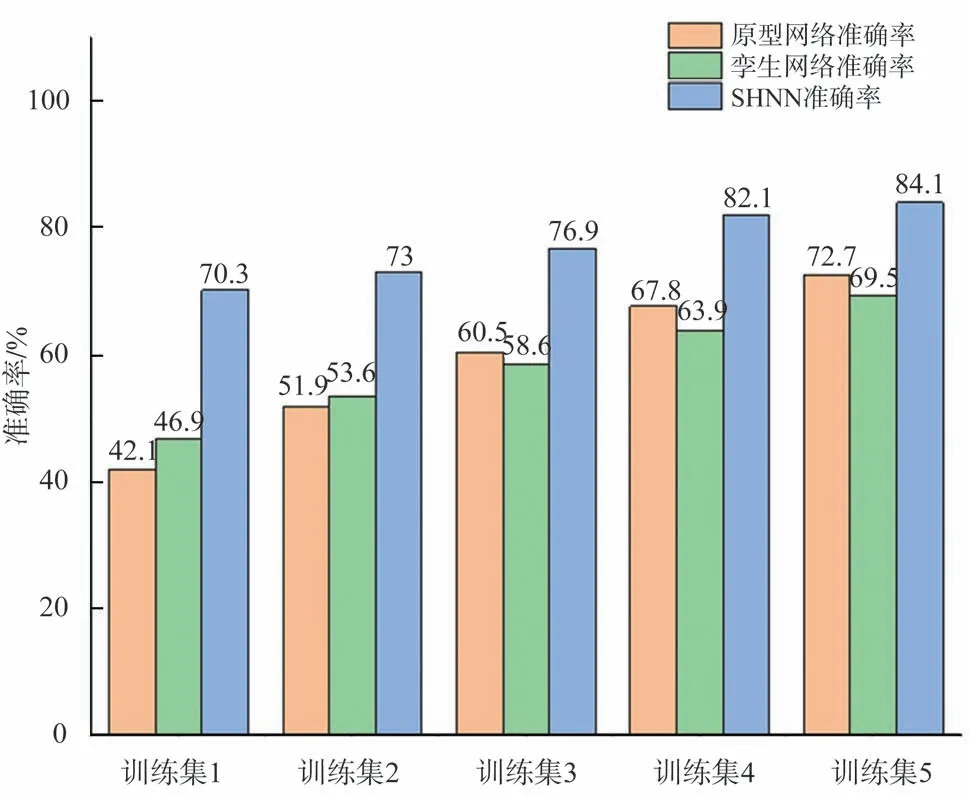
图10 各类故障诊断方法在测试集2诊断准确率Fig.10 Diagnostic accuracy of various fault diagnosis methods in test set 2

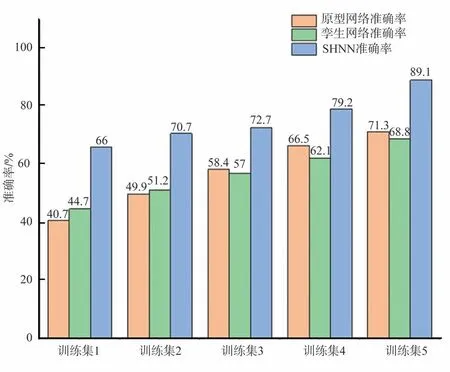
图11 各类故障诊断方法在测试集3诊断准确率Fig.11 Diagnostic accuracy of various fault diagnosis methods in test set 3

综上所述，在变工况的条件下，孪生网络和原型网络模型的诊断准确率逐渐降低，模型的泛化能力较弱。本文提出的SHNN 算法在变工况条件下训练测试不同规格的小样本数据集，仍得到较佳的故障诊断性能。因此，相较于其他方法，SHNN诊断模型表现出了优异的泛化能力。

3 结论

本文对多工况小样本数据集的四旋翼飞行器故障诊断方法进行了深入研究，提出了一种基于CNLS-MMD 的孪生混合网络四旋翼飞行器故障诊断方法，采用将CNN对空间特征的提取能力与LSTM对时域数据信号特征的提取能力相结合的特征提取网络来改进诊断模型的特征提取网络，利用MMD 优化网络相似度的度量方法，构建了SHNN故障诊断模型，实现了对四旋翼飞行器的故障诊断。利用实验室采集的四旋翼飞行器飞行数据进行了相关试验，结果表明，与原型网络和孪生网络两种方法相比，本文提出的基于CNLS-MMD的孪生混合网络四旋翼飞行器故障诊断方法在多种小样本条件下均具有更高的故障诊断准确率，同时在小样本与变工况条件叠加的场景下，表现出了较佳的故障诊断性能和优秀的泛化能力。