基于声扰动方程的气动噪声传播积分计算方法

郑雯斯，王芳

1.西北工业大学，陕西 西安 710072

2.北方民族大学，宁夏 银川 750030

以FW-H 方程[1]为代表的经典声比拟理论假设介质整场均匀，建立了声压与不同类型声源之间的响应关系，成为工程应用中最受欢迎的气动噪声预测方法[2]。但流动在声源区域通常存在梯度，对近场声传播起决定性作用的是声源相对于紧临周围（约一个波长左右范围）的非均匀平均流运动，而不是相对于无穷远处的均匀介质运动。为了将非均匀平均流的作用包括在声比拟理论中，需建立一个恰当的波动方程来描述声波产生与辐射过程。

文献[3]～[6]对非均匀平均流中的声传播进行了研究，提出了各自的波动方程。Goldstein[7]提出广义声比拟理论，将N-S方程重组为对流形式的线化N-S方程组，以此分析了射流中“真实”的气动声源。这些对流波动方程深化了人们对气动噪声产生机理的认识，但面对复杂流动问题，用于求解这些方程的格林函数不能获得理论解。在实际应用中，如何准确求解格林函数成为噪声预测中的一个关键。Tam[8]考虑了非均匀平均流的声折射作用，发展了关联近场声源和远场声压的伴随格林函数方法，计算量小且不存在积分奇点，目前仅应用于固体边界不起主要作用的气动噪声问题，如Karabasov 等[9-10]采用伴随格林函数对射流噪声在非均匀介质中的传播进行过研究。针对非均匀介质中声传播，Goldstein[11]提出了线化势函数模型，Pierce[12]发展了高频近似模型，Bras 等[13]则应用两个模型分析了运动介质中声传播的直接问题和伴随问题。伴随方法有益于解决非均匀介质中声传播问题，Spieser 等[14]采用伴随方法研究了Ma0.9 的湍流噪声问题，赵雯[15]采用伴随方法分析了矩形喷口射流噪声。

流动发声与涡之间存在密切联系，Powell[16]和Howe[17]提出的涡声理论能从物理上清晰地解释流体运动诱发气动噪声的机理，认为涡是流动发声的根本原因。目前，涡声理论多应用于低马赫数流动产生的气动噪声问题，并认为声波是在均匀介质中传播，忽略了平均流与声波间的相互作用。Ewert等[18]提出了考虑介质非均匀效应的声扰动方程，但需要利用高精度时空离散格式[19-20]和无反射边界条件[21-22]在时域内计算声传播，因而效率低。

高效、准确预测声传播是气动声学研究的一个重要方向。为了将涡声思想应用于非低马赫数流动，本文采用声扰动方程描述声波运动，依据伴随方法构建关联近场声源与远场声压的频域格林函数，从而发展一种高效、准确的声传播积分方法，可为复杂流动气动噪声产生机理和复杂介质气动噪声传播机制分析提供理论与方法支持。

1 方法描述

1.1 声扰动方程

忽略黏性和热传导对声传播的影响，N-S方程可简写为

式中，标量ρ，p及矢量u，分别表示当地瞬态流动的密度、压力和速度。将当地流动分解为平均流和非稳态扰动两部分，即

式中，ρˉ，pˉ和uˉ表示无穷远均匀来流分量；ρ′，p′和u′表示非稳态扰动量。利用式（2）线化式（1），得到

1.2 伴随格林函数法

对图1（a）所示声波直接辐射问题，观察点和声源位置分别用矢量x和y表示，关联两者的格林函数为G(x,y)。为获取满足式（6）的格林函数，需将图1（a）所示的直接问题转化为图1（b）所示的伴随问题，伴随格林函数用G(y,x)表示。对线性声学问题，根据声学互易定理有G(x,y) =G(y,x)。用G4和Gi（二维问题i=1, 2，三维问题i=1, 2, 3）分别表示压力型和速度型伴随格林函数。根据式（6），G4和Gi在频域内满足

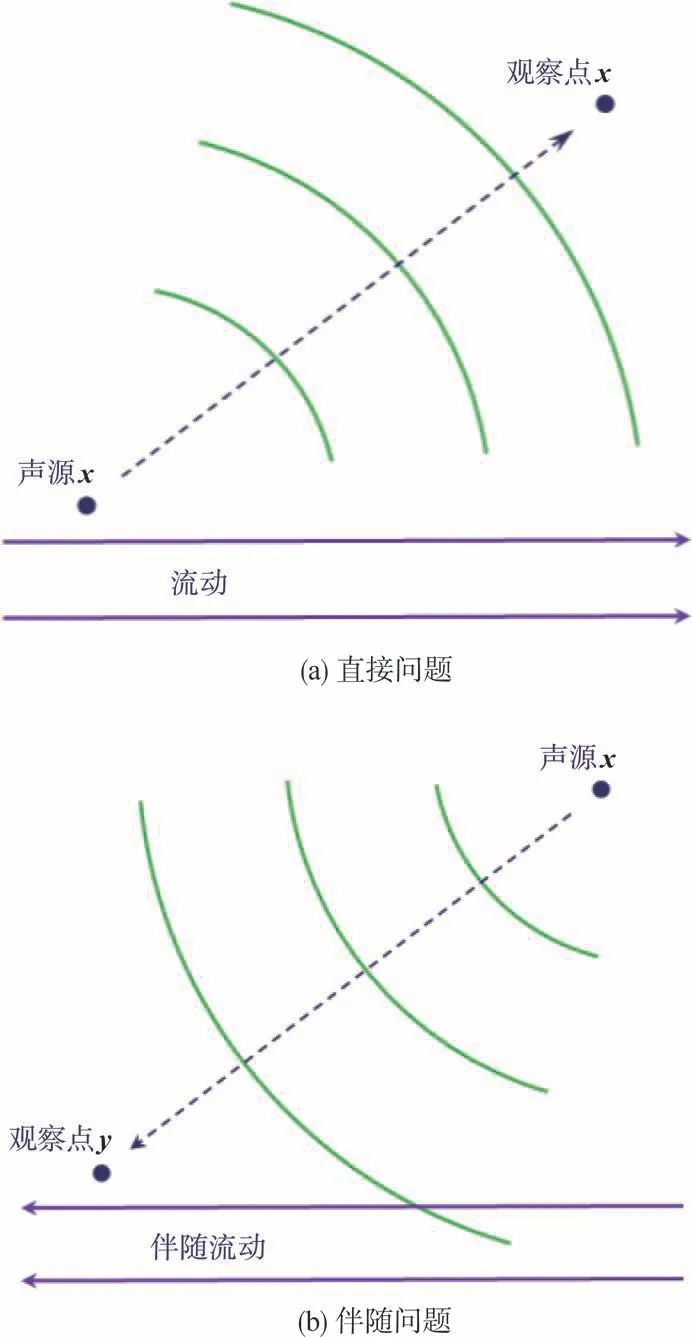
图1 直接问题与伴随问题示意图Fig.1 Schematic of direct and adjoint problems

式中，i和ω分别为虚数单位和圆频率。

采用有限差分方法求解式（8）以获得压力型和速度型伴随格林函数的数值解。空间离散采用五点四阶中心差分格式。将声传播区域分为常系数和变系数波动区域两部分，在常系数区域使用缓冲区（Buffer Zone）边界条件结合拉伸网格的方法来吸收和衰减声波，在固体边界施加声学硬边界条件。

远场声传播可采用下述积分方程描述

2 算例验证

利用二维圆柱和NACA0012翼型绕流算例来验证上述气动噪声预测方法的可靠性。采用Fluent软件计算非定常流动以提取气动声源，湍流模型选择基于S—A模型的IDDES方法。

2.1 二维圆柱气动噪声预测

二维圆柱直径D=0.04m，无穷远均匀来流马赫数为0.3，基于直径的雷诺数Re为100。流动远场距离圆柱中心200D，对圆柱尾涡脱落区域进行网格加密处理，结构化网格总数约为20 万个，声学积分区域位于红色线条内部，如图2所示。

图2 二维圆柱网格Fig.2 Configuration of mesh gird of 2D cylinder

图3 为二维圆柱绕流展向涡量的空间分布云图，低雷诺数层流运动在圆柱尾迹区域出现了周期性的涡脱落。流动计算得到的尾涡脱落频率为416Hz，相应的无量纲频率St=0.161。

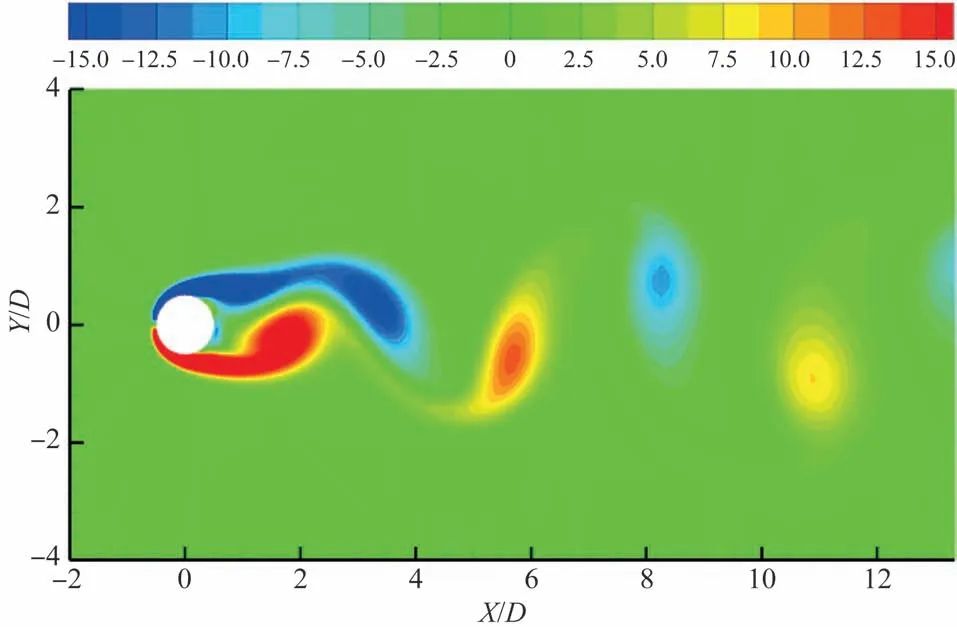
图3 二维圆柱瞬时展向涡量云图Fig.3 Snapshots of the instantaneous spanwise-vorticity structure of 2D cylinder

将声学观察点置于以圆柱中心为原点、半径为20D的圆上。对圆柱尾涡脱落频率噪声，选取120°观察点，非均匀平均流和均匀平均流条件下压力型伴随格林函数虚部的空间分布如图4 所示，两者结果几乎一致。尾涡脱落频率波长与圆柱直径比约为20，意味着近场非均匀流动区域的特征尺寸远小于一个波长，这使得近场流动非均匀性对声传播的影响可以忽略不计。

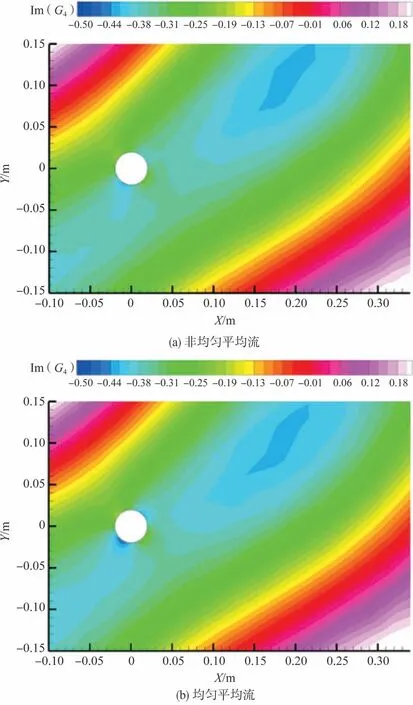
图4 二维圆柱压力型伴随格林函数虚部云图Fig.4 Snapshots of the imaginary part of the pressure pattern adjoint Green's function for 2D cylinder

数值预测的90°观察点声场频谱如图5所示，与计算流体力学（CFD）直接计算结果相比，尾涡脱落频率St=0.161及其一阶谐波St=0.322 处，两者的噪声大小具有很好的一致性。图6进一步显示了尾涡脱落频率的声压级指向性分布，各观察点处的数值预测结果与CFD直接计算值非常吻合，最大误差约为1dB。

图5 二维圆柱声场的声压级频谱Fig.5 Spectrum of sound pressure level of 2D cylinder

图6 二维圆柱尾涡脱落频率声场空间指向性分布Fig.6 Directivity of sound pressure level at the frequency of vortex shedding of 2D cylinder

2.2 二维NACA0012翼型气动噪声预测

NACA0012翼型弦长C=0.1m、迎角为7°的均匀来流马赫数Ma=0.4，基于弦长的雷诺数Re=5×104。流动远场距离翼型中心200C，网格总数约为32 万个，在流动分离区域进行网格加密处理。图7 为瞬时展向涡量空间分布，流动计算所得尾涡脱落频率为St=2.92，对应的声波波长与翼型弦长比为0.85，波长接近弦长预示非均匀平均流对声波传播的影响不能忽略。

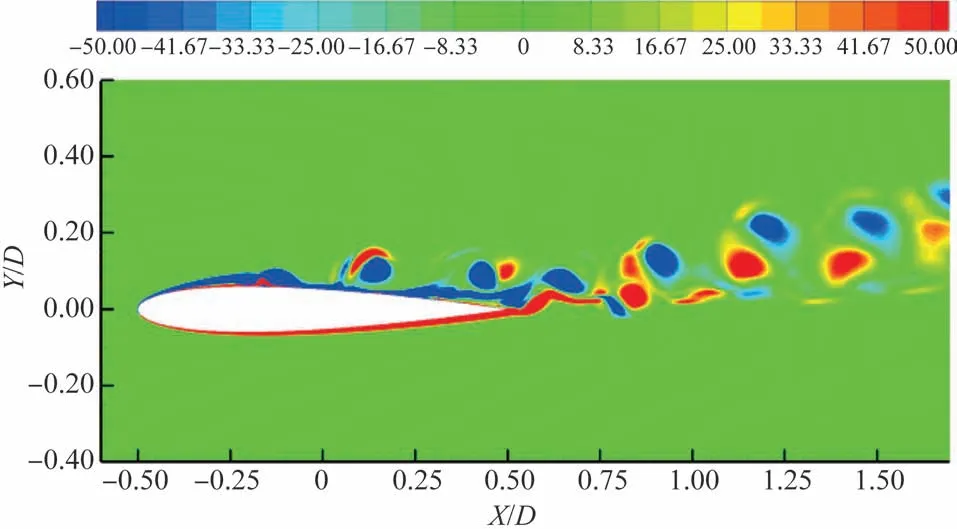
图7 二维NACA0012翼型瞬时展向涡量云图Fig.7 Snapshots of the instantaneous spanwise-vorticity structure of 2D NACA0012 airfoil

观察点布置在以翼型流向中心为原点、半径为10C的圆上。对涡脱落频率St=2.92，选取60°观察点，非均匀平均流和均匀平均流条件下压力型伴随格林函数幅值的空间分布如图8 所示。两者的空间分布基本相似，但在涡脱落区域存在明显差异。

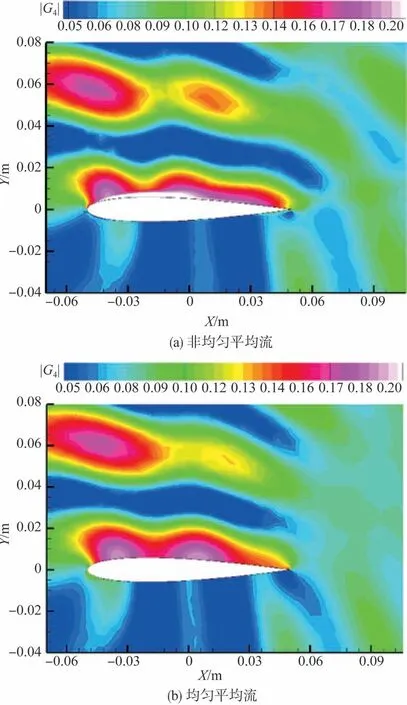
图8 二维NACA0012翼型压力型伴随格林函数云图Fig.8 Snapshots of the pressure pattern adjoint Green's function for 2D NACA0012 airfoil

图9 进一步给出了非均匀平均流和均匀平均流条件下，60°观察点对应的速度型伴随格林函数G1实部的空间分布。类似压力型伴随格林函数，涡脱落区域的非均匀平均流对声传播存在显著影响。

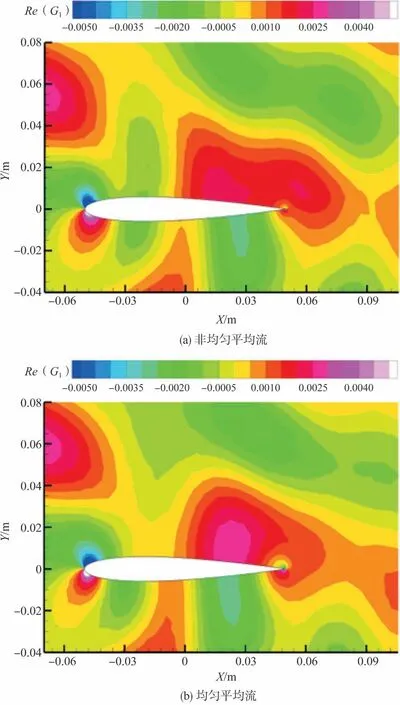
图9 二维NACA0012翼型速度型伴随格林函数实部云图Fig.9 Snapshots of the real part of thevelocity pattern adjoint Green's function for 2D NACA0012 airfoil

图10 给出了90°观察点声场频谱数值预测结果，与CFD 直接计算结果对比，两者在频率分布和峰值大小上基本一致。三个主要峰值频率（St=1.96, 2.92, 3.87）的噪声结果对比见表1，可以看出，St=2.92 处的噪声差异最大，声压级的数值预测结果比CFD直接计算值高1.3dB。图11进一步展示了不同频率下的声压级指向性分布，在各观察点处，本文方法的数值预测结果与CFD直接计算值吻合较好。

表1 二维NACA0012翼型主要峰值噪声Table 1 Main peak noise of 2D NACA0012 airfoil

图10 二维NACA0012翼型声场频谱Fig.10 Spectrum of sound field of 2D NACA0012 airfoil

图11 二维NACA0012翼型不同频率声场指向性分布图Fig.11 Directivity patterns of 2D NACA0012 airfoil noise at different frequencies

3 结论

为了考虑非均匀介质声折射对气动噪声传播的影响，本文采用声扰动方程描述声波在非均匀介质中的传播，基于声学互易原理构建关联近场声源与远场声压的频域伴随格林函数。进而利用伴随格林函数和声扰动方程源项的数值计算结果，通过频域积分计算噪声传播。通过研究可以得到以下结论：

（1） 二维圆柱和NACA0012翼型绕流噪声的频谱和指向性预测结果与CFD直接计算值吻合。

（2） 对声波波长远大于非均匀流动区域范围的声辐射问题，可以直接忽略非均匀流动对声传播的影响；而当声波波长与非均匀流动区域特征尺寸相近时，非均匀流动对声波的折射作用明显。