基于滑模观测器的飞翼无人机输出反馈控制

顾子箫，赵振华，闻子侠，曹东

1.南京航空航天大学，江苏 南京 211106

2.航空工业西安飞行自动控制研究所，陕西 西安 710061

飞翼布局无人机具有升阻比大、气动效率高、隐身性能好等诸多优点，近年来在民用和军事领域都得到了广泛的应用[1-2]。飞翼无人机构型具有翼身高度融合、无垂尾等特点，造成其在机动飞行过程中的纵、横向通道间耦合比常规布局飞机更加严重[3]。随着飞行环境日益复杂，飞翼无人机不可避免地受到外部风干扰、内部参数摄动和未建模动态等多源干扰的影响[4]。飞翼无人机的通道解耦和多源干扰环境下的干扰抑制成为飞翼无人机控制系统设计的关键。

针对飞翼无人机的控制设计问题，研究人员提出了许多有效的方法。针对飞翼无人机非线性系统，李继广等[5]采用反步法对复杂轨迹进行跟踪，在没有外界干扰作用下获得了良好的跟踪性能。冯引安等[6]提出了基于H∞的鲁棒反步姿态控制方法，该方法与传统反步控制相比设计更为简单，且提升了飞翼无人机控制系统的鲁棒性。李继广等[7]通过对非线性模型进行线性化解耦， 保证了航迹跟踪误差的渐近收敛。

基于干扰观测器的控制（DOBC）方法将干扰和不确定性的综合影响视作集总干扰，并使用观测器技术来估计集总干扰，然后基于干扰估计值设计控制器实现干扰的前馈补偿[8]。DOBC方法能够对干扰进行直接补偿，获得了更快的干扰抑制性能[9]，在工业控制系统中得到了广泛的应用[10-11]。针对受多源干扰影响下的四旋翼无人机系统轨迹跟踪控制问题，赵振华等[10]提出了一种基于扩张状态观测器的复合滑模控制器方案，将无人机各个通道的耦合和多源干扰视为集总干扰，并设计扩张状态观测器对其进行估计，显著提升了受扰四旋翼无人机系统的轨迹跟踪精度。张波等[11]针对强干扰环境下飞翼无人机的姿态控制问题，基于扩张状态观测器设计了一种复合指令跟踪控制器，能够保证无人机的姿态跟踪误差收敛有界，实现了姿态指令的高精度跟踪。

本文研究了受多源干扰影响的飞翼无人机高度和速度跟踪控制问题，提出了一种基于高阶滑模观测器的复合输出反馈主动抗干扰控制方法。首先，将飞翼无人机的高度和速度指令跟踪控制问题转化为跟踪误差镇定问题。其次，将高度和速度通道间的耦合和多源干扰影响视为集总干扰，得到高度和速度的跟踪误差动态，并设计高阶滑模观测器（HSMO）估计跟踪误差的动态和集总干扰信息。最后，基于HSMO的估计设计复合非线性动态逆输出反馈控制器。

1 系统建模与问题提炼

1.1 飞翼无人机纵向动态

受干扰影响的飞翼无人机纵向动力学模型可为

式中，H为高度；V为速度；α和γ分别为迎角和航迹角；q为俯仰角速率；m为质量；Iyy为转动惯量；g为重力加速度；dv,dγ,dq为干扰；L,D,T,M分别为升力、阻力、发动机推力、俯仰力矩，分别表示为

式中，ρ为大气密度；S为飞翼无人机的参考面积；c为机翼平均气动弦长；Kp为发动机常数；CL,CD,CM为升力、阻力、俯仰力矩的气动力系数，且可以计算为如下形式[12]

式中，δe为升降舵偏转角度。为便于设计控制器，采用二阶系统来表征飞翼无人机发动机的动态[13]

δ̈T=- 2ξωnδ̇T-ω2nδT+ω2nδt（2）

式中，δT和δt分别为真实的发动机实际油门开度和发动机油门开度指令；ξ和ωn为反映发动机特性的已知常数。

1.2 问题提炼

考虑到飞行高度和速度对无人机飞行的重要性，本文主要研究飞行高度和速度的跟踪问题。定义高度和速度的跟踪误差为

式中，Hd和Vd为高度和速度指令。联立式（1）～式（3），可得无人机纵向跟踪误差动态

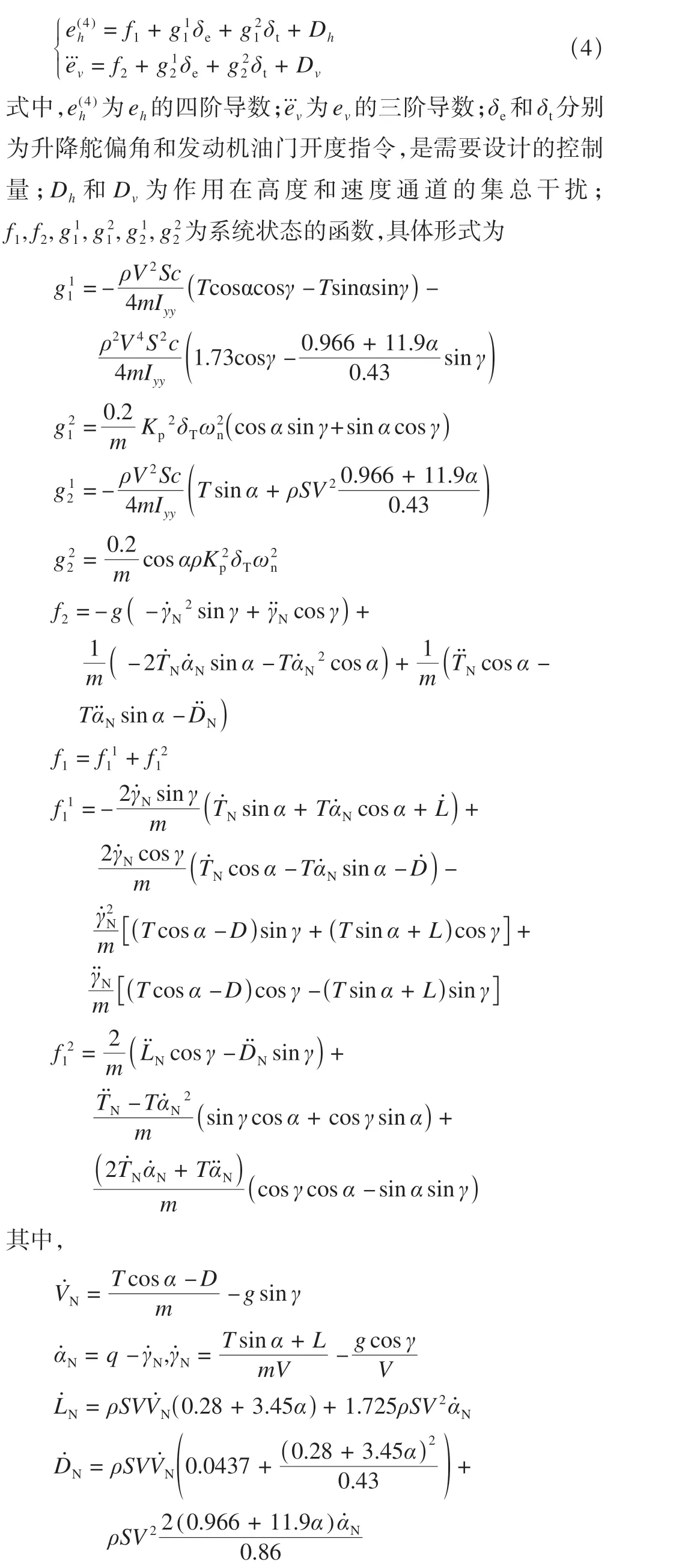
2 控制器设计

本节设计HSMO来估计高度和速度通道跟踪误差的动态以及集总干扰信息。然后基于估计信息，设计复合非线性动态逆（CNDI）输出反馈控制器。

2.1 高阶滑模观测器设计

假设1

式中，loh和lov为HSMO 增益，其取值满足loh≥ldh，lov≥ldv；ė̂h,ë̂h,e…̂h,ė̂v,ë̂v为高度和速度跟踪误差变化率的估计信息；D̂h和D̂v为高度和速度通道受到集总干扰的估计信息。定义HSMO的估计误差为

根据参考文献[14]中的定理可知，观测器误差eėh,eëh,ee…h,eėv,eëv和eDh,eDv能够在有限时间内收敛到零。即高度和速度跟踪误差变化率估计值和集总干扰估计值能够在有限时间内到达其真实值。

2.2 复合非线性动态逆输出反馈控制器设计

定理1

3 稳定性分析

从式（4）、式（8）和式（9）可以看出，高度和速度通道具有明显的对称性，因此后续以高度通道为例对定理1 进行分析，具体证明过程可以分为以下两个步骤。

（1）ėh,ëh,e…h和Dh被精确估计后，高度跟踪误差eh渐近收敛

考虑到式（7），将式（8）、式（9）代入式（4）可得

（2）ėh,ëh,e…h和Dh被精确估计前，状态有限时间内不逃逸

在ėh,ëh,e…h和Dh被精确估计前，高度跟踪误差eh按照式（10）进行变化，考虑到式（10）右侧变量eėh,eëh,ee…h和eDh是式（5）的观测误差，因此eėh,eëh,ee…h和eDh是有界的。由于式（11）是渐近稳定的，将式（10）右侧关于eėh,eëh,ee…h和eDh的函数看作式（10）的输入，根据参考文献[15]中的有界输入有界输出定理可以得到式（10）的状态eh,ėh,ëh,e…h是有界的。因此，无论eėh,eëh,ee…h和eDh是否被准确估计，高度跟踪误差eh及其变化率都是有界的，所以在ėh,ëh,e…h和Dh被精确估计前，式（10）的状态是有界的。

本文所提出的基于滑模观测器的飞翼无人机复合非线性动态逆输出反馈控制结构如图1所示。

图1 基于滑模观测器的飞翼无人机复合动态逆输出反馈控制结构框图Fig.1 Control structure of the composite dynamic inverse output feedback controller for flying wing UAV

4 仿真研究

4.1 仿真设定

本节基于某飞翼无人机结构数据模型，对所提复合动态逆输出反馈控制器的有效性进行仿真验证。样例无人机的本体参数设定为[16]：Iyy=1.135kg·m2,S=0.55m2,c=0.19m,Kp=80，m=13.5kg。

受到的外部阵风干扰设置为dw= 3sin(t)，此时式（1）中空速真实值变为V=Vn+dw,其中，Vn为速度标称值。为了使仿真更具有挑战性，设计两种执行器故障模式：当t≥15s时，油门杆操纵效能损失20%；当t≥35s时，升降舵操纵效能损失20%。为了验证所提出的基于高阶滑模观测器的复合非线性动态逆（CNDI+HSMO）控制算法的优越性，在仿真中分别测试基于广义比例积分观测器（GPIO）的复合非线性动态逆控制算法（CNDI+GPIO）、基于扩张状态观测器（ESO）的复合非线性动态逆控制算法（CNDI+ESO）两种方案进行对比。本文所提CNDI+HSMO 方案的控制器和观测器分别设计为式（8） 、式（9）、式（5）、式（6）的形式，控制器和观测器的参数设置为

观测器设计为ESO时，以高度通道为例，设计形式为

4.2 仿真结果分析

图2～图11 给出了飞翼无人机在三种控制方法下的响应曲线。图2、图3 给出了飞翼无人机高度和速度跟踪误差响应曲线，从图中可以看出，所提CNDI+HSMO方法的跟踪误差具有最快的收敛速度，并且从图2 和图3 的放大图中可以看出，CNDI+GPIO 相比于CNDI+ESO 方法可以保证系统具有更高的跟踪精度。表1 给出了在本文所提CNDI+HSMO 控制方法以及作为对比方法的CNDI+GPIO 和CNDI+ESO 作用下的高度和速度稳态跟踪精度的具体值。从表1 中可以看出，本文所提控制方法作用下的高度和速度稳态跟踪误差分别只有0.02m 和0.01m/s，显著低于CNDI+GPIO和CNDI+ESO方法下的稳态跟踪误差。

表1 不同控制方法稳态跟踪误差Table 1 Steady-state tracking error under different control methods

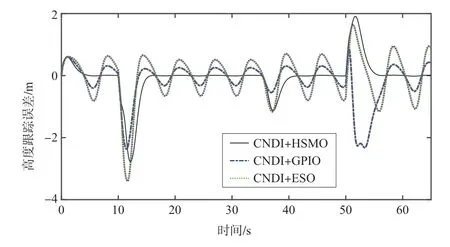
图2 高度跟踪误差响应曲线Fig.2 Response of altitude tracking error

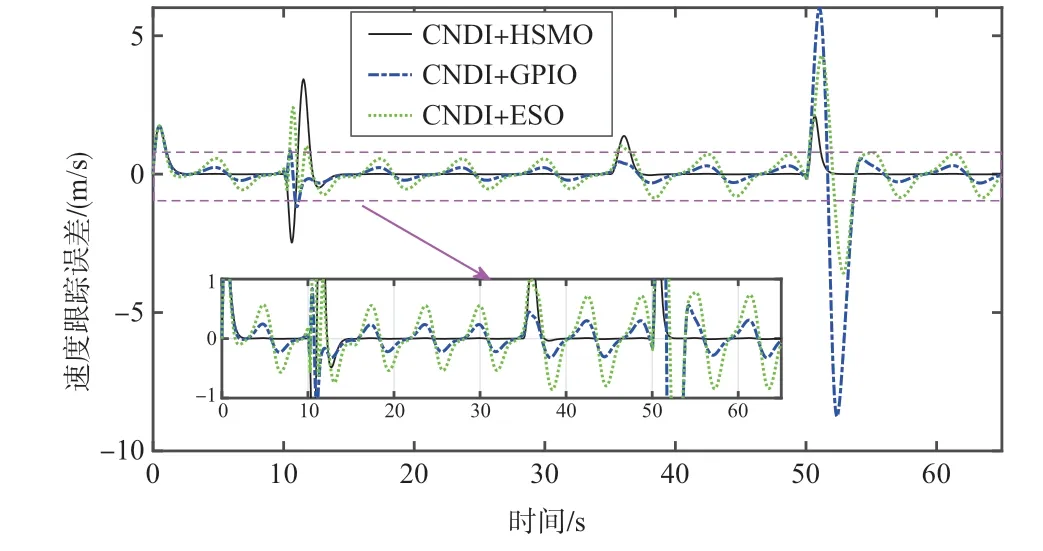
图3 速度跟踪误差响应曲线Fig.3 Response of velocity tracking error

图4～图6 分别给出了不同方法下，飞翼无人机的升降舵偏角、油门开度指令和油门开度响应曲线。从图中可以看出，三种控制方法下的控制量在同一量级，并且三种方法均保证了控制量的连续性。从图5 中可以看出，在10s 和50s 时，无人机油门开度指令随着高度指令的变化而明显发生改变，表明了无人机高度和速度通道的高度耦合特性。

图4 升降舵偏角响应曲线Fig.4 Response of elevator deflection angle

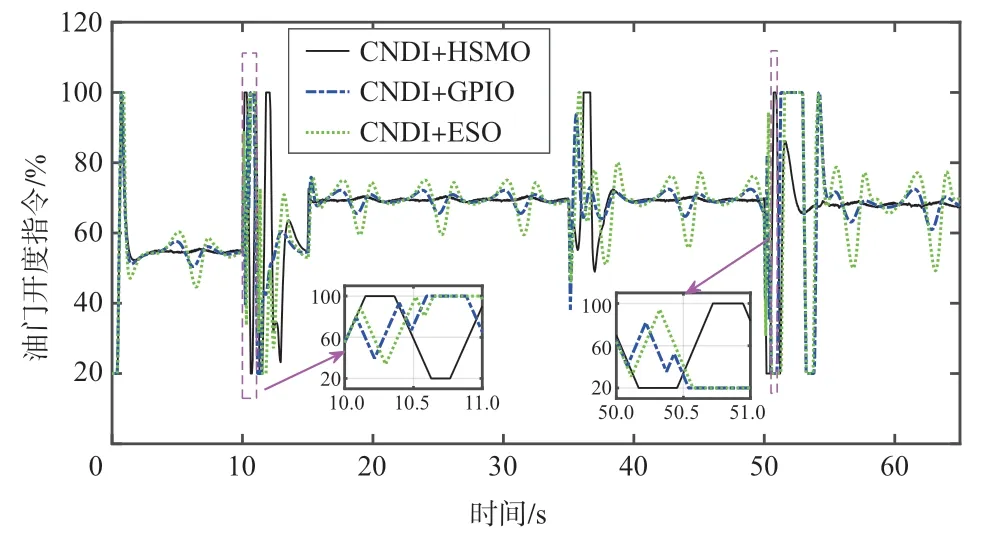
图5 油门开度指令响应曲线Fig.5 Response of engine throttle command

图6 油门开度响应曲线Fig.6 Response of engine throttle

图7～图11 给出了三种不同观测器对高度和速度跟踪误差动态的估计效果。从图7～图11 中可以看出，本文采用的HSMO 方法估计误差的稳态值远小于另两种观测器方法。表2 给出了本文采用的HSMO 观测器以及作为对比的 GPIO 和ESO 观测器对高度跟踪误差动态ėh、ëh和速度跟踪误差动态ėv、ëv的估计精度。从表2 中可以看出，本文所采用的HSMO 方法可以保证高度跟踪误差动态ėh、ëh和速度跟踪误差动态ėv、ëv的估计误差显著低于GPIO 和ESO 观测器，这表明本文采用的HSMO 观测器获得了最好的估计效果。

表2 不同观测器稳态估计误差Table 2 Steady-state estimation error underdifferent observers

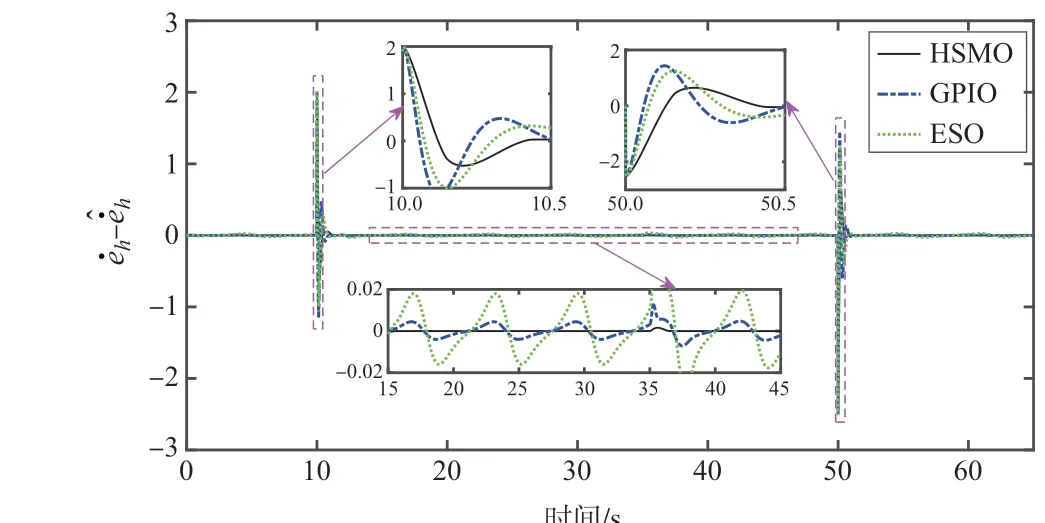
图7 ėh的估计误差曲线Fig.7 Estimation error of ėh

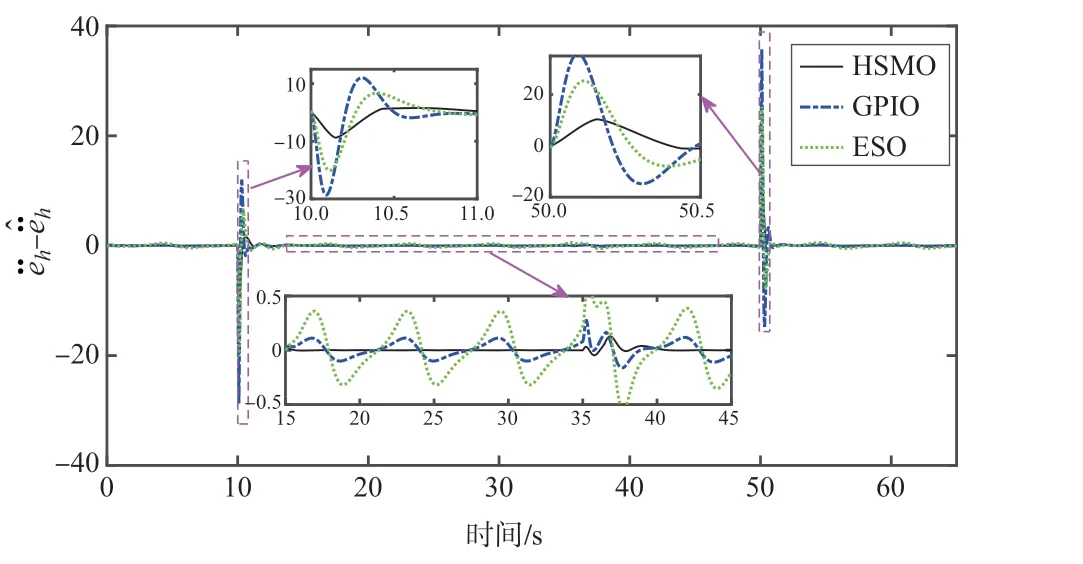
图8 ëh的估计误差曲线Fig.8 Estimation error of ëh

图9 e…h的估计误差曲线Fig.9 Estimation error of e…h

图10 ėv的估计误差曲线Fig.10 Estimation error of ėv

图11 ëv的估计误差曲线Fig.11 Estimation error of ëv

5 结论

本文针对受多源干扰影响的飞翼无人机纵向指令跟踪问题进行研究，提出了一种基于高阶滑模观测器的复合非线性动态逆输出反馈控制方案，仿真结果验证了所提方法的有效性。与已有研究相比，本文的主要创新点有：

（1）通过将耦合项视为干扰，实现了飞翼无人机高度和速度通道之间的解耦，保证了高度和速度通道的独立控制。

（2）实现了跟踪误差高阶动态和时变干扰的高精度估计，保证了复杂干扰环境下指令的高精度跟踪。