航空重力测量重复测线数据处理技术研究
李新宇,周召发,张志利,常振军,郝诗文
火箭军工程大学 兵器发射理论和技术国家重点学科实验室,陕西 西安 710025
以飞机为载体的航空重力测量技术已成为高效测定地球重力场信息的主要手段[1]。在动态重力测量中,测量结果会受到发动机振动、载体动态性、空气扰动等因素的干扰,测量噪声广泛分布,严重影响了重力测量的精度[2]。开展航空重力测量数据处理方法研究,提高数据处理的精度,具有十分重要的意义。
为了抑制噪声对实现重力信息的高精度提取的影响,众多学者对航空重力数据后处理进行了深入研究。频域有限冲激响应(FIR)低通滤波方法在实际中被广泛应用,可以有效消除高频噪声[3]。国外提出了具有特色的滤波方法,如R.R.B.Von Frese 等[4]提出了波数相关滤波器(WCF),通过比较测量数据与协同数据频谱的相关程度来实现噪声分离;B.A.Alberts 等[5]提出了频域加权的方法,对测量数据的不同频段赋予不同的权值,以此来进行降噪处理;Y.V.Bolotin 等[6]在时域处理方法的基础上,将地球重力场的非均匀一致性建模为多状态隐性马尔可夫模型,对结果的细节有所提升。国内方面,罗锋等[7]提出使用Kalman平滑算法开展航空重力测量数据处理方法研究,在国内首次解算出稳定平台式航空重力异常数据,且数据处理精度达到国际先进水平。参考文献[8]将经验模态分解应用到航空重力测量数据处理中,对已经过FIR 低通滤波的航空重力测量数据进行深化处理,可以很好地消除由飞机动态运动引起的动态误差,进一步提高测量精度。针对一直存在的动态效应剩余影响,黄谟涛等[9]基于AIC信息量准则和互相关分析方法提出了一种针对各类动态效应剩余误差的通用补偿模型,内符合精度从原来的9.35mGal提升到1.01mGal。为了削弱各类误差源的影响,欧阳永忠等[10]提出了一种相关分析法和测线网平差两阶段综合误差补偿方法,实测数据处理结果验证了该方法的有效性和可靠性。
通过测线网平差求解系统误差改正量,对各测线重力测量值进行补偿是处理航空重力测量数据的重要方法[11],但现阶段平差方法往往仅适用于规则的测线网[12]。航空重力测量中常常采用重复测线的测量方式来检验航空重力仪动态测量的重复一致性,此时测线网平差的方法便不再适用[13]。蔡劭琨等[14]提出了一种航空重力测量重复测线系统误差自调整的方法,也仅仅可以解决两条重复测线的数据处理,怎样对多条重复测线进行系统平差还需要继续深入研究。
因此,本文提出了基于经验模态分解(EMD)和半系统误差调整的航空重力测量重复测线数据处理方法。首先,推导了航空重力测量的基本原理,并详细分析了测量噪声的来源及误差特性。其次,提出了基于EMD的误差分离方法,对航空重力测量数据的深化处理进一步提高动态重力测量的精度。最重要的是,基于半系统误差调整模型提出了适用于多条重复测线的系统平差方法,填补了该领域的研究空白。最后,通过对实测数据的处理,验证了本文所提数据处理方法的精度和有效性。
1 航空重力测量数学模型
航空重力测量的两个基本问题是如何保持重力敏感器的稳定指向及如何从惯性加速度中分离出重力加速度[15]。平台式重力仪基于跟踪当地地理系的稳定平台,可以隔绝载体角运动的影响,可以有效解决第一个问题。第二个问题的解决依赖于差分GPS,由其可以获取高精度的位置和速度信息,用以计算载体垂向加速度以及重力相关的改正项,进而分离得到重力信息。
1.1 数学原理
式(1)所述的比力方程是动态重力测量和惯性导航系统共同的理论基础

式中,δg为重力异常;f为重力敏感器测量得到的比力;h为载体高度信息,ḧ为载体垂向加速度;γ为正常重力矢量的垂向分量;ωie为地球自转角速度;VE,VN分别为载体相对于地球的东向和北向速度;φ为载体纬度信息;RN,RM分别为地球参考椭球的卯酉圈和子午圈的曲率半径;后三项合记为厄特弗斯改正项δaE。
除厄特弗斯改正项外,航空重力测量还涉及正常重力改正、空间改正、偏心改正、水平加速度改正及垂直加速度改正等多个改正项。
1.2 噪声误差源分析
以飞机为载体的航空动态重力测量数据受到大量具有不同频谱特性且分布广泛的噪声影响,本节依据噪声特性进行分类简述。
1.2.1 高频噪声
在实际航空重力测量中,重力敏感器的输出包含由飞机发动机以及空气湍流造成的随机振动加速度,这部分噪声的强度是重力异常的数万倍,属于高频噪声。因此,需要利用低通滤波的方法进一步去除重力异常信息中的高频噪声。
1.2.2 未知特性噪声
测量条件中各种随机因素产生的偶然误差具有偶然性和随机性,由载体动态性、空气扰动等因素产生的噪声也无法明确其误差特性。基于经验模态分解的数据深化处理是消除这些误差的有效方法。
1.2.3 低频误差
受测量条件中某些特定因素如长周期传感器误差的系统性影响而产生的低频误差被称为系统误差,其与重力信息在同一频段,无法通过低通滤波予以消除。系统误差对观测成果具有累积作用,因此在测量过程中常使用平差方法予以消除。
2 基于EMD的误差分离
构建补偿模型是抑制重力测量动态效应影响的一种方法,但模型构建的科学性及模型参数的准确性严重制约上述方法的有效性。基于数据处理的误差分离是另一种有效的抑制方法。本节提出EMD 对已经低通滤波过后的航空重力测量数据进行深化处理,削弱未知特性噪声对重力测量结果的影响,进一步提高动态重力测量的精度。
2.1 EMD基本原理
EMD 方法认为,任何复杂的时间序列x(t)都可以分解为一组从高频到低频的本征模态函数(IMF)和一个残余信号r(t),这些本征模态函数可以很好地反映信号在任何时间局部的频率特征[16]。分解结果如式(4)所示
每个IMF分量都满足两个条件:一是整个信号上极值点数目与零点数目相差为1;二是极大值与极小值分别构成的包络线均值为0。EMD的分解步骤为:(1)确定原序列x(t)中的极大值和极小值点,并采用三次样条分别对极大值和极小值点进行插值,构造上下包络线xmax(t)和xmin(t),可得上下包络线的均值为m(t);(2)计算原时间序列与包络线均值序列的差值为h(t) =x(t)-m(t);(3)若h(t)满足IMF的两个基本条件,则将h(t)设定为一个IMF分量,并求出剩余分量r(t) =x(t)-h(t),继续执行步骤(4);若不满足,将h(t)替代x(t)返回执行步骤(1)~(3);(4)将r(t)作为新的序列重复执行步骤(1)~(4);循环执行直到提取的最后一个IMF分量或者余项小于预先设定的阈值或已成为单调函数即可结束算法。
2.2 误差分离
基于EMD对航空重力测量数据进行深化处理的误差分离,首先对低通滤波后去除高频噪声的重力数据进行EMD分解,而后根据重力数据与IMF分量的相关性进行筛选并重构得到去噪后的信号。误差分离的流程如图1所示。
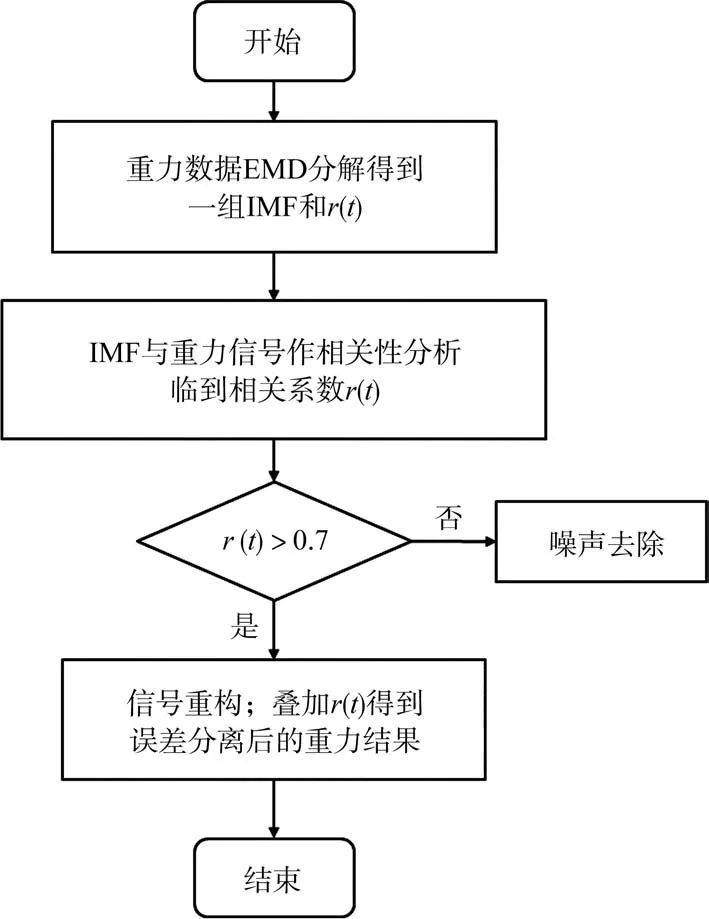
图1 基于EMD的误差分离流程Fig.1 Error separation flowchart based on EMD
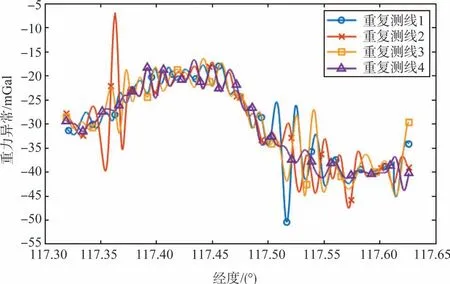
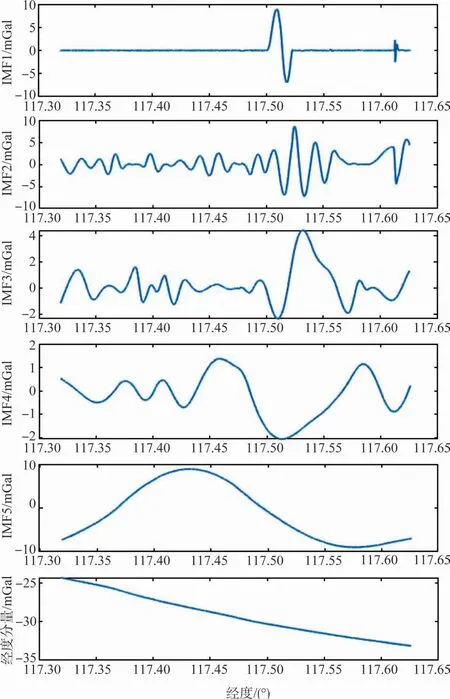
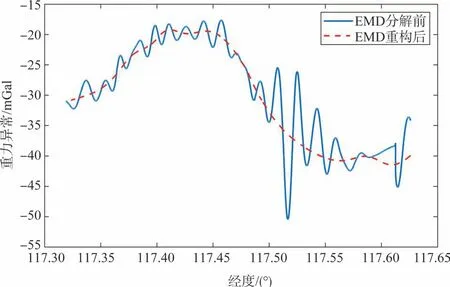
若IMF 分量与重力数据的相关系数r(t)> 0.7,则认定为强相关;若0.2 航空重力测量中各条重复测线在同一测点上的重力异常值理论上应该是相同的,但由于受到系统误差的影响,实际测量值并不相等,存在测点不符值。本节基于测区半系统差调整的算法提出适用于重复测线的平差方法,对测点数据进行补偿,抑制系统误差的影响。 n条重复测线上各选取m个测点进行平差计算,重复测线上重力测量值分别为g1j,g2j,…,gnj,其中j表示某一测点,且j∈[1,m]。将上述测量值用以下模型表示。 式中,g0是j测点上的重力真值;εij和Δij分别表示测线1~n上的系统误差和随机误差。对n条测线上的重力测量值计算均方误差,其中测线i的均方误差计算式为 选取均方误差最小的测线上的测量值为重复测线的重力基准值gˉij。因此可得n条重复测线j测点上的重力不符值为 除去基准测线外的(n-1)条重复测线测点不符值的均值作为该测点的总体不符值,并以该值作为平差的指标,迭代计算至测点总体不符值代数和为0 时结束调整,并按照该方法遍历重复测线上所有测点即可完成重复测线的系统平差处理。 在某次航空重力测量中4条重复测线上获得的重力异常结果如图2所示,所示结果已通过相同的FIR低通滤波器将高频噪声滤除。由图2 可以看出,重力异常数据低通滤波后相对平滑,高频噪声滤除效果较好,但仍然存在明显的振荡和测点不符值,计算得到内符合精度为2.62mGal。 图2 重复测线重力异常结果图Fig.2 Gravity anomaly result map of repeated survey lines 前文已经介绍了EMD分解的原理,下面首先对重复测线1 的重力异常结果进行EMD 分解,得到如图3 所示的分解结果。进行相关性分析后选择相关系数大于0.7 的IMF分量对重力异常信息进行重构,得到EMD去噪前后重力异常结果对比图,如图4 所示,可知EMD 深化处理后重力异常结果中的振荡得到了很好的分离。 图3 reline1重力异常结果EMD分解结果图Fig.3 EMD decomposition result diagram of reline1 gravity anomaly results 图4 reline1重力异常数据深化处理前后对比Fig.4 Comparison between reline1 gravity anomaly data before and after deepening processing 使用同样的方法对其他测线进行EMD分解并重构,得到EMD深化处理后的重复测线重力异常测量结果,如图5所示。重复测线数据EMD处理后消除了原有明显的振荡,计算可得内符合精度为0.75mGal,但测点不符值依然存在,有待进一步平差处理。 图5 EMD去噪后的重复测线重力异常结果图Fig.5 Gravity anomaly results of repeated survey lines after EMD denoising 在重复测线上等间隔选取756 个测点,按照前文设计的重复测线平差算法进行系统误差调整。本文设计的系统平差算法精度与平差次数呈正相关,两者的相关关系如图6所示。由图6 可知,迭代计算至第16 次后测点不符值精度已收敛,756 个测点不符值代数和以及标准差基本为0,此时认为平差结束。 图6 平差算法精度与平差次数关系图Fig.6 Relationship between adjustment algorithm accuracy and adjustment times 平差结束后的重复测线重力异常结果如图7 所示,相较平差前的结果,单个测点的不符值仍然存在,似乎表示该算法的优化作用不是特别明显,但通过计算可知,此时重复测线的内符合精度提升至0.28mGal,相较平差前的0.75mGal已有大幅提升。这是因为本文所提的重复测线平差方法是针对总体测线而言的,因此重复测线总体的内符合精度提升较为明显。 图7 平差后重复测线重力异常结果图Fig.7 Gravity anomaly results of repeated survey lines after adjustment 图8给出了平差前后测点不符值的分布情况。显而易见,平差结束后测点不符值误差明显减小,系统误差得到有效补偿。且测点不符值分布大致满足标准正态分布,说明了各测点之间相互独立。 图8 平差前后测点不符值分布图Fig.8 Distribution map of inconsistent values of measurement points before and after adjustment 基于EMD分解有效分离了信号与误差,本文提出的重复测线平差方法在总体上对系统误差进行调整,进一步提高了总体测线的内符合精度。重复测线内符合精度统计见表1,由此可知本文的研究内容显著提升了数据处理的精度。 表1 重复测线内符合精度统计Table 1 Statistical table of inner coincidence accuracy ofrepeated lines 本文针对航空动态重力测量噪声分布广泛的问题,对重复测线的误差分离展开研究,提出了基于EMD和半系统误差调整的航空重力测量重复测线数据处理方法。实测数据的处理结果表明,EMD 的深化处理将内符合精度从2.62mGal 提升至0.75mGal,有效分离出噪声的影响;经平差处理后抑制系统误差的影响,内符合精度进一步提升至0.28mGal,精度依次提升了71.37%和62.67%。本文研究内容对进一步推动航空动态重力测量精度提升和工程应用化具有积极意义。3 重复测线系统误差调整

4 实测数据分析
4.1 EMD分解
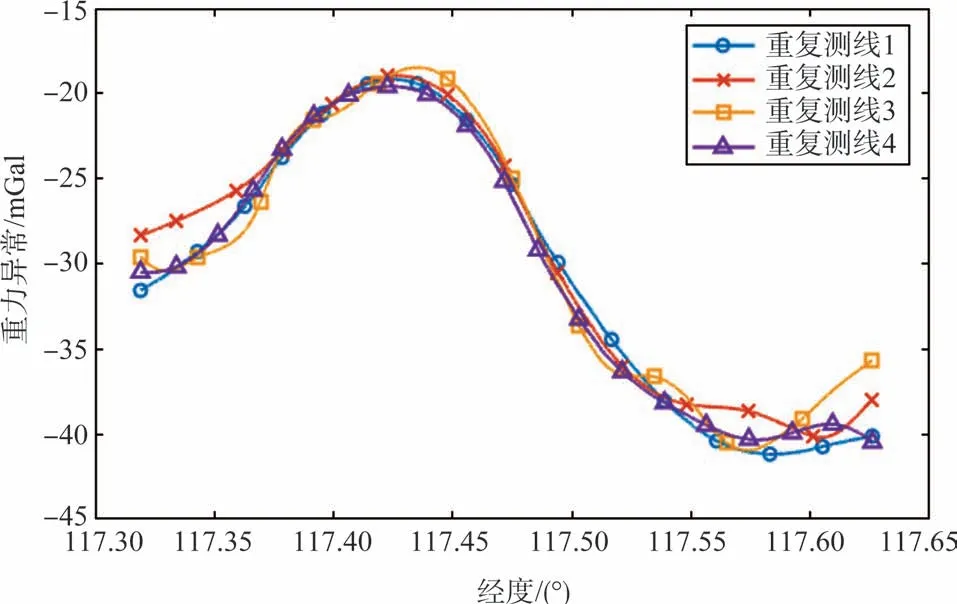
4.2 重复测线平差调整
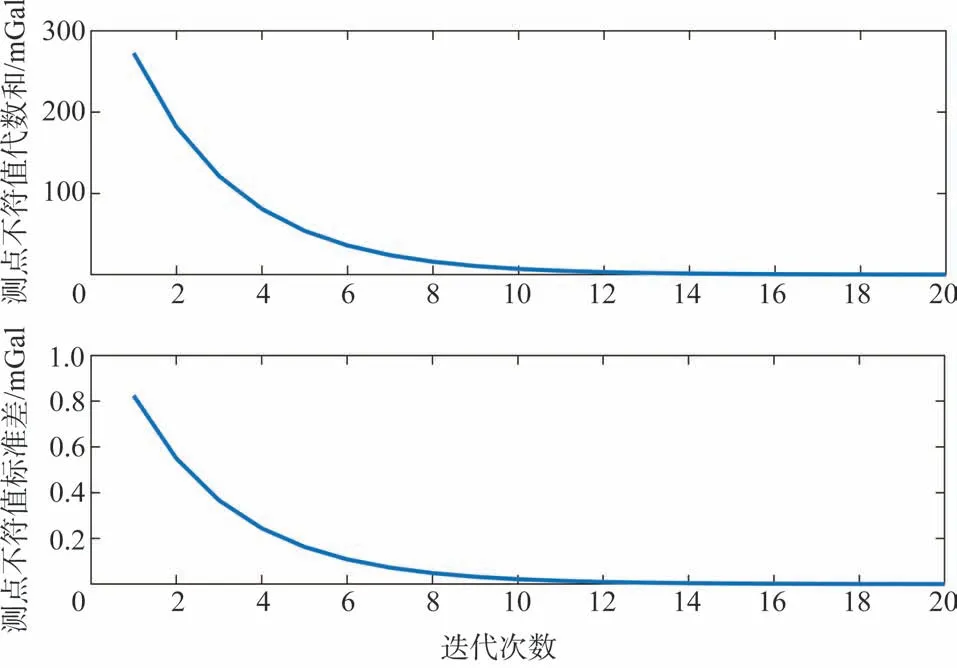
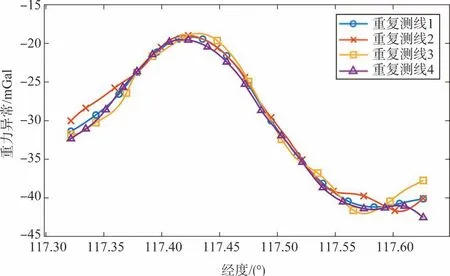
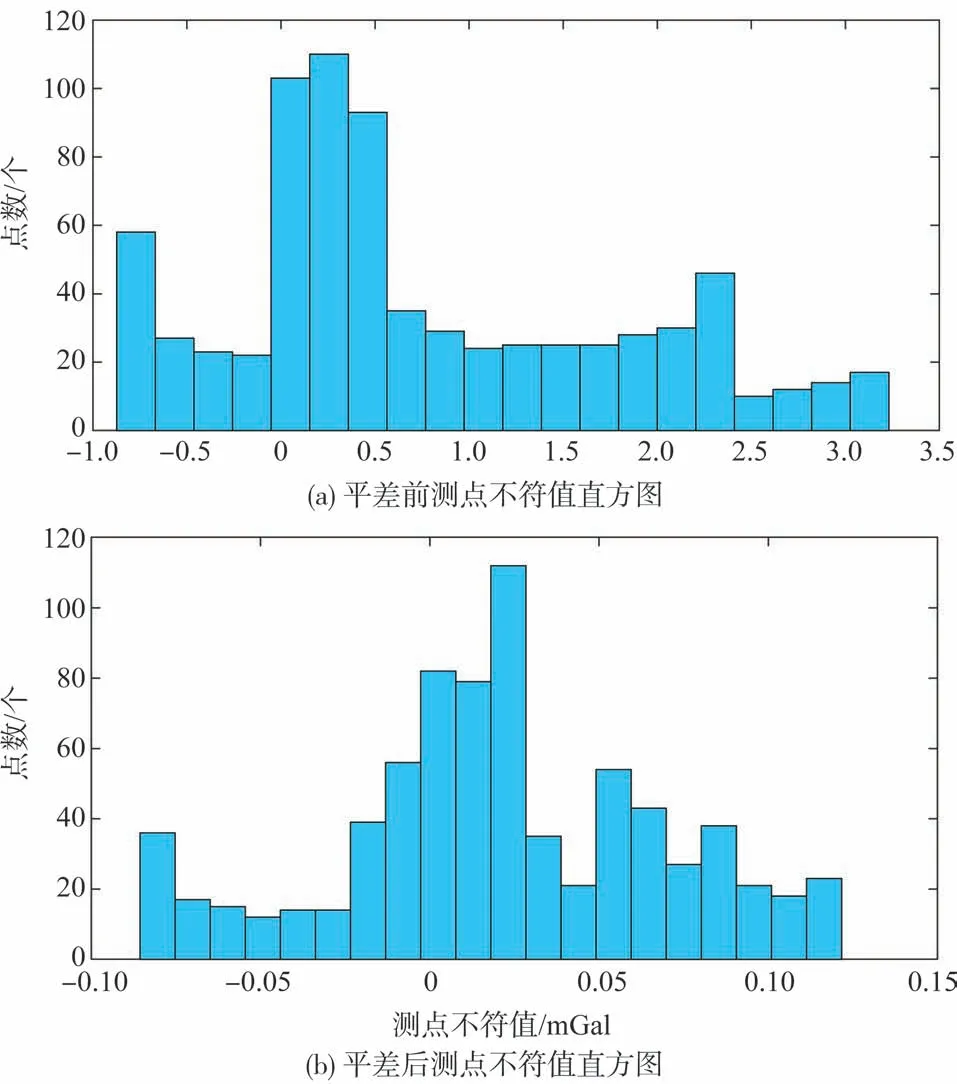
4.3 结果分析

5 结论

