计算第一型曲面积分的截曲线法
罗志刚
(湖北工业大学 理学院, 武汉 430068)
0 引 言
文献[1]通过考虑用曲面族去截积分区域,推广了计算三重积分的截面法,并且指出这个方法对一般的n≥2重积分都适用.特别地,二重积分的情形,结果为
(1)
其中Cξ=D∩{(x,y)|ξ=φ(x,y),α≤ξ≤β}是覆盖了积分区域D的截曲线族, dsξ是Cξ上的弧长元.然而,放到三维空间来看,二重积分不过是第一型曲面积分当被积曲面位于xOy平面内时的特殊情形.这提示笔者去考虑:定义在三维空间中一般曲面上的第一型曲面积分,是否也有类似于(1)的公式?
具体说来,如果被积曲面S与曲面族Sξ的交线Cξ=S∩Sξ当参数ξ跑遍区间[α,β]时覆盖了曲面S,那么可以先完成截曲线Cξ上的(第一型曲线)积分,然后将诸截曲线的贡献积分起来,结果有望等于S上的第一型曲面积分:
其中的被积式(…)待定.
本文给出的定理表明上述考虑完全正确,并且相关结果还可以推广到n维(n≥2)空间.这些定理的证明使用了文献[1-2]中的微分形式计算技巧.关于外微分和微分形式的初步介绍,可以参看文献[3].文献[1]以及本文的结果都可以看作Fubini定理的推广.
为了避免讨论积分的存在性问题,本文中出现的函数,都假定在所论及的定义域上具有一阶连续偏导数.
1 主要结果
定理1曲面S={(x,y,z)|F(x,y,z)=0}与曲面族Sξ={(x,y,z)|ξ=φ(x,y,z),α≤ξ≤β}的交线为曲线族Cξ=S∩Sξ,若S被Cξ覆盖,则有
(2)

证将F(x,y,z)=0与ξ=φ(x,y)分别微分,有
Fxdx+Fydy+Fzdz=0,φxdx+φydy+φzdz=dξ,
(3)
任何一点附近,以下三个行列式
不能都为零.不妨设Dx≠0,这意味着dy和dz可以从(3)式中解出(或者说曲面S局部地可以用(ξ,x)参数化):
(4)
所以
S上的面积元[1]
其中dξdx=|dξ∧dx|.由此,原第一型曲面积分化成累次积分
(5)
在Cξ上作积分时,ξ暂时固定.
另一方面,曲线Cξ上dξ=0,由(4)得到
(6)
注意,这里的dx,dy,dz都被约束在Cξ上.弧长元
因此,(5)中Cξ上的积分可写作
(7)
由(6)知,在Cξ上
所以
(8)
其中应用了Fxdx+Fydy+Fzdz=0.将上式代入到(7)中,即证明定理.
上述证明方法不用作实质性的修改,就可以用来得到n维(n≥3)空间的超曲面上的一般定理:
定理2已知n维(n≥3)空间中,
S={(x1,…,xn)|F(x1,…,xn)=0},Sξ={(x1,…,xn)|ξ=φ(x1,…,xn),α≤ξ≤β},Cξ=S∩Sξ.
若超曲面S被超曲面族Cξ所覆盖(注意,Cξ比S低一维),则有
(9)
其中n(n+1)/2个行列式
而
和
分别是S和Cξ上的面积元(dSξ是比dS低一维的面积元).
经过验证,上述定理对n=2同样正确(此时Cξ是点,其上的积分等于被积函数在这些点上取值之和).
值得注意的是,文献[4]也讨论了这里的问题,但只考虑了用平行平面族去截被积曲面这种特殊情况,我们这里是最一般的结果.
2 应 用
下面举例子来说明上述定理的用法.其中,第一个例子取自文献[4].

解此问题的常规解法是化二重积分.曲面S可以分成两片
从而有
其中D={(z,x)|-1≤x≤1,0≤z≤2+x}.化累次积分,可得
最后一步对x的积分稍稍复杂.
下面用本文的定理求解.为便于对比,用两种不同的方法选取截曲面族.
法1取
F(x,y,z)=x2+y2-1,ξ=φ(x,y,z)=y, -1≤ξ≤1,
可以求得
以及
由定理1得
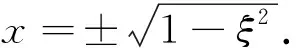
最终得到
法2取
截曲线Cξ=S∩Sξ为椭圆(其中C1和C∞分别是S的边界线).可以得到
应用定理1,有
为了求出Cξ上的积分,将Cξ参数化:
其中0≤θ≤2π.曲线Cξ上的弧长元
所以
从而得到
不言而喻,只有当截曲线Cξ上的积分容易算出时,本文的方法才更具有实用价值.
例2求平面x+y+z=b上被曲面x2+y2+z2-xy-yz-zx=a2截出部分的面积(a>0).
解取
F(x,y,z)=x+y+z-b,ξ=φ(x,y,z)=x2+y2+z2-xy-yz-zx, 0≤ξ≤a2,
容易求出
应用定理1,所求面积为



最后,对参数ξ积分,得到

最后,举一个n维空间的例子来说明(9)的应用.

解超球面Sn(R)的面积为[1]
An(R)=An(1)Rn-1,
因此,要先计算单位超球面Sn(1)的面积An(1).取
则有
行列式Dxixj中,非零的只有
其中i 应用 得出 其中B(x,y)和Γ(x)分别是第一类和第二类Euler积分[5].已知A2(1)=2π,反复运用上述递推式,最后有 与文献[1]一致.但这里的方法直接建立了An(1)与An-1(1)的递推关系,显然更简单. 通常,计算第一型曲面积分总是先将曲面作参数化(坐标面投影也是一种特殊的参数化),然后转化成二重积分来处理.本文的定理给出另一种方案:将被积曲面用一族截曲线覆盖,先在截曲线上完成积分,之后将所有截曲线的贡献积分起来.实际应用中,如果截曲线上的积分很容易作出来,原第一型曲面积分的值往往能立即求得.这为第一型曲面积分的计算提供了更多的可选方案. 致谢感谢相关文献对本文作者的启发以及审稿专家提出的宝贵意见.
3 结 论

