实矩阵次合同的条件
刘可为
(合肥工业大学 数学学院, 合肥 230601)
0 引 言
矩阵合同是线性代数中的一个重要概念,矩阵合同关系的判定是常见的问题之一.对称矩阵合同关系的判定在线性代数教材中已有简单实用的经典结论,但非对称矩阵合同关系的判定则比较困难.近年来,文献[1-4]给出了一些非对称矩阵合同关系的判定方法.
对称矩阵、对角矩阵等特殊矩阵在线性代数的教学与研究中有着重要的作用,二十世纪六十年代我国的一些学者开始提出了矩阵的次转置、次对称、次正交、次正定等概念,并得到一些很好的结果,现已广泛应用于工程技术,统计等领域[5-9].
随着研究的深入,人们发现次正定矩阵在矩阵方程论、经济数学、信息论、线性系统理论等众多学科领域有着重要作用.由于次合同变换不改变矩阵的次对称性,因此矩阵的次正定性判定可通过次合同变换把矩阵化为标准型,再通过标准型次对角线上元素来判定.那么,如何选择合适的次合同变换化矩阵为标准型,如何判定矩阵次合同就有着重要意义.受上述研究的影响,本文考虑实矩阵的次合同,探讨了矩阵的次合同与合同之间的关系,并研究了如何判定矩阵的次合同.
1 n阶方阵的次合同
定义1[5]设m×n阶矩阵A=(aij)m×n,若矩阵B=(bij)n×m满足bij=am-j+1,n-i+1,则称B为A的次转置矩阵,记为B=AST.若A=AST,则称A为次对称矩阵;若A=-AST,则称A为反次对称矩阵.
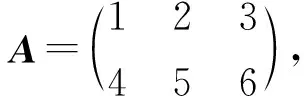

为了后续叙述方便,记AT为矩阵A的转置矩阵,As,Aas,Ass与Aass分别为n阶方阵A的对称, 反对称,次对称与反次对称部分;E为n阶单位矩阵,J为次对角线上元素全为1,其余元素全为0的n阶方阵.矩阵A与B合同,记为A≃B.
为了方便说明本文的主要结果,先给出文献[6-7]中两个结果如下.
引理1[6]设A为m×n阶矩阵,则AT=JnASTJm.
由引理1易得,若A为m×n阶矩阵,则AST=JnATJm.
引理2[7]对于n阶方阵A,下列诸条件等价
(i)A是次对称矩阵; (ii)AJ是对称矩阵; (iii)JA是对称矩阵; (iv)A=JATJ.
命题1设A为n阶方阵,则
(i)A可以唯一地表示成一个对称矩阵与一个反对称矩阵的和;
(ii)A可以唯一地表示成一个次对称矩阵与一个反次对称矩阵的和.

下证唯一性.设A=B1+C1=B2+C2,其中B1,B2是对称阵,C1,C2是反对称阵.则有
B1-B2=C2-C1,
将等式两边转置得
B1-B2=(C2-C1)T=-(C2-C1),
即B1-B2=O.所以B1=B2,C1=C2.故得证A=As+Aas,其中
(ii)类似(i)的证明可得证,A=Ass+Aass,其中
为了方便研究矩阵的次合同,下面先给出揭示矩阵的次合同与矩阵的合同之间关系的一个重要结果.


BT=(PSTAP)T=PTAT(PST)T.
对上式两边右乘矩阵J可得PTAT(PST)TJ=BTJ,从而有PTATJJ(PST)TJ=BTJ,即
PT(JA)TJ(PT)STJ=(JB)T.
由引理1得PT(JA)TP=(JB)T,转置得PT(JA)P=JB,故JA≃JB.
再证充分性.若JA≃JB,则存在可逆矩阵Q,使得JB=QTJAQ,等式两边取次转置得
BSTJ=QSTASTJ(QT)ST.
对上式两边左乘矩阵J可得JBSTJ=JQSTASTJ(QT)ST,从而有JBSTJ=JQSTJJASTJ(QT)ST,即
JBSTJ=(JQSTJ)(JASTJ)(QT)ST.
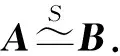
由定理1易得如下结果.

注 由定理1与定理2可知,A与B次合同等价于JA与JB(或AJ与BJ)合同.因此可以把矩阵的次合同关系的判定转化为合同关系的判定;也可以把矩阵的合同关系的判定转化为次合同关系的判定.
定义3设A为n阶方阵,若存在数λ及非零向量α,使得Aα=λJα,则称λ为A的次特征值,α为A的对应于次特征值λ的次特征向量.
由定义3可得,A的次特征值为方程|A-λJ|=0的根,而
|A-λJ|=|J||JA-λE|=|AJ-λE||J|,
即A的次特征值必为JA与AJ的特征值,反之亦然.故有如下结论.
命题2设A为n阶方阵,则数λ为A的次特征值的充要条件是λ为JA或AJ的特征值.

注2 设A为n阶次对称矩阵,则A的次特征值为实数.
接下来,给出次对称矩阵对角化的结论类似于对称矩阵的对角化.
定理3设A为n阶次对称矩阵,则存在正交矩阵,使得A次合同于Λ,其中
λ1,…,λn为A的次特征值.
证因为A为次对称矩阵,由引理2得JA为对称矩阵,故存在正交矩阵P使得
其中λ1,…,λn为JA的特征值.于是有

下面给出次对称矩阵的次合同的充要条件,据此可较简便判定次对称矩阵的次合同关系.
定理4设A与B为n阶次对称矩阵,则下列诸条件等价:
(ii)A与B有相同个数的正次特征值及负次特征值;
(iii)JA与JB有相同的正、负惯性指数;
(iv)AJ与BJ有相同的正、负惯性指数.


且


又由命题2可得


故得证.
对于非次对称矩阵的次合同的判定,结合命题1,有如下结果.


Bss+Bass=PST(Ass+Aass)P=PSTAssP+PSTAassP,
即
Bass-PSTAassP=PSTAssP-Bss,
等式两边取次转置得
PSTAssP-Bss=(Bass-PSTAassP)ST=-(Bass-PSTAassP).
所以Bss=PSTAssP且Bass=PSTAassP.得证.
由定理5易得下述推论.
注 利用定理5判定矩阵的次合同关键在于找出可逆阵P使得Bss=PSTAssP且Bass=PSTAassP,但在A,B已知的情况下,确定可逆阵P比较困难.
2 二阶非次对称矩阵的次合同
文献[2,4]中对二阶非对称矩阵的合同关系给出了实用的判定方法.下面,对于二阶非次对称矩阵的次合同关系,给出简单易用的判定方法.


由文献[4]引理3可得

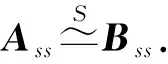
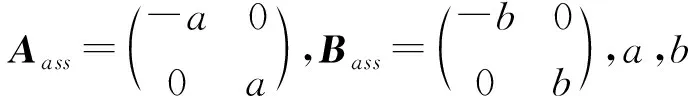
证因为Ass,Bss为次对称矩阵,由定理3可知存在正交矩阵P使得
其中λ1,λ2为Ass的次特征值.

且PJ为正交矩阵.所以存在正交矩阵Q1使得
其中η1,η2为Ass的次特征值.
类似可得,存在正交矩阵Q2使得
其中μ1,μ2为Bss的次特征值.
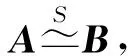
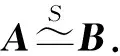
3 应用实例
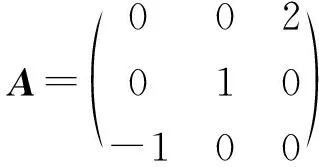
解令|B-λJ|=0得(λ-2)(λ-3)(λ+1)=0,即B有次特征值-1,2,3.又显然A有次特征值-1,1,2,由定理4可得A与B次合同.




解(i) 由题设可得
且Ass的次特征值为1与4;而


下例在文献[1]中已判得A与B合同,在此借助此例说明本文所得结论判别矩阵合同的有效性.

解记
则
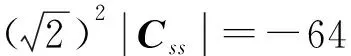
4 结 论
本文主要讨论了实矩阵次合同问题,揭示了矩阵次合同与合同之间的联系,给出了矩阵次合同的一些充要条件.所得结果简单实用,尤其便于判定次对称矩阵及二阶非次对称矩阵的次合同问题.次转置、次对称及次合同等概念是线性代数里转置、对称及合同等经典概念变化与拓展,由此产生了一系列有趣的问题.在教学中,把教材中一些概念及结论进行合理的改变及拓展不仅能开拓学生的视野、激发学生的学习热情还培养了学生综合运用所学知识发现问题解决问题的创新思维与能力,而且有助于提升教师的教学与科研能力.
致谢感谢审稿专家给出的宝贵意见,感谢唐烁老师对论文的多方面的指导.

