浮动基多机协调吊运系统的动力学建模与仿真

赵志刚，赵祥堂，苏程，孟佳东，卫启哲

（兰州交通大学 机电工程学院，甘肃 兰州 730070）

海洋不仅拥有丰富的资源，而且还为国家间的经济交流提供了一条便捷的通道，海洋资源的开采、工程建设及海上救援等作业显得越来越重要。由于传统的船用起重机在效率、负载能力和安全性等方面都无法满足海上吊运作业日益增长的工作要求，研究者提出将柔索并联机器人与船用起重机结合成一种新的吊运装备，即由多台小负载吊运机器人组成，且能够在海上作业的多机协调并联吊运系统［1］。该系统具有可重构性、承载能力强和工作空间大等优点，适合海上空旷的作业环境，且能够根据所需承载灵活调整机器人的数量。

国内外研究人员针对不同的应用场合设计了不同类型的多机器人协调吊运系统，其吊运机器人通常是空中无人机或固定在地面的吊运机械臂，其理论研究已有成熟的体系，并且在实际工程应用中发挥了巨大作用。但水面漂浮式多机协调吊运系统作为一个较新的研究方向，仅有少数学者对浮动环境下绳驱动并联机器人做了初步研究［2］。浮动基多机器人协调吊运系统作为一种较新的多机器人系统，其动力学分析不仅要考虑绳牵引并联吊运系统的动力学和运动学，还要考虑浮动基的动力学，并将二者结合起来得到整个系统的动力学方程组，因此动力学模型的建立成为该系统的难点和重点。

绳牵引并联吊运系统的动力学研究参照了固定基和空中绳牵引并联机构的相关研究。对于空中多机协调吊运系统，赵志刚等［2-3］研究了系统的负载分配问题和系统的运动学和动力学。Jiang 等［4-5］建立了多无人机吊运系统的逆运动学模型对其动力学和逆运动学进行了分析。针对固定基多机协调吊运系统，Wang 等［6-7］通过3 台直角坐标机器人与3 条柔索协调控制被吊物的位置与姿态，对系统的布局、柔索张力及稳定性进行了分析，并且利用实体实验证实了理论分析的结果。Pham 等［8］使用牛顿-欧拉方程建立了平面绳驱动机器人的动力学模型。Pott［9］对建立绳牵引并联机器人动力学模型的各种方法进行了汇总并分析了各方法的特点。Zi 等［10］对起重机末端位置不变情况下3个起重机联合吊运重物的运动学和动力学进行了建模。

对于浮动基机械臂部分的动力学分析则参照了海上平台的研究。Horoub［11］等对一种类Stewart 平台的绳索式海上平台在简谐水波作用下的工作空间以及绳索分布对工作空间的影响进行了研究。Chandrasekaran［12］利用蒙特卡罗方法模拟了波浪，计算了海上浮式结构的波浪力，研究了平台在波浪作用下的动力响应。董艳秋等［13］使用矢量力学原理推导了吊运系统的动力学方程，并探讨了在波浪中被吊物的位移和柔索张力的变化。毛垚飞等［14］研究了由双起重船构成的浮吊系统，分析了波浪和吊运速度对被吊运物晃动的影响。值得指出的是，现有的研究一般只考虑了起重平台对吊物系统的影响，但是吊物系统对平台的影响却研究的很少，未考虑起重平台的运动规律和在波浪中的稳定性。

本文首先建立了三绳索浮动基多机器人协调吊运系统的空间模型，并利用坐标变换法分析了系统的运动学。然后根据刚体动力学和流体力学分别建立了吊物系统和浮动基机械臂的动力学模型。最后通过空间坐标系的转换关系，联合浮动基机械臂和吊物系统的动力学方程，得到了浮动基多机协调吊运系统的动力学模型，并分析了系统包含运动学的动力学问题。

1 系统构型和运动学建模

1.1 系统构型

图1 为拟研究的浮动基多机协调吊运系统的空间构型，系统由浮动基座、机械臂、绳牵引并联吊物系统（柔索和负载）组成。机械臂采用三自由度关节型机械臂，连杆1可绕z轴转动，连杆2和连杆3可以绕其关节上下转动，3台机械臂分别固定在3个浮动基座上构成浮动基机械臂。吊运过程中，可以改变浮动基座和机械臂末端的位置以及柔索长度使负载按照期望的轨迹运动，柔索的变化由吊机末端的驱动装置进行操纵。

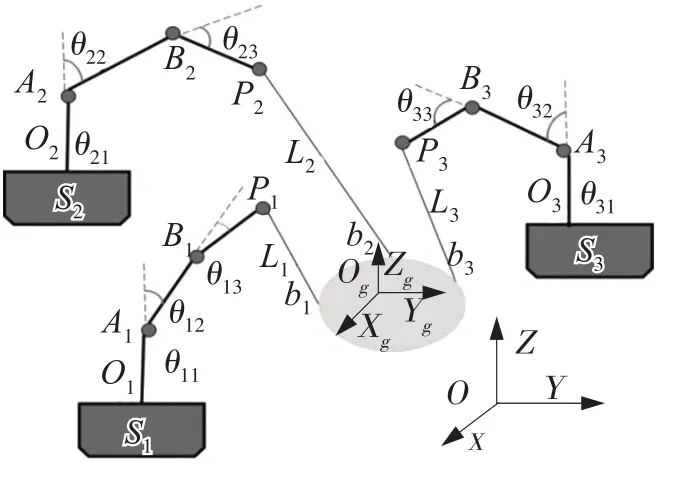
图1 浮动基多机协调吊运系统空间构型Fig.1 Structure of the floating multi-robots coordinated towing system

结合系统空间结构设定下列坐标系。取水平面上一点建立惯性坐标系{O}，在浮基的质心处建立坐标系{Osi}，在机械臂底部建立坐标系{Oi}，在负载中心建立坐标系{O g}。机械臂的杆长为(ai1,ai2,ai3)，转角为(θi1,θi2,θi3)，机械臂末端与柔索的连接点记为Pi，柔索与负载的连接点记为bi，柔索的位置矢量记为Li。由于整个系统由3 台吊机组成，故i=1,2,3。

由于实际的吊运系统结构复杂，在进行分析时需要作如下假定：

1）浮基为质量均匀的刚体，不考虑各自由度之间的耦合作用；假设负载为质量均匀的刚体。

2）作用在浮基上的波是线性规则波，暂时不考虑波浪非线性效应的影响。

3）机械臂结构刚度足够强，暂不考虑机械臂受力后的弹性振动与形变。绳索受力时将其视为刚体，忽略其弹性形变以及质量。

1.2 浮动基机械臂的运动学模型

图2为浮动基机械臂的结构简图，假设3台浮动基机械臂结构相同，选择其中一台为例进行运动学建模。利用卡尔丹角来表示浮基的运动，浮基绕3个坐标轴的旋转(αi,βi,γi) 表示浮基的横摇、纵摇和回转运动。浮基在空间内的位置(xsi,ysi,zsi)表示它的横向、纵向和垂向运动。

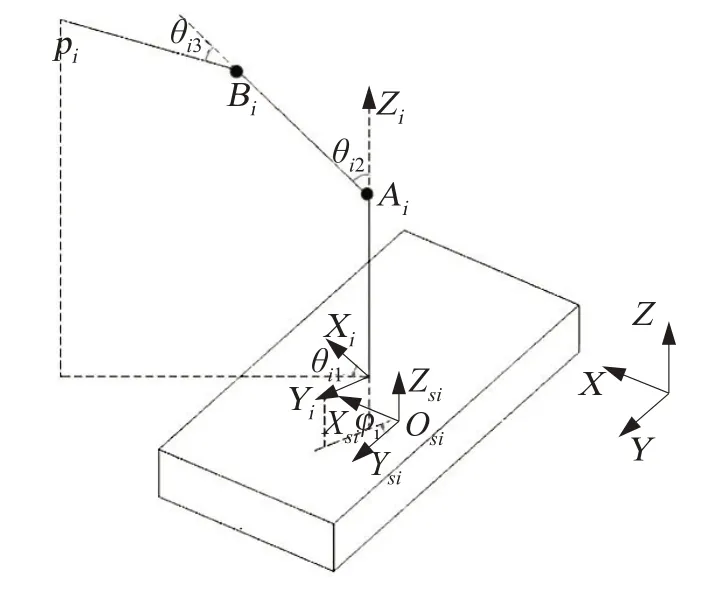
图2 浮动基机械臂结构Fig.2 Structure diagram of floating robot

在机械臂坐标系{Oi} 中，吊机末端的齐次坐标为：

式中：si1、si2、si3和ci1、ci2、ci3为机械臂3 个关节角的正弦值和余弦值；ai1、ai2、ai3为机械臂的杆长。

在惯性坐标系{O}中，吊机末端的齐次坐标为：

式中：R*为机械臂坐标系{Oi} 与浮基坐标系{Osi} 间的变换矩阵；R为浮基坐标系{Osi} 和惯性坐标系{O} 间的变换矩阵。

在惯性坐标系{O}中，联立式（1）和式（2）可求出吊机末端和浮基之间的运动关系。

1.3 吊物系统的运动学模型

在惯性坐标系{O}中，机械臂与柔索连接点的位置为Pi(xPi,yPi,zPi)，负载与柔索连接点的位置为Bi(xBi,yBi,zBi)，负载质心的位置向量为r=[x y z]T。在负载坐标系{Og}中，负载与柔索连接点的位置为bi，则可得关系式：

式中：RG为负载坐标系{Og}相对于惯性坐标系{O}的旋转变换矩阵：

式中：s为sin函数，c为cos函数。

由Pi和Bi得到绳长为：

根据浮基和机械臂的运动规律，联立求解式（1）～（5），可以得到吊机末端坐标(xpi,ypi,zpi)、实时绳长Li、柔索连接点坐标(xbi,ybi,zbi) 和负载位置(xq,yq,zq)的关系式，即吊运系统的运动学方程。

2 系统动力学建模

由于柔索只能对负载实施单向张力约束对控制柔索式多机协调吊运系统增加了难度，因此建立正确的系统动力学模型是研究浮动基多机协调吊运系统动力学特性的前提。浮动基多机协调吊运系统由绳牵引并联吊物系统和浮动基机械臂两部分组成，分别建立这两部分的动力学方程，并将其联合得到浮动基多机协调吊运系统的动力学模型。

2.1 浮动基机械臂的动力学模型

浮动基机械臂由固定在浮动基座上的关节型机械臂构成，分析动力学时将浮动基和机械臂作为同一个刚体进行分析，且忽略机械臂位姿变化对浮动基位姿的影响。浮动基受到浮力的影响，其位姿与浮动基机械臂受到的绳拉力相关，而浮动基的位姿又与机械臂末端位置有关，因此还需要对浮动基机械臂的动力学进行分析。通过分析机械臂的关节力/力矩，将浮动基机械臂和绳牵引并联吊物系统的动力学联立。

2.1.1 机械臂关节力/力矩分析

吊物系统的柔索外力和机械臂内力会转化为作用于浮基的力/力矩，在吊运过程中可能会导致浮基倾覆，因此分析并验证在静态受力情况下机械臂关节上的约束力/力矩很有必要。

本节应用牛顿-欧拉迭代动力学方程［15］，计算吊机末端受到的柔索拉力传递到浮基上的力/力矩。以关节1 为例，分析作用在机械臂关节处的力与力矩，其表达式为：

式中：Mg1、vMm1、aMm1和分别为由机械臂所有连杆的质量、关节角速度、关节角加速度和机械臂末端柔索拉力引起的约束力与力矩［15］。

在静态受力情况下，机械臂各个关节角速度与角加速度均为零，关节1 受到由机械臂连杆引起的约束力和力矩。运用ADAMS软件对机械臂在静态受力情况下的动力学进行仿真。仿真结果表明：根据建立的动力学方程式（6）得到的关节1 上的约束力/力矩与ADAMS 软件的仿真结果一致，证明了方程的正确性。

2.1.2 浮动基的动力学模型

根据分离建模的思想［16］，将整个浮式吊运系统受到的干扰力（矩）作为外力附加到浮基运动数学模型上。按照物理意义分解为流场对浮基的作用力、机械臂对浮基的作用力和吊物系统对浮基的作用力。

严格来说，应该分析浮基在波浪中的六自由度运动。然而，随着自由度的增加，分析问题的难度也会加大。最简单的方法是研究浮基的升沉运动，即在波浪扰动力Fw的作用下，建立浮基在波浪力（波浪激励力和辐射力）、静水恢复力和阻尼力等其他载荷联合作用下的运动方程为：

式中：Mzz=mG+λzz；Czz=ρSw；mG为浮基质量；λzz为附加质量系数；为沿Z向的加速度；ρ为水的密度；Sw为水线面面积；NZZ为阻尼系数；Fzz和Tzz分别为浮基所受波浪扰动力和柔索张力在Z向的分力。

类似地可以按照上述假设及方法建立其余自由度上的运动微分方程为：

式中：M、N、C、F和T（M）依次为惯性力、阻尼力、恢复力、波浪扰动力和吊物系统对浮基的作用力（力矩）系数，它们的下标为所在自由度。

2.2 吊物系统的动力学模型

图3 为吊物系统的结构简图。为方便推导重新建立坐标系，将机械臂坐标系视为惯性坐标系，并将吊物系统模型简化为球摆模型。其中点P为吊点（机械臂的末端点），点Q代表负载，柔索长度为l。

图3 吊物系统示意Fig.3 Diagram of the towing system

吊物系统中柔索的位置利用面内角θx和面外角θy来定位。假设初始状态柔索与z轴平行，负载由状态1至状态2的运动过程中，柔索绕P点旋转了θx；当负载由状态2 至状态3 的运动过程中，柔索绕P点旋转了θy。则负载的位置可以表示为：

式中：m为负载质量；T为柔索的动张力。

对式（10）整理后得到：

式（11）和式（12）即为以θx、θy为广义变量的球摆模型的运动方程组。对式（10）整理后得到柔索张力表达式为：

3 动力学分析与求解

系统的动力学分析就是在运动学的基础上，根据已知机构所受的外力，计算目标机构所受的约束力以及求解机构的运动。系统动力学的研究和运动学研究相类似，也分为正向逆向动力学问题。

令负载的位姿向量为VP=[xq,yq,zq,θx,θy]T，各机械臂关节角和绳长变量组成的向量定义为VJ=[θi1,θi2,θi3,Li]T，浮动基的运动变量组成的向量定义为VM=[xsi,ysi,zsi,αi,βi,γi]T。

3.1 正向动力学分析

正动力学问题为已知系统的关节变量，将浮基的运动视为激励，再将这一激励传递到吊物系统中，求解负载的运动。故正动力学问题可以简化为：当浮动基在特定运动状态VM下，已知系统的关节向量VJ，求解柔索拉力向量T和负载的位姿向量VP。详细求解步骤为：

1）已知系统结构参数和空间布局，给定浮基的运动规律VM和机械臂的运动状态VJ。假设负载的初始位置为(40,23,22)，吊运的目标位置为(40,23,30)，以吊物系统最大动力响应为切入点，将浮基的运动视为基座激励施加在吊机末端。

由于系统的空间相对位置可依据不同的应用场景进行实时设计，每台浮动基机械臂随波浪产生的运动各不相同。基于前人对非线性系统的相关研究［17］，假设浮基处于规则波环境中，吊机末端受到的激励为：

2）根据吊物系统动力学模型的推导过程，联合式（11）和式（12）求解得到负载的摆动角θx和θy，然后求解式（13）获得柔索的动张力T。

3）由吊机末端在惯性坐标系中的运动轨迹和浮基的运动规律，利用式（1）和式（2）可以求出吊机末端的位置(xpi,ypi,zpi)，再将吊机末端位置代入式（9）得到负载的位置(x q,yq,zq)。

3.2 逆向动力学分析

逆动力学问题为已知系统的关节变量，将负载的摆动视为吊机末端的激励，再将这一激励传递到浮基上，求解浮基的运动。故逆动力学问题可以简化为：当负载在特定运动状态VP下，已知系统的关节向量VJ，求解机械臂各关节的约束力和浮动基的运动状态VM。详细求解步骤为：

1）已知系统结构参数和空间布局，根据负载的期望运动轨迹，即负载经过60 s 的上升后静止在期望位置，且上升过程中的运动轨迹为光滑曲线。假设负载的期望运动轨迹为：

取负载的空间位置(x q,yq,zq)和摆角θx、θy的最大值作为输入，求解式（13）获得柔索的张力T。

2）根据柔索张力和柔索的空间位置，将柔索张力在惯性坐标系上3 个方向的分量TX、TY、TZ与浮动基机械臂任意时刻的空间位置结合，由式（6）可求得机械臂关节1上的作用力和力矩。

3）将吊物系统对浮基的作用力Txx、Ty、yTzz和力矩Mθθ、Mφφ、Mψψ代入式（7）和（8），利用四阶龙格库塔法求解浮基的运动规律VM。

4 数值仿真分析

为了验证前述动力学方程的合理性，对系统进行数值仿真分析。设定浮动机械臂的初始参数，其中浮动基座的构型参数为：L=10 m、W=3 m、H=4 m。机械臂的初始构型参数为：ai1=15 m、ai2=20 m、ai3=20 m、xi=0 m、yi=0 m、zi=2 m。3 台浮动基机械臂在空间中的位置为品字形正三角形结构。浮动机械臂静止于水面时浮基吃水深度为2 m，吃水量为1.0 × 105kg，流体密度ρ=在波浪工况下，选择三级海况作为系统工作时的外部环境条件，波速波高为2 m，波长为10 m，浪向角0。吊运系统参数如表1所示。

表1 系统参数Table 1 Parameters of system

吊运系统的工作过程可以分为2个阶段：第1个阶段为0～60 s，3 条柔索均以0.05 m/s的速度匀速收缩；第2 个阶段为60～120 s，系统进入自平衡阶段，柔索收缩速度及机械臂关节角转速均为0。

在实际工况中，浮动基座内通常都配备了动力定位系统，用来控制浮基的横荡、纵荡和回转三自由度运动，可以抵消浮基的基座扰动。分别以系统的正向动力学和逆向动力学问题为研究对象，在波浪作用下对浮基、负载和柔索的运动进行了时域仿真分析。为了清楚地看到时域响应的传递过程，只截取了一段有代表性的时域响应曲线，仿真结果如图4～8所示。

图4 负载位移Fig.4 Displacement of load

4.1 正向动力学的仿真

在起吊过程中柔索匀速收缩，由于负载运动会受到浮基运动的影响，负载变速上升。而当柔索停止收缩时，负载随着浮基的运动而运动，但在考虑波浪扰动时，由于柔索张力的往复变化，导致吊物的摆动加剧。从图4 可以看出，最终Z向平衡位置为30.18 m，X和Y方向偏离平衡位置的最大距离分别为0.76 m和0.53 m。在给定激励频率的条件下可以得出负载的面内角和面外角，由图5可以看出面外角与面内角的变化趋势不同，对面内角而言，在吊运的过程中摆动先增大后减小，没有规律可循，最大摆角不超过1.1°；对面外角而言，可以看出初始阶段摆动迅速增大，随后面外角有逐渐减小的趋势，呈现周期性变化。在系统自平衡阶段，面内角远大于面外角。

柔索的动张力曲线如图6 所示，随着柔索收缩，柔索张力不断增加；由于浮基和吊物系统的相互影响，系统内能量不断抵消，张力曲线更加平稳。当柔索停止收缩时，浮基进入自平衡衰减状态，吊运系统并未出现失效。

图6 柔索张力Fig.6 Tension of cable

4.2 逆向动力学的仿真

图7 和图8 分别是浮基的线位移和角位移的变化曲线。从图7 可以看出，浮基在流体的垂向升力和浮力的作用下会造成较大的横向和垂向位移，但横向位移在短时间内会趋于平稳，垂向位移由于水流涡激升力的原因会长时间往复振动。最终平衡时，Y方向的位移达到 0.43 m，Z方向的位移达到0.12 m。由图8 可以看出，在起吊前横摇运动幅值较小，而在起吊过程中，浮基横摇运动幅值急剧增大。当柔索停止收缩时，浮基的运动逐渐过渡到简谐运动。浮基的横向位移最大为0.72 m，横摇角度最大为24°，这给负载的吊运带来了很大的困难。

图7 浮基线位移Fig.7 Displacement of floating foundation

图8 浮基角位移Fig.8 Angle displacement of floating foundation

5 结论

1）目前，大多数的船用起重机属于回转旋臂式起重机。本文将工业机器人和起重系统二者结合，提出一种浮动基多机协调吊运系统，它不但具备机器人的结构特点而且还具有起重机的工作方式，同时也为海上吊运设备的研究提供了思路。

2）浮动基座、机械臂和吊物系统三者组成复杂的动力学系统，利用动力学和流体力学理论分别建立了吊物系统和浮动基机械臂的动力学模型。通过2种方法的组合使用解决了刚柔耦合机器人系统自由度太多、难以采用传统单一方法建立动力学模型的问题。

3）现有的研究一般只考虑了起重平台对吊物系统的影响，但是吊物系统对起重平台的影响却研究的很少，未考虑起重平台在波浪中的运动规律。通过正逆动力学分析很好地解决了这个问题。

4）本文在进行数值计算时，并未考虑吊运过程中造成的负载摆动与浮基运动引起的负载摆动是相互耦合的，这与海上实际有一定差距，需要在以后的研究中加以改进，并进一步开展负载的防摆控制研究。