基于MATLAB的某型履带吊管机吊物系统动态特性分析
宋秋红, 王皓辉, 徐少蓉, 杨绍杰
(1. 上海海洋大学工程学院,上海 201306;2. 上海彭浦机械厂有限公司,上海 200072)
基于MATLAB的某型履带吊管机吊物系统动态特性分析
宋秋红1, 王皓辉1, 徐少蓉1, 杨绍杰2
(1. 上海海洋大学工程学院,上海 201306;2. 上海彭浦机械厂有限公司,上海 200072)
吊管机在外部工况激励的作用下会产生危险的大幅摆动,不仅会降低施工的吊装精度,严重时还会引起吊物和结构的碰撞。因此对吊管机进行吊物系统动态特性分析对吊管机的作业安全具有重要的意义。依据吊管机的工作环境,总结和对比国内外的相关研究。建立吊物系统的数学模型,推导吊管机吊物系统的非线性动力学方程,并利用 MATLAB进行吊管机吊物系统的数值分析。结果可以看出吊索长度、外部激励频率、吊物的升降速度分别对吊物系统的动态响应、吊物摆振、吊物的面内外摆角产生影响。
吊管机;非线性方程;动态分析;MATLAB
吊管机是管道工程中至关重要的专用工程机械设备之一,其主要作用是在管道施工中,负责管道的铺设、对接以及下沟等作业[1],如图1所示。吊管机工作环境复杂,行驶路况恶劣,作业时当受到外部激励影响,整车的稳定性下降,可导致吊管机翻车,造成设备的损坏与人员的伤亡,因此对吊管机进行吊物系统动态特性分析,对吊物的摆振进行控制与预测将对吊管机的作业安全具有重要的意义。
参考国内外有关吊管机吊物系统的文献后发现,吊管机的总体运动是各种非线性运动的集合,而作为重要组成部分的吊物系统,也包含着极其繁琐的非线性特征。Elling和 McClinton[2]将起重机的吊物系统简化为球型的钟摆运动,仅仅受基座激励影响。研究表明,吊物系统的动力响应要发生谐振现象,需要激励频率接近或等于吊物系统吊索的固有频率或者接近 1.5倍的系统固有频率。Henry等[3]建立了一个平面单摆模型,是通过一个质量忽略不计的刚性吊索以及集中质点所组成的,其实验结果表明,通过控制摆幅可以大幅度减小吊物的摆动角度。董艳秋和韩光[4]利用计算得出整机的运动传递到吊物吊点处的矩阵方程,并研究吊物系统的非线性动力响应,然后逐一改变其摆角、吊索长度、动张力、吊物质量以及起吊速度等参数,研究平面内吊管机吊物系统的动力学非线性关系。
通过上述文献研究不难发现,国内有关吊物系统动态响应方面的研究较之国外欠缺,实验验证也不多,而国外在相关领域上的研究更趋成熟。以上几个吊物系统模型的研究,均考虑了非线性特性,为了方便研究均在不同程度上简化了吊物系统,并未以系统的推论作为基础。
本文在参考了相关文献的基础上,推导出了吊管机吊物系统的非线性动力学方程,并以此作为理论基础利用MATLAB进行吊管机吊物系统的数值分析。
1 吊物系统数学模型建立
吊物系统包含了极其复杂的非线性特征,不利于分析,为了研究的方便,需对吊物系统进行适当的简化:
(1) 设吊物为一质点;
(2) 忽略吊索的质量,并且不考虑其弹性伸缩量;
(3) 将吊臂看成刚性物体,不考虑其弹性形变量;
(4) 外界对吊物系统的影响可以简化为吊物点在参考坐标系3个方向的简谐激励。
由于是对吊物系统进行动态特性分析,因此对吊物系统做类似的简化能够基本反映出吊管机吊物系统动态特性的真实性,不会对结论造成较大影响[5]。
1.1建立吊物系统的动力学方程
如图 2所示,创建吊管机吊物系统模型。图中 O点即为惯性参考系(xo,yo,zo)的原点即固定点;B点即为吊臂悬挂吊物的吊点;C点即为吊物,设其质量为m;BC即为吊索,设其长度为l,质量忽略不计并且不考虑弹性伸长量。

图2 吊管机吊物系统模型
假设开始时,吊索与z轴的方向平行,将吊索绕着B点且平行于x轴的轴线转动α角度,称为面外角;而将吊索绕着B点且平行于惯性轴y轴的轴线转动β角度,称为面内角。这样就形成了(x1,y1,z1)坐标系。
吊索BC在惯性参考系(xo,yo,zo)中的相对位置由面外角α与面内角β来确定。吊点B在惯性参考系(xo,yo,zo)中的相对位置由(xB(t),yB(t),zB(t))来确定,C点在惯性参考系(xo,yo,zo)中的位置向量由rC来表示,吊物C在惯性参考系(xo,yo,zo)中的相对位置由(xC(t),yC(t),zC(t))来确定。

其中:

从方程组式(2)可以推得:

考虑到吊物的升降运动,对上面的方程组式(3)左右两边同时对时间求一阶导数,得到吊物的升降速度为:

在实际的操作过程中,吊索会因为各种外在因素在吊点 B处产生摆动、扭转从而变形产生弹性阻力,为了分析以及后续数据处理的方便,则设吊索在吊点 B处所形成的弹性阻力简化为面外和面内的弹性力 k0α(t),k1β(t)(其中 k0,k1为弹性系数)。并且设(x1,B,z1)平面位置的势能为零势能面,则系统势能的公式即可表示为:
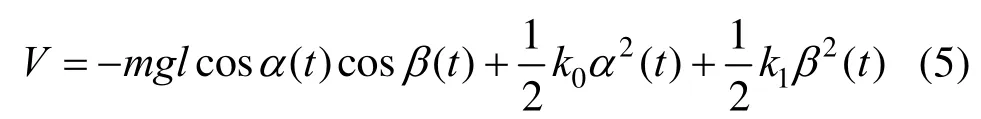
系统的动能为:
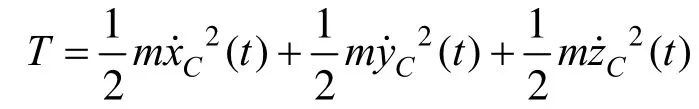
所以推得系统的拉格朗日函数为:
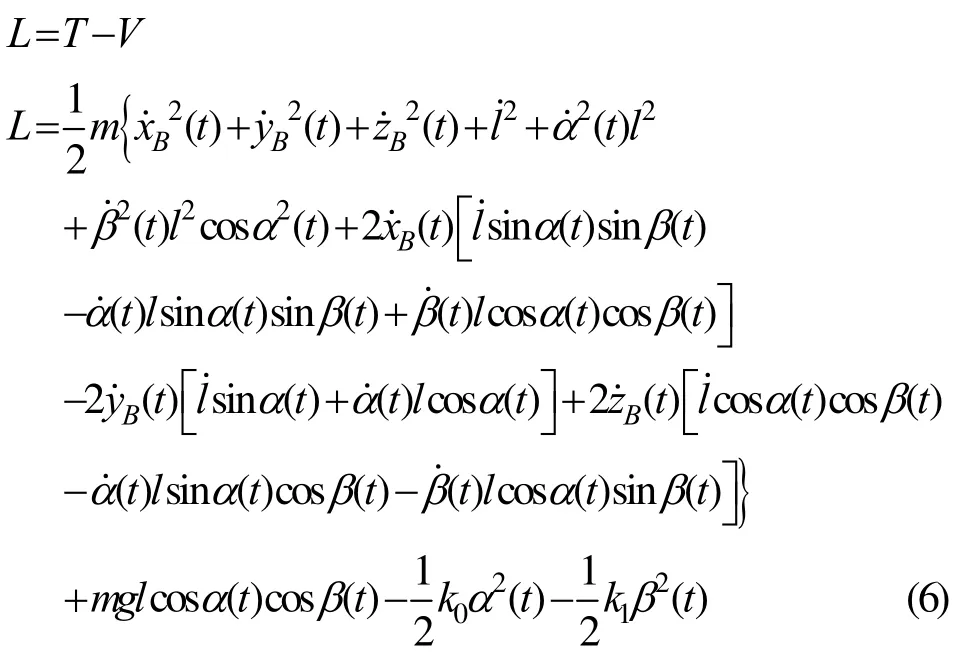
由拉格朗日方程:

可以推算整理得到吊物系统的非线性动力学方程为:1.2吊索动张力响应
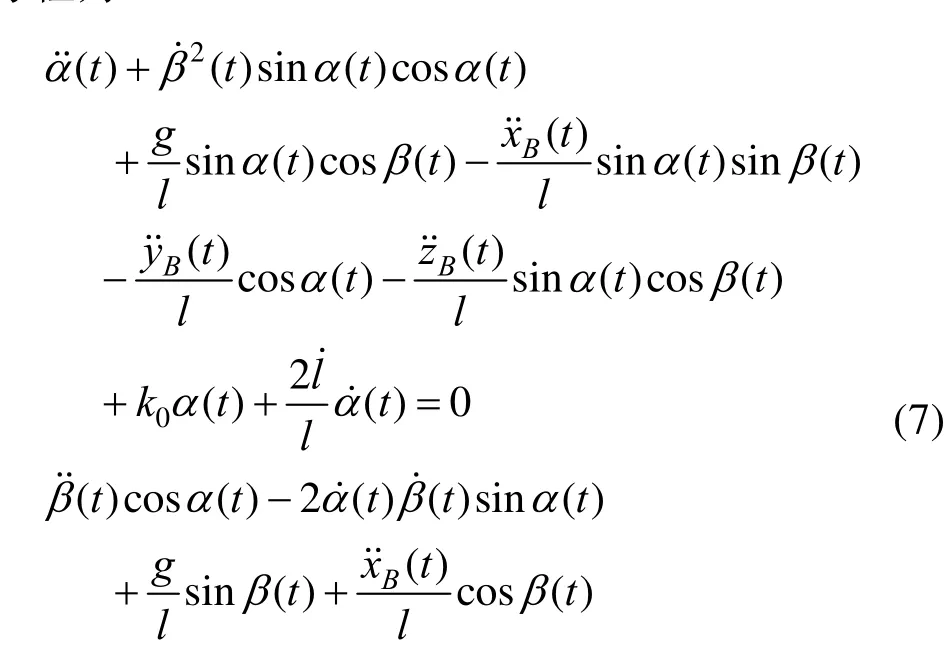
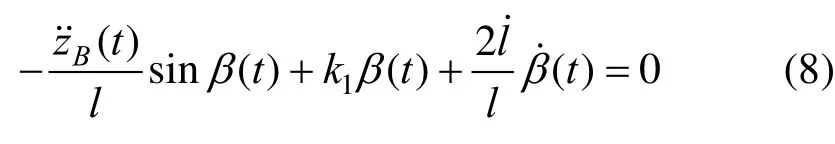
吊物的运动方程可以根据牛顿第二定理得到:
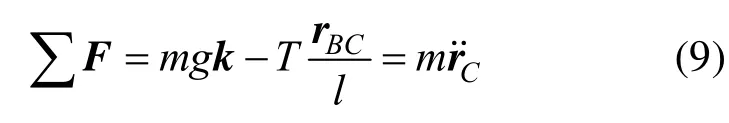
这里设T为吊索张力。将式(2)代入式(9),经整理得:
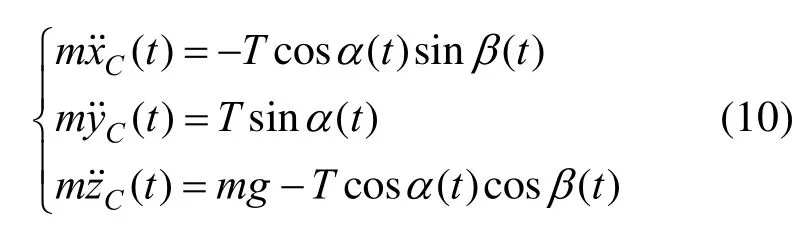
为了求吊索的张力,在式(10)等式两边同时乘以cos、sin项:

将式(12)减去式(11),再减去式(13),整理可得:
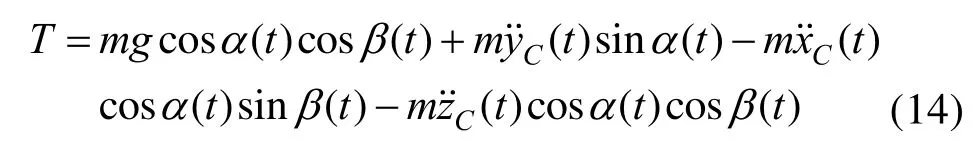
对方程组式(3)左右两边同时对时间求二阶导数便可以得到吊物的加速度:

将式(15)代入式(14),经整理可得吊索张力为:

由理论力学可知当吊物静止处于平衡状态时,外力合力为零,因此平衡时的吊索张力为:T=mg,而当吊物起升、下降运动时,平衡被打破,吊索张力将逐渐变大。而将吊物运动状态时的张力与处于平衡状态时的张力相减,所得差值,即为吊索的动张力,记为 TD,则吊物的动张力的方程表达式为:
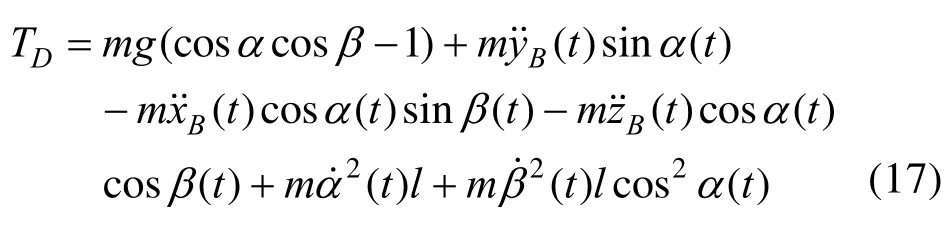
通过式(17)可以看出动张力TD是关于自变量时间 t的函数。可以通过式(7)和式(8)得到面外角α(t)、面内角 β(t),从而推得吊物系统的吊物角速度以及吊点处的加速度向量,以求得吊索的动张力响应。
2 吊管机吊物系统动态响应数据分析
解析吊管机吊物系统的非线性动力学方程式(7)和(8),可发现若用原始的方法获得精确的答案是非常困难的,只能依靠数值方法求解。下面将运用MATLAB软件,对系统的非线性动力学方程进行仿真模拟研究[6-7]。
2.1吊点B的运动
通过吊管机吊物系统的非线性动力学方程式(7)和(8)可以发现吊物的摆动,即面外角、面内角与吊点B的运动与xB(t)、yB(t)和zB(t)有关。
通过非线性振动的相关研究可得知,xB(t)和yB(t)均为附加项,因此系统的最大响应值,将在其附加项的频率接近吊物的固有频率Nω时产生。zB(t)为参数激励项,所以系统的最大响应值,会在参数激励项的激励频率接近于 2倍的吊物系统固有频率时出现,而且在此时刻最容易发生参变激发现象[8-9]。
吊物系统的动态响应与系统的各项参数、外部的激励频率包括幅值等因素相关,若将这些因素以不同的方式进行参数组合,就可得到不同程度下的动态响应结果,这里所要考虑的是在条件最为不利的情况下(极端工况条件)的激励最大系统响应,因此在吊物的吊点 B(xB(t),yB(t),zB(t))处,沿xo、yo、zo方向施加正弦激励,如式(18):

其中,xo、yo、zo三个方向上的幅值分别为Ax、Ay、Az,而xo、yo、zo相应方向上的激励频率分别是xω、yω、zω。则吊点B在各个方向上加速度的分量可由相应方向上的幅值和激励频率表示,即为:

通过上述分析可知,当xω=yω=Nω;zω=2Nω时,系统将会产生最大响应。其给定初始条件为吊点 B的 xo、yo、zo三个方向的激励幅值分别为0.500 m,0.250 m,0.125 m。
2.2吊索长度对吊物系统动态响应的影响
设置初始条件,激励幅值设置为:Ax=0.500 m,Ay=0.250 m,Az=0.125 m;激励频率为:xω=yω= 1.4,zω=2.8,在1 000 s内吊点B的各方向加速度分量变化如图3~5所示:

图3 ?(t)在1 000 s内的变化
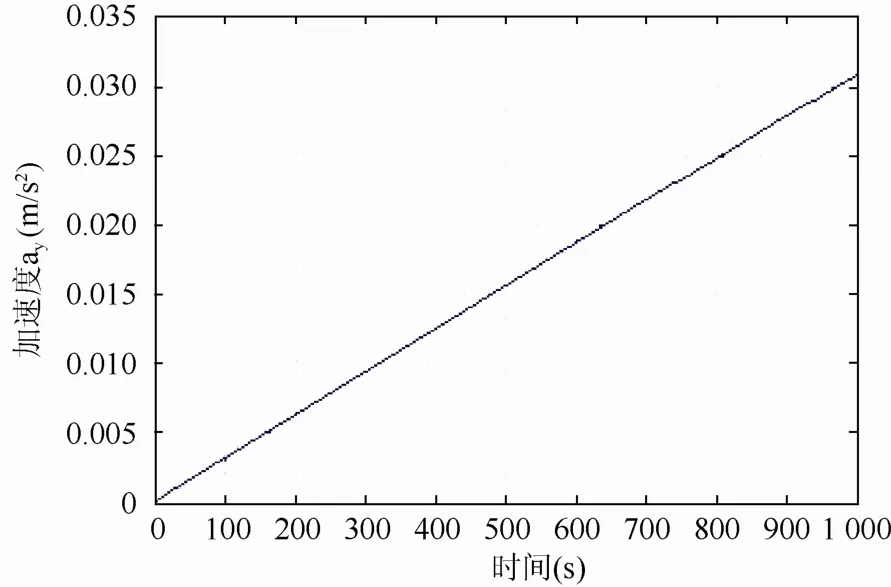
图4 ?(t)在1 000 s内的变化

图5 ?(t)在1 000 s内的变化
为了研究吊索长度对吊物的影响,在不考虑吊物的升降运动时,设弹性系数k0,k1均等于0.01,选取不同吊索的长度分别为:2 m,4 m,6 m,8 m时,1 000 s内反应吊物系统动态响应的面外角α和面内角β的变化情况如图6~9所示。
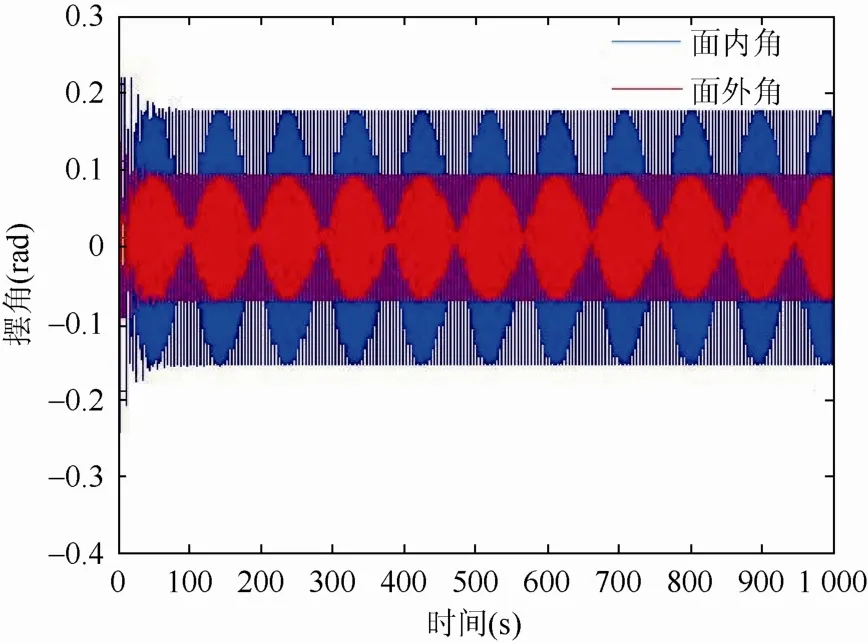
图6 l=2 m时面外角、面内角响应
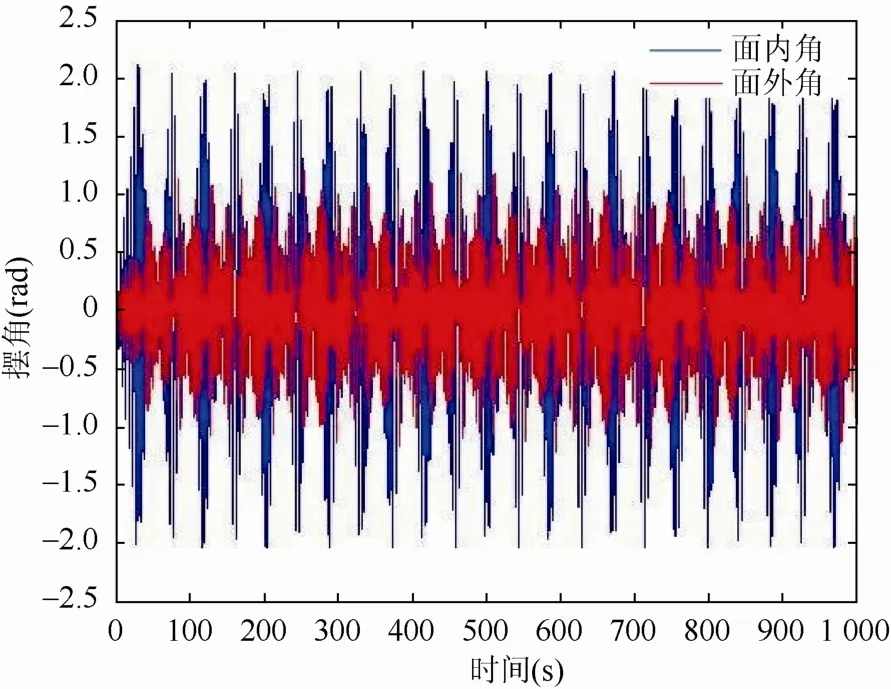
图7 l=4 m时面外角、面内角响应
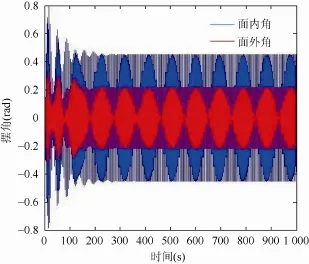
图8 l=6 m时面外角、面内角响应

图9 l=8 m时面外角、面内角响应
2.3激励频率对吊物系统动态响应的影响
设初始条件:激励幅值Ax=0.500 m,Ay=0.250 m,Az=0.125 m;取吊索长度l=4 m,则系统的特征频率取ωN=1.4;取不同激励频率(激励频率为1倍的特征频率之间):0.3ωN,0.6ωN,0.9ωN,1.0ωN,1.3ωN,1.6ωN时,吊物摆角的动力响应情况如图10~15。
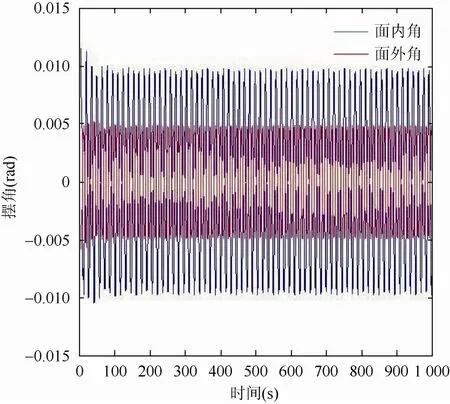
图10 ω=0.3ωN时面外角、面内角响应

图11 ω=0.6ωN时面外角、面内角响应
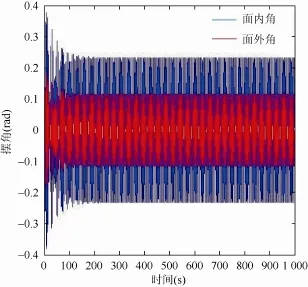
图12 ω=0.9ωN时面外角、面内角响应
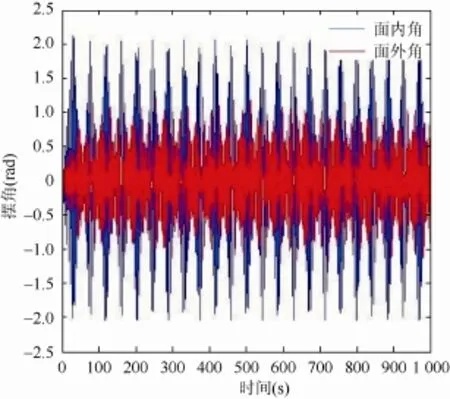
图13 ω=ωN时面外角、面内角响应

图14 ω=1.3ωN时面外角、面内角响应
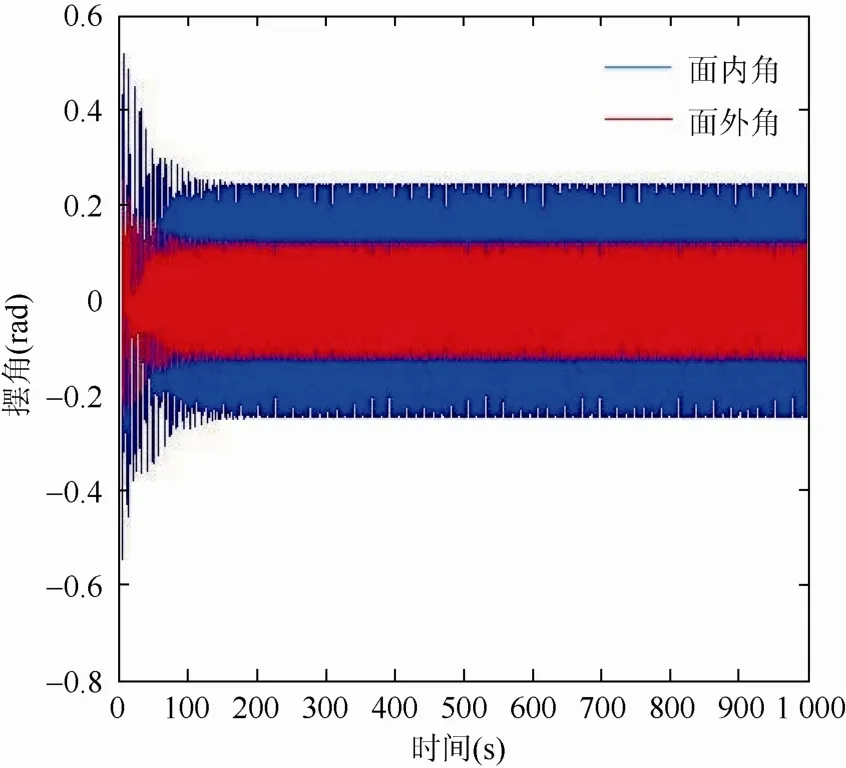
图15 ω=1.6ωN时面外角、面内角响应
由图 10~15可看出,改变激励频率时,若激励频率远离系统特征频率,则吊物系统的面外角、面内角偏小,随着激励频率的增加,当激励频率接近系统特征频率时,吊物系统的面外角、面内角达到最大,即吊物系统的动态响应最大,之后随着激励频率继续增加,吊物系统的面外角、面内角又逐渐减小。
若继续去除吊索在吊点处的弯曲刚度影响因素,即设k0,k1为0,在图12所示情况下,吊物面外角、面内角响应情况如图16所示,显然图16中吊物摆角幅值比图12中摆角幅值要大。这说明吊点处吊索弯曲刚度对摆角起到了抑制作用。
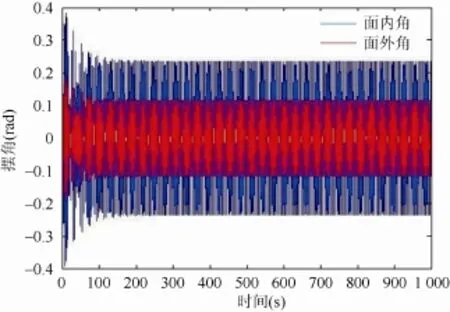
图16 k0=k1=0,ω=0.9ωN时面外角、面内角响应
2.4吊物的升降运动对吊物系统动态响应的影响
在吊物起升过程中,设吊索长度的初值为8 m,而吊物起升速度分别依次为 0.13 m/s、0.14 m/s;在吊物下降过程中,设吊索长度的初始值为1 m,而吊物下降速度分别依次为–0.090 m/s、–0.125 m/s。运用MATLAB求算不同升降速度下吊物面外角、面内角的状况如图17~20所示。

图17 l˙=0.13m/s 时面外角、面内角响应
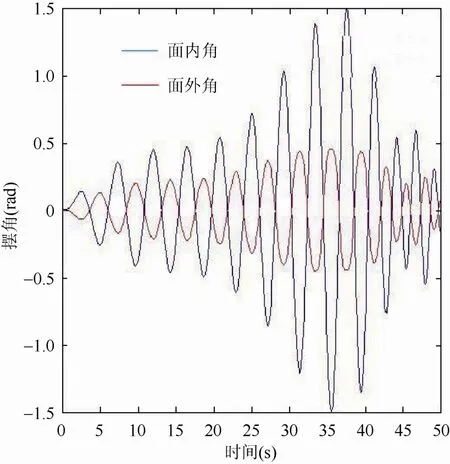
图18 l˙= 0.14m/s 时面外角、面内角响应
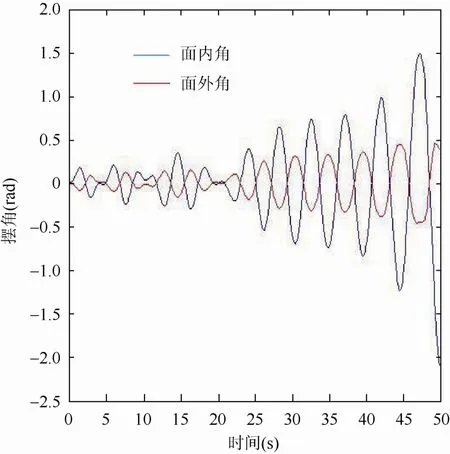
图19 l˙=−0.09m/s 时面外角、面内角响应
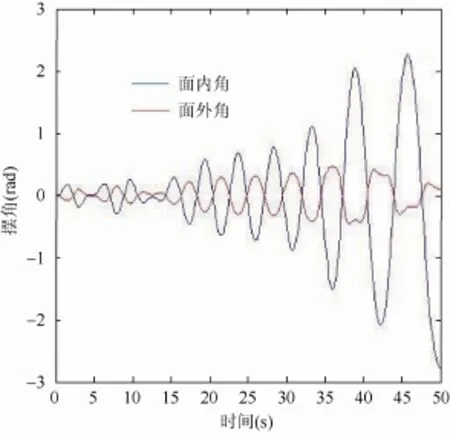
图20 l˙=−0.125m/s 时面外角、面内角响应
对比图17和图18可以得出:在起升过程中,吊物的起升速度与吊物的系统响应呈反比,且起到抑制作用,吊物起升速度越大,则吊物的面外角、面内角却有减小的趋势。
对比图19、20可以得出:在吊物下降的过程中,吊物下降的速度与吊物的系统动态响应呈正比、起到帮助作用,随着吊物下降速度增大,吊物的面内角、面外角也呈现出逐渐增大的趋势。
此外,还观察到,在吊物升降过程中,吊索长度的变化也将影响到系统的固有频率变化,当吊索长度接近4 m时,吊物系统的固有频率接近于外部激励频率,这时吊物的面内角、面外角有明显增大的趋势。
2.5吊物面内外部激励对面外角的影响
为了便于观察吊物面内外部激励对面外角的影响,仅对吊点B施加xo方向的激励,即:
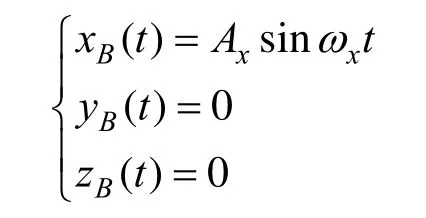
这里 Ax=0.5 m,吊索长度 l=4 m。激励频率ωx(激励频率为 1倍的特征频率之间)分别取0.8ωN,ωN,1.2ωN。
运用MATLAB软件使用数值方法解算动力方程时,为了研究外部激励对响应的影响,需要最初在外加给予系统一个很小的初始扰动,因此初始值设定为α=0,β=0.001,如图21~23所示。

图21 ωx=0.8ωN时面外角、面内角响应

图22 ωx=ωN时面外角、面内角响应
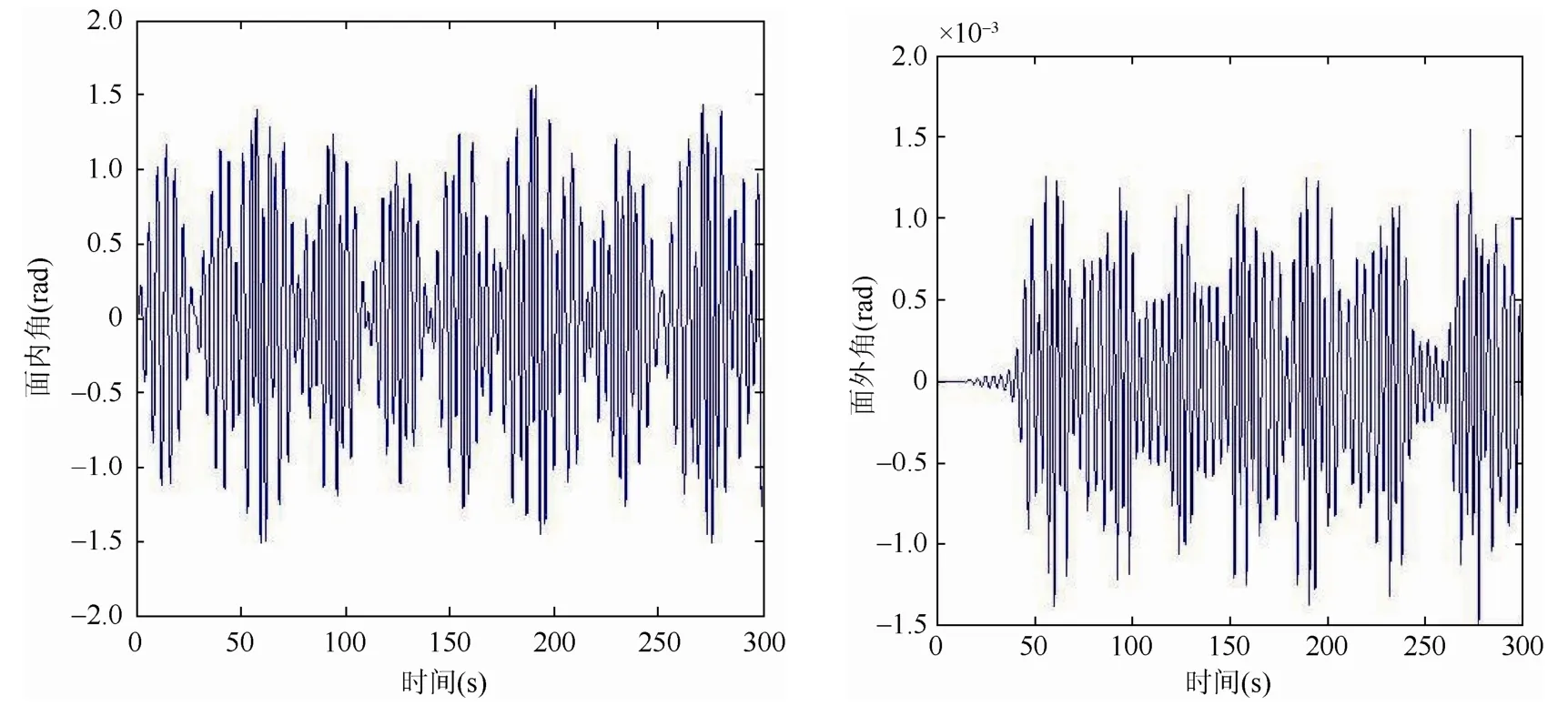
图23 ωx= 1.2ωN时面外角、面内角响应
从图 21~23可以看出,当激励频率跟吊物系统固有频率相差很大时,吊物面外角受面内的激励影响是很小的,但若激励频率接近于吊物系统的固有频率时,此时面内的激励对吊物面外角将产生极大的影响。
3 结 论
通过运用数学公式及理论可成功推算出吊物系统的非线性动力学方程。而后运用MATLAB平台,通过改变吊索的长度、不同的外部激励频率以及吊物的升降速度逐步分析和研究了吊物系统在外部激励下的响应特性[13]。分析研究表明:通过改变吊索长度可以改变吊物系统的动态响应;纯粹的外部激励会导致面内、面外角产生较大变化;改变吊物的升降速度可以改变吊物的面内、面外摆角;而吊点处吊索的弯曲刚度则对吊物系统的面外角、面内角起到抑制的作用。
[1] 《2012年国内外油气行业发展报告》课题组. 全球油气行业发展2012年回顾与2013年展望[J]. 国际石油经济, 2013, (Z1): 30-32.
[2] Elling R E, McClinton A T. Dynamic loading of shipboard cranes [C]//IEEE International Conference on Engineering in the Ocean Environment, USA, 1973: 174-177.
[3] Henry R J, Masoud Z N, Nayfeh A H, et al. Cargo pendulation reduction on ship-mounted cranes via boom-luff angle actuation [J]. Journal of Vibration and Control, 2001, 7(8): 1253-1264.
[4] 董艳秋, 韩光. 起重船吊物系统在波浪中的动力响应[J]. 中国造船, 1993, (1): 63-71.
[5] 杜航, 唐力, 尚建忠. 基于动力学分析的机械臂可达性方法研究[J]. 图学学报, 2014, 35(2): 221-225.
[6] 刘金涛. 抓管机工作装置设计关键技术研究[D]. 石家庄: 石家庄铁道大学, 2014.
[7] 李浩东. 吊管机工作装置的多刚体动力学仿真研究[D]. 天津: 河北工业大学, 2003.
[8] 高文杰, 张具安, 曹德本, 等. 吊管机吊臂结构有限元优化及研究[J]. 机械工程与自动化, 2015, (1): 39-41.
[9] 吕宏松. 起重船吊物系统动态特性分析及模型实验研究[D]. 武汉: 华中科技大学, 2009.
[10] 范元勋, 卜廷春, 李水水, 等. 基于 ADAMS/MATLAB的桥式起重机起升动载荷的联合仿真[J]. 重型机械, 2011, (5): 30-32.
[11] 王金刚, 曾刚平, 李浩东, 等. 吊管机配重装置动力学仿真与优化设计[J]. 起重运输机械, 2009, (7): 19-21.
[12] 张建超, 王军, 李义强. 吊管机翻车保护结构的有限元分析与实验研究[J]. 图学学报, 2014, 35(6): 941-945.
[13] 朱会文, 黄启梁, 王宗彦, 等. 机械装备金属结构有限元建模策略研究与应用[J]. 图学学报, 2013, 34(5): 144-147.
Analysis of Dynamic Characteristic of a Pipelayer Crane System Based on MATLAB
Song Qiuhong1,Wang Haohui1,Xu Shaorong1,Yang Shaojie2
(1. College of Engineering, Shanghai Ocean University, Shanghai 201306, China; 2. Shanghai PengPu Machinery Co. Ltd, Shanghai 200072, China)
Pipelayer is a kind of engineering machinery, which is used in the pipe laying and lifting operation, and it would create a dangerous swing sharply under the external incentives. This can not only reduce the lifting precision, but also cause collisions between hanging objects and structures. So it has great importance for safety of pipelayer operation to analysis its system dynamic characteristic, control and predict shimmy. First the article describes the working environment of pipelayer, then proposes summary and comparison of relevant research of domestic and foreign. In this paper, the mathematical model of hanging objects is established, and MATLAB is used to do data analysis. The result shows that length of the sling, external excitation, landing speedcan lead to a great impact on the dynamic response, shimmy frequency and angel of inner and outer surfaces.
pipelayer; nonlinear equations; dynamic analysis; MATLAB
TB 24
10.11996/JG.j.2095-302X.2016010130
A
2095-302X(2016)01-0130-09
2015-07-17;定稿日期:2015-09-22
上海市2014年联盟计划(LM2014013)
宋秋红(1962–),男,吉林长春人,副教授,硕士,硕士生导师。主要研究方向为工程力学、动力工程。E-mail:qhsong@shou.edu.cn

