双船浮吊系统在不规则波作用下动力响应研究

毛垚飞，朱克强*，荆 彪，夏斯琼，许国春

（1.宁波大学海运学院，宁波315211；2.宁波东方电缆股份有限公司，宁波315801）

双船浮吊系统在不规则波作用下动力响应研究

毛垚飞1，朱克强*1，荆 彪2，夏斯琼1，许国春1

（1.宁波大学海运学院，宁波315211；2.宁波东方电缆股份有限公司，宁波315801）

基于起重船在风、浪、流等载荷作用下会引起吊物的大幅度摆动，通过建立吊物系统的动力学模型分析浮吊系统在不规则波作用下的运动响应，研究波高、波向、吊放速度以及波长与船长之比等因素对吊物摆角与吊索张力的影响。得到的结论可用于吊物系统摆动的预测与控制，可供设计者参考。

浮吊系统；不规则波；吊物摆动；动态响应

深海浮吊即起重船，是海上油气开发、海上风机发电、以及各种海上建筑物建造和安装不可缺少的工具。在海洋载荷作用下，船上起重机和吊物产生大幅度摆动，给起吊操作带来危险，同时也会降低吊装精度而埋下安全隐患。尤其是处于恶劣海况下时，吊机在波浪作用下的动力响应状态将急剧恶化。因此研究起重船-吊物系统在波流作用下的动态特性，分析吊物在波浪作用下的摆动特性，对保证浮吊在海上安全作业具有重要意义。

起重船在海上作业时，船体因受到不规则波作用而发生的运动与吊物运动相互耦合，使得研究起吊系统的动力问题复杂化。Henry［1］等构建了一个由无质量吊索和集中质点组成的平面单摆模型，对吊物的摆动进行研究。Witz［2］考虑了吊物系统与船体的耦合效应，分析起吊负载的参数激励对浮吊系统动力响应的影响。Cha［3］等基于多体系统动力学建立了浮吊系统三维非线性运动模型，对浮吊系统在海浪作用下进行动态仿真研究。Lee［4］等通过考虑静水压力的非线性效应对浮吊系统动态响应进行研究，仿真结果表明弹性吊杆对系统动态响应不可忽略。董艳秋［5］研究了起重船在波浪中作业时吊物系统的动力响应，采用新切片理论在频域内得到船体运动，数值计算出吊物摆动规律与吊索动张力。李跃［6］等利用多体力学的休斯顿法，计算了各种工况下吊物的运动轨迹。此外，国内还有很多研究人员对浮吊系统的动力响应进行深入研究［7-8］，得到研究成果对起重船设计与操作给予一定指导。

本文结合前人的研究成果，以海上起重船的吊放作业为背景，重点讨论了不规则波对吊物系统在吊放过程中动态特性的影响。采用时域分析软件OrcaFlex数值模拟吊物入水前后这一过程的动态实时响应与吊索张力的变化时程，以海上双起重船为例，分析波浪要素与吊放速度等因素对吊物摆动与吊索张力的影响，得到的结论对浮吊系统的实际操作具有借鉴意义。

图1 浮吊系统模型图Fig.1 Model diagram of floating crane system

1 浮吊系统基本力学理论

Todd［8］实验研究表明船上吊物系统表现出空间球摆动态行为，表现出混沌和非平面动力响应。本文研究的浮吊系统由双起重船、起重吊杆、吊索以及吊物组成，系统模型如图1所示。文中假定（1）忽略船体与起重吊杆的弹性；（2）吊索的质量相对于吊体与船体的质量小很多；（3）吊索刚度足够大，忽略其弹性变形。

起重船原点O设在静水面上，船体在静水中受到不规则波浪作用后，可产生围绕其原始平衡位置作六个自由度的摇荡运动，且各自由度之间会相互耦合。假定船体运动已知，可写为

式中：x为船体位移（横荡、纵荡、垂荡、横摇、纵摇、艏摇）；a为波浪幅值；ω为波浪频率；R，φ为船体响应幅值算子（RAO）与相位角。

起重吊物在空间摆动，其位置坐标可由垂直面内摆角α与水平面内摆角β来描述，如图2所示。起重船的吊杆端点A与吊体重心Q在惯性坐标系中位置用（xA，yA，zA）和（xQ，yQ，zQ）表示，点A与点Q之间的距离为l，它们之间几何关系为

吊物在下降过程中，竖直面内摆角α随吊索长度增加而发生变化。运用OrcaFlex可计算吊物与吊杆端点A在每个时刻的运动位置，它们可通过相应坐标值来表示，设为（xQi，yQi，zQi）和（xAi，yAi，zAi）。故竖直摆角α计算式可写为

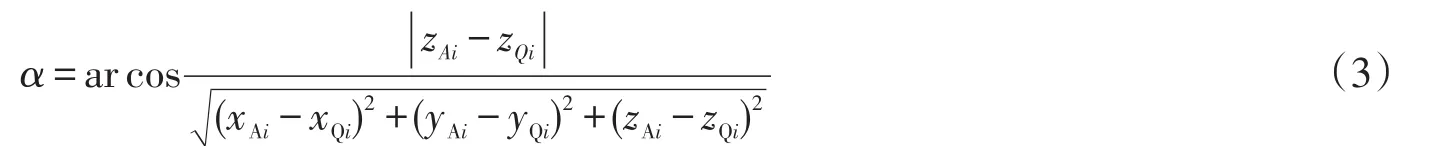
图2 浮吊系统坐标系Fig.2 Coordinate system of floating crane

吊物在下降过程中除了受到吊索的张力外，还会受到海流的作用。吊物不仅将围绕吊索的铰接点产生横摇、纵摇运动，同时也会因吊索产生扭矩而发生艏摇运动，本文将吊体视为六个自由度刚体的运动。

根据牛顿第二定律可建立吊物的矢量运动方程为

式中：R=（xQ，yQ，zQ）；G、B分别为吊物受到重力与浮力；T为吊索的张力，与绳索长度变化有关，其计算表达式［9］

式中：L与L0为吊索的总长与吊放长度；EI为吊索的刚度；ζ为吊索阻尼系数；水动力Fd由惯性力与拖曳力组成，依据莫里森经验公式，可以将其写为

式中：Δ为吊物排水质量；ρ为海水密度；Ca、Cd为吊物附加质量系数与阻力系数；aw、ar为绝对加速度与相对加速度；A为吊物受阻面积。vr为吊物的相对速度，可表示为vr=vc-v0，vr、v0分别为流速与吊物的绝对速度。将吊物的受力投影到x、y、z轴各个方向上，则（4）可以表示为

通过（1）～（7），可求得吊索张力，吊物摆角等动态响应数值（吊物自身的运动过程没有模拟，可能会影响计算结果）。

2 浮吊系统模型建立

2.1 浮吊系统基本结构参数

该浮吊系统由双起重船、起重吊杆、吊索及吊物组成。其中船长为110 m，吃水3.75 m，船体排水量为18 200 t，吊杆长为130 m，船体最大起吊高度为110 m，两船体间距为50 m。吊物距离水面的初始高度为15 m，入水深度为75 m，吊物系统的详细参数见表1。

表1 吊物系统主要参数Tab.1 Main parameters of hanging system

2.2 环境参数

实际海洋中的波浪运动极不规则，不仅表现在波面形状、波浪特性变化，而且还反应在波浪进行传播同时向两边扩散。本文主要研究随机波对浮吊系统影响，采用的波浪为JONSWAP海浪。定义波浪传播方向与X轴之间夹角θ称为波向角，若θ=0°，波浪称为顺浪；θ=90°，波浪称为横浪；θ为其他角度，波浪为斜浪。JONSWAP波谱定义为

式中：S（ω）为谱密度函数；aω为能量尺度因子；g为重力加速度；ω，ωm为波浪频率与波普峰值频率；γ为谱峰升高因子，这里取0.9；σ为峰形参数，其定义为

σ具体赋值可见Isherwood［11］。文中采用的海浪参数见表2，不同水深下海流流速分布如图3。利用OrcaFlex数值软件建立浮吊系统动态模型，研究吊物系统在随机波作用下的动态响应特性。

图3 不同水深下流速分布图Fig.3 Current velocity distribution in different water depth

表2 波浪参数Tab.2 Wave parameters of JONSWAP

3 数值仿真分析

以18 200 t起重船为实例，计算起重船下降作业过程中吊物摆动及吊索张力，分析吊物入水前与入水后的动力响应，研究波浪要素（波高H、波向以及波长与船长比值λ/L）和吊放速度v对浮吊系统动态响应的影响。这里分别记与吊物相连的吊索1与吊索2摆角为α1与α2，吊索张力为T1与T2；取计算模拟时间为110 s，观察吊物系统的动态变化规律。

3.1 浮吊系统本身的动力响应

取吊物下降速度为1 m/s，波浪与船舶纵轴线夹角为90°。把船体设置静止不动，即将浮吊工程船体视为固定的陆基建筑。仅研究了吊物入水前、后环境载荷对其自身的影响。

图4 吊物入水前后摆角α1的响应Fig.4 Response of pivot angleα1before and after hanging objects entering into water

图5 吊物入水前后摆角α2的响应Fig.5 Response of pivot angleα2before and after hanging objects entering into water

图6 吊物入水前后吊索1张力Fig.6 Tension of sling 1 before and after hanging objects entering into water

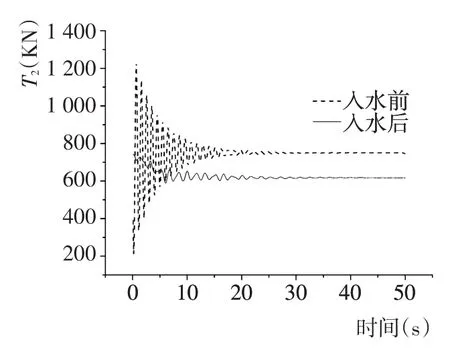
图7 吊物入水前后吊索2张力Fig.7 Tension of sling 2 before and after hanging objects entering into water

由上图可知，由于将船体设置为陆基建筑物，所以在入水前的50 s内没有船体摆动影响，故其摆角α1、α2较小，入水后由于有波流作用的影响摆角变大。入水前张力大于入水后张力，这是由于入水前吊索直接承受吊物重，而入水后由于水对吊物的浮力作用使得其张力减小。

3.2 吊物入水前后对浮吊系统动力响应的影响

取吊物下降速度为0.3 m/s，波浪与船舶纵轴线夹角为90°，吊物入水前距离水面的高度为30 m，吊物入水后下降了35 m的深度，分析吊物入水前后这一过程中的吊物系统动态响应，计算结果如图8～图11。

由上图可知，吊物在入水前后这一过程中，吊物摆角与吊索张力有着明显变化。吊物入水前的数值摆角和吊索张力均大于入水后的响应数值。吊物在空中摆动不会受到海流水动力影响，由于缆长的变化导致了吊物摆动频率的变化，当吊物摆动频率接近于船体受到的外界激励频率时，吊物系统会发生共振现象［7］，此时吊索张力会达到最大，之后吊物摆动频率远离外界激励频率，吊索张力会变小，结果如图6和图7所示。若吊物沉入水中，吊物将受到浮力、流体阻力等水动力外力，这些力将部分抵消重力作用，使得吊物摆角与吊索张力大大减小。

3.3 波高H对浮吊系统动力响应的影响

吊索初始长度l0=15 m，吊物下降的速度v=0.75 m/s，波浪方向为90°，有义波高分别H=0.5 m与H=1 m，吊物摆角及吊索张力如图12～图15所示。

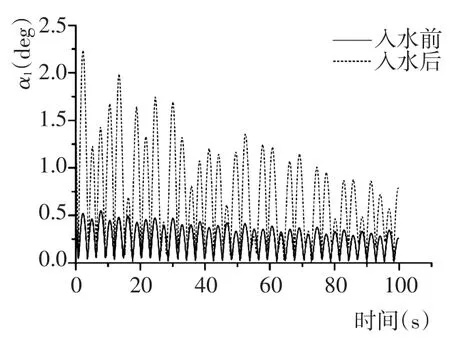
图8 吊物入水前后摆角α1的响应Fig.8 Response of pivot angleα1before and after hanging objects entering into water

图9 吊物入水前后摆角α2的响应Fig.9 Response of pivot angleα2before and after hanging objects entering into water

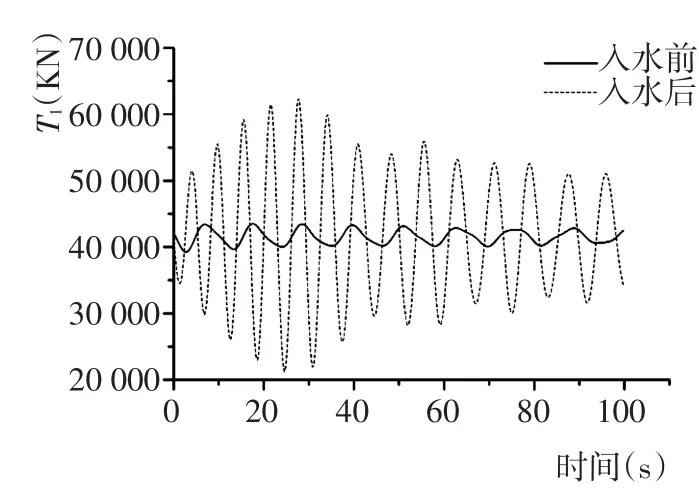
图10 吊物入水前后吊索1张力Fig.10 Tension of sling 1 before and after hanging objects entering into water

图11 吊物入水前后吊索2张力Fig.11 Tension of sling 2 before and after hanging objects entering into water

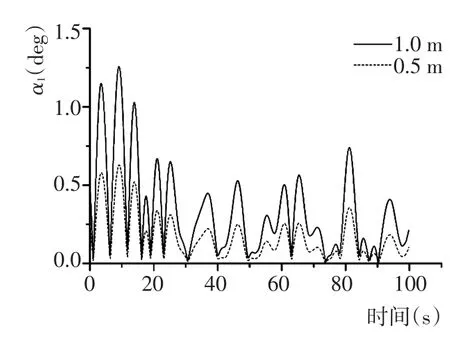
图12 不同波高下摆角α1的响应Fig.12 Response of pivot angleα1in different wave height

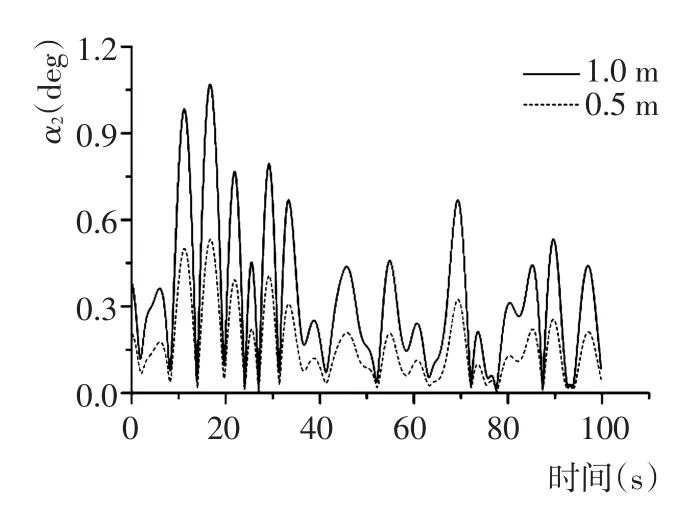
图13 不同波高下摆角α2的响应Fig.13 Response of pivot angleα2in different wave height

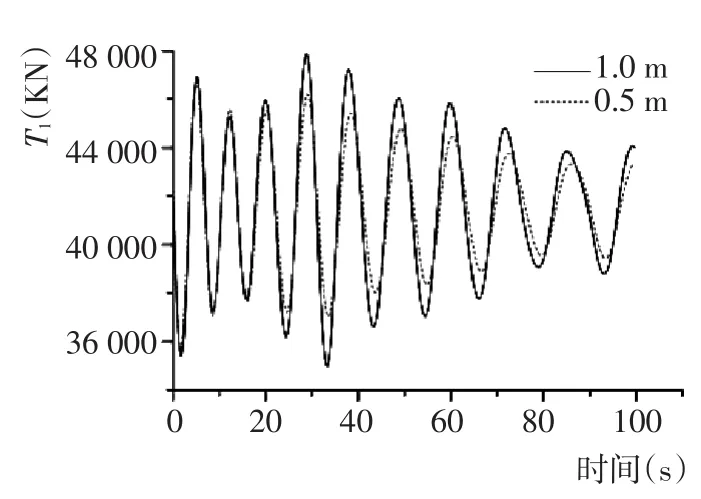
图14 不同波高下吊索1张力Fig.14 Tension of sling 1 in different wave height

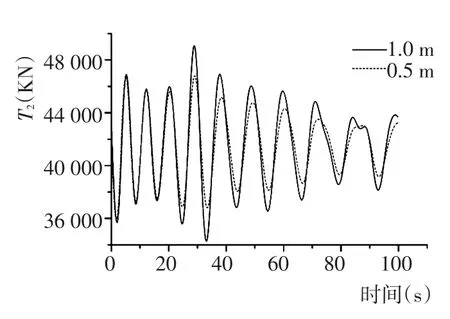
图15 不同波高下吊索2张力Fig.15 Tension of sling 2 in different wave height

从图12～图15可知，波高对浮吊系统的运动影响显著。随着波高的增加，吊物竖直摆角α1、α2增大。当波高不变时，吊物在下降过程中竖直摆角会减小，该现象可解释为吊物在下降过程中，吊索长度不断增加，吊索受到流体水阻力逐渐变大，竖直摆角在缆索阻尼作用下逐步减小。由图10和图11可以看出，初始阶段0～20 s内，吊物还未沉入水中，吊索张力几乎不变。在吊物浸入水中后，吊索张力随着波高的增加而增大，波高对张力有明显影响。

3.4 波向θ对浮吊系统动力响应的影响

其他参数不变，吊物下降的速度v=0.75 m/s，波浪方向θ=0°，45°，90°，吊物摆角及吊索张力如图16～图19所示。

图16 不同波向下摆角α1的响应Fig.16 Response of pivot angleα1in different wave direction

图17 不同波向下摆角α2的响应Fig.17 Response of pivot angleα2in different wave direction

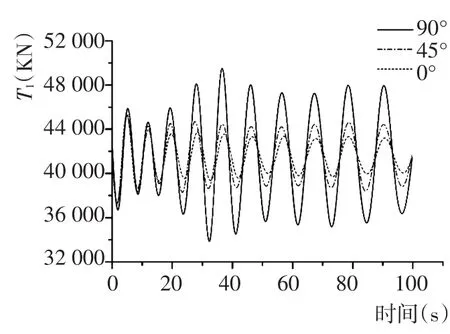
图18 不同波向下吊索1张力Fig.18 Tension of sling 1 in different wave direction

图19 不同波向下吊索2张力Fig.19 Tension of sling 2 in different wave direction

由图16～图19可见，从吊物竖直摆角α1、α2的变化规律来看，横浪作用下吊物的数值摆角最大，顺浪作用下数值摆角最小。结合表3分析波向度吊索张力的影响，可以发现吊索张力也随波浪角的增加而增大，即横浪作用下的吊索张力均大于顺浪及斜浪作用下的张力。故在实际工程安装过程中，要合理调节船体的方位，尽量使船体处于顺浪状态，减小吊物摆动。

3.5 吊放速度v对浮吊系统动力响应的影响

其他参数不变，吊物下降速度v=0.5 m/s，0.75 m/s，1.0 m/s。吊物摆角及吊索张力如图20～图23所示。

由上图看出，吊物吊放作业过程中，随着吊放速度v增大，吊物竖直摆角α1、α2逐渐减小，表明吊放过程速度增大对吊物摆动具有抑制作用；反之，吊索张力随吊放速度增加而增大，如图20～图23所示。这是因为吊物下降速度的增加引起吊索附加动载荷增大，同时吊索长度增加使得作用在吊索上的水阻力增大，故吊索张力变大。故在实际工程应用中应合理控制吊放速度的大小，不仅要确保吊物运动的稳定性，且要避免因吊速过大导致吊索发生损坏。

表3 波向对吊索最大张力影响Tab.3 Response of the maximum tension with different wave direction

3.6 波长与船长比值λ/L对浮吊系统动力响应的影响

首先分析λ/L对吊物最大竖直摆角α的影响，其次分析吊索最大张力Tmax随λ/L的变化规律。取λ/L=0.2，0.4，···2.6，波向θ=0°，45°，90°，计算结果如图20～图21所示。

从图24可见，不同波向下的吊物最大竖直摆角αmax先随着λ/L的增加而增大，之后αmax随λ/L的增加而缓慢减小，其变化幅值很小。三种波向下的最大摆角αmax值均在λ/L=1.2时取得，由图中可看出，横浪作用下的数值摆角最大，为5.92°。以上现象表明，在波高一定时，船体在波浪上的运动响应与波长有直接关系，波长通过影响船体的运动间接影响吊物系统运动。当波长的幅值与船长相近时，吊物摆动角度达到最大，此情况下吊物运动剧烈，易产生危险事故。

从图25可见，不同的λ/L比值对吊索的最大张力影响不同。横浪作用下吊索张力极值高于顺浪以及斜浪作用下的张力极值，该工况下张力极值为61 114.4 KN，对应的λ/L比值为1.4。由图中可知，在λ/L比值达到2.0后，如表三所示，波向对吊索最大张力有较小影响。以上结果表明，横浪作用下的吊索张力最大，且当波长为船长1.4倍时，吊索最大张力达到极值。若波长大于两倍船长，吊索最大张力受波向影响很小，其稳定在某一定值。故在实际海况中，要控制好船体运动方向，使得吊索最大张力降为最低。

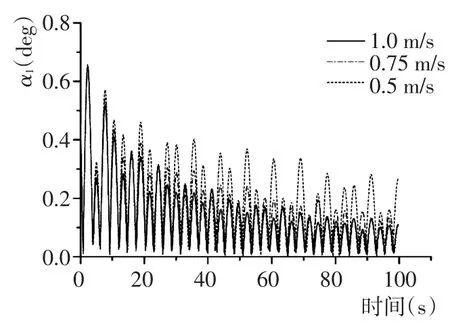
图20 不同吊速下摆角α1的响应Fig.20 Response of pivot angleα1in different falling velocity

图21 不同吊速下摆角α2的响应Fig.21 Response of pivot angleα2in different falling velocity

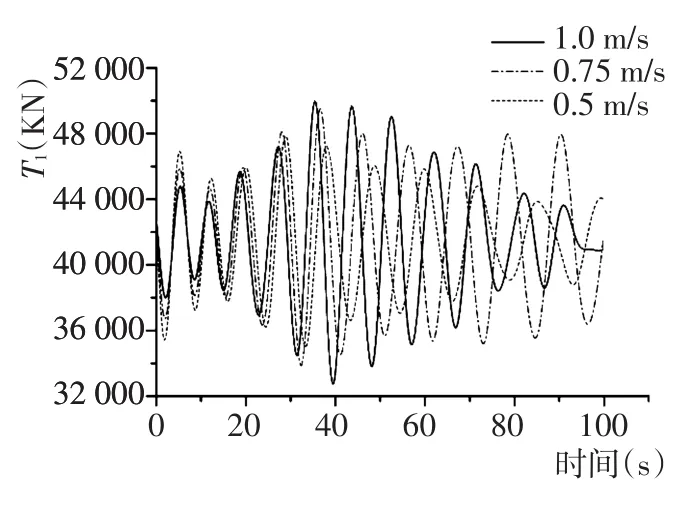
图22 不同吊速下吊索1张力Fig.22 Tension of sling 1 in different falling velocity

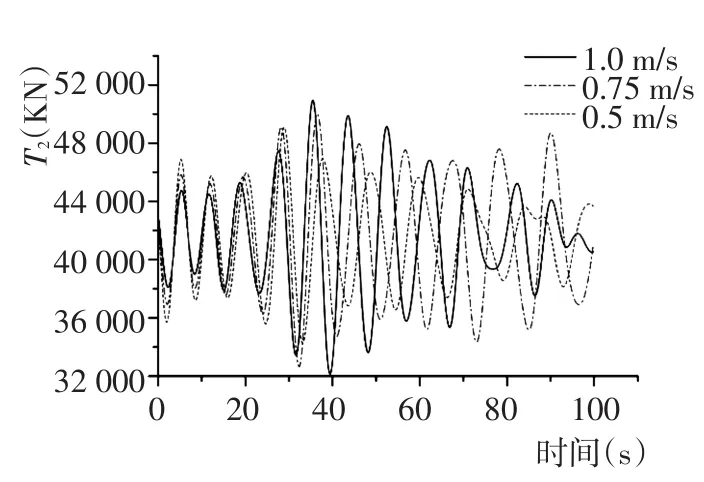
图23 不同吊速下吊索2张力Fig.23 Tension of sling 2 in different falling velocity

图24 波长比对最大摆角α影响Fig.24 Response of the maximum pivot angleαwith differentλ/L

图25 波长比对吊索最大张力影响Fig.25 Response of the maximum tension with differentλ/L

4 结语

本文建立了海上作业浮吊系统三维非线性运动模型，重点讨论了起重船吊放作业时吊物的摆动响应和吊索的有效张力变化。采用数值计算软件OrcaFlex对随机波作用下系统的动态响应进行了仿真研究，相关分析结论如下所示。

（1）吊物系统入水前的动态响应比入水后的动态响应剧烈，吊物在空中摆动不会受到海流水动力影响，由于缆长的变化导致了吊物摆动频率的变化，当吊物摆动频率接近于船体受到的外界激励频率时，吊物系统会发生共振现象，此时吊索张力会达到最大，之后吊物摆动频率远离外界激励频率，吊索张力会变小。

（2）起重船在横浪中作业时，吊物竖直摆角α与吊索张力均随波高的增加而增大，吊物在下放过程中竖直摆动趋势会逐渐减弱，波高对竖直摆动角的影响降低。

（3）当船体与波浪夹角为90°时，吊索张力与吊物摆角达到最大，此时浮吊系统的动态响应最为剧烈。故在实际工程安装过程中，要合理调节船体的方位，尽量使船体处于顺浪状态，减小吊物摆动。

（4）吊物在下降过程中，吊放速度越大，吊物竖直摆角α越小，而吊索张力随下降速度增加会逐步增大。从抑制吊物摆动的目的出发虽然增大吊放速度具有优势但由此照成的吊索张力增大将产生巨大安全隐患，因此吊物的下降速度不宜过大。

（5）波长与船长比值（λ/L）对系统的动态响应具有显著影响。当波长的幅值与船长相近（λ/L=1.2）时，横向波作用下的吊物摆角达到最大；若波长幅值λ为船长1.4倍，则吊索张力达到极值。当λ/L比值大于2时，吊索最大张力受波向的影响较弱。

通过对浮吊系统仿真结果的研究可以发现，影响起重船吊放作业动态响应的因素比较复杂，这些因素必须在起重船操作过程中认真考虑，避免起重船吊装作业发生安全事故。

参考文献：

［1］Henry R J，Masoud Z N.Cargo Pendulation Reduction of Ship-Mounted Cranes Via Boom-Luff Angle Actuation［J］.Journal of Vibration and Control，2001，7（8）：1 253-1 264.

［2］Witz J A.Parametric Excitation of Crane Loads in Moderate Sea States［J］.Ocean Engineering，1995，22（4）：411-420.

［3］Ju-Hwan Cha.Dynamic response simulation of a heavy cargo suspended by a floating crane based on multibody system dynamics［J］.Ocean Engineering，2010，37：1 273-1 291.

［4］Lee K Y，Cha J H，Park K P.Dynamic response of a floating crane in wave by considering the nonlinear effect of hydrostatic force［J］.Ship Technology Research，2010，57（1）：62-71.

［5］董艳秋，韩光.起重船吊物系统在波浪中的动力响应［J］.中国造船，1993，120（1）：63-71. DONG Y Q，HAN G.Dynamic response of lifting load system of crane vessel in waves［J］Shipbuilding of China，1993，120（1）：63-71.

［6］李跃，沈庆，陈徐均.波浪环境中作业起重船悬吊载荷的摆振分析［J］.建筑机械，2003（8）：55-61. LI Y，SHEN Q，CHEN X J.Swing analysis of suspended load of crane ship on the wave［J］.Construction Machinery，2003（8）：55-61.

［7］任会礼，王学林，胡于进，等.起重船吊物系统动力响应仿真分析［J］.系统仿真学报，2007，12（19）：2 665-2 668. REN H L，WANG X L，HU Y J，et al.Dynamic Response Simulation of Lifting Load System of Ship-mounted Cranes［J］.Journal of System Simulation，2007，12（19）：2 665-2 668.

［8］荆彪，朱克强，张天宇.起吊系统在规则波作用下动态仿真分析［J］.水道港口，2015（5）：398-403. JING B，ZHU K Q,ZHANG T Y.Dynamic simulation analysis of floating crane system in regular waves［J］.Journal of waterway and harbor，2015（5）：398-403.

［9］Todd M D,Vohra S T,Leban F.Dynamical measurements of ship crane load pendulation［C］//Hugh Macpherson.OCEANS'97

MTS/IEEE Conference Proceedings.Halifax：oceans′97 mts/ieee conference committee,1997：1 230-1 236.

［10］Orcina.OrcaFlex manual［EB/OL］［2015-6-4］.http：//www.orcina.com/SoftwareProducts/OrcaFlex/Validation/index/.pdf.

［11］Isherwood R M.A Revised Parameterization of the JONSWAP Spectrum［J］.Applied Ocean Research，1987，1（9）：47-50.

Dynamic response analysis of two boat floating crane system in irregular waves

MAO Yao-fei1,ZHU Ke-qiang*1,JING Biao2，XIA Si-qiong1,XU Guo-chun1
（1.Faculty of Maritime and Transportation,Ningbo University,Ningbo315211,China;2.Ningbo Orient Wires& Cables Co.,Ltd.,Ningbo315801,China）

Because the random wave induced motion of floating crane can produce substantial swing of the hanging cargo,a dynamic model of hoisting system was established in this paper.The dynamic response of floating crane system in the irregular waves was analyzed.The influences of wave height,wave direction,dipping speed and the ratio of length between wave and hull on swing angle and sling tension were demonstrated.Conclusion obtained from this paper can be used for cargo swing prediction and manipulation,as a reference for the designers.

floating crane system;irregular wave;cargo swing;dynamic response

U 661.73；U 651

A

1005-8443（2017）01-0031-07

2016-05-03；

2016-06-25

国家自然科学基金资助项目（11272160）

毛垚飞（1991-），男，江西上饶人，硕士研究生，主要从事船舶与海洋工程结构动态响应研究。

*通讯作者：朱克强，教授，博导，主要研究船舶与海洋工程结构动态响应。E-mail：zhukeqiang@nbu.edu.cn.

Biography：MAO Yao-fe（i1991-），male，master student.