波浪与直墙前多层透空薄板作用的解析研究

耿宝磊，王荣泉，宁德志，张慈珩，赵 鹏

（1.交通运输部天津水运工程科学研究所港口水工建筑技术国家工程实验室工程泥沙交通行业重点实验室，天津300456；2.大连理工大学海岸与近海工程国家重点实验室，大连116024）

波浪与直墙前多层透空薄板作用的解析研究

耿宝磊1，王荣泉2，宁德志2，张慈珩1，赵 鹏1

（1.交通运输部天津水运工程科学研究所港口水工建筑技术国家工程实验室工程泥沙交通行业重点实验室，天津300456；2.大连理工大学海岸与近海工程国家重点实验室，大连116024）

文章基于势流理论下均匀透空薄板内部流体连续方程和忽略对流项的欧拉方程，得到薄板内流体水平速度与压力差间的关系，进而建立了波浪与直墙前单层和多层透空薄板作用模型，通过匹配薄板两侧的边界条件，可求得直墙前透空薄板对波浪的反射系数、透射系数以及波能的吸收率。算例针对水深2.5 m，入射波浪周期3.5 s的工况，研究了直墙前12 m范围内设置不同层数透空薄板时，反射系数、透射系数及波能吸收率随组合参数G的变化，结果表明当布置四层透空薄板且0.8＜Gr＜4.6、0＜Gi＜1.6时，本算例波浪的吸收率可达90%以上。

波浪；多层透空薄板；吸收率；反射系数；透射系数

开孔直立结构具有消能效果好、波压力小等优点，在直立码头、防波堤、水槽消波等实际工程中得到了广泛应用。国内外很多学者对波浪与开孔结构作用进行了很多研究。在试验研究方面，杜金曼和吴承元［1］研究了多层直立消波装置的反射系数和透射系数的影响因素。戴冠英［2］、张芹和戴冠英［3］开展模型实验研究了开孔率较小时（0.15＜ε＜0.25）直立全开孔板或全开孔板后带实体墙两种结构形式的波浪反射系数及结构所受的波压力变化规律，并给出了反射系数、透射系数及波压力与结构形式、水深、波要素之间的回归关系式。马宝联等［4］和Tanimoto等［5］分别针对开孔沉箱结构进行了试验研究，分析了反射系数与消浪室相对宽度和开孔率等影响因素之间的关系。

在理论研究与数值分析方面，Yu［6］基于线性势流理论研究了波浪对透水半无限防波堤的绕射作用。Chwang和Chan［7］基于达西定律分析了波浪与透空结构的作用，分析了透空结构对减小港内波浪和港内共振的影响。Twu和Lin［8］等采用解析的方法研究了多块透空板不同布置间距对波浪的反射的影响，并发现前面板的开孔率较大，后面板开孔率较小对波浪有较好的吸收效果。李世森等［9］在波浪数值水槽模型末端采用沿水槽纵轴方向具有渐变垂向孔隙率的孔隙结构消除反射波，并分析了不同因素对消波性能的影响。陈雪峰等［10］利用数值水槽对波浪与开孔板作用进行了数值分析，研究了开孔率等因素对开孔板点压力分布和反射系数的影响。

本文基于势流理论，建立了波浪与直墙前多层透空薄板作用的数学模型，利用解析方法得到了多层透空薄板对波浪的反射系数、透射系数及波能的吸收率，进一步通过具体算例分析了组合参数G对透空薄板消波性能的影响。

1 透空薄板内流体运动控制方程

图1为单层透空薄板示意图，模型采用势流理论，在均匀薄板内部流体流动满足连续方程和忽略对流项的欧拉方程如下［11］：

式中：U为流体的速度矢量；r为流体密度；P为流体压强，t为时间；f为薄板的阻力系数；w为入射波浪频率；Cm为附加质量；e为薄板开孔率。

对于速度U和压强P，按下式分离出时间因子

可得其复变量u和p的方程为

式中

其实部和虚部分别对应介质的阻力和惯性影响。

假设薄壁只横向透水，忽略掉流体的垂向分量，可得到薄板内水平速度与压力差间的关系为

式中b为薄板的厚度，下标0和b分别表示薄板两侧的物理量。

将孔隙中的流速换算成整个板上的流速，并与外部波动速度相匹配，得

通过对不同情况下速度势与边界条件的匹配，可以得出直墙前单层和多层透空薄板模型对波浪的反射系数、透射系数以及波浪能量损失的表达式。

图1 透空薄板模型示意图Fig.1 Sketch of grid plate model

图2 波浪与直墙前单层透空薄板作用Fig.2 Wave action with one grid plate in front of wall

2 波浪与直墙前单层透空薄板作用

对于图2所示的波浪与直墙前单层透空薄板的作用问题，在W1和W2区域内，速度势f1和f2应满足以下条件：

自由水面条件

式中g为重力加速度。

水底条件

无穷远条件

式中φ0为入射势，k为波数，i为虚数单位。

直墙上物面条件

根据式（8）和式（9），并令

其中，实部Gr主要跟介质引起的阻力系数有关，虚部Gi主要跟透空介质引起的附加质量系数有关。式（9）可写为

忽略透空薄板的厚度，在薄板处的速度连续条件可写为

对于匹配条件式（15）和式（16），φ1和φ2中不包括非传播项［6］，这样φ1和φ2可写为

式中A为波幅；h为水深；R和T为待定系数。将φ1和φ2代入（13）、（14）式可解得

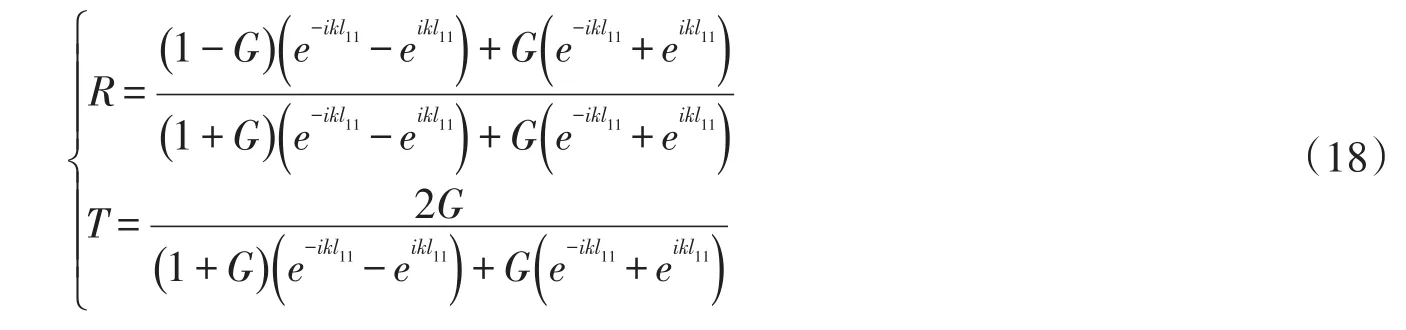
则单层透空薄板的反射系数Kr和透射系数Kt分别为

波浪穿过单层透空薄板的能量损失系数为

将波浪与直墙前透空薄板作用时的能量损失和透射波浪作为入射波浪的消减部分，则透空薄板对波能的吸收率定义为

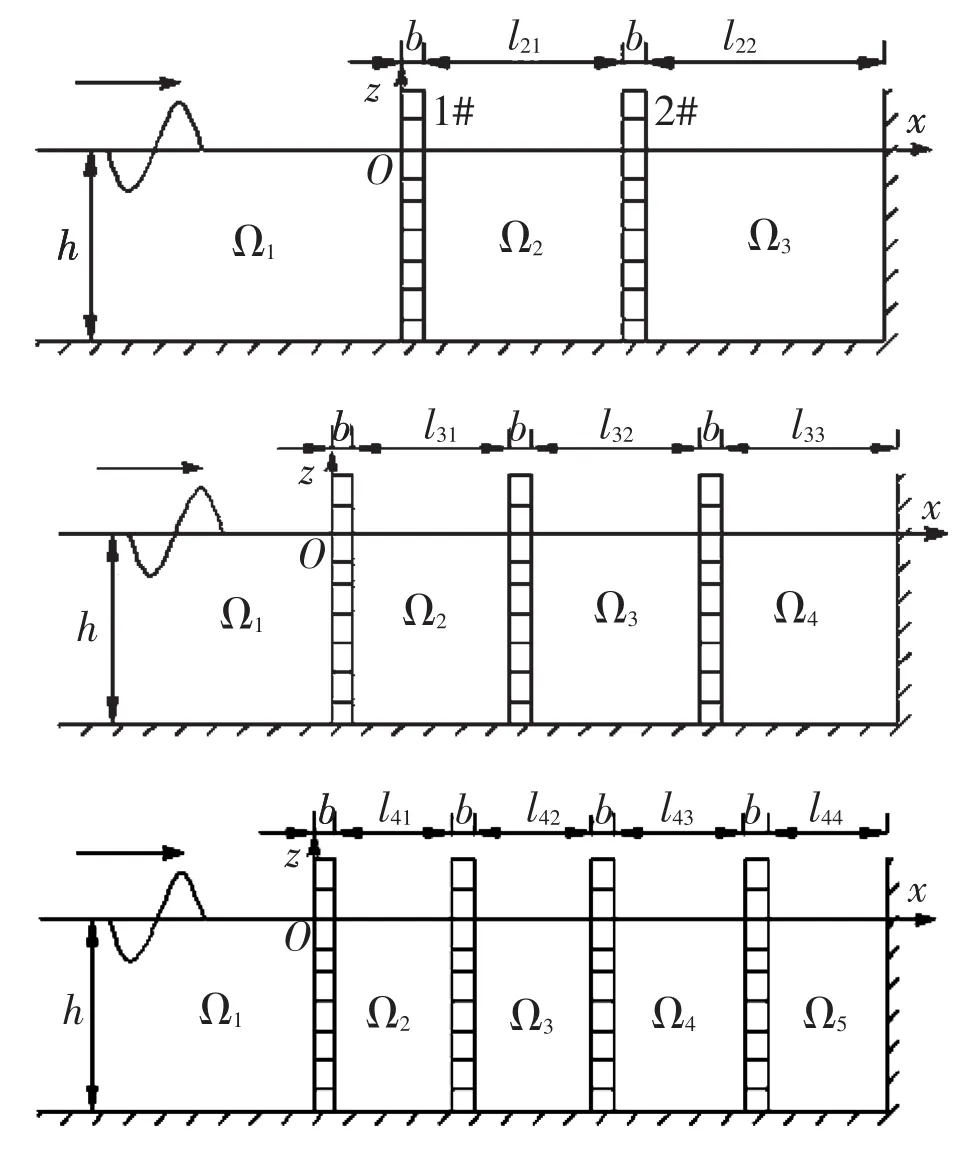
图3 波浪与直墙前多层透空薄板作用示意图Fig.3 Wave action with multi-layer perforated plates in front of the wall

3 波浪与直墙前多层透空薄板作用

按照同样的方法可以求得波浪与直墙前多层透空薄板作用的情况，图3是波浪与直墙前两层、三层和四层透空薄板作用的示意图。

3.1 波浪与直墙前两层透空薄板作用

以波浪与直墙前两层透空薄板作用为例，两层薄板内水平速度与压力差间的关系分别为

式中：lmn表示薄板的间距，其中m表示栅格层数，n表示第n和n+1层的间距；分别将两层薄板孔隙中的流速换算成整个板上的流速，并与外部波动速度相匹配，得

同样令G=ε/Ωkb=Gr+iGi，（23）式可写为

忽略透空薄板的厚度，则在两层薄板处的速度连续条件可写为

速度势φ1、φ2和φ3的表达式为

式中R1和T1分别表示第一层透空薄板复变量的反射系数和透射系数；R2和T2分别表示第二层透空薄板复变量的反射系数和透射系数。此外，由于不透水直墙对波浪发生全反射，反射系数仍为T2。

将速度势φ1、φ2和φ3代入上述匹配条件式（24）和（25）可求得

式中

由此可得直墙前两层透空薄板对波浪的反射系数Kr和透射系数Kt分别为

直墙前双层透空薄板对波能的吸收率同式（21）。

3.2 波浪与直墙前三层透空薄板作用

波浪与直墙前三层透空薄板作用时，各层薄板复变量的反射系数和透射系数表达式为

3.3 波浪与直墙前四层透空薄板作用

波浪与直墙前四层透空薄板作用时，各层薄板复变量的反射系数和透射系数表达式为

由此可得直墙前四层透空薄板对波浪的反射系数Kr和透射系数Kt分别为

4 算例分析

根据式（7）和（14），可以得到G的表达式为

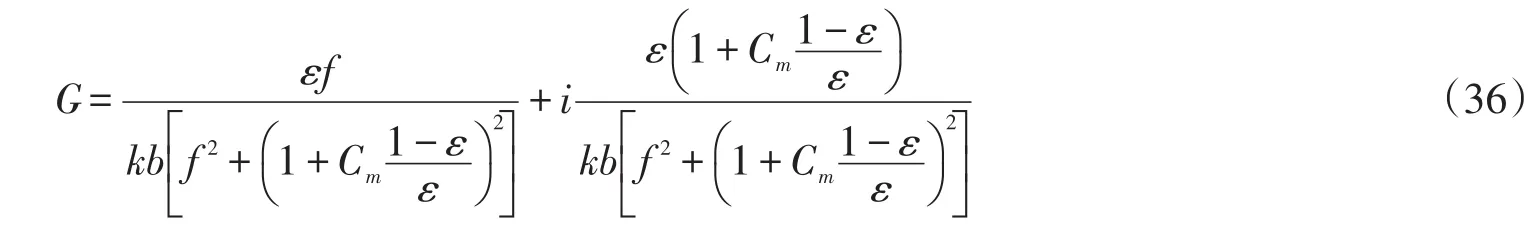
为研究反射系数、透射系数和波能吸收率与G的关系，选取特定的算例进行计算，其中水深h=2.5 m，入射波浪周期为3.5 s，第一层薄板距离直墙的距离为12.0 m。

（1）布置单层透空薄板

布置单层透空薄板时，l11=12.0 m。计算结果见图4。

图4 单层透空薄板的反射系数、透射系数与波能吸收率变化曲线Fig.4 Reflection coefficient,transmission coefficient and absorption rate for one perforated plate

根据式（36），当附加质量Cm取为0时，G的实部Gr和虚部Gi与开孔率ε成正比。根据图4中Kr的变化曲线，当Gr和Gi较小或较大时，反射系数都很大，可以解释为当Gr和Gi较小时，开孔率ε较小，此时透空薄板相当于不透水直墙，故而反射系数很大；而当Gr和Gi较大时，开孔率ε较大，此时大部分波浪能透过透空板，但是，波浪在后面直墙发生全反射进而又透过透空板进入入射波场，相当于透空板发生反射，因此Gr和Gi较大时反射系数也很大。

同理，对于图4中Kt的变化曲线，当Gr和Gi较小时，开孔率ε较小，此时透空薄板相当于不透水直墙，故而透射系数很小；而当Gr和Gi较大时，开孔率ε较大，此时大部分波浪能透过薄板，故透射系数很大。

从图4中Ka的变化曲可以看到，当Gr在0.6～1.6之间取值，Gi在0～0.3之间取值时，能使得波浪能量的吸收率达到90%以上，只是Gr和Gi的有效取值范围较小。

（2）布置双层透空薄板

布置双层透空薄板时，l21=l22=6.0 m，计算结果见图5。从Ka的变化曲线可以看到，当Gr在0.8～2.2之间取值、Gi在0～0.35以内取值时，波浪吸收率能达到90%以上。波浪通过双层薄板后也只在较小的区域能达到好的消波效果，但相对单层薄板的情况略有改善。

（3）布置三层透空薄板

布置三层透空薄板时，l31=l32=l33=4.0 m，计算结果见图6。从Ka的变化曲线可以看到，当Gr在0.7～3.5之间取值、Gi在1.0以内取值时，波浪吸收率能达到90%以上。波浪通过三层薄板后，消波效果相对前两种布置方式有较为明显的改善。

（4）布置四层透空薄板

布置四层透空薄板时，l41=l42=l43=l44=3.0 m，计算结果见图7。从Ka的变化曲线可以看到，当Gr在0.8～4.6之间取值、Gi在1.6以内取值时，波浪吸收率能达到90%以上。波浪通过四层薄板后，消波效果较之前三种情况有明显增强。

通过图4～图7的对比可以发现，随着直墙前透空薄板数量的增加，能使波能吸收率大于90%的Gr和Gi取值范围在不断增加，也就是说，通过增加透空薄板的数量能有效提高系统对波浪的吸收，减小波浪的反射。

图5 双层透空薄板的反射系数、透射系数与波能吸收率变化曲线Fig.5 Reflection coefficient,transmission coefficient and absorption rate for two perforated plates

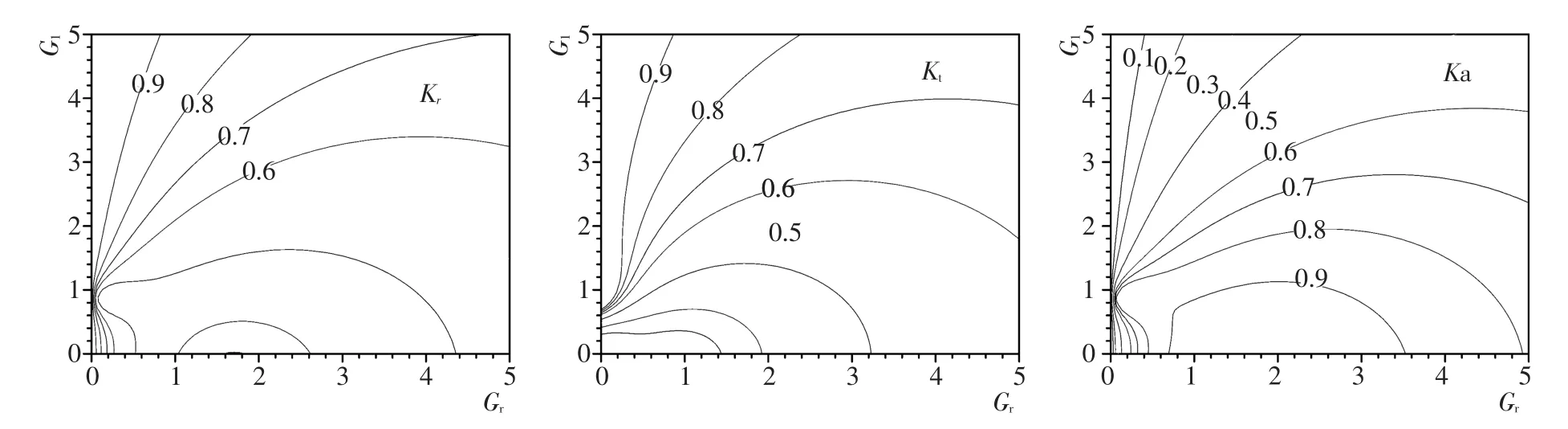
图6 三层透空薄板的反射系数、透射系数与波能吸收率变化曲线Fig.6 Reflection coefficient,transmission coefficient and absorption rate for three perforated plates

图7 四层透空薄板的反射系数、透射系数与波能吸收率变化曲线Fig.7 Reflection coefficient,transmission coefficient and absorption rate for four perforated plates

5 结论

本文基于势流理论建立了波浪与直墙前多层透空薄板作用模型，得到了多层透空薄板装置的反射系数、透射系数以及对波能的吸收率，进一步通过具体算例分析了组合参数G的变化对反射系数、透射系数及吸收率的影响，研究结果表明当0.8＜Gr＜4.6、0＜Gi＜1.6时，本算例波浪的吸收率可达90%以上。

组合参数G包含了薄板的孔隙率、薄板宽度、薄板的阻力系数、附加质量以及入射波浪的波数等，进一步的研究将针对不同参数的变化给出直墙前多层透空薄板装置波能吸收率变化的敏感性，研究成果可为新型消波装置的开发提供借鉴。

参考文献：

［1］杜金曼,吴承元.多层透空直立式消波器［J］.水利水运科学研究,1984（4）：79-88. DU J M,WU C Y.Multi-layer perforated vertical wave absorber［J］.Hydro-Science and Engineering,1984（4）：79-88.

［2］戴冠英.波浪作用下开孔直立结构的反射与透射性能［J］.水利水运科学研究,1993（3）：291-300. DAI G Y.Reflection and transmission performances of vertical perforated structure under wave action［J］.Hydro-Science and Engineering,1993（3）：291-300.

［3］张芹,戴冠英.波浪对开孔直立结构作用力的试验研究［J］.水利水运科学研究,1994（4）：367-374. ZHANG Q,DAI G Y.Experimental study on interaction between waves and vertical perforated structures［J］.Hydro-Science and Engineering,1994（4）：367-374.

［4］马宝联.波浪与开孔直墙式防波堤的相互作用［D］.大连：大连理工大学,2004.

［5］Tanimoto K,Yoshimoto Y.Theoretical and experimental study of reflection coefficient for wave dissipating caisson with a permeable front wall［J］.Report of the Port and Harbour Research Institute,1982,21（3）：44-77.

［6］Yu X.Diffraction of water waves by porous breakwaters［J］.Journal of waterway,port,coastal,and ocean engineering,1995,121（6）：275-282.

［7］Chwang A T,Chan A T.Interaction between porous media and wave motion［J］.Annual Review of Fluid Mechanics,1998,30（1）：53-84.

［8］Twu S W,Lin D T.Wave reflection by a number of thin porous plates fixed in a semi-infinitely long flume［J］.Coastal Engineering Proceedings,1990,1（22）：21-23.

［9］李世森,江鸣.数值波浪水槽末段孔隙结构消波性能的研究［J］.港工技术,2012（49）：1-4. LI S S,JIANG M.Study on Wave-absorbing Performance of Porosity Solid in End-piece of Numerical Wave Flume［J］.Port Engineering Technology,2012（49）：1-4.

［10］陈雪峰,张梅,李玉成.开孔率对开孔板消浪效果影响的数值模拟研究［J］.水道港口,2013（34）：285-292. CHEN X F,ZHANG M,LI Y C.Numerical simulation study on effect of porosity on performance of perforated structures［J］.Journal of Waterway and Harbor,2013（34）：285-292.

［11］李玉成,滕斌.波浪对海上建筑物的作用［M］.北京.海洋出版社出版社，2015.

Analytical study on wave interaction with multi-layer perforated plates in front of vertical wall

GENG Bao-lei1,WANG Rong-quan2,NING De-zhi2,ZHANG Ci-heng1,ZHAO Peng1
（1.Tianjin Research Institute for Water Transport Engineering，National Engineering Laboratory for Port Hydraulic Construction Technology,Key Laboratory of Engineering Sediment,Ministry of Transport,Tianjin300456,China;2. State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian116024,China）

Based on potential flow theory,an analytical study on wave action with one grid plate or multi-grid plates was carried out.Continuity equation and Euler equation without convective term were used to get the relationship between horizontal velocity and pressure difference of the fluid in the thin plate.By matching the boundary conditions at two sides of the plate,reflection coefficient,transmission coefficient and absorption rate were developed. Examples with water depth 2.5 m,incident wave period 3.5 s and wave absorbing distance 12 m were carried out to study the effects of different plates numbers with an assembly parameterG,and the results show that the absorption rate of four-layer perforated plates is bigger than 90%when 0.8＜Gr＜4.6 and 0＜Gi＜1.6.

wave;multi-grid plates;absorption rate;reflection coefficient;transmission coefficient

U 656.2；O 242.1

A

1005-8443（2017）01-0008-08

2016-06-17；

2016-07-27

交通运输部应用基础研究计划项目（2014329224380）；国家自然科学基金（51409135）；天津市应用基础与前沿技术研究计划（15JCQNJC07300）；中央级科研院所基本科研业务费专项（TKS150203）

耿宝磊（1980-），男，河北省衡水人，副研究员，主要从事波浪理论及波浪与结构物作用研究。

Biography：GENG Bao-lei（1980-），male，associate professor.