大型半潜船波浪弯矩间接监测方法研究

崔家林，张金钊，张猛，刘红兵，曲先强

（1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001；2.上海船舶设备研究所，上海 200031；3.哈尔滨工程大学 烟台研究院，山东 烟台 264000）

船体强度在线监测的合理应用可有效提高船体 结构的安全性，其中监测船体梁实际承受的波浪弯矩是船体强度监测的一种方式。基于传统方法的非大开口船型波浪弯矩间接监测系统已经在工程中应用多年，主要通过布置在船中位置处的长基线应变仪监测船体结构的纵向平均应变，然后基于船体梁纯弯曲假定计算出监测横剖面的总纵弯矩和横向弯矩。这种方法的精度需要进一步验证［1］。

结构载荷监测包括直接监测和间接监测。载荷的直接监测或直接测量难度大，对传感器的要求极高，甚至有些载荷无法测量，因而在工程中难以应用。随着载荷识别技术的进步，反求算法精度的提高等，载荷的间接监测可逐步引入工程应用。

结构载荷的间接监测，即载荷识别，是结构力学中的反问题［2］。船舶与海洋工程结构实际遭遇的载荷多种多样，包括局部载荷与总体载荷。由于大型船舶尤其是超大型并伴随有甲板大开口的船舶在波浪中航行时受到的载荷很大且具有很强的随机性，而在设计和建造过程中不可能准确预料这些随机性载荷，甚至有些船舶已经超过了规范的适用范围［3］。因此保证大型船舶的结构和航行安全就显得极为重要。

金永兴等［4］开发了集装箱船船舶结构状态监测和评估系统（container ship structural condition monitoring and evaluation systen,CSSMAS），该系统通过在船体关键位置安装电阻式应变传感器和加速度传感器，在船艏和船尾分别安装波浪图像传感器实现对船体结构安全的监测，系统通过万吨级集装箱船“育峰”轮实船测试。王为等［5］通过对Nishihara 箱型梁模型在中垂状态下的应力、应变分布的有限元力学分析，研究了水面船舶总纵强度监测时的传感器优化布置原则。张猛等［6-8］以板架结构分布式冰载荷、船体梁波浪弯矩及扭矩这3 种典型载荷为例开展研究，建立了一套可靠有效的载荷反演方法，通过监测的结构响应实时给出作用于船舶与海洋工程结构上的3 种典型载荷，为结构安全在线监测提供参考和支撑。Xu等［9］在船体垂荡及纵摇运动与波浪弯矩之间通过神经网络方法建立了完整的映射关系，即通过结构运动数据计算结构实际承受的波浪弯矩。模型试验证明了这种波浪弯矩间接监测方法的准确性。Moreira 等［10］在船体6-自由度运动与垂向波浪弯矩及剪力之间通过神经网络方法建立了完整的映射关系，即通过结构运动数据计算结构实际承受的垂向波浪弯矩及剪力。

本文阐述船体波浪弯矩间接监测传统方法，并基于某大型半潜船的全船有限元仿真验证这种方法的精度。在船体波浪弯矩间接监测传统方法的基础上提出一种稳定且精度较高的船体波浪弯矩间接监测的改进方法，通过C-最优设计法和D-最优设计法优化长基线应变仪的安装位置，并通过全船有限元仿真构建改进方法的数学模型。

1 波浪弯矩间接监测传统方法

在梁弯曲理论中，纵向应变可认为沿厚度方向成线性分布，中和轴处应变为零，如图1所示。于是纵向应变可表示为：

图1 梁弯曲变形Fig.1 Bending deformation of beam

以某大型半潜船为例，其监测横剖面的局部坐标系定义为：坐标系原点在横剖面形心上，Z轴正向向上，Y轴正向指向左舷，X轴正向指向船艏，如图2所示。此外，总纵弯矩能使船体中拱为正，横向弯矩能使船体向左舷拱起为正。

图2 局部坐标系定义Fig.2 Definition of local coordinate system

若在船体结构两位置安装长基线应变仪以监测实际应变，假定传感器安装位置处的结构纵向应变仅由总纵弯矩与横向弯矩引起，且应变不超过材料的比例极限，传感器安装位置点处的应变可以线性叠加表示为：

将其表示为矩阵形式：

式（3）可简化为：

式中：传递矩阵K2×2可根据船体横剖面计算得到，即只需得到结构横剖面惯性矩Iy、Iz和传感器安装位置的坐标即可；应变向量ε2×1可通过结构监测得到。传递矩阵K2×2和应变向量ε2×1得到后，载荷向量M2×1可由直接求逆法得到：

监测横剖面承受的波浪弯矩与船体纵向平均应变间的线性关系仅在以下情况下适用：

1）结构应力在结构材料的比例极限之内，即满足胡克定律；

2）船体仅承受纯弯曲作用。

但在工程应用中，监测横剖面承受的载荷包括波浪弯矩、波浪扭矩、局部波动压力以及货物载荷等。因此，波浪弯矩间接监测的数学模型，即式（3）、（4），只是近似适用，其精度水平需要进一步验证。

波浪弯矩间接监测的传统方法是建立在船体梁纯弯曲假定之上。船体梁在波浪载荷或其他载荷作用下发生的弯曲不可能是纯弯曲，如在垂向或横向剪力作用下船体梁横剖面会产生翘曲。此外，船舶也会发生扭转作用，船体扭转包含圣·维南扭转和二次扭转2种主要成分。二次扭转会引起船体横剖面翘曲。虽然圣·维南扭转不会引起船体横剖面翘曲，但会对长基线应变仪的监测结果造成干扰。总之，将非大开口船型的总体变形仅归因于总纵弯矩和横向弯矩且认为结构纵向应变沿船体横剖面线性分布有其不当之处。

2 波浪弯矩间接监测的改进方法

由于波浪弯矩间接监测的传统方法的计算精度一般，应对波浪弯矩间接监测算法进行改进以获得更高精度的解。本文基于C-最优和D-最优设计法提出了一种混合最优设计法。用C-最优设计法和D-最优设计法优化传感器安装位置，并在此基础上建立数学模型。

波浪弯矩间接监测的改进方法包含2 个主要部分：1）传感器安装位置的优化；2）数学建模。传感器安装位置的优化是为了降低监测误差对计算结果的影响，在此基础上建立的数学模型可以提高反求结果的精度和稳定性。传感器安装位置的优化或选取可通过2 种方式进行：1）选取合适的且纵向连续性极好的位置安装传感器；2）建立波浪弯矩间接监测的初始数学模型，得到总传递矩阵，然后由D-最优设计法或C-最优设计法计算得到。前一种方法简单，后一种方法较为复杂。本文以半潜船平行中体横剖面为例，阐述测点优化方法的应用。

半潜船上甲板以下部分几乎全为压载水舱，所以仅有上甲板适合安装传感器。在上甲板的上表面，纵舱壁与上甲板连接处的纵向连续性最佳，其次为纵向骨材与上甲板的连接处。

由D-最优设计法或C-最优设计法计算安装位置的前提是建立初始数学模型，并得到总传递矩阵。

波浪弯矩间接监测的初始数学模型可表示为：

式中：Kn×2为总传递矩阵，表示外力矩向量M2×1与所有候选测点处结构纵向平均应变向量εn×1间的映射关系；M2×1为外力矩或波浪弯矩向量M2×1；εn×1为所有候选测点处结构纵向平均应变向量。

为得到初始数学模型，需首先确定候选测点的位置，即人为确定所有合适的长基线应变仪的安装位置。以半潜船平行中体为例，仅有上甲板上表面适合布置长基线应变仪。半潜船上甲板与纵向骨材或纵舱壁连接处的纵向连续性最佳。故选取这些位置作为候选的传感器安装位置，如图3所示，即1～39点内所有的纵向骨材或纵舱壁与上甲板连接处，共计39个候选测点。

图3 候选的传感器安装位置Fig.3 Candidate sensor locations

假如在39 个候选测点处安装长基线应变仪，则初始数学模型可表示为：

若已知波浪弯矩向量M2×1和所有候选测点处结构纵向平均应变向量ε39×1，总传递矩阵K39×2可表示为：

取波浪入射角为30°时且波高为2 m 的总纵弯矩最大点对应的波浪状态用以总传递矩阵的计算，如图4所示。

图4 总传递矩阵计算工况Fig.4 Load case of calculation of total transfer matrix

波浪入射角为30°时且波高为2 m 时，计算点对应频率下的总纵弯矩和横向弯矩可由AQWA 直接提取，从而得到波浪弯矩向量M2×1。根据波浪入射角为30°、波高为2 m 以及计算点对应频率提取波浪载荷并将其映射到船体湿表面，然后在经典ANSYS中计算结构响应，最后提取所有候选测点处的结构纵向平均应变，即ε39×1。将波浪弯矩向量M2×1和结构纵向平均应变向量ε39×1代入式（8）计算出总传递矩阵K39×2。

计算出总传递矩阵K39×2后，由D-最优设计法或C-最优设计法将总传递矩阵K39×2缩减至K2×2，从而得到最终的传递矩阵以及传感器安装位置。在本算例中，D-和C-最优设计法的计算结果相同，优化的传感器安装位置如图5 所示。

图5 优化的传感器安装位置Fig.5 Optimised sensor locations

3 改进方法在全船有限元仿真中的应用

波浪弯矩间接监测方法的仿真验证包含3 个主要步骤：

1）用AQWA计算波浪载荷；

2）将波浪载荷映射到结构湿表面，用经典AN‐SYS计算结构响应；

3）提取结构响应反求波浪弯矩。

船舶水动力模型如图6 所示，其中入射波方向间隔为30°。

图6 船舶水动力模型Fig.6 Hydrodynamic model of ship

船舶水动力模型的单元总数为33 903，其中湿表面单元数，即水线面以下的单元数为28 907，如图7所示。

图7 船舶水动力网格Fig.7 Hydrodynamic mesh of ship

频域波浪载荷计算时，频率范围为0.02～0.3 Hz，平均内插69个频率点，共计71个频率点。图8所示为波浪入射角为0°，频率为0.084 Hz，相位角为158.2°，波幅为1 m的计算结果。

图8 水动力计算结果Fig.8 Hydrodynamic results

对应某入射波方向、频率、相位角和波高的船体湿表面的波浪面压力可由AQWA-WAVE 模块导出，然后在经典ANSYS 中加载到结构湿表面并计算结构响应。由于水动力模型和结构有限元模型的单元不一致，所以波浪载荷通过映射方式加载，如图9所示。

图9 波浪载荷加载Fig.9 Loading of wave load

改进法的精度验证步骤与传统方法相同，2 种方法的反求结果如图10所示。

图10 改进方法的计算结果Fig.10 Calculation results of improved method

从图10中可以看出，在绝大部分工况下改进方法的反求精度高于传统方法，在极少数工况下改进方法的反求精度略低于传统方法。在横浪情况下，改进方法和传统方法的精度都不高。波浪入射角为0°、30°、150°和180°时，改进方法的反求精度较高。波浪入射角为60°和120°时，改进方法的反求精度次之。

4 某大型半潜船实船实验

为验证改进方法在静水弯矩监测的精度和稳定性，以国内某大型半潜船为测试对象，共计安装4支线性变差动变压器（linear variable differential trans‐former,LVDT）长基线应变仪，其中2 支安装于船中上甲板处，1 支安装于上甲板距离船艏1/4 船长的左舷处，如图11 所示。另1 支安装于上甲板距离船尾1/4 船长的左舷处。此外，船中2 支长基线应变仪的安装位置由C-最优设计法计算得到。长基线应变仪基座焊接于甲板特定位置，并与接线盒与信号调节单元连接。

图11 长基线应变仪安装Fig.11 Arrangement of long base strain gauge

传感器安装完成后，在传感器外部安装保护罩以保护传感器不受外力损坏。结构监测系统只有传感器布置在舱室外，其余部分集中在舱内控制台。

在静水状态对监测系统进行初始化设置，并计入此时结构初始弯矩，初始弯矩由装载计算机直接读出。监测系统设置完成后，某大型海上钢结构逐渐移动至半潜船上甲板。大型海上钢结构移动至半潜船上甲板后，装载计算机会计算出监测横剖面的总纵弯矩（静水弯矩），如图12（a）所示，监测系统计算结果如图12（b）所示。

在本案例中，装载计算机计算得到的船中横剖面总纵弯矩为-124×104kN·m，监测系统得到的总纵弯矩为-119×104kN·m。若以装载计算机的计算结果为基准，则监测系统的总纵弯矩计算结果或改进方法的计算结果精度较高。

结构加载之后，半潜船航行于波浪状态中。监测系统采用低通滤波，截止频率为3 Hz。由于半潜船处于重载状态，结构重心增高，因而船体横稳性下降。所以在整个航行过程中，半潜船刻意避开了高海况，仅选择较为平稳的海域航行。船舯横剖面布置的2支长基线应变仪在60 s内的监测数据如图13所示。

图13 结构响应监测数据Fig.13 Structural response monitoring data

从图13 中可以看出，结构纵向平均应变的监测数据比较平稳，结构纵向平均应变的波动不超过10。由改进方法得到的总纵弯矩如图14所示。

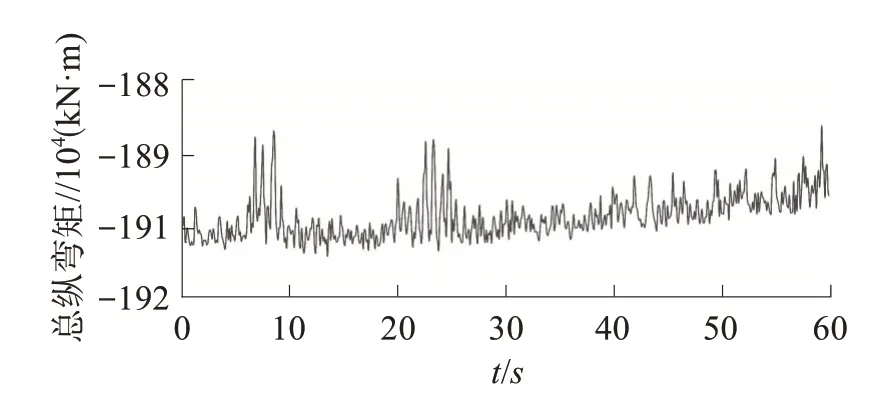
图14 总纵弯矩计算结果Fig.14 Calculation results of vertical bending moment

从图14 中可以看出，监测横剖面的总纵弯矩计算结果比较平稳，其波动不超过20 000 kN·m。但是，在航行状态中，波浪弯矩间接监测改进方法的计算精度无法验证。因为，在航行状态下，船体所承受的波浪弯矩始终未知，即缺少一个验证基准。

5 结论

1）对于非大开口船体梁波浪弯矩的间接监测，本文通过有限元仿真（船体波浪载荷计算、波浪载荷映射加载、船体结构响应以及通过结构响应反求波浪弯矩）验证了传统方法的精度水平。

2）为进一步提高波浪弯矩间接监测的精度，本文引入了C-最优设计法和D-最优设计法优化长基线应变仪的安装位置以提高波浪弯矩反求精度，得到非大开口船体梁波浪弯矩间接监测的改进方法。有限元仿真算例表明改进方法优于传统方法。

3）为验证改进方法的实用效果，对某大型半潜船进行实船监测，其中传感器的安装位置由C-最优设计法计算得出。在装载过程中，监测得到的船体总纵弯矩与装载计算机输出的总纵弯矩极为接近。